考虑机械载荷和热载荷的温室大棚骨架结构轻量化设计
凡健 易振峰 姚兴智 谢锦鹏 谭文超 王昱

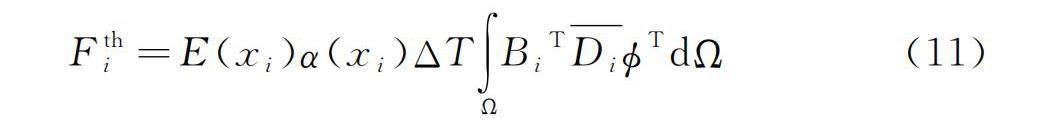
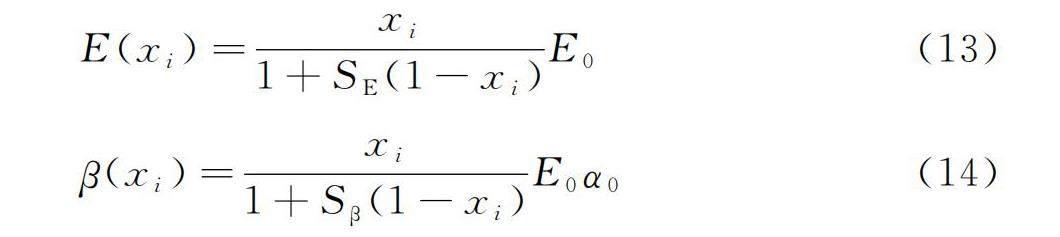
摘要:为探究温度变化对温室大棚骨架结构安全性的影响,建立考虑机械载荷和热载荷的大棚骨架热弹性结构优化设计模型。以机械载荷和热载荷下结构的最大应力值最小化为目标,以结构的总材料用量为约束,考虑机械载荷与热载荷联合作用下的应力分布,实现对大棚骨架的连续体结构优化设计,使结构在满足支撑刚度的前提下最大程度缓和结构的应力集中问题。考虑到热应力优化问题中的设计依赖性和中间变量问题,采用密度过滤函数获得清晰的最优拓扑构型。通过两种典型温室大棚骨架优化算例,对比不同温度变化幅度和不同材料用量下优化结构的最大等效应力,结果表明:该模型在相同体积比下结构最大等效应力优化效率最高可达到约15%,同种载荷条件下体积比增加0.1可实现结构最大等效应力优化效果提高近1%。该研究为考虑机械载荷和热载荷的大棚骨架热弹性结构优化设计提供有效的设计方法,对工程应用中的温室大棚骨架结构设计具有指导意义。
关键词:温室结构;拓扑优化;热弹性结构;应力
中图分类号:S625.1
文献标识码:A
文章编号:2095-5553 (2024) 06-0077-06
收稿日期:2022年10月28日
修回日期:2022年12月15日
*基金项目:国家自然科学基金资助项目(51705161);广州市基础与应用基础研究项目(202102020870)
第一作者:凡健,男,1996年生,安徽滁州人,硕士研究生;研究方向为结构拓扑优化、结构设计。E-mail: fanjian@stu.scau.edu.cn
通讯作者:王昱,女,1987年生,长沙人,博士,副教授;研究方向为结构拓扑优化、轻量化。E-mail: yu-wang@scau.edu.cn
Lightweight design of greenhouse frame structure considering mechanical load and thermal load
Fan Jian1, 2, Yi Zhenfeng1, 2, Yao Xingzhi1, 2, Xie Jinpeng1, Tan Wenchao1, 2, Wang Yu1, 2
(1. College of Engineering, South China Agricultural University, Guangzhou, 510642, China;
2. Key Laboratory of Key Technology on Agricultural Machinery and Equipment, Ministry of Education,
South China Agricultural University, Guangzhou, 510642, China)
Abstract: In order to explore the influence of temperature change on the safety of greenhouse skeleton structure, an optimal design model of greenhouse skeleton thermoelastic structure considering mechanical load and thermal load was established. With the goal of minimizing the maximum stress value of the structure under mechanical load and thermal load, and choosing the total material consumption of the structure as the constraint, the stress distribution under the combined action of mechanical load and thermal load was considered to achieve the optimal design of the continuum structure of the greenhouse framework, so that the structure could minimize the stress concentration of the structure under the premise of meeting the support stiffness. Considering the design dependency and intermediate variables in the thermal stress optimization problem, the density filter function was used to obtain a clear optimal topology. Through two typical greenhouse frame optimization examples, the maximum equivalent stress of the optimized structure under different temperature changes and material consumption was compared. The results showed that the maximum equivalent stress optimization efficiency of the model could reach about 15% under the same volume fraction. Under the same load conditions, increasing the volume ratio by 0.1 could achieve an increase of nearly 1% in the maximum equivalent stress optimization effect of the structure. The obtained conceptual design scheme of the greenhouse skeleton structure has guiding significance for the design of the greenhouse skeleton structure in engineering applications.
Keywords: greenhouse structure; topology optimization; thermoelastic structure; stress
0 引言
温室大棚作为一种作物栽培设施,因其建造和运行成本低,在我国北方迅速发展起来,成为中国设施农业的主体[1]。按照不同的功能需求,可将常见温室大棚分为两大类:连栋温室和日光温室。长期以来,温室结构的有关研究主要集中在温室结构受到各种机械载荷工况下结构的安全性研究[2-4],忽略了昼夜温差变化产生的热应力对大棚结构性能的影响。当热应力的存在使结构内部应力超过许用应力时,则导致结构破坏,给现实农业生产带来安全隐患[5]。
除了在典型温室结构的基础上进行尺寸优化外,拓扑优化作为力学工程领域的先进设计方法[6],近年来发展了一系列的优化模型,被应用于解决土木、车辆、仪器设备等[7-9]工程结构的机械载荷和热载荷作用下的应力问题。桁架结构是温室大棚骨架结构中最为常见的形式,通过拓扑优化方法可合理布置桁架单元的空间分布,可以提升其承载能力[10]。然而,鲜有文献在针对温室大棚骨架结构研究的同时,综合考虑机械载荷和热载荷的结构应力问题。
本文将基于连续体拓扑优化方法,针对设施农业对大棚骨架结构的刚度和热变形以及轻量化的工程需求,建立考虑机械载荷和热载荷作用下结构应力分布的设计模型,在轻量化的同时使得结构具有较高的刚度和较小的热变形。为验证该优化模型的可行性,对两种典型温室大棚骨架优化设计算例,针对常见温室主要承重结构和工作环境特点给出优化设计方案,获得满足实际农业生产需要的结构。
1 考虑机械载荷和热载荷的结构优化模型
1.1 连续体结构拓扑优化方法
当前连续体结构优化领域的主要方法有:尺寸优化、形状优化和拓扑优化。拓扑优化作为一种启发式的结构设计方法,指在满足已知的约束、载荷和边界条件的情况下,通过将所求结构的某种力学性能转化成目标函数,建立其与结构参数的数学模型,进而采用数值优化算法优计算出最优的结构参数,最终获得最优结构的过程。主流的拓扑优化方法可分为以均匀化为主的材料插值类方法[11]和描述结构形状函数类方法,如水平集法[12]。结构的拓扑优化旨在设计区域内寻找一个给定体积的子区域,使得该区域对应的目标函数(如结构柔顺度、结构位移等)取得极值。引入离散变量的材料密度函数,如式(1)所示。
x=1x∈Ωsolid
0x∈Ωvoid(1)
式中: Ωsolid——实体材料域;
Ωvoid——孔洞材料域。
由于整数模型的计算求解非常困难,通常采用变量连续化方法将0~1整数变量问题变为0、1间的连续变量优化模型。上述变量连续化后的模型是一个病态问题,优化解表现为中间密度值、棋盘格和网格依赖性,可采用中间密度惩罚模型和棋盘格控制措施解决上述问题。常用的中间材料惩罚模型有SIMP(Solid Isotropic Material with Penalization Model)[13]和RAMP(Rational Approximation of Material Properties)[14]模型。由于热载荷问题的复杂性,本文的拓扑优化模型基于RAMP模型建立,将在材料插值模型部分详细阐述。
1.2 热弹性结构优化模型
考虑机械载荷和热载荷的的热弹性结构轻量化设计问题,结构变形为机械载荷与热载荷联合作用下的总体变形,以结构的最大应力最小化作为目标函数,以结构的体积比(即总材料用量)为约束,建立相应的热弹性结构优化模型如式(2)所示,示意图见图1。
本文模型采用优化领域广泛应用的渐进优化法MMA(Method of moving asymptotes)[15]进行求解。
minσmax=σpn
s.t.KU=Fm+Fth
V=∑Ni=1xiv0≤V0
0
式中: σmax——结构最大应力;
σpn——结构等效最大应力;
K——总刚度矩阵;
U——总节点位移矩阵;
Fm——作用在结构上的机械载荷;
Fth——变化温度场产生的热载荷;
V——结构优化后的体积;
xi——第i个单元的单元密度;
v0——单元的体积;
V0——给定材料体积上限;
xmin——单元的最小密度值,取0.001以避免总刚度矩阵的奇异;
N——设计变量数目。
2 优化模型的实施
2.1 应力计算
针对基于密度的最大应力最小化结构优化问题,拓扑优化迭代过程中出现的奇异现象存在于基于密度的拓扑优化中,即当单元密度为很低的值时依然存在应变导致局部出现人造大应力的现象。应力松弛方法[16]以减轻低密度单元的应力,可使优化稳定进行。同时,在衡量结构的应力时,只能得到每个单元的局部应力大小,无法建立结构整体应力水平和局部单元应力大小的联系,但考察每一个单元则大大加重了计算成本。因此,使用P范数近似应力最大值[17],将各个单元应力分量整合成一个衡量值,提高计算效率。
对于热弹性结构而言,第i个单元的应力矢量σi如式(3)所示。
σi=D0(BUi-α0ΔT?T)(3)
式中: D0——固体材料的弹性矩阵;
B——应变—位移矩阵;
α0——固体材料的热膨胀系数;
ΔT——结构受到的均匀温升场;
?T——列向量,?=[1 1 0]。
对于二维平面问题,单元应力σi是一个3×1的列向量,不便于优化的开展。采用von·mises应力准则,将σi整合成一个等效应力σvmi。
σvmi=(σi12+σi22+3σi32-σi1σi2)12(4)
式中: σi1、σi2、σi3——σi的三个分量,表示为水平方向应力、竖直方向应力和切应力。
为解决应力奇异问题,这里引入q松弛法对单元等效应力进行惩罚
σvmi=xqiσvmi(5)
式中: q——惩罚因子,这里取0.5。
为了实现目标函数连续可导,采用P范数近似全局最大应力
σpn=∑Ni=1σvmiP1P(6)
式中: P——范数系数,本文P取8。
2.2 材料插值
热弹性结构相对传统只受机械载荷的优化问题更加复杂,因其敏度与设计变量有关,在优化过程中存在符号改变,给优化过程带来不稳定性。传统的SIMP插值方法在表示单元伪密度的设计变量x趋近于0时,其导数为0,这阻碍了热应力敏度符号的转变,影响优化过程的顺利进行。因此,本文引入RAMP插值方法分别惩罚刚度和热应力。
对于第i个单元,其单元刚度矩阵和节点热应力矢量表达如式(7)所示。
Ki=∫ΩBiTDiBidΩ(7)
Fthi=∫ΩBiTDiεthidΩ(8)
式中: Di——密度为xi的单元等效弹性矩阵;
εthi——单元i的热应变矩阵。
Di=E(xi)D0(9)
εthi=α(xi)ΔT?T(10)
式中: E(xi)——材料的插值函数;
α(xi)——单元密度为xi时的等效热膨胀系数。
因此,式(8)可被改写为
Fthi=E(xi)α(xi)ΔT∫ΩBiTDi?TdΩ(11)
其中只有αi和Di与变量xi有关,引入表征材料固有特性的热应力系数(TSC)[18]概念来表达三者关系。
β(xi)=E(xi)α(xi)(12)
根据RAMP插值方法,等效弹性矩阵Di和热应力系数β(xi)可以表达成
E(xi)=xi1+SE(1-xi)E0(13)
β(xi)=xi1+Sβ(1-xi)E0α0(14)
式中: SE——杨氏模量插值系数;
Sβ——TSC插值系数;
E0——固体材料的杨氏模量;
α0——固体材料的热膨胀系数。
SE和Sβ值的选取影响迭代的稳定性,并且当SE<Sβ时迭代产生震荡[19]。根据数值试验经验,这里选取SE=8,Sβ=0。
2.3 密度过滤
基于变密度法的拓扑优化方法是通过将0-1离散变量转化成连续变量,这将导致在优化过程中产生无物理意义的具有中间密度的单元。选用合理的材料插值模型参数,可惩罚中间密度往0-1方向逼近。在产生数学层面上局部最优解的同时,结构的局部区域伴随产生材料密度为0和1周期分布的状态,即棋盘格现象,增加了结构加工成型的难度。针对上述问题以及2.1节提到的应力非线性问题,单元的应力极易受其相邻元素的影响。通过施加密度过滤,可有效防止棋盘格现象并且降低相邻元素对于单元应力的影响,使优化收敛于全局解。
本研究中采用的密度过滤可定义为
x~(k,l)=∑m,nH(m,n)x(k-m,l-n)∑m,nH(m,n)(15)
式中: x(i,j)——第i行第j列的单元密度;
x~(i,j)——第i行第j列单元过滤后的伪密度;
H(m,n)——离散变量m,n的过滤核函数。
H(m,n)=max[0,rmin-δ(m,n)](16)
式中: δ(m,n)——相距m行n列两单元的中心距离;
rmin——最小过滤半径。
rmin的大小影响着过滤后结构细节枝干的数量,同时决定结构的最小尺寸。
3 典型大棚骨架结构轻量化设计
针对实际农业应用领域两种典型温室结构:连栋温室和日光温室,如图2所示,分别选取其主要承重结构作为设计域进行优化。建立两种温室主体框架部分二维模型,以均匀密度场作为初始设计,设定外围轮廓作为非设计域,代入本文的模型进行优化。选择现实生活中常用的Q235钢材作为材料,其杨氏模量E为200GPa,泊松比μ为0.3,热膨胀系数α为1.20×10-5,许用应力为235MPa。
3.1 连栋温室主体承重结构优化
连栋温室主体结构部分如图3所示。该部分为轴对称结构,为减少优化过程的计算量,截取框架右半边作为设计区域。结构长l=800cm,高h=400cm,厚度t取1cm,非设计域(图3中黑色边框)宽度为20cm,整个区域离散成80×40的平面四节点有限单元。结构同时受到均匀温度场ΔT和分布载荷t-作用,分布载荷随着外轮廓倾角的变化呈1000N/m到10N/m渐变。右下方采用固定约束,选择0.3作为体积比。为探究不同温度变化对结构应力的影响,ΔT分别选择0℃、10℃、20℃和50℃,优化后拓扑结构和应力分布见图4,优化结果见表1(表中表达式上标init和opt分别表示初始构型和优化构型),η表示优化效率,计算如式(17)所示。
η=σinitpn-σoptpnσinitpn(17)
由表1可知,当连栋温室结构只受到机械载荷时,优化后的结构与实际农业生产应用的温室结构相似,其应力水平远低于材料的许用应力。加入热载荷后,结构的最大等效应力根据温升大小的变化同幅度的增加,伴随着优化效率的小幅提升。从图4可知,等效最大应力值大于结构实际应力最大值,对于P范数等效最大应力的方法造成的与真实应力的差距,可通过增大范数系数P的值缩小。
此外,升温幅度的不同,结构拓扑也有相应的改变,但始终保持三条棱的样式。温升为10℃时,优化后的结构应力水平在许用应力之下;20℃及以上的温升,结构的最大应力则严重超过了许用应力。研究发现,优化后的结构最大应力出现在右下角支撑区域处,通过对初始框架模型右下角进行局部优化后再进行拓扑优化,可有效降低结构应力集中。
3.2 日光温室主体承重结构优化
日光温室主体框架部分如图5所示。结构长l=800cm,高h=400cm,厚度t取1cm,非设计域宽度为20cm。整个区域同样离散成80×40的平面四节点有限单元。左侧斜坡受到均布载荷800N/m,右侧斜坡受到均布载荷t-为100N/m。为探究不同体积比对优化结果的影响,设定温升ΔT为10℃不变,分别选取体积比等于0.2、0.3、0.4,对应优化后的拓扑结构和应力分布见图6,结果如表2所示。
通过表2可知,在同一温升下,体积比增加0.1,优化后结构的最大等效应力减小了约1%且幅度逐渐变小。因此,在实际农业生产应用中进行优化设计时,应当权衡好应力大小和材料用量的关系,选择最合适的参数组合。
4 结论
本文建立考虑机械载荷和热载荷的大棚骨架热弹性结构优化设计模型,将其应用于温室大棚骨架的轻量化设计,同时探究热载荷对温室大棚骨架的结构应力分布的影响。通过探究不同温升和不同材料用量对优化后结构应力状况的影响。
1) 热载荷的加入大幅提高结构的最大应力:在10℃温升时,结构最大应力小于材料许用应力,设计满足使用要求;温升在20℃及以上时,最大应力超出许用应力,最大应力位置不变指导设计需要对结构初始进行改良。
2) 同等温升条件下,总材料用量增加0.1,结构的最大等效应力减小约1%。因此,在设计时应结合实际条件需要,选择出最佳的结构应力大小和总的材料用量组合。
本文不仅为考虑机械载荷和热载荷的大棚骨架热弹性结构优化设计提供有效的设计方法,还给出具有指导意义的符合工程需求的大棚骨架结构概念设计方案。
参 考 文 献
[1]刘志杰, 郑文刚, 胡清华, 等. 中国日光温室结构优化研究现状及发展趋势[J]. 中国农学通报, 2007(2): 449-453.
Liu Zhijie, Zheng Wengang, Hu Qinghua, et al. Current situation and development on structure optimization of solar greenhouse in China [J]. Chinese Agricultural Science Bulletin, 2007(2): 449-453.
[2]肖林刚, 邹志荣, 吴乐天, 等. 寒冷干旱地区日光温室结构的优化设计[J]. 农学学报, 2014, 4(5): 52-55.
Xiao Lingang, Zou Zhirong, Wu Letian, et al. Structural optimization and design of the sunlight greenhouse in cold and arid Regions [J]. Journal of Agriculture, 2014, 4(5): 52-55.
[3]刘丽霞, 雷法究. 两种典型日光温室结构安全性能分析[J]. 林业机械与木工设备, 2016, 44(11): 18-23.
Liu Lixia, Lei Fajiu. Safety performance analysis of two typical greenhouse structure [J]. Forestry Machinery & Woodworking Equipment, 2016, 44(11): 18-23.
[4]Briassoulis D, Dougka G, Dimakogianni D, et al. Analysis of the collapse of a greenhouse with vaulted roof [J]. Biosystems Engineering, 2016, 151: 495-509.
[5]李世萍, 秦小楠, 马倩, 等. 北京力学会第18届学术年会论文集: 工程应用: 轻钢温室结构温度应力及其对策[C]. 北京: 北京力学会, 2012.
Li Shiping, Qin Xiaonan, Ma Qian, et al. Proceedings of the 18th annual academic conference of beijing mechanics society: Engineering application: Temperature stress of light steel greenhouse structure and its countermeasures [C]. Beijing: Beijing Society of Theoretical and Applied Mechanics, 2012.
[6]Bends?e M, Sigmund O. Topology optimization: Theory, method and applications [M]. New York: Springer-Verlag Berlin Heideberg, 2003.
[7]He Y, Cai K, Zhao Z L, et al. Stochastic approaches to generating diverse and competitive structural designs in topology optimization [J]. Finite Elements in Analysis and Design, 2020, 173: 103399.
[8]Szepessy Z, Zoltan I. Thermal dynamic model of precision wire-wound resistors [J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(5): 930-934.
[9]Mankame N D, Ananthasuresh G K. Topology synthesis of electrothermal compliant mechanisms using line elements [J]. Structural and Multidisciplinary Optimization, 2004, 26(3): 209-218.
[10]Xu L, Min H. Optimum design of cold formed steel residential roof trusses [J]. International Specialty Conference on Cold-Formed Steel Structures, 2000.
[11]Suzuki K, Kikuchi N. A homogenization method for shape and topology optimization [J]. Computer Methods in Applied Mechanics and Engineering, 1991, 93(3): 291-318.
[12]Wang M Y, Wang X, Guo D. A level set method for structural topology optimization [J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(1): 227-246.
[13]Rietz A. Sufficiency of a finite exponent in SIMP (power law) methods [J]. Structural and Multidisciplinary Optimization, 2001, 21(2): 159-163.
[14]Stolpe M, Svanberg K. An alternative interpolation scheme for minimum compliance topology optimization [J]. Structural and Multidisciplinary Optimization, 2001, 22(2): 116-124.
[15]Svanberg K. The method of moving asymptotes-a new method for structural optimization [J]. International Journal for Numerical Methods in Engineering, 1987, 24(2): 359-373.
[16]Cheng G D, Guo X. ε-relaxed approach in structural topology optimization [J]. Structural optimization, 1997, 13(4): 258-266.
[17]Duysinx P, Bends?e M P. Topology optimization of continuum structures with local stress constraints [J]. International Journal for Numerical Methods in Engineering, 1998, 43(8): 1453-1478.
[18]Deaton J D, Grandhi R V. Stiffening of restrained thermal structures via topology optimization [J]. Structural and Multidisciplinary Optimization, 2013, 48(4): 731-745.
[19]Gao T, Zhang W. Topology optimization involving thermo-elastic stress loads [J]. Structural and Multidisciplinary Optimization, 2010, 42(5): 725-738.

