人文视角下的城市道路规划与交通拥堵治理

收稿日期：2024-03-07

作者简介：房雨宵（2002—），男，本科，研究方向：交通运输。

摘要 随着城市化的快速发展，城市交通拥堵问题日益突出，如何进行科学合理的道路规划和有效治理交通拥堵成为城市发展的重要课题。文章以青岛市市南区为例，从人文视角出发，研究了城市道路规划与交通拥堵治理的关系。通过对城市交通发展历程和现状的分析，揭示了影响交通拥堵现象的内源本质。在保留原有道路的基础上，提出了一种新的规划方案，并利用MATLAB对其进行模拟仿真实验。通过以人为本的视角探讨城市道路规划和交通拥堵治理的关系，为解决城市交通拥堵问题提供了新的思路和方法。

关键词 城市交通；道路规划；交通拥堵；交通流量

中图分类号 D631.5文献标识码 A文章编号 2096-8949（2024）11-0033-04

0 引言

城市是一个大型的人类聚居地。随着城市化进程的加速，城市交通拥堵问题日益突出。人们对于城市道路规划、交通治理的关注与需求愈发迫切。青岛市市南区作为繁华地段，交通拥堵问题备受关注。该文将从人文视角出发，分析其交通拥堵成因，探讨青岛市市南区的道路规划与交通拥堵治理，并给出优化调整解决方案，旨在为解决城市交通难题提供新思路与策略。

1 城市交通拥堵研究现状

随着城市化的快速推进，在人口数量不断增加、土地资源总量不变的情况下，城市发展出现了土地利用需求大于供给的现象，一系列“城市病”随之出现。在城市交通方面最显著的表现为道路拥堵问题的日益严重。为切实缓解城市道路拥堵问题，韦敬楠[1]从道路交通供需平衡视角入手，以城市道路交通需求指标为参数，将城市拥堵划分为轻度失衡、中度失衡、重度失衡三类。张可可[2]等提出基于评价—预测—判定—管控的全过程模型。选取流量、速度和时间延误三个参数，制定了交通运行状态综合评价体系。徐淑贤[3]等从城市空间布局入手，综合分析城市区块职能，以推动城市空间布局均衡化作为缓解交通拥堵的方法。刘婕[4]等基于国内拥堵较为严重的城市及其目前的治理方案，以调控出行需求与提高路网承载能力作为改良方向。

2 国内外常见城市道路网结构

影响城市道路网结构的因素分为自然因素和社会因素。自然因素有地形地势、气候、河流等；社会因素涉及经济、社会、文化等。不同城市间的自然和社会因素均存在着一定的差异，这些差异使得各地的城市道路网结构存在着一定的不同，形成了各自的风格。

通过对国内外常见城市道路网的分析，可以得到以下结论：

（1）道路网的形成是一个长期过程，但一经确定就很难大幅度地改变。

一个城市道路网的形成过程是与城市发展同步的，道路网的建设是百年大计，其在主要道路完工后，后续建设基本多为在此基础上的增添与改良，基本不会出现大幅改变。即使遭遇毁灭性的破坏，其重建也多以原先道路网为模本。

（2）地区文化等人文因素是道路网结构形成的影响因素之一。

地区间人文因素的差异，在一定程度上会影响其路网的整体布局。

（3）相同情况下，方格状道路网与放射状道路网互有利弊。

土地利用率层面，在同样的面积内，方格状道路网由于其所划分出来的是较为规整的四边形或多边形区域，可供进行区域内建筑物修建的面积较大；放射状道路网划分出的是不规则的区域，存在过窄等不适合进行建设的土地，整体上方格状道路网土地利用率高于放射状道路网。

通行效率层面，相同的起点与终点，放射状道路网是直接的点对点的线段式连接，而方格状道路网是基于第三点或更多的点并以其为中间点进行两段式或多段式的连接。在单纯的空间几何路程上，放射状道路网明显优于方格状道路网，同时，方格状道路网在交叉路口处还会出现等候交通信号灯乃至交通拥堵等情况，进一步降低了其通行效率。

3 市南区交通现状及其存在问题的解决方案

3.1 市南区交通现状

市南区作为青岛老城区，与其他城市老城区相似，存在着较为严重的交通拥堵问题。受自然地形的限制，市南区中西部老城区的路网采用自由式布局方式，道路相对狭窄，宽度一般为12～20 m。根据调查，区内现有道路242条，道路长度为106.28 km，路网密度为8.85 km/km2。由于区内地形坡度较大，道路纵坡较高，故畸形路口较多。

截至目前，青岛市机动车保有量约365.4万辆，其中多为家用汽车，总体上机动车保有量仍以较快速度在增长。同时，由于青岛作为旅游城市，存在大量外地来青车辆，因此，青岛的机动车输入源可视作无限大，随着旅游业的逐步复苏，此情况对市南区道路网存在潜在冲击。对市南区较为老旧的道路网存在着较大的压力。

3.2 现行已有解决方案的局限性

根据《市南区城市更新专项规划》，青岛关于交通方面的城市更新实施策略可概括为“交通引领发展，建设步行友好城区”。

目前市南区的规划方案，未来将会在较为完好地保留原有城区风貌的情况下，采取现代化的交通系统以期满足日益增大的交通压力，在原有的基础上融合新的交通方式，继而实现“旧路新貌”。该建设工程可视作老城区保护性改造的典型案例。

目前我国城市对老城区道路网改造的通行方法有两种：拓宽原有道路和增加公共交通。

从拓宽原有道路方法的角度来看，由于市南区的建成历史较早，其道路周边分布大量历史文物古迹建筑，为道路拓宽预留空间较少。同时大型施工设备施工时产生的振动会对周边文物建筑产生不可逆的损坏[5]。该方法只可在市南区部分地段施行，大规模推广难度较大，不具备普适价值。

增加公共交通方面，市南区的公共交通目前仍以道路公交为主。但由于其道路流量限额，单纯增加公交线路以及发车密度，只会增加其交通拥堵问题。目前市南区公交运行效率亟待提升。由于先前公共交通主要依赖公交，导致出现线路多、流量大，线路重复系数较高等问题，出现车道容量已近饱和，公交车与其他车辆“抢道”的情况。以香港路为例，其高峰时段平均运营速度仅12.8 km/h，受通道宽度制约，公交车辆难以超车，公交“列车化”现象严重，运输效率低下。

以广西路青岛站段为例，该路段交通流源包含青岛站进出客流源、栈桥景区客流源、地铁青岛站客流源、铁路青岛站广西路②公交站源。人流量、车流量均存在较不规则的高峰期。整体上存在较大的交通拥堵隐患。

为缓解周边道路交通压力。目前该路段车道划分为采取上行单车道，为公交专用道，下行三车道，均为公交与社会车辆混用道，其中最右侧车道同时为铁路青岛站广西路②公交站停车道。

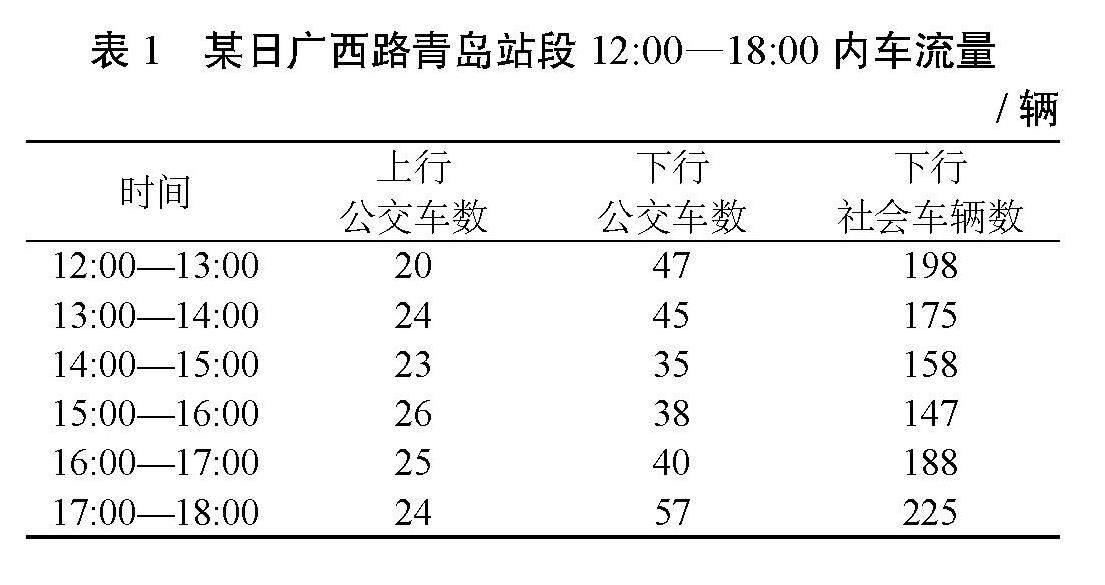
如表1所示，为某日该路段12：00—18：00内车流量统计。

表1 某日广西路青岛站段12：00—18：00内车流量

/辆

时间 上行

公交车数 下行

公交车数 下行

社会车辆数

12：00—13：00 20 47 198

13：00—14：00 24 45 175

14：00—15：00 23 35 158

15：00—16：00 26 38 147

16：00—17：00 25 40 188

17：00—18：00 24 57 225

据表1可知，由于公交车定时发车，不同时间段内上下行公交车数变化幅度较小，但社会车辆数变化幅度较大。结合区位分析可知该路段车辆多为通勤车辆，变化幅度与时间有较大的关联。

3.3 优化调整解决方案

关于市南区交通拥堵的问题，在综合考虑可行性与预期效果的情况下，该文给出的建议如下：

（1）依据“窄马路、密路网”的城市道路布局理念，合理利用城市交通信号控制系统对原有道路网进行二次规划。

“窄马路、密路网”所构建的是一种街区小型化、集约化的城市布局。城市交通信号控制系统采用合理的交通信号配时可以减少车辆停车等待次数，降低车辆延误，缩短旅行时间，而合理的信号配时则会起到反作用，导致时间浪费和能源的额外消耗[6]。二次规划是充分利用现有的道路网，采取道路“再设计”，辅以健全的交通管理系统，优化交通信号[7]，从而提高交通管理运行效率和水平的方法，以期缓解交通拥堵问题。

市南区原有道路网在早期建设中便设立了诸多的中心点。在对市南区道路的二次规划中可充分利用这些原有的中心点，将其再次视作街区的中心，周边道路则构成该街区的道路网。最终将市南区原有的道路网分割成多个“小路网”，各“小路网”共同构成“大路网”，做到路网的区划式管理。

（2）提升交通运作的智能化水平，提高动态自适应调整能力，车道“潮汐化”变动。

包括青岛在内，绝大部分城市的交通信号仍采用较为原始的被动响应式控制。传统信号控制系统都只是关注控制方法和控制策略的优化，而对于交通状态参数变化并没有充分考虑。[8]在交通信号方面使用自适应控制方式，可实现路段运行的动态化、灵活化调整，以提升路网整体的运行效率。

在公交运行方面，目前主要存在公交“列车化”现象，公交系统投入运力与时段需求、道路压力不匹配。引入自适应控制系统后，可通过系统所反馈依据的实时情况，依据各时段需求灵活调配车辆，动态调整发车间隔。必要时可采取“甩站”等措施减少车辆停站时间，提升公交系统整体运行效率。

在车道方向上，可根据节点路段的实际情况，灵活调整各支路行驶方向以及支路内各车道的行驶方向。实现道路方向的“潮汐化”动态调整。

3.4 可行性论证

对于所提出的建议，将市南区的道路网简化为网络模型，就目标问题视作最短路和最大流问题，运用Dijkstra算法和Ford-Fulkerson标号算法进行可行性论证。

狄克斯特拉算法（Dijkstra）是由荷兰计算机科学家狄克斯特拉于1959年提出的，是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题[9]。

最短路径问题的线性规划数学模型为：

（1）

式中，xij——选择弧（i， j）的状态变量，选择弧（i， j）时xij=1，不选择弧（i， j）时xij=0；cij——弧（i， j）的距离，得到最短路问题的网络模型。

Ford-Fulkerson算法（FFA）是一种贪婪算法，用于计算流网络中的最大流量。由L. R. Ford， Jr。和D. R. Fulkerson于1956年出版[10]。

最大流问题的线性规划数学模型为：

（2）

式中，cij——弧（i， j）的容量； fij——弧（i， j）的流量。容量是弧（i， j）单位时间内的最大通过能力，流量是弧（i， j）单位时间内的实际通过量。fmm～fkm——弧中反向流计算时减去。fim——中间点输入量；fmj——中间点输出量，中间点输入量和与输出量和应相同。

将A视作起点，F为终点，A至F有着多条路径可供选择。从A开始，依次代入各路段的路长cij与流量fij。经迭代计算后，在去除其他客观因素的前提下，该道路网络最短路径为A—E—F，最短路径为min Z=8，最大流为max v=16。

假设在不考虑其他客观因素的影响下，E至F方向在某一时段T区间内流量趋于饱和，存在拥堵问题，F至C1至A方向区间流量较少。引入自适应控制方式后，采取临时交通管控，将E—F段设置为单行道，只允许F至E方向行驶，E—F段更新为F至E单向弧；将C1—F段设置为单行道，只允许C1至F方向行驶，C1—F段更新为C1至A单向弧。设置完成后其网络模型图如图1与图2所示，相应道路路长不变，容量变为原有两倍。

图1 网络模型图路长F 图2 网络模型图容量 D

运用最短路问题Dijkstra算法和最大流问题Ford-Fulkerson标号算法可得到，该情况下最短路径为A—C1—F和A—C2—F，最短路径为10，最大流为21。

从该理想化模型可知，该路段最大流与最短路径仅与A—E—F段和A—C1/C2—F段有关。设A—E段长度与允许流量为a，E—C2段长度与允许流量为b，得理想最短路径与最大流变化率函数。

采用MATLAB进行仿真实验分析，得出关于上述两个网络图数学模型的图像，同时随机生成20组（a，b）正数组，带入两个模型进行验证，如图3～4所示，其运算结果如表2所示。

综上，在?F及最短路径增加率较小的情况下，?D及最大流量可获得较大增加。模拟实验结果符合预期要求。

图3 ΔD函数图像

图4 ΔF函数图像

表2 函数随机运算结果

序号 ?F ?D 序号 ?F ?D

1

2

3

4

5

6

7

8

9

10 0.358 2

0.499 6

0.490 1

0.114 1

0.266 5

0.345 4

0.496 9

0.384 7

0.394 1

0.492 2 0.114 1

0.265 5

0.214 1

0.228 6

0.294 9

0.321 1

0.278 7

0.296 3

0.235 0

0.321 1 11

12

13

14

15

16

17

18

19

20 0.194 9

0.499 7

0.479 5

0.197 7

0.944 6

0.570 9

0.442 7

0.496 3

0.850 9

0.499 8 0.071 6

0.278 7

0.337 5

0.071 6

0.696 3

0.452 6

0.131 5

0.293 8

0.623 8

0.423 8

4 总结

基于“窄马路、密路网”的布局理念，该文提出了一个交通疏导方案——尽可能保留城市原貌。这种混合型道路网结合了方格状和放射状道路网的特点，为未来的城市道路网设计提供了新思路。能够更好地协调“人”与“地”之间的矛盾，最大限度地缓解交通拥堵问题。在未来的城市交通规划和改良中，应更多考虑设计成果对社会环境和自然环境的影响，并以人们对美好生活的需求为出发点，利用现状和历史的数据和经验，通过合理的设计和优化，实现人文和自然的有机融合，逐步解决由于人地矛盾而产生的问题，最终实现城市交通、经济和环境的可持续发展。

参考文献

[1]韦敬楠. 我国城市交通拥堵程度及影响因素分析——基于道路交通供需平衡的视角[J]. 辽宁工业大学学报（社会科学版）， 2023（2）： 36-40.

[2]张可可， 韩春阳， 周京， 等. 精准管控下的城市交通拥堵状态研判与建模[J]. 交通科学与工程， 2022（3）： 113-120.

[3]徐淑贤， 刘天亮， 王婷， 等. 空间一般均衡视角下的城市交通管理研究：现状与趋势[J]. 交通运输系统工程与信息， 2023（3）： 6-19.

[4]刘婕， 聂祥波. 我国部分城市交通拥堵治理现状研究及对策分析[J]. 时代汽车， 2023（13）： 181-183.

[5]张智林. 简析老城区道路改造工程的交通微循环实践思考——以漳州市大同路、大通北路改造为例[J]. 福建建材， 2020（2）： 23-24.

[6]申亮. 交通信号控制自适应模型及相位同步方法研究[D]. 大连：大连理工大学， 2013.

[7]李凤坤， 张永. 基于交通流量自适应控制的路口子系统[J]. 计算机系统应用， 2021（12）： 109-115.

[8]袁二明， 李莹， 李彪. 基于交通拥堵预测的交通网络最短路问题的研究[J]. 中国管理学， 2013（S1）： 43-45.

[9]刘小玲， 李辉， 郭治国. 基于狄克斯特拉算法的车间动态生产能力评估与实现[J]. 微计算机信息， 2006（12）： 96-98.

[10]Backman S， Huynh T. Transfinite Ford-Fulkerson on a Finite Network[J]. Computer Science， 2015.