Π型叠合梁斜拉桥涡激振动性能及气动措施研究

蒋尚君 朱金 鲁胜龙 李永乐 康锐

摘要： Π型叠合梁为气动钝体结构，容易发生气动失稳。本文以一座Π型截面叠合梁斜拉桥作为工程背景，采用风洞节段模型试验与计算流体动力学（CFD）方法，对主梁的涡激振动性能及相应的气动抑振措施展开了研究。在风洞节段模型试验中获得涡激振动风速区间，讨论了不同气动措施的抑振效果，运用计算流体动力学（CFD）方法对主梁涡振发生机理及气动措施抑振机理进行了初步研究。结果表明：在原始断面下，由于尾迹区旋涡的周期性脱落以及主梁上、下表面旋涡演变的相互作用，导致了涡激振动发生。在采取三种不同抑振措施后，除采用上L型导流板断面在+3°风攻角下发生扭转涡振外，其余优化断面均能使得来流平稳地通过，从而抑制涡振发生。本研究可对Π型叠合梁断面的斜拉桥抗风设计提供一定参考。

关键词： 涡激振动； 抑振措施； 叠合梁； 风洞试验； 计算流体动力学（CFD）

中图分类号： O32； U448.27    文献标志码： A    文章编号： 1004-4523（2024）05-0830-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.05.011

引 言

随着经济和社会的发展以及中国高速公路网建设的快速完善，斜拉桥成为跨越山谷、河流、湖泊的主要桥型之一。然而随着桥梁跨径的增加，主梁的自重对桥梁的影响增大［1］。Π型叠合梁通常是中等跨度桥梁中最常见的主梁类型之一。Π型叠合梁采用钢梁和混凝土桥面板相结合的方式，具有自重轻、施工吊装方便、受力性能优越等诸多优点。然而，由于叠合梁具有较钝的气动外形，空气流经梁底时会形成复杂的绕流，使得采用此类断面类型主梁的桥梁容易发生涡激振动现象。因此，需要采取一系列的气动优化措施，确保叠合梁能够更好地应用于桥梁设计中。

目前针对叠合梁断面的涡激振动性能以及抑制措施已有诸多研究。张天翼等［2］研究了风嘴、中央稳定板、裙板、封闭栏杆、内侧隔流板、下导流板等常见气动措施对叠合梁断面涡激振动性能的影响。贺耀北等［3］开展了导流板、稳定板、风嘴、栏杆透风率等单一和组合气动措施对主梁涡振性能的优化研究。Bai等［4］研究了断面外形对主梁涡振性能的影响规律，发现对于长宽比在9.05～11.96范围内的Π型截面模型，增加长宽比会提高竖向和扭转涡振的起振风速。李永乐等［5］通过节段模型风洞试验发现优化检修车轨道位置和在主梁风嘴处设置分流板能有效抑制主梁涡振。段青松等［6］研究了不同阻尼比下主梁的涡振性能，结果表明，主梁的竖向涡振和扭转涡振振幅均随阻尼比的增大而减小，增大阻尼比可以有效抑制主梁的涡振。董锐等［7］研究气动外形对Π型主梁涡振的影响，发现在主梁断面上增设导流板可以有效地降低涡振振幅。钱国伟等［8］研究多种气动控制措施的涡振控制效果，发现在桥梁断面底部双主肋转角处设置水平隔流板能有效减小甚至消除涡激振动，并且水平隔流板越宽对涡振的控制越有效。谭彪等［9］通过研究间距比对叠合梁双幅桥涡振性能的影响，发现最不利间距比为L/D=2～4（L为双幅桥面横向间距，D为梁宽），此时桥面涡振振幅最大且风速锁定区间更长。张志田等［10］研究发现将中央两道防撞栏设计成不透风，中央防撞栏形成上稳定板，主梁下设三道下稳定板，能够有效抑制开口截面桥梁的涡激振动。

由以上文献可知，大跨桥梁涡振方面的研究已经比较丰富，但目前针对Π型叠合梁这一断面形式的涡振机理研究还较为有限，相应的减振措施研究还不够深入。因此，本文以兰原高速东坝头黄河大桥为工程背景，通过节段模型风洞试验与计算流体动力学的方法，对涡振发生机理及气动措施抑振机理进行了初步研究。

1 工程概况及试验参数

1.1 工程概况

兰原高速东坝头黄河大桥是兰考至原阳高速公路兰考至封丘段项目的控制性工点。该桥为三塔四跨钢混叠合梁斜拉桥，跨径布置为140+2×360+140 m，主桥长度为1000 m。主梁采用Π型叠合梁。其“工”字型钢纵梁、小纵梁、横梁通过节点板及高强螺栓连接形成钢构架，桥面板采用预制板，两者通过剪力钉形成整体［1］。桥面最大宽度为38.0 m，钢主梁高度为3.0 m。主梁在吊点处的横断面布置如图1所示。

1.2 试验参数

试验在西南交通大学XNJD?1工业风洞第二试验段中进行，试验段截面尺寸为2.4 m（宽）×2.0 m（高）×16.0 m（长），可调节风速范围为1～45 m/s，并且该试验段设有专门进行桥梁节段模型动力试验的装置。模型由8根拉伸弹簧悬挂在支架上，形成可竖向运动和绕模型轴线转动的二自由度振动系统。试验支架置于洞壁外，以免干扰流场。主梁节段模型采用1∶50的几何缩尺比，模型长L=2.095 m，宽B=0.76 m，高H=0.08 m，模型用PVC塑胶板制作，表1为节段模型的主要参数。

由于本桥采用了三塔双主跨的布置形式，竖弯基频与扭转基频有4种振型组合方式，具体的各振型频率及临界风速如表2所示。为了确定该试验应采用的最不利模态组合，采用《公路桥梁抗风设计规范》［11］中的平板颤振临界风速的计算公式计算颤振临界风速。结果表明：单跨正对称双跨反对称的竖弯（扭转）组合模态的颤振临界风速最低，因此本研究偏安全地选取该模态进行节段模型动力试验。

2 原始断面涡振性能

涡激振动试验在均匀流场中进行，分别在0°与±3°三种来流风攻角下测试了主梁的竖弯以及扭转涡振。已有的研究表明，涡激振动的振幅和锁定风速区间与结构阻尼比联系密切［6］。因此，针对原始断面分别进行小阻尼比和规范规定阻尼比的涡振性能试验，本研究综合采用常用的橡皮筋法和油箱法实现不同阻尼比下的涡激振动试验。根据《公路桥梁抗风设计规范》［11］，钢混叠合梁桥的阻尼比为1%。

为了便于观察涡振现象和确定涡振锁定风速区间，首先进行小阻尼比涡振试验（竖弯阻尼比为0.582%，扭转阻尼比为0.168%）。图2分别给出了三种来流风攻角下的主梁竖弯涡振及扭转涡振响应，图中的风速与振幅均已换算至实桥。试验结果表明：原始断面在小阻尼比涡振试验条件下，三个风攻角下均出现了不同程度的涡激共振现象。其中竖弯涡振最大振幅达到了320.5 mm，发生在+3°风攻角工况，扭转涡振最大振幅达到了1.141°，发生在 +3°风攻角工况下，均超出了规范限值。根据《公路桥梁抗风设计规范》［11］规定，竖弯涡振和扭转涡振的限值分别为h=192.0 mm，θ=0.198°。

接着开展了规范规定阻尼比（竖弯阻尼比为0.906%，扭转阻尼比为0.907%）的涡振试验。图3分别给出了三个风攻角下主梁竖弯涡振及扭转涡振响应。由图3可知：竖弯涡振最大振幅为154.8 mm，发生在+3°风攻角工况，扭转涡振最大振幅为0.110°，发生在0°风攻角工况，均未超出规范限值。

通过对比小阻尼比与规范规定阻尼比试验结果发现，提高阻尼比后，竖弯以及扭转涡振振幅明显下降。此外，虽然规范规定阻尼比下主梁的竖弯涡振振幅以及扭转涡振振幅均在规范限值之下，但是幅值较大，与规范规定值相接近。考虑到桥上行车人员的安全性以及舒适性，需要对原始断面进行气动优化。

3 主梁涡振抑振措施研究

目前，控制主梁涡激振动的方法主要有气动措施、结构措施和机械措施，其中气动控制措施是当前最常用的抑振方法。气动措施可通过改变“桥梁?流场的耦合共振体系”从根本上消除桥梁风振的诱因，其抑振思路较结构措施和机械措施更为主动积极，控制效果也更为明显，控制成本和代价更小［12］。Π型主梁断面属于典型的钝体断面，此类断面的涡振控制应当以改变主梁下部流场为主，因此本文提出上L型导流板、风嘴以及风嘴加水平导流板这三种气动措施对主梁断面进行优化。

3.1 上L型导流板

主梁涡振的控制效果与L型导流板的宽度与高度密切相关。已有研究表明，当L型导流板宽度取2/3主梁高度，高度取1/2主梁高度时，可以保证良好的抑振效果，同时降低造价成本［4］。

因此，本文的L型导流板方案采用上述最优尺寸，即高度为1.5 m，宽度为2 m。L型导流板左右对称地布置（倒置）在主梁的纵梁上翼缘处，具体参数以及布置位置如图4所示。由图5可知，在该优化措施下，-3°，0°风攻角未发生涡振现象；但在+3°风攻角下，发生了扭转涡振，最大振幅为0.081°（限值为0.198°）。

3.2 风 嘴

风嘴是目前在桥梁上应用最广泛的抑振措施之一。战庆亮等［13］发现增设风嘴可以有效抑制开口断面的涡振，增加风嘴结构尺寸后抑振效果更加明显。黄林等［14］发现三角形风嘴可降低主梁断面的竖弯涡振振幅，但对降低主梁的扭转涡振振幅作用有限。孟晓亮等［15］针对风嘴角度较尖、较钝两种状态进行风洞试验，发现较尖的风嘴更加有利于抑制涡振。与上述研究结论不同，赵林等［12］发现较尖的风嘴存在恶化颤振性能的可能性。因此，在采用风嘴作为气动措施时，需对风嘴的尺寸进行研究。

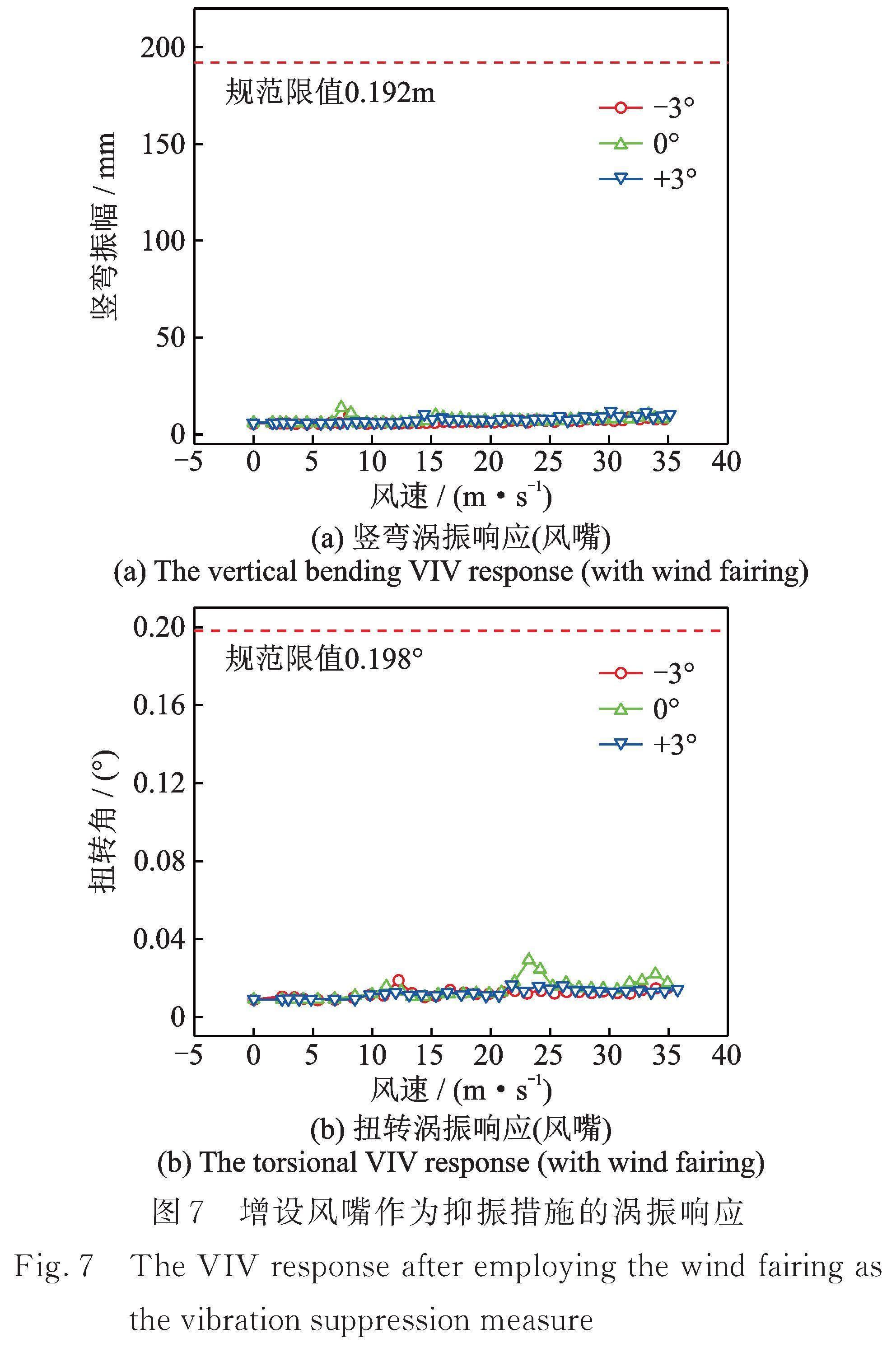
本试验选取夹角为45°的风嘴对称布置在主梁两边，具体参数以及布置如图6所示，试验结果如图7所示。通过观察图7可知：在三个风攻角下均未发生涡振现象。

3.3 风嘴加水平导流板

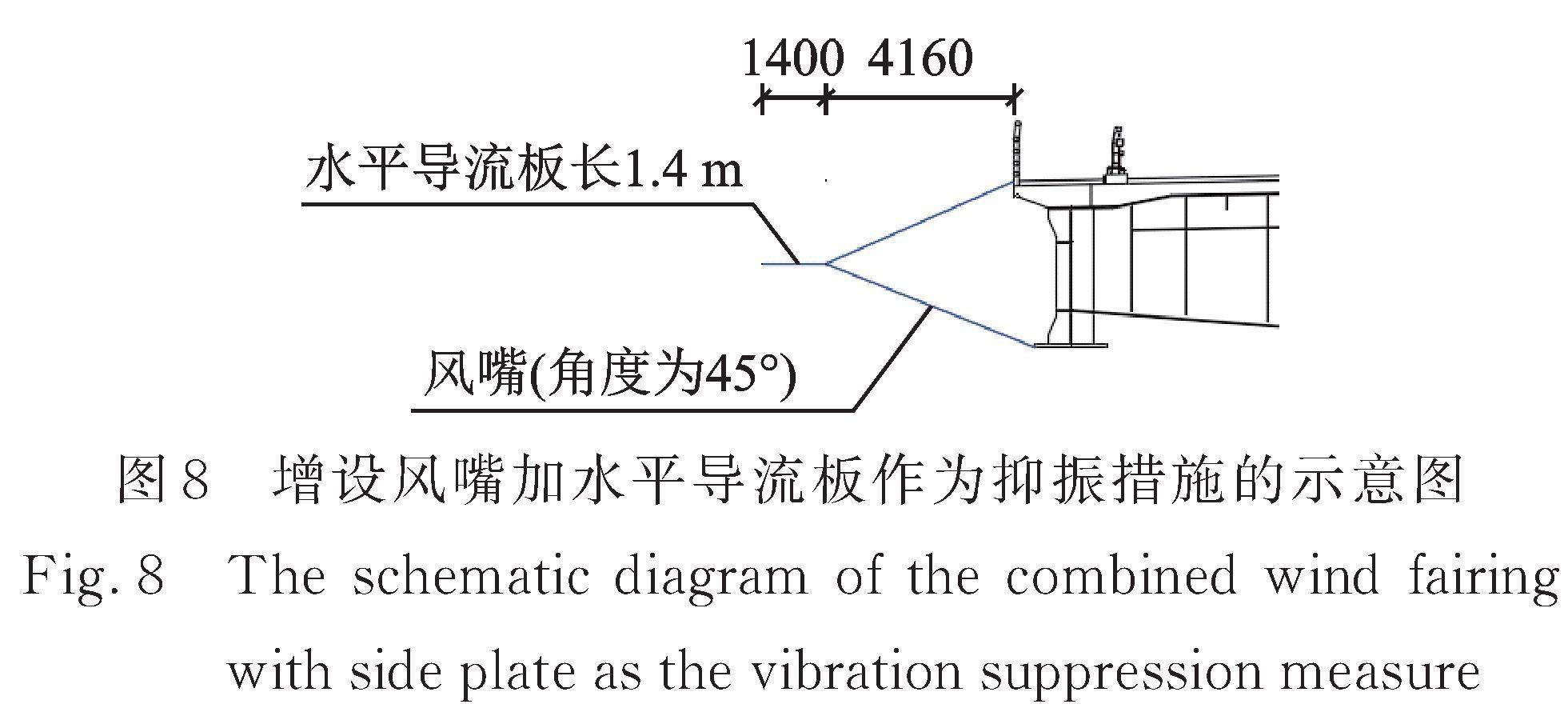
风嘴加导流板也被称作为分流板，风嘴处的导流板的作用在于增加主梁的宽度，从而增加主梁断面的宽高比，让主梁断面更加趋近于流线型。当来流风吹向主梁时，能够使其平滑地吹过主梁，减少流动分离，从而提高结构的气动稳定性［16］。

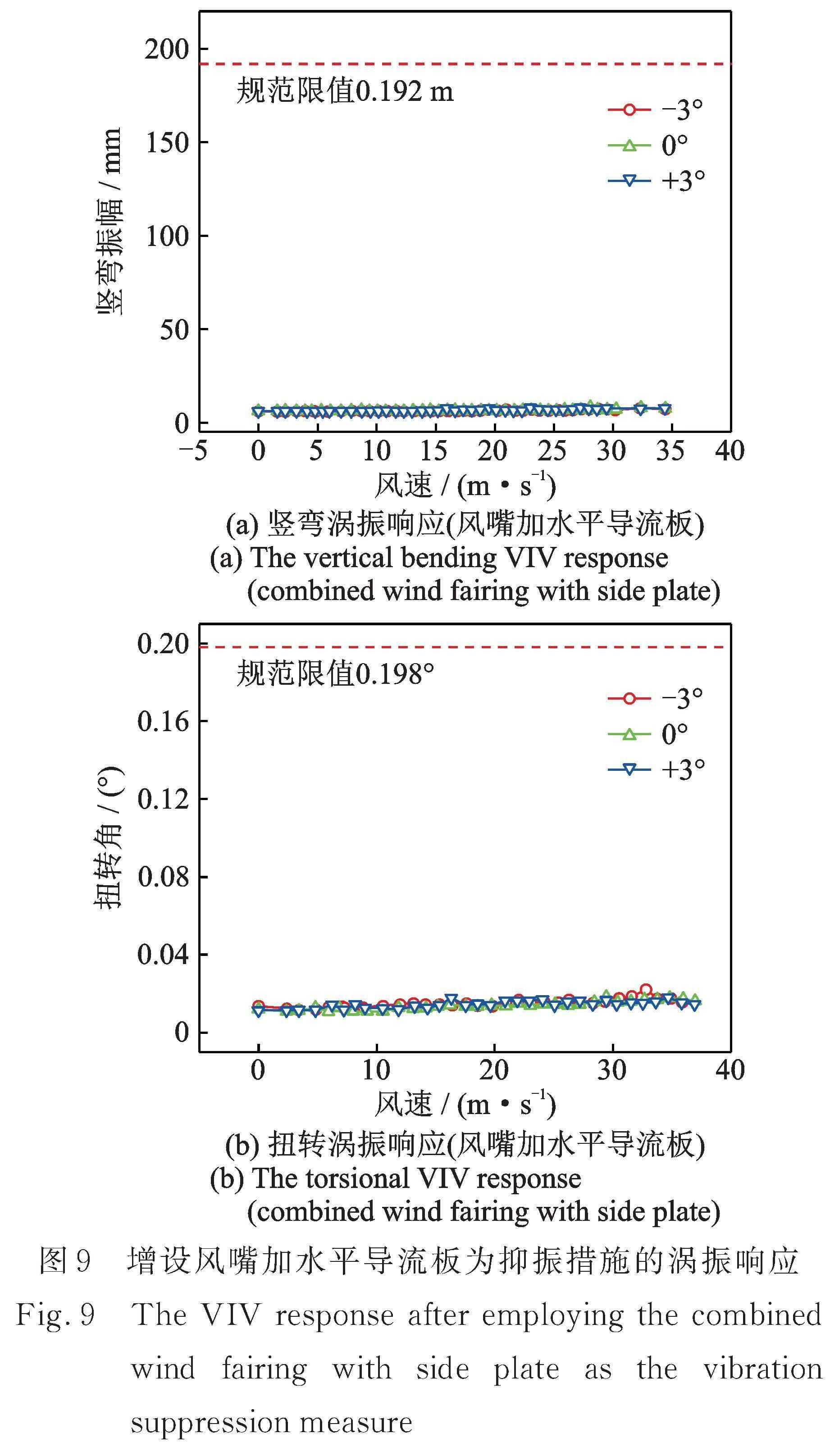
该优化措施是在上述风嘴措施的基础上，增设宽度为1.4 m的水平导流板，并对称布置于主梁断面的两侧，如图8所示。由图9可知：在三个风攻角下均未发生涡振现象，表明该方案能抑制涡振，显著改善主梁的气动性能。

3.4 优化措施小结

主梁气动优化措施试验共完成了9个试验工况，所有试验工况均在规范规定阻尼比条件下进行。试验结果表明：增设上L型导流板后，主梁在+3°风攻角下发生扭转涡振现象；与上L型导流板方案相比，增设风嘴或风嘴加水平导流板后，三个风攻角下均未发生明显涡振响应。综上所述，增设风嘴或风嘴加水平导流板能抑制涡振，显著改善主梁的气动性能。若实桥采用风嘴或风嘴加水平导流板措施，经济成本会相对较高。而采用上L型导流板虽然不能完全抑制涡振，但能将涡振振幅降低至合理水平，是更为经济适用的气动优化措施。

4 数值模拟

4.1 数值模拟参数设定

为了深入研究黄河大桥Π型叠合梁的涡激振动机理，本文采用计算流体动力学数值模拟软件Fluent，分别对原始断面以及三种优化断面的非定常绕流进行了仿真模拟。

CFD二维数值模型采用与风洞试验相同的缩尺模型，宽度B为760 mm，高度H为80 mm，忽略Π型叠合梁的加劲肋、横梁腹板以及横梁加劲肋等横向构件。由于人行栏杆、防撞栏、检修轨道等附属设施对主梁涡振性能影响非常大，因此本文在模拟过程中尽可能按照设计图纸准确地进行模拟，并采用等透风率方法来对其进行简化设计。计算域采用矩形结构，如图10所示。为避免计算域内气体回流及阻塞比对结果造成影响，各边界应离主梁足够远，因此计算域总尺寸取10B×25B，阻塞率小于2%，满足计算要求。计算区域由内至外分别采用结构化网格、非结构化网格以及结构化网格。为了能够使模拟能够更为准确，第一层网格厚度设置为3×10-5 m，各断面的y+值均在1以下。

计算采用SST k?ω湍流模型，压力?速度耦合问题采用SIMPLEC算法求解，压力场和动量方程均采用二阶格式离散，收敛项残差控制为1×10-6。此外，时间步长取0.001 s，入口边界和出口边界湍流强度均设置为0.5%，湍流黏性比均设置为2。为验证网格无关性，本文建立了网格总数32万、53万以及80万三种网格质量的模型，计算结果如图11所示。可以看出三分力系数误差随着网格数的增加而减小，因此为了使模拟能够更为准确，选取了网格总数为80万的模型进行模拟。在模拟过程中，通过保存每个时间步长内的相应数据来获得三分力系数时程。限于篇幅，本文仅给出原始断面在0°风攻角下的升力系数时程曲线，如图12所示，数值模拟相应工况的St数如表3所示。

4.2 原始断面涡振诱因

由表3可知，不同风攻角下原始断面试验的St数与数值模拟的St数相比，误差均在5%以内。由此可以推断，本次模拟能够较好地模拟主梁周围的旋涡脱落。

作用在桥梁上的气动力，主要依赖于循环区旋

4.3 优化措施抑振机理探讨

由前文试验结果可知，在主梁两侧安装风嘴加水平导流板后，主梁在三个风攻角下均未发生涡振。由于篇幅有限，本文仅针对该优化断面下0°风攻角的流线图进行阐述。由图14可知，与原始断面相比，气体绕流特性以及旋涡形状已明显改变。该优化方案没有上表面附着的两个旋涡，主梁下表面的大旋涡尺度明显减小，形成了四个小规模稳定旋涡。同时，与原始断面不同，尾迹区形成了一个稳定旋涡，在整个周期内没有发生周期性脱落现象。该方案显著改变了截面的流线形状，使得来流能够更加平稳地通过截面，从而减小旋涡的强度以及规模。

由图15可知，在0°风攻角下，增设风嘴后与增设风嘴加水平导流板后的流线图类似。尾迹区周期性的旋涡脱落消失，主梁上表面的旋涡消失，下表面的旋涡也变得稳定，从而抑制了涡振发生。

在主梁两边增设上L型导流板后，由图16可知，在0°风攻角下，来流在上L型导流板处分离，上表面气流在主梁上方形成一对旋涡。下表面气流在上L板下形成一对小涡，气流运动至边主梁时，再次发生分离，在主梁下表面形成多个小涡以及一个大尺寸旋涡，旋涡形状与原始断面类似。气流运动至尾迹区时，由于尾部上L板的存在，改变了尾迹区的流线轨迹，进而使得周期性脱落消失。

5 结 论

（1）小阻尼比与规范规定阻尼比下的涡振试验研究表明：提高阻尼比可以显著降低主梁的竖弯和扭转涡振振幅，从而改善了主梁的涡振性能。

（2）风洞试验以及数值模拟结果表明，Π型主梁断面本身具有气动不稳定性，在没有采取抑振措施的情况下，原始断面容易出现明显的涡激振动现象。

（3）风洞试验结果表明，在采取三种不同气动措施后，除采用上L型导流板断面在+3°风攻角下发生扭转涡振外，其余断面均能使得来流平稳地通过，从而抑制涡振的发生。

（4）通过风洞试验研究与数值模拟分析，同时考虑适用性和经济性，上L型导流板为最优选择。该方案下主梁虽仍会发生涡振，但采用该方案后主梁涡振性能得到显著提升，振幅满足规范要求。

需要说明的是，以上结论为本研究通过缩尺模型风洞试验与数值模拟所得，该结论并不能完全适用于实桥涡振性能的评价，仅可为实桥涡振性能评价提供一定参考。

参考文献：

［1］汪志雄， 张志田， 郄凯，等. Π型开口截面斜拉桥弯扭耦合涡激共振及气动减振措施研究［J］. 振动与冲击， 2021， 40（1）： 52-57.

WANG Zhixiong， ZHANG Zhitian， QIE Kai， et al. Bending-torsion coupled vortex induced resonance of Π-type open section cable stayed and aerodynamic vibration reduction measures［J］. Journal of Vibration and Shock， 2021， 40（1）： 52-57.

［2］张天翼， 孙延国， 李明水，等. 宽幅双箱叠合梁涡振性能及抑振措施试验研究［J］. 中国公路学报， 2019， 32（10）： 107-114.

ZHANG Tianyi，SUN Yanguo，LI Mingshui，et al. Experimental study on vortex-induced vibration performance and aerodynamic countermeasures for a wide-width double-box composite beam［J］. China Journal of Highway and Transport， 2019， 32（10）： 107-114

［3］贺耀北， 周洋， 华旭刚. 双边钢主梁-UHPC组合梁涡振抑制气动措施风洞试验研究［J］. 振动与冲击， 2020， 39（20）： 142-148.

HE Yaobei，ZHOU Yang，HUA Xugang. A wind tunnel test on aerodynamic measures for vortex-induced vibration suppression of a bilateral steel-UHPC composite beam［J］. Journal of Vibration and Shock， 2020， 39（20）： 142-148.

［4］Bai H，Li R，Xu G J，et al. Aerodynamic performance of Π-shaped composite deck cable-stayed bridges including VIV mitigation measures［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2021， 208： 104451.

［5］李永乐， 侯光阳， 向活跃， 等. 大跨度悬索桥钢箱主梁涡振性能优化风洞试验研究［J］. 空气动力学学报， 2011， 29（6）： 702-708.

LI Yongle，HOU Guangyang，XIANG Huoyue，et al. Optimization of the vortex induced vibration for steel box girder of long span suspension bridges by wind tunnel test［J］. Acta Aerodynamica Sinica，2011，29（6）：702-708

［6］段青松， 马存明. 边箱叠合梁涡振性能及抑振措施研究［J］. 桥梁建设， 2017， 47（5）： 30-35.

DUAN Qingsong，MA Cunming. Study of vortex-induced vibration performance and vibration suppression measures for composite girder with edge boxes［J］. Bridge Construction， 2017， 47（5）： 30-35.

［7］董锐， 杨詠昕， 葛耀君. 斜拉桥Π型开口断面主梁气动选型风洞试验［J］. 哈尔滨工业大学学报， 2012， 44（10）： 109-114.

DONG Rui，YANG Yongxin，GE Yaojun. Wind tunnel test for aerodynamic selection of Π shaped deck of cable-stayed bridge［J］. Journal of Harbin Institute of Technology， 2012， 44（10）： 109-114.

［8］钱国伟， 曹丰产， 葛耀君. Π型叠合梁斜拉桥涡振性能及气动控制措施研究［J］. 振动与冲击， 2015， 34（2）： 176-181.

QIAN Guowei，CAO Fengchan，GE Yaojun. Vortex-induced vibration performance of a cable-stayed bridge with Π shaped composite deck and its aerodynamic control measures［J］. Journal of Vibration and Shock， 2015， 34（2）： 176-181.

［9］谭彪， 操金鑫， 檀小辉，等. 间距比对叠合梁双幅桥涡振性能的影响［J］. 同济大学学报（自然科学版）， 2020， 48（9）： 1264-1270.

TAN Biao，CAO Jinxin，TAN Xiaohui，et al. Effect of gap distance ratio on vortex-induced vibration performance for bridge with twin composite girders［J］. Journal of Tongji University （Natural Science）， 2020， 48（9）： 1264-1270.

［10］张志田， 卿前志， 肖玮， 等. 开口截面斜拉桥涡激共振风洞试验及减振措施研究［J］. 湖南大学学报（自然科学版）， 2011， 38（7）： 1-5.

ZHANG Zhitian，QING Qianzhi，XIAO Wei，et al. Vortex-induced vibration and control method for a cable-stayed bridge with open cross section［J］. Journal of Hunan University（Natural Sciences）， 2011， 38（7）： 1-5.

［11］中华人民共和国交通运输部. 公路桥梁抗风设计规范：JTG/T 3360-01—2018［S］. 北京：人民交通出版社， 2019.

Ministry of Transport of the Peoples Republic of China. Wind-resistant design specification for highway bridges： JTG/T 3360-01—2018［S］. Beijing： China Communications Press， 2019.

［12］赵林， 李珂， 王昌将， 等. 大跨桥梁主梁风致稳定性被动气动控制措施综述［J］. 中国公路学报， 2019， 32（10）： 34-48.

ZHAO Lin，LI Ke，WANG Changjiang，et al. Review on passive aerodynamic countermeasures on main girders aiming at wind-induced stabilities of long-span bridges［J］. China Journal of Highway and Transport， 2019， 32（10）： 34-48.

［13］战庆亮， 周志勇， 葛耀君. 开口叠合梁断面气动性能的试验研究［J］. 桥梁建设， 2017， 47（1）： 17-22.

ZHAN Qingliang，ZHOU Zhiyong，GE Yaojun. Experimental study of aerodynamic performance of open cross sections of composite girders［J］. Bridge Construction， 2017， 47（1）： 17-22.

［14］黄林， 董佳慧， 王骑， 等. 矩形钢箱梁铁路斜拉桥涡振性能及气动控制措施研究［J］. 振动与冲击， 2021， 40（6）： 23-32.

HUANG Lin，DONG Jiahui，WANG Qi，et al. Vortex-induced vibration performance of a cable-stayed railway bridge with rectangular steel box girder and its aerodynamic［J］. Journal of Vibration and Shock， 2021， 40（6）： 23-32.

［15］孟晓亮， 郭震山， 丁泉顺， 等. 风嘴角度对封闭和半封闭箱梁涡振及颤振性能的影响［J］. 工程力学， 2011， 28（增刊1）： 184-189.

MENG Xiaoliang，GUO Zhenshan，DING Quanshun，et al. Influence of wind fairing angle on vortex-induced vibrations and flutter performances of closed and semi-closed box decks［J］. Engineering Mechanics， 2011， 28（Sup1）： 184-189.

［16］张建， 郑史雄， 唐煜， 等. 基于节段模型试验的悬索桥涡振性能优化研究［J］. 实验流体力学， 2015， 29（2）： 48-54.

ZHANG Jian，ZHENG Shixiong，TANG Yu，et al. Research on optimizing vortex-induced vibration performance for suspension bridge based on section model test［J］. Journal of Experiments in Fluid Mechanies， 2015， 29（2）： 48-54.

Vortex-induced vibration performance and aerodynamic countermeasures of Π-shaped composite girder of a cable-stayed bridge

Abstract： Π-shaped composite deck is an elastic bluff body， which is susceptible to aerodynamic instability. In the present study， a cable-stayed bridge with a Π-shaped composite deck is taken as the research object， and the vortex-induced vibration （VIV） and the aerodynamic countermeasures are investigated by using the small-scale wind tunnel tests and computational fluid dynamics （CFD） method. The wind speed range of the VIV for the Π-shaped composite deck is determined via the wind tunnel test. After that， several VIV mitigation measures are investigated. The computational fluid dynamics （CFD） method is used to study the mechanism of VIV and vibration suppression by aerodynamic measures. The results indicate that the VIV in the original section is caused by the interaction of the periodic shedding of the vortex in the wake area and the vortex evolution on the upper and lower surfaces of the girder； After adopting three different aerodynamic measures， the flow can pass through the section more smoothly， so as to mitigate the VIV effectively， except for the upper inverted L-shaped guide plate at the wind attack angle of +3°. This study can offer guidance on the wind-resistant design of a cable-stayed bridge with a Π-shaped composite deck.

Key words： vortex-induced vibration （VIV）；vibration-reduction measures；composite girder；wind tunnel test；computational fluid dynamics （CFD）