变截面压电悬臂梁能量采集器在高斯白噪声激励下的稳态统计特性研究
周坤涛 杨涛 葛根 郝淑英 冯晶晶 张琪昌
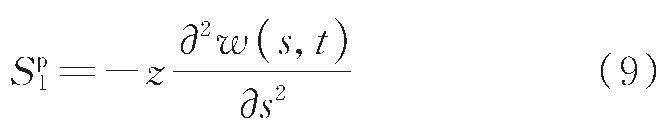
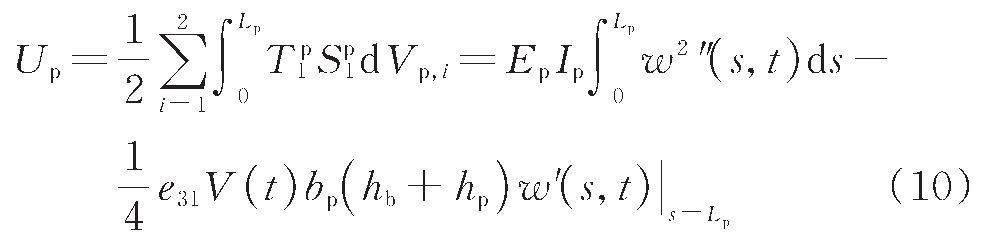
摘要: 环境振动是一种非周期、随机的宽频激励,研究振动能量采集器在环境振动下的能量采集特性具有重要意义。本文采用改进随机平均法,求解了变截面压电梁在高斯白噪声激励下的等效振幅、位移、速度的稳态概率密度函数,位移与速度的联合概率密度函数以及稳态均方输出电压,随后研究了变截面压电梁的能量采集效能。结果表明:负载电阻一定时,截面系数β>0时的变截面压电梁相比β=0时的等截面压电梁有更好的稳态均方输出电压;截面系数β>0时,随着电阻电容乘积的倒数的增加,变截面压电梁的均方电压均呈现逐渐减小的趋势,当电阻电容乘积的倒数值一定时,β值越大,均方电压也越高;随着噪声强度的增加,变截面压电梁的均方电压均呈现逐渐增大的趋势,当噪声强度一定时,β值越大,均方电压也越高。本文研究结果可为变截面压电悬臂梁能量采集系统的设计及应用提供理论依据。
关键词: 能量采集器; 变截面压电悬臂梁; 高斯白噪声激励; 稳态概率密度; 均方电压
中图分类号: O324; TB34; TM91 文献标志码: A 文章编号: 1004-4523(2024)05-0864-11
DOI:10.16385/j.cnki.issn.1004-4523.2024.05.015
引 言
压电振动能量采集器是一种利用压电陶瓷元件的压电效应将采集到的环境中的振动能转换成电能的机电耦合器件。该器件具有能量密度高、结构简单、体积小等优点,被广泛应用于无线传感器、MEMS等微功耗电子产品的供电系统中,成为目前微能源领域的研究热点[1]。
国内外学者对压电能量采集器做了大量的研究,取得了丰硕的成果。Erturk等[2?3]对线性压电悬臂梁能量采集器做了系统的研究,推导了电压及功率的表达式,研究表明,线性能量采集器的工作频带窄、能量转换效率低,不满足微功耗器件的供电要求。为此,学者们提出了双稳态非线性压电振动能量采集器,其主要原理是将线性能量采集器末端引入一对相互排斥的磁铁,通过调节两磁铁的间距从而产生非线性恢复力,使得该系统具有两个势阱,研究发现,双稳态运动大大提高了系统的频率响应范围,提升了能量的采集效率,同时双稳态压电振动能量采集器的输出性能严重依赖外部振动强度[4]。此后学者们进一步提出了具有更浅、更宽势阱的三稳态[5]、四稳态[6]压电振动能量采集器,并深入研究了多稳态能量采集器的输出性能和非线性动力学行为。
除了辅磁力导致的非线性力之外,学者们还通过优化悬臂梁的几何形状来提高能量采集效率。众所周知,等截面形式的压电梁在长度方向上无法使应力分布均匀化,导致其不能最大程度地利用压电材料有效地提升能量采集效率。为提升压电梁应力应变分布的均匀性,学者们开展了很多等截面压电梁结构的优化设计研究,发现变截面梁的应变分布比等截面梁更均匀。Roundy等[7]通过改变悬臂梁结构的几何形状,发现梯形截面提供的能量是矩形截面的两倍(每单位体积PZT)。Baker等[8]对相同体积的矩形和梯形悬臂梁进行了实验研究,结果表明,与同体积矩形悬臂梁相比,梯形压电悬臂梁的输出能量提高了约30%。Zhang等[9]采用理论与实验相结合的方法研究了一阶频率较低、输出电压和功率高于矩形梁的梯形悬臂式压电能量采集器。Kundu等[10]通过改变悬臂式压电振动能量采集器的厚度,实现了沿梁长方向的均匀应力,与等厚度压电能量采集器相比发电功率显著提高。谭杨康等[11]利用数值仿真和试验测试相结合的方法研究了梯形梁俘能器的性能。
上述文献大都研究了压电悬臂梁在确定性的简谐激励下的响应和输出特性,但在大多数情况下,环境振动是一种非周期、随机的宽频激励,因此有必要研究压电能量采集器在随机振动下的能量采集特性。国外学者Daqaq[12]给出了压电振动能量俘获器在高斯白噪声激励下的响应统计数据,研究发现刚度非线性对系统的平均功率具有重要影响。国内学者孙舒等[13]通过数值模拟研究了白噪声激励下双稳态压电发电系统的响应特性,发现噪声强度的增加会减少双稳态系统两个稳定平衡点之间的跳跃时间。Jiang等[14?15]针对高斯白噪声激励下的非线性振动能量采集器提出了一种随机平均方法,利用广义谐波函数发展了随机平均方法。Su等[16]采用随机平均法研究了高斯白噪声激励下单稳态压电能量收集系统,揭示了其物理机理。刘迪等[17]研究了高斯白噪声作用下非对称单稳态能量采集器的概率响应。然而在已有的研究中,关于变截面压电梁在随机激励下的能量采集特性方面的研究鲜有报道。
本文以根部粘贴双晶压电片,基底层线性变宽度的变截面悬臂梁为研究对象,考虑压电材料的线性本构关系以及梁基底层的几何非线性。首先采用拉格朗日法建立变截面压电梁在高斯白噪声激励下的振动方程及压电方程;其次将振动方程中的电压项表示成位移和速度的解耦项,构建振动系统的哈密顿(Hamilton)总能量,将瞬时频率表达式转化成形式更为简洁的平均频率表达式,通过引入坐标变换导出关于瞬时振幅和瞬时相位的一组随机微分方程;最后利用随机平均法将其简化为等效振幅的伊藤(It?)方程,随后基于FPK方程求解稳态响应的概率密度,分别求解变截面压电梁与等截面压电梁的等效振幅、位移、速度的稳态概率密度函数以及压电梁速度和位移的联合概率密度函数。计算了负载电阻一定时,变截面梁与等截面梁的均方电压值;分析了截面系数β>0的变截面压电梁在电阻电容乘积的倒数及噪声强度变化时的稳态均方电压的输出规律,将计算得到的近似解析解与随机龙格?库塔法数值模拟结果进行对比,验证了理论的可靠性。
1 物理建模
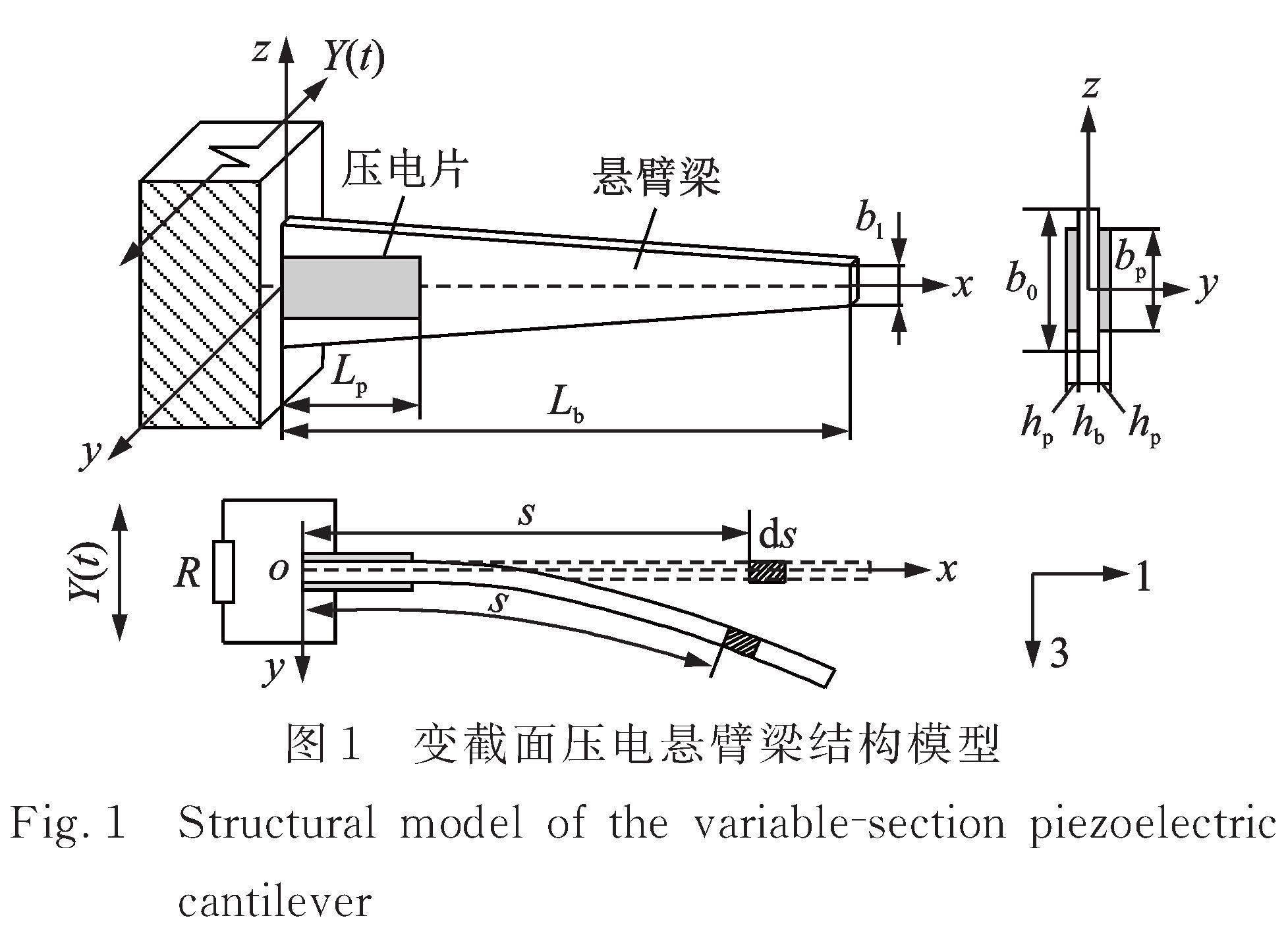
图1所示为双晶Euler?Bernoulli变截面压电悬臂梁能量采集器。极化方向相反的两片压电陶瓷片分别粘结在基底层的上下表面,且串联连接于外部负载电阻R,其中,压电片的长度为Lp,宽度为bp,厚度为hp;基底层为宽度沿水平方向逐渐变窄的变截面悬臂梁,其固定端宽度为b0,自由端宽度为bl,厚度为hb,长度为Lb。建立图1所示直角坐标系,x轴位于梁的中性轴,y轴沿梁厚度方向,z轴沿梁宽度方向,s为沿梁长度方向固定在中性轴上的弧坐标,ds为弧坐标s处的微元段,Y(t)为横向基座的白噪声激励,其中,1方向表示轴向,3方向表示横向。
定义基底层截面系数![]() ,则该压电悬臂梁在坐标
,则该压电悬臂梁在坐标![]() 处的横截面积
处的横截面积![]() 和截面惯性矩
和截面惯性矩![]() 分别表示如下:
分别表示如下:
悬臂梁上的双晶压电片随结构在外激励力作用下做横向弯曲振动,压电层的动应变将通过电极产生交变的输出电压,通过适当整流或滤波即可转换成稳定的整流电压,则压电本构方程可以表示为:
式中![]() 为压电材料在1方向上的应力;
为压电材料在1方向上的应力;![]() 为压电材料在1方向上的应变;
为压电材料在1方向上的应变;![]() 为压电片的弹性模量;
为压电片的弹性模量;![]() 为压电片压电常数;
为压电片压电常数;![]() 为3方向上的电位移;
为3方向上的电位移;![]() 为压电片介电常数;
为压电片介电常数;![]() 为3方向上的电场强度。
为3方向上的电场强度。
假设每片压电陶瓷片在![]() 方向上的电场强度是均匀分布的,则有:
方向上的电场强度是均匀分布的,则有:
![]() (3)
(3)
式中![]() 为采集器输出电压。
为采集器输出电压。
图1中压电梁的物理参数如表1所示。忽略梁的重力效应和转动效应,高斯白噪声激励下理论上梁的每一阶模态都能被激励出来,考虑环境振动为低频振动,悬臂梁一阶弯曲振动模态占主导作用,高阶模态通常影响较小[6],因此本文只考虑梁的一阶模态振动。
在高斯白噪声![]() 激励下,压电梁基底层的动能
激励下,压电梁基底层的动能![]() 可表示为:
可表示为:
压电陶瓷片的动能![]() 可表示为:
可表示为:
式中 上标“![]() ”表示对时间
”表示对时间![]() 求偏导;
求偏导;![]() 和
和![]() 分别为变截面梁和压电片的密度;
分别为变截面梁和压电片的密度;![]() 为横向位移。
为横向位移。
基底较长,悬臂梁的挠度可设为中等挠度,基底层梁振动时的弯矩为:
式中 上标“ ' ”表示对![]() 求偏导;
求偏导;![]() 为变截面梁的弹性模量。
为变截面梁的弹性模量。
基底层梁的弯曲势能![]() 为:
为:
将式(6)代入式(7)中,略去高阶小量,可得:
压电片较短,且位于悬臂梁的根部,变形时非线性不明显,由Euler?Bernoulli梁理论,压电片上任意一点![]() 的轴向应变
的轴向应变![]() 可表示为:
可表示为:
压电片的弹性势能![]() 可表示为:
可表示为:
式中![]() 为第
为第![]() 片压电片的体积。
片压电片的体积。
压电片产生的电势能![]() 可表示为:
可表示为:
式中![]() 为压电片的电容。
为压电片的电容。
距离基座s处的压电悬臂梁横向位移![]() 可表示为:
可表示为:
?![]() (12)
(12)
式中![]() 为振型函数;
为振型函数;![]() 为梁横向振动模态坐标。
为梁横向振动模态坐标。
运用Lagrange方程建立变截面压电悬臂梁能量采集器的运动方程,即
考虑广义耗散力与广义速度的大小成正比,与速度方向成反比,可以得到:
式中![]() 为分布的黏性外阻尼系数。由于压电片串联连接外部电阻
为分布的黏性外阻尼系数。由于压电片串联连接外部电阻![]() ,则有:
,则有:
将式(4)~(5),(8),(10)~(12),(14)~(15)代入式(13),可得双晶压电梁的振动微分方程为:
其中:
其中,变截面梁的振型函数可参考文献[18]的方法进行求解。
2 改进随机平均法
由于外激![]() 是一种特殊的随机过程,无法给出响应的确定性描述,工程中处理这种随机问题时一般将激励的统计特性与响应的统计特性联系起来。本文压电梁基底层变形属于中等变形,建模时考虑了弯曲非线性,因此采用改进随机平均法研究系统在宽带有界噪声激励下的响应[19] 。
是一种特殊的随机过程,无法给出响应的确定性描述,工程中处理这种随机问题时一般将激励的统计特性与响应的统计特性联系起来。本文压电梁基底层变形属于中等变形,建模时考虑了弯曲非线性,因此采用改进随机平均法研究系统在宽带有界噪声激励下的响应[19] 。
为方便起见,下文中无量纲时间![]() 仍写为
仍写为![]() ,假设式(17)的解为:
,假设式(17)的解为:
(18)
式中![]() ,
,![]() ,
,![]() 为随机瞬时等效振幅;
为随机瞬时等效振幅;![]() 为随机角频率;
为随机角频率;![]() 为随机相位。
为随机相位。
对式(18)求时间的导数,可得:
将式(18)和(19)代入式(17)中的第二式,可得:
则电压u可表示为:
将式(21)代入式(17)中的第一式,可得:
式(22)的动能为:
式(22)保守力的势能为:
则哈密顿函数为:
将式(18)中![]() 和式(19)中
和式(19)中![]() 的表达式代入式(25)中,当
的表达式代入式(25)中,当![]() 时,哈密顿函数为:
时,哈密顿函数为:
当![]() 时,哈密顿函数为:
时,哈密顿函数为:
显然处于稳态时,![]() 恒成立,可以解得:
恒成立,可以解得:
通常情况下,比较系数![]() 和
和![]() 可以发现,
可以发现,![]() ,则式(29)可以简化为:
,则式(29)可以简化为:
将式(30)代入式(20),通过泰勒展开,忽略高次项,可得电压的振幅B为:
通过坐标变换,式(22)可变为:
其中:
式(32)中,振幅![]() 在半无限时间区间上弱收敛于一个马尔可夫扩散过程。该扩散过程受下列伊藤微分方程支配:
在半无限时间区间上弱收敛于一个马尔可夫扩散过程。该扩散过程受下列伊藤微分方程支配:
![]() (33)
(33)
式中![]() 为漂移系数;
为漂移系数;![]() 为扩散项;
为扩散项;![]() 为标准单元布朗运动,其中:
为标准单元布朗运动,其中:
对于高斯白噪声,其强度为![]() ,均值为0,互相关函数
,均值为0,互相关函数![]() 可表示为:
可表示为:
式中![]() 表示期望,
表示期望,![]() 表示狄拉克函数。
表示狄拉克函数。
通过改进随机平均法计算后,振幅过程![]() 满足独立的伊藤微分方程表达式(33),其中漂移系数
满足独立的伊藤微分方程表达式(33),其中漂移系数![]() 和扩散系数
和扩散系数![]() 分别表示为:
分别表示为:
其中,各系数分别为:
3 稳态概率密度函数
关于伊藤方程式(33),其平均后的FPK方程可以表示为:
式中 常数![]() 为归一化系数。
为归一化系数。
将![]() 和
和![]() 的表达式代入式(39),可得等效振幅的稳态概率密度函数
的表达式代入式(39),可得等效振幅的稳态概率密度函数![]() 为:
为:
考虑式(31),可得电压振幅的稳态概率密度函数![]() 为:
为:
哈密顿能量包线概率密度可表示为:
位移![]() 和速度
和速度![]() 的联合稳态概率密度可由哈密顿函数的稳态概率
的联合稳态概率密度可由哈密顿函数的稳态概率![]() 得:
得:
由式(21)和(43),可得到稳态均方电压为:
4 变截面压电梁能量采集随机响应分析
4.1 高斯白噪声信号模拟
理想的白噪声具有无限带宽,现实中通常将有限带宽的平整信号视为白噪声,因此数字模拟的白噪声信号一般是具有一定截止频率的限带白噪声。本文采用独立的单位正态随机序列![]() 模拟高斯白噪声[15]:
模拟高斯白噪声[15]:
式中 D为噪声强度;![]() 为时间间隔;
为时间间隔;![]() 为n个符合正态分布的随机数。图2为模拟的高斯白噪声信号。
为n个符合正态分布的随机数。图2为模拟的高斯白噪声信号。
4.2 随机响应分析
采用Euler差分法对式(17)进行求解,噪声强度D为0.002,时间步长Δt为0.01,阻尼比ζ为0.025,外接电阻为1 MΩ,初始位移、速度、电压均为零,具体参数如表2所示。通过计算得到高斯白噪声激励下变截面压电能量采集器的相图和瞬时功率P的时间历程图,如图3所示。
从图3(a),(c),(e)所示的相图中可以看出,相同噪声强度激励下,β=0.5时的压电梁振动位移和速度最小,β=0时的压电梁次之,β=-0.5时的压电梁最大;从图3(b),(d),(f)所示的瞬时功率图中可以看出,β=0.5时的压电梁瞬时功率最大,β=0时的压电梁次之,β=-0.5时的压电梁最小。
5 变截面压电梁能量采集稳态统计特性分析
5.1 变截面与等截面压电梁振动特性与电输出特性分析
采用随机龙格?库塔法进行数值模拟,选取与上文相同的参数,分析基底层梁截面系数β分别为0.5,0,-0.5时压电梁的稳态概率密度及均方电压值。数值模拟时,随机选取1500组白噪声信号,其中每组信号含有20000个点,模拟时间步长Δt为0.01,对式(17)进行激励,选取每组噪声激励后的10000个点作为稳态响应,最后对这1500×10000个点进行振幅A、位移x、速度y的稳态概率密度统计,结果如图4所示。
由图4(a)可知,压电梁截面系数β从0.5到-0.5的变化过程中,振幅的稳态概率密度图缓慢向右偏移,均值逐渐增大,其方差也逐渐增大。从而推断出:变截面压电梁自由端从窄变宽的过程中振幅越来越大。从图4(b),(c)中可以看出,位移和速度的稳态概率密度图的均值不变,方差越来越大,可以推断出位移和速度的振动范围越来越宽。本文解析法和随机龙格?库塔法分析的变截面压电梁在相同噪声激励下的振动规律与上文中Euler法数值模拟的相图结果相符。
通过式(43)与随机龙格?库塔法,本文进一步对β分别为0.5,0,-0.5时压电梁的位移和速度的联合概率密度进行了分析,结果如图5所示。
由图5可知,在β从0.5到-0.5的变化过程中,联合概率密度函数的图像逐渐变得“矮胖”,表明系统的振幅逐渐增大,而且振动范围也越来越大,所得的结论与振幅、位移及速度的稳态概率密度相符。
当电阻一定时,稳态输出功率与稳态均方电压成比例,因此通过分析均方电压的输出特性可以有效地预测输出功率。本文采用理论与数值的方法计算了截面系数β分别为0.5,0,-0.5时压电梁的稳态均方电压值,其理论解可由式(44)求得,数值解可由龙格?库塔法求得,结果如表3所示。
从表3中可以看出,当负载电阻为1 MΩ,噪声强度为0.002时,基底层截面系数β=0.5时的压电梁与β=0时的压电梁相比,其稳态均方电压理论值提高了133%;基底层截面系数β=-0.5时的压电梁与β=0时的压电梁相比,其稳态均方电压理论值降低了43%。产生这一现象的原因是等截面压电梁振动时弯曲应力主要集中在梁的根部,而变截面压电梁特别是截面系数β>0的梁弯曲时各截面的最大正应力越来越接近。稳态均方电压越高,压电能量采集器的电输出特性越好。通过上述比较发现:基底层截面系数β>0时变截面压电梁有较好的稳态输出功率,该预测结果与Euler法数值模拟的瞬时功率相符,后文将选取β>0时的压电梁进行深入研究。
5.2 电阻电容乘积的倒数对稳态输出功率的影响
为研究电阻电容乘积的倒数对变截面压电梁稳态输出功率的影响,本文按照稳态输出功率与稳态均方电压成比例的特性,探讨了不同截面系数压电梁的稳态均方电压随电阻电容乘积的倒数的变化规律,结果如图6所示。
从图6中可以看出,随着电阻电容乘积的倒数λ的增大,截面系数β≥0时的压电梁均方电压值均呈现逐渐减小的趋势,其中截面系数β=0,0.5,0.7时的压电梁会随着电阻电容乘积的倒数的增大而缓慢下降,而截面系数β=0.9时的压电梁则随着电阻电容乘积的倒数的增大而快速下降。
为研究不同截面系数压电梁在同一λ值时的均方电压输出特性,本文分析了β>0时的压电梁均方电压的理论值较β=0时的变化率,结果如表4所示。
从表4中可以看出,λ=0.2时,与β=0时的压电梁相比,β=0.5时的压电梁理论均方电压值增加了89%,β=0.7时的压电梁增加了186%,而β=0.9时的压电梁则增加了475%。等截面压电梁振动时弯曲应力主要集中在梁的根部,而随着截面系数β的增大,变截面压电梁的弯曲应力会越来越均匀,因此梁截面系数β增大时,均方输出电压也逐渐增大。
5.3 噪声强度对稳态输出功率的影响
为了讨论噪声强度对稳态输出功率的影响,本文探讨了不同截面系数压电梁均方电压随噪声强度的变化规律,结果如图7所示。其中,实线为解析解,由式(44)求得,虚线为数值解。
从图7中可以看出,随着噪声强度D的增大,均方电压均线性增大,且β>0时的压电梁均方电压明显高于β=0时的压电梁。
为研究不同截面系数压电梁在同一D值时的均方电压输出特性,本文分析了β>0时的压电梁均方电压的理论值较β=0时的变化率,结果如表5所示。
从表5中可以看出,D=0.005时,与β=0时的压电梁相比,β=0.5时的压电梁理论均方电压值增加了71.9%,β=0.7时的压电梁增加了145.5%,而β=0.9时的压电梁则增加了369%。
6 试验研究
图8为变截面压电能量采集器试验装置。变截面压电悬臂梁一端紧固在L形夹具上,其基底层(200 mm×20 mm×0.7 mm)采用6061铝合金制作,在基底层根部上下表面粘结大小相同、极化相反的压电陶瓷片(材料为PZT?5,尺寸为38 mm×10 mm×0.2 mm)。在压电梁的末端距离基底层80 mm处安装红外位移传感器(IL?065),整个试验装置通过亚克力板固定在激振器(APS113)上。
图9为搭建的变截面压电梁振动能量采集器测试系统。实验前,利用式(45)将噪声强度D设定为0.004,时间间隔Δt设定为0.01,n设定为1000,采用MATLAB软件,随机生成一组白噪声信号输入到信号发生器(Tectronix AFG3102C)中,该信号经功率放大器(APS 125)放大后输入到激振器中,模拟随机振动;压电能量采集器末端的位移信号经红外传感器测量后输入到示波器(Tectronix DPO2012B)1通道中显示;能量采集器的输出电压输入到示波器2通道中显示;加速度传感器安装在激振器末端的支座上,用以检测激振器的输出信号,通过信号采集器(DH5927N)采集并显示。
为比较等截面压电梁和变截面压电梁在噪声激励下的振动特性与电输出特性,分别选取截面系数β为0和0.5的压电梁进行随机激励实验,将信号发生器的频率设定为3 Hz,通过调节功率放大器的电流和电压旋钮控制激振器的振动幅度,每组实验通过观察加速度信号的标准差以确保激振器振动的幅度相同。通过实验得到位移和输出电压的时间历程图,如图10和11所示。
从图10中可以看出,在同一噪声强度激励下,β=0时的压电梁振动位移明显高于β=0.5时的压电梁。从图11中可以看出,β=0时的压电梁输出电压低于β=0.5时的压电梁,实验结果与本文理论统计预测结果相符。
7 结 论
本文利用改进随机平均法分析了噪声激励下变截面压电梁的稳态响应特性,通过理论计算和数值模拟得到了如下结论:
(1)改进后的随机平均法适用于噪声激励下变截面压电悬臂梁能量采集器的稳态响应分析。
(2)负载电阻R为1 MΩ时,均方电压值的大小依次为β=0.5,β=0,β=-0.5,结果表明,截面系数β>0时的变截面压电梁有较好的稳态均方输出电压,相对于等截面梁可显著提升能量采集效能;β<0时的采集效能弱于等截面梁。
(3)截面系数β>0时,随着电阻电容乘积的倒数的增大,变截面压电梁的均方电压均呈现逐渐减小的趋势,且β越大,均方电压下降得越快。当λ的值一定时,随着β的增大,变截面压电梁的均方电压也增大,且均高于等截面压电梁的均方电压。
(4)截面系数β>0时,随着噪声强度的增大,均方电压线性增大,且变截面压电梁的均方电压均高于等截面压电梁的均方电压。
参考文献:
[1]杨涛, 周生喜, 曹庆杰, 等. 非线性振动能量俘获技术的若干进展[J]. 力学学报, 2021, 53(11): 2894-2909.
Yang Tao, Zhou Shengxi, Cao Qingjie, et al. Some advances in nonlinear vibration energy harvesting technology[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(11): 2894-2909.
[2]Erturk A, Inman D J. On mechanical modeling of cantilevered piezoelectric vibration energy harvesters[J]. Journal of Intelligent Material Systems and Structures, 2008,19(11): 1311-1325.
[3]Erturk A, Inman D J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters[J]. Journal of Vibration and Acoustics, 2008, 130(4): 041002.
[4]唐炜, 王小璞, 曹景军. 非线性磁式压电振动能量采集系统建模与分析[J]. 物理学报, 2014, 63(24): 76-89.
Tang Wei, Wang Xiaopu, Cao Jingjun. Modeling and analysis of piezoelectric vibration energy harvesting system using permanent magnetics[J]. Acta Physica Sinica, 2014, 63(24): 76-89.
[5]Wang G Q, Liao W H, Zhao Z X, et al. Nonlinear magnetic force and dynamic characteristics of a tri-stable piezoelectric vibration energy harvester[J]. Nonlinear Dynamics, 2019, 97: 2371-2397.
[6]谭江平, 王光庆, 鞠洋, 等. 多稳态压电振动能量采集器的非线性动力学特性及其实验研究[J]. 振动工程学报, 2021, 34(4): 765-774.
Tan Jiangping, Wang Guangqing, Ju Yang, et al. Nonlinear dynamic characteristics and experimental validation of a multi-stable piezoelectric vibration energy harvester[J]. Journal of Vibration Engineering, 2021, 34(4): 765-774.
[7]Roundy S, Leland E S, Baker J, et al. Improving power output for vibration-based energy scavengers[J]. IEEE Pervasive Computing, 2005, 4(1): 28-36.
[8]Baker J, Roundy S, Wright P. Alternative geometries for increasing power density in vibration energy scavenging for wireless sensor networks[C]//3rd International Energy Conversion Engineering Conference. San Francisco, California, 2005: 959-970.
[9]Zhang G Y, Gao S Q, Liu H P, et al. A low frequency piezoelectric energy harvester with trapezoidal cantilever beam: theory and experiment[J]. Microsystem Technologies, 2017, 23: 3457-3466.
[10]Kundu S, Nemade H B. Piezoelectric vibration energy harvester with tapered substrate thickness for uniform stress[J]. Microsystem Technologies, 2021, 27(1): 105-113.
[11]谭杨康, 高世桥, 张广义. 梯形梁压电俘能器的特性研究[J]. 压电与声光, 2016, 28(4): 579-583.
Tan Yangkang, Gao Shiqiao, Zhang Guangyi. Study on the characteristics of trapezoidal cantilever piezoelectric energy harvester[J]. Piezoelectrics & Acoustooptics, 2016, 28(4): 579-583.
[12]Daqaq M F. On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations[J]. Nonlinear Dynamics, 2012, 69(3): 1063-1079.
[13]孙舒, 曹树谦. 白噪声激励下双稳态压电发电系统的响应分析[J]. 压电与声光, 2015, 37(6): 969-972.
Sun Shu, Cao Shuqian. The response analysis of bistable piezoelectric power generation system under white noise excitation[J]. Piezoelectrics & Acoustooptics, 2015, 37(6): 969-972.
[14]Jiang W A, Chen L Q. Stochastic averaging based on generalized harmonic functions for energy harvesting systems[J]. Journal of Sound and Vibration, 2016, 377: 264-283.
[15]Jiang W A, Chen L Q. An equivalent linearization technique for nonlinear piezoelectric energy harvesters under Gaussian white noise[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(8): 2897-2904.
[16]Su M, Xu W, Zhang Y. Theoretical analysis of piezoelectric energy harvesting system with impact under random excitation[J]. International Journal of Non-linear Mechanics, 2020, 119: 103322.
[17]刘迪, 胡美. 高斯白噪声下非对称单稳态能量采集系统的随机响应分析[J]. 山西大学学报(自然科学版), 2022, 45(4): 947-953.
Liu Di, Hu Mei. Stochastic response analysis of asymmetric monostable energy harvesting system driven by Gaussian white noise[J]. Journal of Shanxi University(Natural Science Edition), 2022, 45(4): 947-953.
[18]周坤涛, 杨涛, 葛根. 基于新型振型函数的渐细变截面悬臂梁的自由振动理论与实验研究[J]. 工程力学, 2020, 37(3): 28-35.
Zhou Kuntao, Yang Tao, Ge Gen. Theoretical and experimental study on free vibration of cantilever tapered beam base on new modal function[J]. Engineering Mechanics, 2020, 37(3): 28-35.
[19]Ge G, Li Z P. A modified stochastic averaging method on single-degree-of-freedom strongly nonlinear stochastic vibrations[J]. Chaos, Solitons & Fractals, 2016, 91: 469-477.
[20]He J H. Preliminary report on the energy balance for nonlinear oscillations[J]. Mechanics Research Communications, 2002, 29: 107-111.
[21]Zhu W Q. Recent developments and applications of the stochastic averaging method in random vibration[J]. Applied Mechanics Reviews, 1996, 49(10): 72-80.
[22]Huang Z L, Zhu W Q. Stochastic averaging of quasi-integrable Hamiltonian systems under combined harmonic and white noise excitations[J]. International Journal of Non-linear Mechanics, 2004, 39(9): 1421-1434.
Study on the steady state statistical characteristics of variable-section piezoelectric cantilever energy harvester under Gaussian white noise excitation
Abstract: Environmental vibration is one of the non-periodic and random broadband excitations. It is of great significance to study the characteristics of vibration energy harvesters under environmental vibrations. In this paper, the modified stochastic averaging method is used to solve the following parameters of piezoelectric beam with a variable cross-section: steady-state probability density function of equivalent amplitude, displacement and velocity, joint probability density function of displacement, and velocity and steady-state mean square output voltage. Then the study investigates the energy acquisition efficiency of a piezoelectric beam with a variable cross-section under Gaussian white noise excitation. The results show that when the load resistance reaches a certain value, the variable section piezoelectric beam with a section coefficient β>0 can produce better steady-state mean square output voltage than the constant section piezoelectric beam with β=0; when the section coefficient β>0, with the increase of the reciprocal of the product of resistance and capacitance, the mean square voltage of the variable-section piezoelectric beam shows a gradually decreasing trend. The trend shows the following rules: when the reciprocal value of the resistance and capacitance reaches a certain value, the larger the β value is, the higher the mean square voltage will become; with the increase of the noise intensity, the mean square voltage of the variable-section piezoelectric beams shows a trend of increasing gradually; when the noise intensity reaches a certain value, the larger the β value is, the higher the mean square voltage will become. The research results in this paper can provide a theoretical basis for the design and application of the variable-section piezoelectric cantilever energy harvesting system.
Key words: energy harvester;variable-section piezoelectric cantilever;Gaussian white noise excitation;steady-state probability density;mean square voltage

