黏弹性地基上双模量梁受迫振动的时域微分求积法求解

黄春林 彭建设

收稿日期：2023-01-19

基金项目：四川省自然科学基金（2022NSFSC1968）

作者简介：黄春林（1996—），男，硕士，从事计算固体力学研究.Email： huangchunlin2023@163.com

摘要：以欧拉—伯努利梁模型和黏弹性地基模型为基础，说明了黏弹性地基上双模量梁在振动过程中有效抗弯刚度不变，推导出中性层在梁内部时，双模量梁在地基上的受迫振动控制方程.利用其中性层跳变时位移和速度没有突变，用时域微分求积法求解了控制方程，并分别探讨了地基的线性刚度和剪切参数，以及双模量特性对简支双模量梁受迫振动的影响.结果表明，地基的2个参数越大，受迫振动到达稳定的时间越短；双模量比值越大，受迫振动幅值越小.

关键词：双模量梁；地基梁；受迫振动；微分求积法

中图分类号：O302;O321

文献标志码：A

0引言

一些多晶石墨、高聚合物和复合材料具有拉压弹性模量不同的特性，但是在工程应用中一般不考虑材料的双模量特性，这可能导致某些结构设计存在安全隐患［1］.这类双模量力学问题的求解依赖于中性层位置.基于Ambartsumyan的双线性本构模型，在梁振动问题方面已有相关研究.Lucchesi等［1］证明了除无张力材料外，双模量杆的纵向振动存在唯一解.Yang等［2］用光滑函数法避免本构关系不连续，研究了双模量杆的纵向振动.刘相斌等［3］和王铭慧等［4］用不同方法研究了双模量梁的自由振动.吴晓等［5］在文献［3］的基础上考虑剪切效应研究了双模量梁的自由振动.杨洋等［6］推导出了铁木辛科梁模型下的双模量梁，求解并模拟了双模量梁的前几阶固有频率.文献［7］用微分求积法（DQ法）研究了双参数地基上的双模量梁的频率响应.文献［8］基于双模量梁向上弯曲和向下弯曲时弯矩表达式不变，简单求解了双模量梁的受迫振动.本研究考虑材料的双模量特性，从应变能角度说明矩形等截面的双模量梁在受迫振动过程中有效抗弯刚度不变.基于此，本研究推导了双参数地基上双模量梁的受迫振动控制方程，用时域DQ法求解，并讨论了双参数地基的参数和双模量特性对受迫振动的影响.

1黏弹性地基上双模量梁的控制方程

1.1几何方程

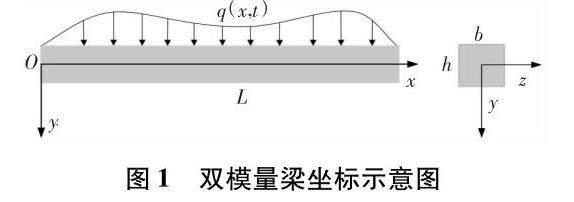
双模量梁长L，横截面宽b，高h（见图1），其材料的拉伸弹性模量和压缩弹性模量分别记为Et和Ec.定义梁几何中面位移为（u0，w0）时，则截面上任意一点的位移可表示为（u，w），小变形时，几何关系为，

u，w=u0－ydwdx，w0（1）

式中，y为横截面上轴向纤维的纵坐标.

那么静态小变形时，应变可表示为，

ε=dudx=ε0－yd2wdx2（2）

式中，ε0=du0dx，为几何中面的应变.需注意双模量梁的中性层不在几何中面.

由弹性力学可知，在图1坐标系下，向下弯曲时，梁的近似曲率为－1ρ0=d2wdx2（ρ0为梁弯曲变形后几何中面的曲率半径）.设中性层到几何中面距离为y0，则由式（2）可得向下弯曲时修正的应变表达式为，

ε=ε0+yρ0=y+y0ρ0（3）

同理，当梁向上弯曲时，近似曲率为1ρ0=d2wdx2，此时向上弯曲时修正的应变表达式为，

ε=ε0－yρ0=y0－yρ0（4）

式（3）和式（4）分别对应图1坐标系下双模量梁向下弯曲和向上弯曲时的应变表达式.其中，式（3）满足当y=-y0时，应变为0；式（4）满足当y=y0时，应变为0.但是中性层的位置y0未知，需要确定.

1.2本构方程

根据文献［2］的广义胡克定律.由式（3）和式（4）结合压缩弹性模量和拉伸弹性模量分别满足下列应力应变关系：

横截面受压缩区域为，

σc=Ecε（5）

横截面受拉伸区域为，

σt=Etε（6）

式中，σt和σc分别为受拉和受压区域的正应力.

1.3地基上双模量梁的应变能

静态小变形时，横截面上的轴力为零，即，

∫AtσtdAt+∫AcσcdAc=0（7）

式中，At和Ac分别表示横截面上的受拉和受压区域的面积.

将式（3）、式（5）和（6）代入式（7），或将式（4）、式（5）和式（6）代入式（7），均可得中性层到几何中面的距离为，

y0=h2Ec－EtEc+Et（8）

由上述确定中性层位置的过程可知，双模量梁向上弯曲和向下弯曲时，几何中面到中性层的距离不变.考虑通常材料的压缩弹性模量大于拉伸弹性模量，此时，梁横截面的应力分布及中性层位置如图2所示.

同理，静态弯曲时横截面上的弯矩可表示为，

∫AtσtydAt+∫AcσcydAc=M（9）

将式（3）、式（5）与式（6）代入式（9），或将式（4）、式（5）和式（6）代入式（9）可得相同的弯矩表达式为，

M = D*d2wdx2 = b24

h + y0 h-2y0 2Ec  + h-y0 h + 2y0 2Et d2wdx2（10）

当y0=0，E=Et=Ec时，上式弯矩表达式可退化为经典欧拉梁的弯矩表达式.由上述确定弯矩的过程可知，双模量梁在振动过程中，随着弯曲方向的变化，中性层位置会跳变［3］，但是弯矩的表达式不变.

因为轴力为0且双模量梁的弯矩可以用1个公式描述，所以振动过程中梁的形变势能可表示为，

Ub=12∫LM2wx2dx=12∫LD*2wx22dx（11）

式（11）经一阶变分处理后得到的常系数，即为梁的有效抗弯刚度.因为弯矩表达式在振动过程中不变，所以有效抗弯刚度D*也不变.由此简化控制方程的推导和求解过程.

1.4受迫振动控制方程

黏弹性地基对双模量梁的反力为，

P=－k1w+k22wx2－cwt（12）

式中，P为地基反力，k1为地基线性刚度系数，k2为地基土剪切系数，c为黏性系数.那么，地基的形变势能为，

Us=12∫Lk1w2+k2wx2+cwtwdx（13）

均布外加载荷q的外力势能为，

Uq=∫Lqwdx（14）

双模量梁的动能为，

K=ρbh∫Lwt2dx（15）

式中，ρ为材料密度.基于哈密顿原理，考虑模量粱的动能、势能和外力做功满足以下关系：

δ∫t0∫LK－Ub+Us－Uqdxdt=0（16）

将式（11）、式（13）、式（14）和式（15）代入式（16）即可推导出双模量梁在黏弹性地基上的横向受迫振动控制方程为，

D*4wx4+k1w－k22wx2+cwt+m2wt2=q（17）

式中，D*是双模量梁的有效抗弯刚度，x是梁沿轴向的自变量，t是时间，w是梁的振动小挠度，m=ρbh是梁单位长度的质量，k1为地基线性刚度，k2为地基剪切参数，c为黏性系数，q为均布动载荷.

式（17）与黏弹性地基上的单模量梁控制方程的主要区别在于有效抗弯刚度不同，当y0=0，E=Et=Ec时，该控制方程可退化为经典地基梁模型.

值得注意的是，由于双模量梁在振动过程中，中性层位置会随着弯曲方向的变化而跳变［3］，所以本模型选择在几何中面建立x坐标轴来避免描述动态位移时挠度函数不连续.从欧拉梁模型来看，小变形受迫振动时只关注中性层的动挠度，而横截面上任一点的动挠度看作与中性层的动挠度相等，因此，选择在双模量梁的几何中面建立x轴来描述动挠度是可行的；从地基上双模量梁的中性层跳变瞬间来看，梁的位移和速度都是连续的，没有突变.综上所述，本研究的黏弹性地基上的双模量梁模型在经典弹性地基梁的基础上，修正了有效抗弯刚度，通过求解控制方程可以近似地求解其受迫振动.

2时域DQ法求解

令ζ=x/L，Γ=t/T，对式（17）无量纲化得：

D4wζ4+k1w－G2wζ2+H1wΓ+H22wΓ2=q（18）

式中，D=D*L4，G=k2L2，H1=cT，H2=mT2.

取未变形时黏弹性地基梁的轴线为ζ空间域，在空间域取Nζ个节点，在Γ时间域取NΓ个节点，则全域有Nζ×NΓ个节点.根据DQ法基本原理，用各节点的加权和表示，可得到全域的DQ线性方程为，

D∑Nζk=1C4ikwk，j+k1wi，j－G∑Nζk=1C2ikwk，j+H1∑NΓl=1C1jlwi，l+H2∑NΓl=1C2jlwi，l=qi，k（19）

式中，i=1，2，···，Nζ;j=1，2，···，NΓ.式中简写的动挠度和动载荷具体形式为α，β=（ζα，Γβ）（=w，q）.由式（19）可得，在全域内有Nζ×NΓ个线性方程组，将式（19）改写为成矩阵形式：

C=F（20）

式中，C是Nζ×NΓ行，列的权系数矩阵；是待定动挠度组成的Nζ×NΓ行的列阵；F是Nζ×NΓ行的广义载荷列阵.以简支边界条件为例，利用黏弹性地基梁在任意时间节点Γj（j=1，2，···，NΓ）都有的4个边界条件和2个初始条件.可将简支梁的边界条件表示为，

ζ=0∶w=0，2wζ2=0（21）

ζ=1∶w=0，2wζ2=0（22）

用DQ法离散为，

w0，Γj=0，∑Nζk=1C21k·wζk，Γj=0w1，Γj=0，∑Nζk=1C2Nζk·wζk，Γj=0 （23）

式中，j=1，2，...，NΓ.

将初始条件设为，

Γ=0∶w=w0，wΓ=v0（24）

用DQ法离散为，

wζi ，0 = w0 ζi ∑Nζ k = 1C（1）1k·wζi ，Γ k  = v0 ζi （25）

式中，i=1，2，…，Nζ.

由式（23）和式（25）得到的4NΓ个边界条件和2Nζ个初始条件，分别取代式（19）中i=1，2，Nζ－1，Nζ表示的线性方程，j=1，2表示的线性方程，得到可解线性方程组，进而得到式（20）的系数矩阵C，从而在全域内求解出挠度列阵，得到已知节点在每个时间节点的函数值.至此，ζ域内所有节点的时程响应已得到.可通过对已得到的ζ域节点在任意时间节点的位移，对时间求一阶偏导，可分别得到Γ域内各节点对应时刻的速度作为下一时间段的初始条件，即可求得下一个时间段的动挠度.

3数值结果与分析

为验证算法和编程，首先将控制方程退化为经典的单模量地基梁情况.以文献［9］的例1为例：两端简支梁，长50 cm，横截面宽1 cm，高2 cm，弹性模量E=1.5×107 N/cm2，质量密度ρ=0.008 kg/cm3，线性刚度k1=3.5×103 N/cm2，剪切参数k2=5.92×104 N，初速度和初位移均为0，在该地基梁上作用以均布载荷q=10sin（500t） N/cm，求该地基梁中点处的位移响应.

验证结果如图3所示，在该梁的1个振动周期0.016 s内该算例的时域DQ法数值解和Galerkin法求得的近似解对比，结果吻合良好.其中，时域DQ法的空间域节点13个，时间域节点21个.

现考虑黏弹性地基上的双模量梁问题：一两端简支的双模量梁，长50 cm，宽1 cm，高2 cm，其拉伸弹性模量Et=2.55×106 N/cm2，压缩弹性模量Ec=5.7×106 N/cm2，质量密度ρ=0.01 kg/cm3，黏性系数c=1.732 5 N·s·cm-2.

算例1上述简支双模量梁位于一黏弹性地基上，在简支梁上作用q=10sin（500t） N/cm均布交变载荷，初始位移和初始速度均为0.地基的剪切参数k2=0，分别求出线性刚度k1为1×103、2×103和4×103 N/cm2时，该梁x=25 cm处的动挠度.

算例2上述简支双模量梁位于一黏弹性地基上，在简支梁上作用q=10sin（500t） N/cm均布交变载荷，初始位移和初始速度均为0.地基的线性刚度k1=1×103 N/cm2，分别求出剪切参数k2为0、6×104和6×105 N时，该梁x=25 cm处的动挠度.

算例3地基的参数同算例1，当上述简支双模量梁位于该地基上时，在简支梁上作用q=1 N/cm的均布突加载荷，求出该梁x=25 cm处的动挠度.

算例4当上述简支双模量梁位于黏弹性地基上，梁上作用q=1 N/cm的均布突加载荷，地基的线性刚度k1=1×103 N/cm2，分别求出剪切参数k2为0、5×104和1×105 N时，该梁x=25 cm处的动挠度.

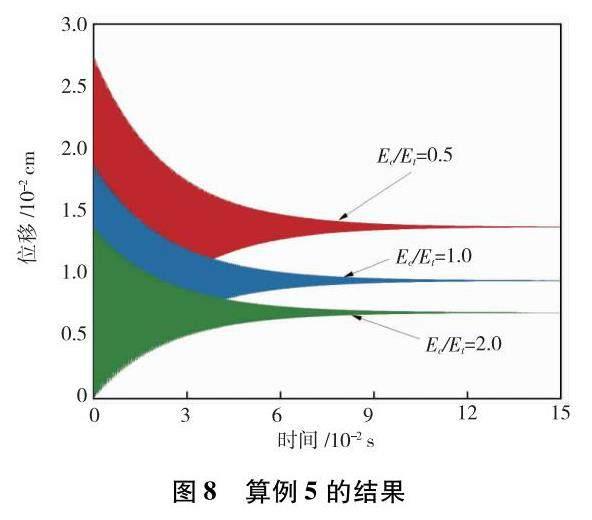
算例5为探讨双模量特性对黏弹性地基梁的影响，简支梁的几何参数、密度与黏性系数同上，地基的线性刚度k1=3×103 N/cm2，剪切系数k2=5×104 N，突加载荷q=1 N.材料的拉伸弹性模量Et=2.55×106 N/cm2，试探讨压缩弹性模量与拉伸弹性模量的比值r=0.5、1和2时该梁的受迫振动.

算例1～算例4均按空间域节点13个，时间域节点51个，求解0.1 s内的振动情况.算例结果分别如图4～图7所示.

将图4和图5对比分析可知，黏弹性地基上简支双模量梁在均布的交变载荷作用下，线性刚度k1对受迫振动的影响强于剪切参数k2；但是线性刚度或剪切参数越大，梁中点处的受迫振动到达稳定的时间越短，且到达稳定时的振动幅值越大.其中，剪切参数按数量级增大才会产生明显的影响.而通过图6和图7对比分析，也验证了地基线性刚度对受迫振动的影响更明显.原因是弹性地基增加了双模量梁的有效刚度，导致系统的频率增大，从而导致振动响应周期减小.

由图8可知，当简支双模量梁在相同突加的均布载荷作用下，地基参数一定时，随着压缩弹性模量Ec与拉伸弹性模量Et的比值增大，振动幅值减小，

且到达稳态的时间缩短.其中Ec∶Et=1时，即为经典单模量时地基梁的受迫振动.该现象是材料的压拉弹性模量比值r越大，双模量梁的有效抗弯刚度越大所导致.

4结论

本研究推导了黏弹性地基上的简支双模量梁的受迫振动控制方程，并基于其中性层跳变时有效抗弯刚度不变，位移和速度无突变的实际现象，用时域DQ法近似求解，并讨论了地基参数和梁材料的压缩与拉伸弹性模量比值对黏弹性地基梁受迫振动的影响，得到以下结论：

1）黏弹性地基的线性刚度对双模量梁受迫振动的影响强于剪切参数，线性刚度的影响起主要作用；而且地基参数越大，双模量梁的刚度就越大，最终使振动到达稳态的时间越短.

2）黏弹性地基上的简支双模量梁受到突加载荷后，其受迫振动的幅值随着双模量的比值增大而减小.出现这种现象的原因是材料的双模量比值越大，梁的有效抗弯刚度越大，从而导致振幅越小.

参考文献：

［1］Lucchesi M，Pagni A.Longitudinal oscillations of bimodular rods［J］.Int J Struct Stab Dy，2005，5（1）：37-54.

［2］Yang H，Wang B.An analysis of longitudinal vibration of bimodular rod via smoothing function approach［J］.J Sound Vib，2008，317（3/5）：419-431.

［3］刘相斌，宋宏伟.不同模量弯曲梁的自由振动［J］.大连民族大学学报，2007，9（5）：104-107.

［4］王铭慧，赵永刚，王康建，等.拉压弹性模量不等材料简支梁的线性振动问题［J］.甘肃科学学报，2014，26（5）：10-13.

［5］吴晓，黄志刚，杨立军.考虑剪切效应时双模量梁的自由振动［J］.振动与冲击，2015，34（24）：160-163.

［6］杨洋，姚文娟.不同模量铁木辛柯梁的自由振动特性分析［J］.上海大学学报（自然科学版），2019，25（6）：978-989.

［7］黄春林，彭建设.双参数弹性地基上双模量梁的频率响应分析［J］.成都大学学报（自然科学版），2020，39（2）：204-208.

［8］黄春林，彭建设.双模量梁动力响应的时域GD法求解［J］.武汉理工大学学报（交通科学与工程版），2021，45（5）：945-949.

［9］陈廷兵，彭建设，林凡.解黏弹性地基梁受迫振动的时域DQ法［J］.成都大学学报（自然科学版），2018，37（1）：96-99.

（实习编辑：罗媛）