单相不间断电源逆变电路调制度对输出电压谐波的影响

严刚峰 吴保宁 柳恒敏

收稿日期：2023-05-03

基金项目：大型电气传动系统与装备技术国家重点实验室开放基金课题（ SKLLDJ022020003）；成都大学2022年实验教改项目（cdsyjg2022031）

作者简介：严刚峰（1977—），男，博士，副教授，从事单相不间断电源逆变电路控制、精密运动控制、嵌入式系统设计及控制系统建模等研究.Email：scuygf@163.com

摘要：详细分析单相不间断电源核心部分（逆变电路）的特点、类型、评价指标及控制方式，然后采用广泛应用的单相双极性正弦脉冲宽度调制法的全桥逆变电路作为研究对象，导出了逆变电路输出平均电压的表达式，采用仿真和理论相结合的方法讨论了频率调制度和幅值调制度的典型取值对输出电压谐波的影响.讨论结果表明，当载波频率为调制波频率的奇数倍时，取幅值调制度r=0.9左右，而当载波频率为调制波频率的偶数倍时，取幅值调制度r=0.5左右，此时输出逆变电压波形质量更好，谐波含量较小，对于改善逆变电路的设计和参数选择具有一定的参考价值.

关键词：不间断电源；全桥；逆变电路；调制度；谐波失真

中图分类号：TM464

文献标志码：A

0引言

单相不间断电源广泛用于宽负载范围的用电设备中，以提供具有较小总谐波失真的恒定正弦输出电压供电，在断电时可以立即投入使用，为关键设备在供电故障时连续可靠运行提供了保证［1］.单相不间断电源装置的核心是电力电子技术中的逆变器.逆变器是将直流电转换为交流电的逆变电路.由于逆变器的主要目标是使用直流电压源为需要交流的负载供电，因此讨论交流输出的质量非常重要.逆变器的输入取自各种直流电源，如化学电池、光伏电池、燃料电池及发电机等.单相逆变电路中使用的电路主要有半桥逆变电路和全桥逆变电路.单相半桥逆变电路由2个功率开关组成，其中，2个二极管与电源开关并联，以阻断反向电压，且开关的操作不会同时导通，若2个开关同时导通，由于电流很大，对功率开关会造成非常有害的影响.全桥逆变电路由4个功率开关组成，可以用于更高额定功率的场合，因此全桥逆变电路更为常用.对于提高供电质量，单相不间断电源也成了电力设备的首选.为了能够使单相不间断电源可靠且高质量地稳定运行，对于特定的用电需求，可以采用相应的逆变器控制方案来满足用户供电装置的指标要求.对于高性能单相不间断电源逆变器，指标要求更加严格，例如，对负载和输入电压变化的快速响应及非线性负载情况下要保持高质量输出电压的能力等.如果负载电流视为扰动，则单相不间断电源逆变器可被视为具有周期扰动的线性系统.线性和非线性控制器都可以应用于单相不间断电源逆变器的控制.单相不间断电源逆变器的控制问题可以视为具有周期扰动的线性系统的跟踪控制问题.此外，电力电子设备通常含有噪声，而且不容易获得逆变器模型的准确参数［2-4］.因此，单相不间断电源逆变器控制系统具有一定程度的鲁棒性是必要的，并且有潜力的单相不间断电源逆变器控制器应具有跟踪能力和鲁棒能力.

现有的大量研究集中在逆变器的控制方法［5］上.总体而言，控制方法分为3类：重复控制器［6-9］、非线性控制器［10-13］和基于模型的反馈控制器［14-16］.重复控制器可以有效地抑制周期性干扰，对系统参数的依赖性较小，但是动态性能较差，对非周期性干扰的抑制能力较弱.非线性控制器，比如滑模控制器、模糊控制器及人工神经网络控制器等，均能提高系统的动态性能，减小输出电压波形中的过冲量，但同时极大增加了控制器的复杂程度，且这些方法对参数失配非常敏感，将造成整个控制系统过于复杂且可靠性降低.基于模型的瞬时反馈控制器提供了适当的动态性能及有限稳态误差，但控制性能取决于系统结构参数的准确程度，由于在交流输出下控制系统回路的增益有限，因此稳态误差是无法完全消除的.

尽管存在大量的控制技术研究用于减小逆变器的输出电压谐波，但对于逆变电路自身结构所导致输出电压谐波影响的研究相对较少，因此，本研究采用广泛使用的三角载波正弦脉冲宽度调制的单相双极性全桥同步逆变电路为研究对象，推导了输出平均电压的表达式，采用仿真方法，重点分析了频率调制度和幅值调制度对输出脉冲谐波的影响，为设计逆变电路及提高逆变电路输出波形的控制效果提供参考.

1单相双极性全桥同步逆变电路

大多数单相不间断电源逆变器都采用了晶体管作为功率开关器件，并且主要为电压源逆变器类型，且由直流电路向逆变桥提供直流电压源.单相逆变桥主要有2种典型设计，即全桥逆变电路和半桥逆变电路.采用此2种逆变电路设计的逆变器可以使用类似的方式建模，也可以对2种类型的逆变器使用相同的控制方法.这些逆变器将全桥或半桥的输出通过电感电容滤波器来产生平滑的正弦逆变输出电压用于供电.逆变桥通常以远高于输出电压基波的开关频率进行脉冲宽度调制，以使滤波器组件的大小与额定值降至最低.对于单相不间断电源逆变器输出电压的要求主要包括：在逆变电路的单一参数变化情况下，比如负载电流、温度或直流电压源等参数单独变化时，输出交流电压的稳态有效值应保持在±2%额定值以内；当100%额定负载加到单相不间断电源输出端或从其输出端移除时，瞬时电压峰值的偏差应在10%额定值幅度以内.负载变化后输出电压的稳定时间小于0.04 s，输出电压瞬时值应在额定值的5%以内.对于不同额定功率以内的线性负载或非线性负载接入逆变器输出时，逆变器产生的最大总谐波失真不能超过4%.单相不间断电源逆变器输出电压的指标要求中，输出电压波形的质量，即最大总谐波失真的指标，最为重要.

现代逆变器均采用脉冲宽度调制来控制和实现期望的电压输出.脉冲宽度调制是通过调制占空比来调制脉冲持续时间，从而产生等幅脉冲的技术.模拟脉冲宽度调制控制需要生成输入比较器的参考信号和载波信号，并基于开关逻辑输出生成最终的控制信号.参考信号是所期望的信号输出，可能是正弦波或方波，而载波信号一般是锯齿波或三角波，其频率一般都会大大高于参考信号的频率.众多工业应用中，通常需要控制逆变器输出电压变化的原因包括应对直流输入电压的变化、用于逆变器的输出电压调节及对于恒压/频率控制的需求.控制增益或输出电压的最有效方法是在逆变器中采用脉冲宽度调制控制.常用的脉冲宽度调制技术有线性调制、锯齿波脉冲宽度调制、单脉冲宽度调制、多脉冲宽度调制及正弦波脉冲宽度调制.

正弦波脉冲宽度调制不像多脉冲宽度调制那样保持所有脉冲的宽度相同，而是每个脉冲的宽度与在相同脉冲中心的正弦波振幅成比例变化.这种调制方式使输出电压的失真度和低次谐波都有显著降低.将正弦参考信号与高频率的三角波载波进行比较，从而生成选通信号.参考信号的频率决定逆变器的输出频率及输出电压峰值的幅度，也可以调整频率调制率及输出电压.每个控制周期的脉冲数取决于载波频率的大小.

由于使用脉冲宽度调制开关技术的逆变器的输入通常是具有幅值恒定的直流输入电压，因而逆变器的工作就是获取这个输入电压，然后由控制电路来输出期望的交流电压，其中幅度和频率均可以控制，且有许多不同的方法可以实现脉冲宽度调制以将输出整形为交流电源.为了输出特定频率的正弦波形，正弦波脉冲宽度调制技术将特定频率的正弦控制信号与三角波形进行比较，然后逆变器使用三角波的频率作为开关频率，且作为载波的三角波频率通常保持不变.三角波的频率决定了逆变电路开关的关闭和打开的速度.控制信号用于调制开关占空比，根据“脉冲等效原理”来输出要求的波形，以决定输出电压的频率和幅值.此时，输出电压除了含有逆变电路控制信号的基波及其谐波外，由于逆变电路的输出还要受开关频率的影响，因此逆变电路输出电压还将包含开关频率的谐波，且这类谐波一般是高频的.因此，逆变电路输出电压波形的质量，即输出电压的畸变主要由频率调制度及幅值调制度决定.

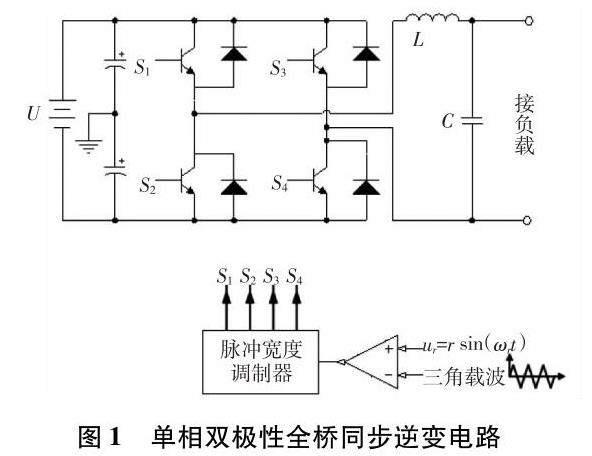
下面根据广泛采用的单相双极性全桥同步正弦波脉冲宽度调制逆变电路来分析其输出电压波形的质量.具体电路如图1所示，输出波形如图2所示.

正弦波脉冲宽度调制双极性方式在输出电压的整个周期内，三角波载波是双极性的，有正有负，所得脉冲宽度调制波也是有正有负的.在输出电压的1个周期内，输出的脉冲宽度调制波只有±U此2种电平.在调制波ur和三角载波信号uc的交点时刻控制开关器件S1、S2、S3、S4的通断，且在ur的正、负半周，对各开关器件的控制规律为：当ur>uc时，给S1和S4 以导通信号，给S2和S3以关断信号，此时输出电压为U；当ur

2单相双极性全桥同步逆变电路输出电压的特征

2.1输出平均电压

取等腰三角载波信号的幅值为1，频率为fc，调制波ur=rsin（ωrt），其中r为幅值调制度.根据市电为50 Hz的电压频率，取ωr=100π（单位：rad/s），此处考虑r的取值范围是r∈（0，1.2］，即考虑过调制情形.

首先导出输出的平均电压，如图2所示.取三角载波从-1开始的1个周期，即时刻t2、t3所在周期来计算输出平均电压值.根据几何关系得出，

t2=14Tcrsin（ωrt2）+1+34Tc（1）

式中，Tc=1/fc为三角载波信号的周期.

t3=14Tc3－rsin（ωrt3）+34Tc（2）

所以，在此三角载波信号周期内输出电压的平均值为，

urmean=1TcTc－（t3－t2）U－（t3－t2）U=rUsin（ωrt3）+sin（ωrt2）=2rUsin（t3+t22ωr）cos（t3－t22ωr）（3）

式中，U为逆变器直流供电电压.考虑到频率调制度Mf=（fr/fc）1，所以，t3≈t2，urmean≈2rUsin（ωrt2）.因此，逆变器输出的瞬时平均电压与调制波ur=rsin（ωrt）频率相同，按正弦函数变化，按照冲量等效原理实现理想的正弦波逆变输出的功能，此处不考虑硬件的实现难度及开关次数导致的损耗.由此可知，三角载波的频率越高，这种近似的效果就越好.

2.2输出电压谐波分析

输出电压信号的傅里叶级数展开可记为，

uo（t）=a02+∑∞n=1ancos（nωrt）+bnsin（nωrt）（4）

式中，an=2Tr∫Tr0uo（t）cos（nωrt）dt，bn=2Tr∫Tr0uo（t）sin（nωrt）dt.

2.2.1频率调制度为奇数

从图2可知，当（fc/fr）=2k+1且k∈N+时，输出电压uo（t）波形的正半周期与负半周期是形状完全相同且符号相反的脉冲序列.此时，

uo（t）=∑∞n=2l+1bnsin（nωrt），l∈N+（5）

采用载波频率为50 Hz且频率调制度为奇数时，输出电压的谐波含量如图3所示.

从输出电压的幅频特性可知，输出电压仅含有奇次谐波，这和式（5）是一致的.从谐波含量来看，3次谐波的幅值相对较小，5次谐波的幅值增加较快，随后的奇次谐波逐渐减小.

uo（t）基波的均方根值可以与没有脉冲宽度调制时获得的电压基波均方根值进行比较，以确定电压损失.此时，输出电压uo（t）基波分量的均方根值为Uo1=（U/2），而没有脉冲宽度调制时获得的电压基波均方根值为（22U/π），由此得到电压利用率为（U/2）÷（22U/π）=78.5%，因此输出电压的损失为21.5%.

2.2.2频率调制度为偶数

当（fc/fr）=2k且k∈N+时，输出电压如图4所示.输出电压uo（t）含有直流分量，此时，

uo（t）=a02+∑∞n=1ancos（nωrt）（6）从输出电压的幅频特性可知，输出电压含有调制波整数倍的各次谐波，这和式（6）是一致的.从谐波含量来看，4次谐波的幅值较大，其他各次谐波的幅值大小没有确定的规律.

类似于频率调制度为奇数时的分析，此时输出电压的损失仍保持为21.5%.

因此，设计逆变电路中，当选择三角载波信号频率是调制波频率的偶数倍同步调制时，输出电压不仅含有直流分量，同时也含有调制波频率的整数倍谐波，而当选择三角载波信号频率是调制波频率的奇数倍同步调制时，则输出电压仅含有调制波频率的奇数倍谐波，这将有利于后续滤波电路的设计且减小输出电压的总谐波失真.但针对仅电压损失的情况，二者有相同的结果.

2.3幅值调制度对输出电压总谐波失真的影响

为了讨论幅值调制度的取值对单相双极性正弦波脉冲宽度调制全桥同步逆变电路输出电压总谐波失真的影响，构建如图6所示的仿真原理图进行仿真.图6中，单相双极性正弦波脉冲宽度调制全桥同步逆变仿真电路由2个桥臂组成，每个桥臂上都有2个由Simulink软件提供的模拟晶体管开关，每个模拟晶体管开关上都接有反向的续流二极管，用于反向电流的放电.在常见的阻感负载情况下，反向负载电流流经这些续流二极管，为在关断条件下的感应电流提供流通的路径.模拟晶体管开关组S1和S4与S2和S3在比较器的输出控制下，成对地交替工作以获得交流输出.载波采用三角波.三角波由Simulink软件提供的相应模块产生，可以生成理想的精密三角波，其频率为1 KHz，幅值为1 V.如图7所示，调制波为正弦波，其波形为ur=rsin（100πt），也由Simulink软件中的相应模块直接产生.

考虑到高次谐波容易被后续滤波器滤除，这里定义总谐波失真（tutal harmonic distortion，THD）为，

THD=∑8i=2UiU12（7）

式中，Ui为i次输出电压谐波的有效值，U1为输出电压基波的有效值.

分别取调制波频率为载波频率奇数倍和偶数倍时，固定三角载波信号幅值，增加调制波ur=rsin（100πt）的幅值从r=0.1增加至r=1.2，所得相对于基波的总谐波失真如图8所示.

由图8可知，当调制波频率为载波频率奇数倍时，总体上谐波失真小于同幅值调制度时调制波频率为载波频率偶数倍的情形.当r取0.9左右，总谐波失真较小.当调制波频率为载波频率偶数倍且r取0.5左右时，总谐波失真较小.当处于幅值过调制时（r>1），2种情形下的总谐波失真都会迅速增加.

3结论

对于广泛使用的三角载波正弦脉冲宽度调制的单相双极性全桥同步逆变电路，若不考虑设备硬件的实现难度，当三角载波的频率越高，正弦波输出的近似效果越好.选择调制波频率是三角载波频率的奇数倍同步调制时，有助于提高正弦波输出波形，减小谐波输出分量.当调制波频率为载波频率奇数倍且取r=0.9左右或调制波频率为载波频率偶数倍且取r=0.5左右时，输出逆变电压的谐波失真均较小，有利于后续滤波电路的设计，对于改善逆变器的设计具有一定的参考价值.本研究不足之处在于未考虑开关器件导通时死区时间的影响，只是从输出电压波形谐波抑制的角度及电压损失的角度进行了分析.下一步的研究重点将是开关器件导通时死区时间的影响.

参考文献：

［1］薛家祥，陈永煌，沙幸威.UPS电源中单相PWM整流器双闭环控制策略［J］.自动化与仪表，2017，32（7）：72-76.

［2］Seyedalipour S S，Shahparasti M，Hajizadeh A，et al.Modelbased control of fourleg inverter for UPS applications considering the effect of neutral line inductor［J］.IET Power Electr，2021，14（8）：1468-1479.

［3］Blachuta M，Bieda R，Grygiel R.High performance single and double loop digital and hybrid PIDtype control for DC/AC voltage source inverters［J］.Energies，2022，15（1）：1-25.

［4］Kabalc E.Multilevel inverters［M］.New York，NY，USA：Academic Press，2021：1-27.

［5］Oliveira T.Model predictive control for paralleled uninterruptible power supplies with an additional inverter leg for loadside neutral connection［J］.Energies，2021，14（1）：1-29.

［6］梁欢，张琦，唐雨，等.用于并网逆变器谐波抑制的重复控制策略研究［J］.电力电子技术，2022，56（9）：5-7.

［7］李冬辉，孔祥洁，刘玲玲.单相双Buck逆变器的无差拍快速重复控制［J］.电网技术，2019，43（10）：3671-3677.

［8］贾要勤，朱明琳，凤勇.基于状态反馈的单相电压型逆变器重复控制［J］.电工技术学报，2014，29（6）：57-63.

［9］张坤，罗文广.电压型逆变器的重复控制与准比例谐振的双闭环控制研究［J］.广西科技大学学报，2022，33（3）：22-28.

［10］王锦博，董锋斌，荔凡凡，等.单相全桥电压型逆变器的负载电流前馈控制策略［J］.电工技术，2019（23）：16-18.

［11］侯波，穆安乐，董锋斌，等.单相电压型全桥逆变器的反步滑模控制策略［J］.电工技术学报，2015，30（20）：93-99.

［12］游国栋，李继生，侯勇，等.单相光伏并网逆变器的反步滑模控制策略［J］.电网技术，2015，39（4）：916-923.

［13］卢伟国，栗安鑫，赵乃宽，等.改进的Lyapunov直接法控制单相Buck型逆变器［J］.电机与控制学报，2014，18（7）：18-23.

［14］张颖，雷鸣宇，王一波，等.自适应连续集模型预测控制在逆变器上的应用［J］.电力电子技术，2022，56（10）：49-52.

［15］袁绍军，郭金智，尹兆磊，等.单相逆变器双环+时滞的复合控制方法研究［J］.电力电子技术，2022，56（8）：32-35.

［16］高兰香，赵兴勇，宋玲燕，等.基于滑模控制的光伏并网逆变器控制策略［J］.自动化与仪表，2022，37（11）：37-43.

（实习编辑：黄爱明）