基于实测位移的水下大直径盾构隧道外荷载反演研究

陈稳 鲁志鹏 吴鑫林 郭志华

摘 要：【目的】為了实现水下盾构隧道整断面结构力学状态的长久监测。【方法】依托江苏某过江大直径盾构隧道工程，利用ATS激光跟踪的盾构隧道管片变形高精度测量与数据预处理方法，基于变形实测数据，结合遗传算法和阻尼最小二乘法优化方法，对盾构隧道横断面外部荷载状况进行反演，并与监测结果进行对比分析。【结果】工程应用表明：通过遗传算法与阻尼最小二乘法所反演的外部荷载数值均介于现场实测与太沙基理论之间。与两者相比，水平荷载最小误差为1%，最大误差为13.54%，平均误差为5.98%；顶部竖向荷载最小误差为6.11%，最大误差为13.2%，平均误差为10.47%。【结论】基于现场实测位移数据，反演水下盾构隧道任意断面、任意时间段的外部荷载状况的技术路线是可行的，为隧道外荷载状态及时监测提供了一种新途径。

关键词：水下盾构隧道；精密测量；遗传算法；阻尼最小二乘法；荷载

中图分类号：U456.3      文献标志码：A    文章编号：1003-5168（2024）07-0075-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.07.015

Research on External Load Inversion of Underwater Large-Diameter Shield Tunnel Based on Measured Displacement

CHEN Wen1 LU Zhipeng2 WU Xinlin2  GUO Zhihua3，4

（1.Jiangsu Construction Bureau of Transportation Engineering， Nanjing 210004，China;

2.China Railway Siyuan Survey and Design Institute Group Co.， Ltd.， Wuhan 430063，China;

3. Shanghai Tongyan Civil Engineering Technology Co.， Ltd.， Shanghai 200092，China;

4. Shanghai Engineering Research Center of Detecting Equipment for Underground Infrastructure， Shanghai 200092，China）

Abstract： [Purposes] This paper aims to reflect the structural mechanics state of the whole section of underwater shield tunnel permanently and accurately. [Methods] Based on a large-diameter shield tunnel project across the river in Jiangsu Province， the high-precision measurement and data preprocessing method of shield tunnel segment deformation based on ATS laser tracking is used. Based on the measured deformation data and combined with genetic algorithm and damping least squares optimization method， the external load condition of shield tunnel cross section is inverted， and  the results were compared with the monitoring results.[Findings] Engineering applications show that： The external loads inverted by genetic algorithm and damped least square method are between the field measurement and Terzaghi theory. Compared with the two， the minimum error of horizontal load is 1%， the maximum error is 13.54%， and the average error is 5.98%. The minimum error of the vertical load at the top is 6.11%， the maximum error is 13.2%， and the average error is 10.47%.[Conclusions] Based on the field measured displacement data， the technical route of inverting the external load condition of underwater shield tunnel at any section and any time period is feasible， which provides a new way for the timely monitoring of the external load condition of the tunnel.

Keywords： underwater shield tunnel; precise measurement; genetic algorithm; damped least square method; load

0 引言

我国海湾海峡、内陆江河都较为发达，为促进区域协调发展，各种跨海越江通道应运而生，其中盾构隧道凭借其施工速度快、适应性好等特点，在跨海越江通道工程中得到了广泛应用。水下盾构隧道地质条件复杂、承受高水压、结构受力变形大，给隧道结构安全带来巨大的挑战［1-2］。因此，需要对隧道结构进行长期监测，以评估隧道荷载和结构安全状态。

目前，水下盾构隧道结构主要通过在预设断面内预埋传感器进行监测［3-5］。但工程经验表明，随着施工推进及后期运营，发现预埋传感器易损坏，且预设监测断面并非与重点监测断面一致，后期重点监测断面也无法预埋传感器，难以为运营期隧道结构安全评价提供“零状态”的基础数据。

为解决上述难题，众多学者尝试利用实测位移或内力进行盾构隧道结构状态的反演分析进行研究［6］。周济民等［7］通过引入正交试验法，考虑不同的荷载系数，反演分析黄土地层隧道管片衬砌结构荷载设计值。钟小春等［8］基于现场测量内力信息，应用复合形法分别反演深埋和浅埋条件下，衬砌结构上土压力的大小和分布方式。李策等［9］基于武汉地铁8号线现场监测数据，通过全面试验的方法反演隧道荷载。封坤等［10］基于遗传算法和健康监测数据，反演水下全断面砂岩盾构隧道的水土荷载，为类似隧道设计提供安全支撑。

现有研究多根据现场应力数据开展，对基于位移信息反演隧道外荷载的研究较少。隧道现场位移信息相对于应力信息较易获得，并且不一定依赖预埋传感器。因此，本研究基于现场实测位移数据，反演隧道结构荷载，并与结构监测数据进行对比，分析隧道结构变形与受力特征，从而提出一种评估任意断面、任意时间段水下盾构隧道结构外荷载的方法。

1 盾构隧道结构外荷载反演研究

1.1 研究思路

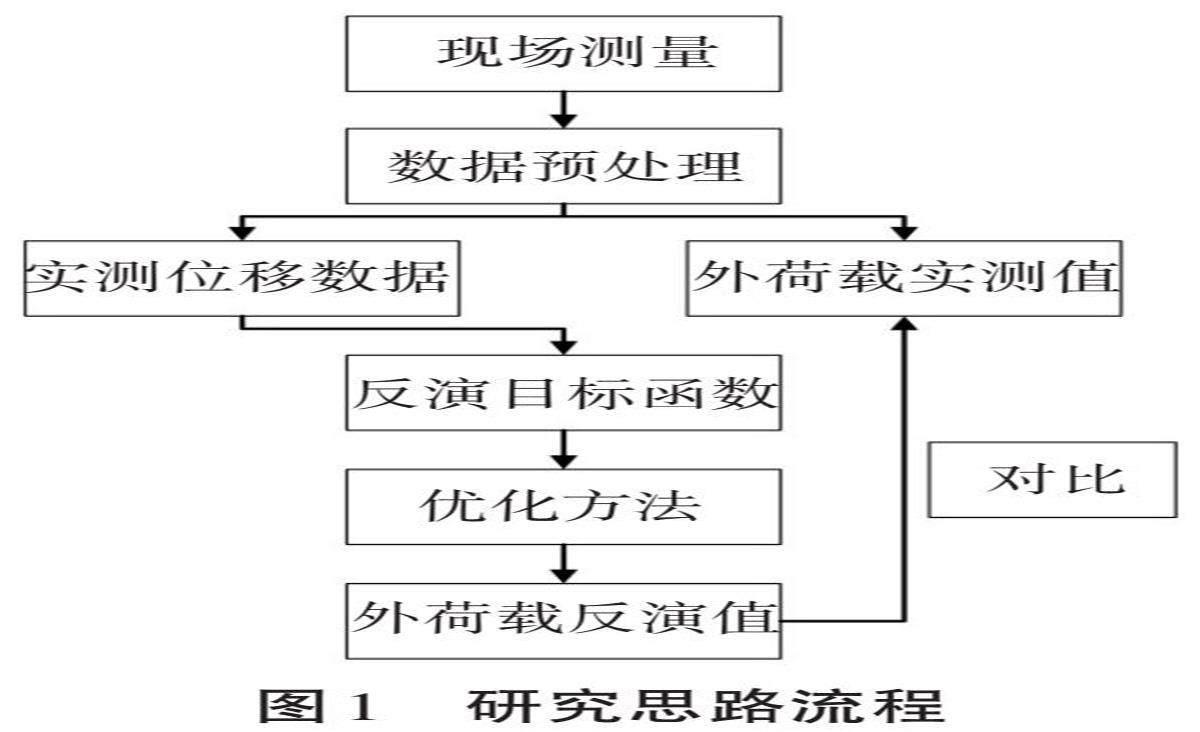
首先，构建ATS激光跟踪［11］的盾构隧道管片变形高精度测量与数据预处理方法，获得现场实测位移数据。其次，建立反演目标函数，采用不同優化方法，反演隧道结构外荷载。最后，将反演值与实际监测值进行对比，验证研究的正确性，研究思路流程如图1所示。

1.2 盾构管片变形精密测量

为了获得盾构管片的变形情况，可比较管片弦长变化量。如图2所示，将管片弦长由上到下分成3条测线，测点1、测点4分别是管片两端上的测点，则管片弦长L的计算公式见式（1）。

[L=（X1-X4）2+（Y1-Y4）2+（Z1-Z4）2] （1）

式中：测点1坐标（X1，Y1，Z1），测点4坐标（X4，Y4，Z4）。

分别按照式（1）对不同监测周期的3条测线进行计算并取平均值，可获得管片弦长L变化量[δc]，见式（2）。

[δc=ΔL=L-L'] （2）

式中：[L]、[L']分别为不同期管片弦长L监测结果的平均值。

1.3 反演分析方法

1.3.1 反演思路。反演分析的本质是非线性问题的全局最优解搜索，即通过若干已知点的测量数据求解多个参数的最优组合的过程，随着反演参数的增多，全局最优解的获得也就越复杂。通过不同的优化方法，每次对多参数进行优化重组，并采用有限元方法计算该种参数组合下的位移值，代入目标函数进行迭代，获得最优参数组合。位移反演分析目标函数见式（3）。

[F（x）=i=1nf2i（x）=][i=1n（δi-δ*i）2] （3）

式中：[δ*i]为现场量测位移值；[δi]为反分析计算位移值；[n]为测线条数。

反演分析包括建立隧道模型、输入位移测线、设置边界条件、选择反演方法，以及在设置反演参数后进行有限元计算。当目标函数小于控制值时，输出反演参数值，具体的流程如图3所示。

1.3.2 优化方法。常见的优化方法有遗传算法、阻尼最小二乘法等，本研究将分别使用这两种方法反演隧道外部荷载。

①遗传算法。遗传算法（Genetic Algorithm，GA）［12］，是美国科学家于二十世纪七十年代提出的模拟达尔文生物自然进化过程，采用概率化寻找最优解的方法。遗传算法的具体计算流程如图4所示，包括反演参数编码、初始种群、个体适应度计算、遗传操作和迭代终止条件等步骤［13］。

编码是用某种方式的符号串表示具体的反演参数。对于非线性问题，通常采用二进制编码方式解决。二进制编码规则见式（4）。

[ε≥（bi-ai）（2l+1）] （4）

式中：[ε]为参数编码精度；[xi∈[ai，bi]]为待识别参数的[xi]的取值范围；l为二进制编码长度。

子串解码见式（5）。

[xi=ai+εj=1lgj2j-1] （5）

式中：[gi]为染色体串第[j]位的值，[gj=0，1]。

初始种群一般由随机法形成，使其尽可能均匀分布于整个解空间上。遗传操作包括选择、交叉和变异。算法根据个体适应度好坏进行选择操作。个体适应度指的是个体在种群生存的优势程度度量，适应度越大代表该个体越优，有很大的可能性遗传到下一代个体。对于遗传算法，由于反演目标函数值较小，更易求目标函数的最大值。因此，个体适应度应采用目标函数的倒数计算，见式（6）。

[φx=1i=1nδi-δ*i2] （6）

交叉是通过某一概率交换父代的部分染色体，从而形成新的个体。变异的主要作用是使种群产生新的个体，以提高种群的多样性。

②阻尼最小二乘法。阻尼最小二乘法［14］是对最小二乘法的改进，该方法的优越性体现于阻尼因子的调节作用。该方法既兼具了最速下降法在远离最优解时保证迭代收敛的特性，又继承了高斯牛顿法在接近最优解时高效的收敛速度，兼具了高斯－牛顿法和最速下降法的优点，算法的主要步骤如下。

假设[X=[x1，x2，…，xm]T]，[m]为参数个数。则目标函数改写为式（7）。

[minF（x）=minfT（x）f（x）=min||f（x）||2] （7）

上述目标函数可归纳为最小二乘问题，其主要迭代公式可写为式（8）。

[Hxδx=gx] （8）

式中：H（x）称为海瑟矩阵，δx为待求的搜索方向；g（x）为右侧项。

对上式增加步长因子[μ]和阻尼因子[α]，阻尼最小二乘法的迭代公式见式（9），推导过程参考文献［15］。

[（JTkJk+μI）αδx=-JTkF（x）] （9）

式中：[Jk=?f1（xk）T??fm（xk）T][=?f1（xk）?x1…?f1（xk）?xn????fm（xk）?x1…?fm（xk）?xn]；[I]为[n]阶单位矩阵。

1.4 位移数据预处理

由于实际工程中位移信息以弦长测线形式组织，需要将有限元节点位移与实测位移测线对应起来，转换方法如下：①选取实测位移测线，以测点i为起点、j为终点，构建测线向量[ij]；②将测点作为约束点进行网格剖分，测点与有限元结点严格对应，并计算测点对应的有限元节点在x、y方向上的位移及位移矢量[ii']、[jj']，如图5（a）所示；③位移矢量向测线向量上投影，得到位移矢量[ii']、[jj']在测线向量[ij]上的位移值[δii'c]、[δjj'c]，如图5（b）所示；④以i点为基点，则节点i、j的测线变化量为[δ=δjj'c-δii'c]，其中，正值表示拉伸，负值表示压缩；⑤节点间相对位移[δ]与实测测线收敛位移[δc]的差值平方[Δδ=（δ-δc）2]为误差控制值。

2 软件开发与工程应用

2.1 软件开发

基于上述研究成果，本研究利用同济曙光数值分析平台（TJSG），开发了盾构隧道结构位移反演分析软件。软件通过对该隧道断面参数化建模，并输入现场实测变形数据，设置优化算法的控制参数，从而对隧道外部荷载进行反演分析。

2.2 工程應用

2.2.1 工程概况。江苏某过江隧道项目路线全长约11.825 km，隧道段 6.445 km，隧道分为右线和左线，其中盾构段右线长约4 952 m，左线长约4 937 m。该工程为大直径高水压盾构隧道，盾构断面外径15.50 m、内径14.20 m，管片厚度0.65 m。分块形式为1块封顶环、2块衔接环、7块标准环。隧道下穿长江深槽段，整体结构承受超大的水土压力。通过选取右线隧道里程YK3+735作为监测断面，发现该测试断面埋深18.91 m，地下水位距断面顶部17.62 m，断面主要穿越粉质黏土层，具体地质剖面情况如图6所示。

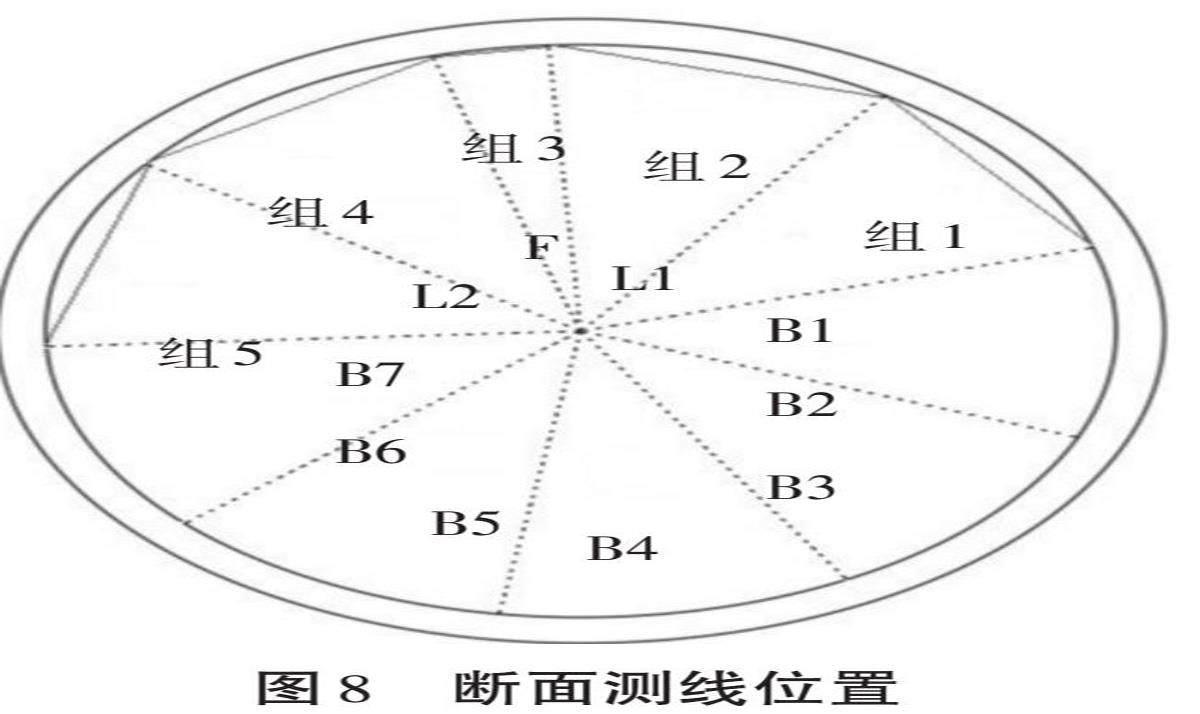
2.2.2 断面荷载与变形。工程采用光纤光栅土压力盒和光纤光栅渗压力计对YK3+735断面水土荷载进行监测，分别布置在F、L1、B1、B2、B3、B4、B5、B6、B7和L2管片外部，每处均埋设一个土压力盒和渗压力计，共10组。传感器位置如图7所示。

隧道断面穿越地层为粉质黏土层，外部荷载采用水土合算进行计算，主要考虑以下荷载：顶部水土压力Q1、水平水土压力P1和P2、管片自重、竖向荷载反力Q3和地基抗力。

结合断面水土压力计位置，得出现场实测水土压力值。采用太沙基理论计算断面水土荷载，与实测数据相比，太沙基理论所计算出的顶部水土荷载Q1为337.3 kPa，水平荷载P1为138.5 kPa，水平荷载P2为213.6 kPa，考虑到现场注浆压力等因素的作用，太沙基理论计算的外部荷载均明显小于现场实测值，结果见表1。

2.2.3 基于现场实测位移反演隧道外部荷载。将精密测量的管片变形数据作为反演的相对位移测线，输入盾构隧道结构位移反演反分析软件，分别采用遗传算法和阻尼最小二乘法，反演隧道断面外部水土荷载。反演荷载包括顶部竖向荷载Q1、顶部水平荷载P1、底部水平荷载P2。遗传算法的种群规模设置为20，变异概率为0.1。反演过程中，适应度变化曲线如图9所示。随迭代代数的增加，适应度逐渐变大，到第13代时适应度变化达到稳定状态。阻尼最小二乘法的差分步长设置为0.01。反演迭代过程如图10所示，随着迭代次数的增加，目标函数的残差平方和逐渐减小，到第3代残差平方和达到相对稳定状态。

遗传算法和阻尼最小二乘法反演隧道外部荷载结果见表3。遗传算法选择第13代荷载结果，隧道断面竖向荷载Q1为382.13 kPa，水平荷载P1为147.11 kPa，水平荷载P2为211.59 kPa。阻尼最小二乘法选择第3代反演结果，隧道断面竖向荷载为375.86 kPa，水平荷载P1为135.48 kPa，水平荷载P2为218.69 kPa。

与现场实测结果相比，遗传算法反演竖向荷载的误差为11.17%，水平荷载P1的误差为6.11%，水平荷载P2的误差为9.8%。阻尼最小二乘法反演竖向荷载的误差为12.63%，水平荷载P1的误差为13.54%，水平荷载P2的误差为6.78%。

与太沙基理论相比，遗传算法与阻尼最小二乘法反演竖向荷载的误差分别是13.2%和11.4%，水平荷载P1的误差分别是6.21%和2.1%，水平荷载P2的误差分别是1%和2.3%，具体反演误差如图11所示。研究发现，两种方法对顶部水土荷载的反演误差较高，遗传算法与阻尼最小二乘法所计算的数值均介于现场实测与太沙基理论之间，与两者相比计算的误差均小于15%，能有效地反映隧道断面外部荷载的真实情况，也说明了该方法的正确性。

3 结论

①构建ATS激光跟踪的盾构隧道管片变形高精度测量与数据预处理方法，距离测量精度可达0.01 mm，可满足隧道结构基于实测位移反演分析需求。

②遗传算法与阻尼最小二乘法所反演的数值介于现场实测与太沙基理论之间。与两者相比，水平荷载均误差为5.98%，顶部竖向荷载均误差为10.47%，荷载反演准确度较高，可满足工程评价要求。

③基于实际监测的位移数据，通过反演方法评估水下盾构隧道任意断面、任意时间段外部荷载状况的技术路线是可行的，可为隧道外荷载状态及时监测提供了一种新途径。后续应进一步开展基于实测位移的水下大直径盾构隧道结构材料、内力等参数的反演研究，并推广应用于地铁、铁路及公路隧道监测等领域。

参考文献：

［1］TAN X Y，CHEN W Z，WU G J，et al. A structural health monitoring system for data analysis of segment joint opening in an underwater shield tunnel［J］. Structural Health Monitoring，2020，19（4）：1032-1050.

［2］李长俊，陈卫忠，杨建平，等. 运营期水下盾构隧道管片接缝张开度变化规律［J］. 岩土力学，2018，39（10）：3783-3793.

［3］王军，张巍.南京长江隧道管片结构健康监测系统设计与应用［J］.地下工程与隧道，2009（3）：5-13.

［4］刘胜春，张顶力，黄俊，等.大型盾构隧道结构健康监测系统设计研究［J］.地下空间与工程学报，2011，7（4）：741-748.

［5］孙可，张巍，朱守兵，等.盾构隧道健康监测数据的模糊层次分析综合评价方法［J］.防灾减灾工程学报，2015，35（6）：769-776.

［6］邓之友.浅埋偏压隧道结构荷载反分析研究［D］.长沙：中南大学，2012.

［7］周济民，何川，方勇，等.黄土地层盾构隧道受力监测与荷载作用模式的反演分析［J］.岩土力学，2011，32（1）：165-171.

［8］钟小春，朱伟.盾构衬砌管片土压力反分析研究［J］.岩土力学，2006（10）：1743-1748.

［9］李策，王士民，王承震，等.基于实测内力的大直径水下盾构隧道荷载反演分析［J］.土木工程学报，2020，53（3）：103-113.

［10］封坤，李茂然，曹翔鹏，等.基于遗传算法的水下全断面砂岩盾构隧道荷载反演分析［J］.铁道标准设计，2023，67（4）：107-115.

［11］范百兴，李广云，易旺民，等.激光跟踪仪测量原理与应用［M］.北京：测绘出版社，2017.

［12］KENETH A D J. An analysis of the behavior of a class of genetic adaptive systems［D］. Michigan ：University of Michigan ，1975.

［13］薛光橋，程岩，刘笑娣，等.基于遗传算法的盾构隧道管片接头刚度反演研究［J］.现代隧道技术，2022，59（2）：78-85.

［14］肖艳丽，李明星.阻尼最小二乘算法研究综述［J］.软件导刊，2018，17（8）：9-12.

［15］王哲成，秦祯秋，刘笑娣，等.基于阻尼最小二乘法的盾构隧道围岩力学参数反演［J］.地下空间与工程学报，2023，19（3）：737-749.

收稿日期：2023-08-21

作者简介：陈稳（1996—），男，硕士，助理工程师，研究方向：高速公路及过江通道建设管理。

通信作者：郭志华（1996—），男，硕士，助理工程师，研究方向：岩土数值分析。