复杂地质条件下浅海区电性源瞬变电磁法三维响应特征

雷松达 王显祥 刘遂明

雷松達，王显祥，刘遂明. 复杂地质条件下浅海区电性源瞬变电磁法三维响应特征. 吉林大学学报（地球科学版），2024，54（3）：10161030. doi：10.13278/j.cnki.jjuese.20230336.

Lei Songda， Wang Xianxiang， Liu Suiming. Three-Dimensional Response Characteristics of Transient Electromagnetic Method with Electrical Sources in Shallow Sea Areas Under Complex Geological Conditions. Journal of Jilin University （Earth Science Edition）， 2024， 54 （3）： 10161030. doi：10.13278/j.cnki.jjuese.20230336.

摘要：

与频域电磁法相比，瞬变电磁法可有效区分空气波和海底电磁响应，在浅海油气藏探测中具有良好的应用前景。近海海域地质条件一般较为复杂，普遍具有强切割地形及复杂构造，使电磁场响应特征变得异常复杂，给数据解释工作带来极大困难。本文基于时域有限元法，采用非结构化网格对复杂地质模型进行剖分，通过构建时域有限元方程并结合偶极子离散的长导线源近似技术以及后退欧拉离散技术，实现了复杂地质条件下浅海区电性源瞬变电磁三维正演模拟。在验证算法精度后，通过复杂地质模型的三维正演，分析了不同海水深度对空气波与海底油气藏目标体的影响，在此基础上，进一步分析了不同围岩电阻率以及海底地形对油气藏目标体分辨率的影响，结果表明：在浅海条件下，脉冲响应受空气波影响较大，阶跃响应受空气波影响较小，随着深度增大空气波影响变小，对油气藏的分辨率也降低；围岩电阻率及海底复杂地形对电性源瞬变电磁影响严重。

关键词：

瞬变电磁法；浅海；非结构化网格；三维正演；时域有限元

doi：10.13278/j.cnki.jjuese.20230336

中图分类号：P631.3

文献标志码：A

收稿日期：20231208

作者简介：雷松达（1999—），男，硕士研究生，主要从事瞬变电磁法正反演方面的研究，E-mail：em_leisongda@163.com

通信作者：王显祥（1986—），男，副教授，博士，主要从事瞬变电磁法数值模拟及反演方面的研究，E-mail：wangxianxiang09@163.com

基金项目：国家自然科学基金项目（42274185，41964006）

Supported by the National Natural Science Foundation of China （42274185， 41964006）

Three-Dimensional Response Characteristics of Transient Electromagnetic Method with Electrical Sources in Shallow Sea Areas Under Complex Geological Conditions

Lei Songda， Wang Xianxiang， Liu Suiming

School of Geophysics and Measurement-Control Technology， East China University of Technology， Nanchang 330013， China

Abstract：

Compared with the frequency domain electromagnetic method， the transient electromagnetic method can effectively distinguish between  air waves and seafloor electromagnetic response， which has a good application prospect in the shallow offshore oil and gas reservoir detection. The geological conditions of offshore area are generally more complicated， and there are strong cut terrain and complex structures，  making the electromagnetic field response characteristics become extremely complex. These problems will bring great difficulties to the data interpretation work. In this paper， based on the time-domain finite element method （FEM）， the unstructured mesh is used to dissect the complex geological model. By constructing the time-domain finite element equations and combining the long wire source approximation technique with dipole discretization and the backward Euler discretization technique， the three-dimensional forward modeling  simulation of   electromagnetic transient with  electrical source in shallow sea  area under  complex geological conditions is realized. After verifying the accuracy of the algorithm， the influence of different seawater depths on  air waves and the target body of  seafloor  oil and gas reservoir is analyzed through the three-dimensional forward modeling  of the complex geological model. Based on these results， the influence of different surrounding rock resistivity and seafloor  topography on the resolution of the target body of  oil and gas reservoir is further analyzed.  The results show that under shallow sea conditions， the pulse response is greatly affected by air waves， while the step response is less affected by air waves. As the depth increases， the influence of air waves  decreases， and the resolution of oil and gas reservoirs also decreases. The electrical resistivity of surrounding rocks and the complex seafloor topopraphy  have a serious impact on the transient electromagnetic properties of electrical sources.

Key words：

transient electromagnetic method; shallow sea; unstructured grid; 3D forward modeling; time domain finite element

0  引言

海洋电磁法作为探测海底资源分布的重要地球物理方法之一，可有效弥补地震勘探在海底异常探测分辨率不足的问题［1］。国际上将水深500 m以内的海域定义为浅海区域。我国作为海洋大国，浅海区域面积占总海域的60％以上［2］，近海待发现油气资源量约占我国待发现资源量的2/3［3］。空气波对海洋电磁信号影响显著，影响范围和幅度随海水深度的减小而增大。与深海水域多用频域电磁法不同，浅海域较薄的海水层使频域电磁场受空气波干扰严重，而瞬变电磁法可以有效区分空气波与海底地层的响应，在浅海资源勘探中具有更高的分辨率［45］。瞬变电磁法按照发射源方式可分为磁性源和电性源，其中：磁性源以不接地线圈作为发射源，通过接收线圈进行观测，由于发射线圈所产生的磁场信号在地层中衰减较快，探测深度较浅［67］；电性源利用接地长导线作为发射源，对高阻体的可分辨厚度大幅提升至埋深的5%［8］，对低阻体和高阻体探测均具有极佳的表现，在浅海区资源勘探领域具有良好的应用前景［910］。

目前常用的电磁数值模拟方法包括积分方程法［11］、有限差分法［1214］、有限体积法［15］和有限元法［1619］等。其中有限元法因空间离散灵活，在处理复杂模型时更具自由性和准确性。随着非结构化网格剖分技术的进步，非结构化网格对复杂地形的精细刻画使得基于非结构化网格的有限元法非常适合对复杂地质模型的三维正演［20］。Zhang等［21］直接在时域求解，实现了基于自适应有限元法的航空瞬变电磁三维正演模拟，并分析了地形对航空瞬变电磁响应的影响。齐彦福等［22］和王新宇等［23］基于非结构时域有限元分别开展了电性源短偏移距和长偏移距瞬变电磁在起伏地形影响下的响应特征分析，结果均表明復杂地形与地下目标体相互耦合使得观测响应十分复杂，难以进行有效分辨。周钟航等［24］基于三维非结构时域有限元算法，研究了山峰对电性源地面瞬变电磁响应的影响，并根据叠加原理提出一种以瞬变响应为校正参量的地形效应校正方法。

在海洋电磁法数值模拟方面，高研等［25］采用六面体网格构建了海底可燃冰与油气双储层模型，基于频域矢量有限元研究了不同收发据下可控源音频大地电磁法的响应特征。殷长春等［26］基于非结构有限元，针对海洋电磁半拖拽式和双船拖拽式工作方式，研究了海底起伏地形对时域海洋可控源电磁法的影响及高阻层的响应特征。叶益信等［27］实现了基于非结构化网格的海洋可控源电磁场三维正演，并提出了一种非结构化网格的局部加密方法，有效提高了有限元数值解的精度。Um等［28］基于时域有限元首次使用后推欧拉方法实现了带地形的时域海洋瞬变电磁响应计算。由于使用四面体网格，该方法相比于时域有限差分方法可以更好地拟合复杂海底地形。赵越等［29］研究了不同发射波形下磁性源浅海瞬变电磁的响应特征，并证明了磁性源瞬变电磁适合探测低阻异常体。刘晓等［30］使用时域伪谱法模拟瞬变水平电偶极源对三维海底模型的响应，通过研究早期电磁场幅值随收发据的变化来确定高阻体的存在；但仅研究了磁场强度竖直分量Hz的观测响应，并没有研究电场强度水平分量Ex的响应。通过以上分析可知，当前研究虽开展了部分三维数值模拟工作，但模型设置相对简单，且对复杂地质环境下的响应特征缺乏系统深入的认识，距离实际勘探的要求仍有不小差距。

浅海域多为大陆架区域，作为大陆和海洋的过渡地带，其复杂的地质条件对电磁法畸变效应的影响也更为严重，严重限制了拖拽式电性源瞬变电磁法在复杂条件下的应用效果，使瞬变电磁数据的解释变得十分困难。鉴于电性源瞬变电磁法在浅海地区复杂地质条件下的电磁场响应特征研究较少，本文基于非结构时域有限元法，利用非结构四面体网格对复杂地形模拟的灵活性和准确性，对复杂地质条件下浅海区进行电性源瞬变电磁三维正演模拟。在验证算法的准确性后，讨论不同海水深度下的空气波特征及海底水平油气藏的响应特征，研究浅海地区不同地层电阻率以及海底复杂地形对海底高阻油气资源探测效果的影响，系统开展电性源瞬变电磁三维响应特征分析。

1  时域有限元电磁法控制方程

瞬变电磁法中电场和磁场分量随时间的变化符合时域麦克斯韦方程组：

SymbolQC@×E（r，t）=－B（r，t）t；SymbolQC@×H（r，t）=J（r，t）+Js（r，t）。（1）

式中：r为位置矢量；E（r， t）、B（r， t）、H（r， t）和J（r， t）分别为r处、t时刻的电场强度、磁感应强度、磁场强度和传导电流密度；Js（r， t）为r处、t时刻的外加源电流密度。电流密度和磁场的本构方程为：

J=σ^E；B=μH。（2）

式中：σ^为各向异性电导率张量；μ=μ0μr，为磁导率（μr为相对磁导率；μ0=4π×10-7 H/m）。式（2）第一行为微分形式欧姆定律，第二行为B和H的基本关系。联立式（1）与式（2）即可消去磁场，得到时域电场扩散方程：

SymbolQC@×［1μSymbolQC@×E（r，t）］+σ^E（r，t）t+Js（r，t）t=0。（3）

为了将式（3）转化为时域有限元近似方程，定义残差矢量R（r， t）公式为

R（r，t）=

SymbolQC@×［1μSymbolQC@×E（r，t）］+σ^E（r，t）t+Js（r，t）t。（4）

将计算区域离散成若干个四面体有限单元，并对其进行加权积分，使每个单元的残差矢量被强制为0。假设计算区域Ω内的残差加权体积分为

ΩW（r）·R（r，t）dV=0。（5）

式中：W（r）为加权系数；V为体积。式（5）的意义为使W（r）和R（r， t）的内积最小化，即使W（r）和R（r，t）正交来寻找最优解。将式（4）代入式（5）可得

ΩW（r）·SymbolQC@×［1μSymbolQC@×E（r，t）］dV+ΩW（r）·σ^E（r，t）tdV+ΩW（r）·Js（r，t）tdV=0。（6）

基于第一矢量格林定理，将式（6）第一项的积分展开，得到

ΩW（r）·SymbolQC@×［1μSymbolQC@×E（r，t）］dV=1μ·Ω［SymbolQC@×W（r）］·［SymbolQC@×E（r，t）］dV－1μΓW（r）×［SymbolQC@×E（r，t）］·ndS。（7）

式中：Γ为外边界；n为面的法向量；S为面积。

本文采用非结构四面体网格对计算区域进行离散，采用自动满足电场切向分量连续且无散的矢量插值基函数来近似单元内线性分布的电场。每个四面体单元内任意位置的电场可表示为

E（r，t）=∑6j=1Ej（t）Nj（r）。（8）

式中：Ej（t）为四面体单元第j条棱边的切向电场，可称为自由度；Nj（r）为四面体单元第j条棱边的矢量插值基函数。在伽留金法中采用矢量插值基函数作为加权系数时，内边界面两侧的面积分相互抵消，外边界距离发射源足够远，满足Sommerfeld边界条件。在忽略面积分后，式（7）可写成

ΩW（r）·SymbolQC@×［1μSymbolQC@×E（r，t）］dV=1μΩ［SymbolQC@×W（r）］·［SymbolQC@×E（r，t）］dV。（9）

将式（8）和式（9）代入式（6）可得

1μ∑6j=1Ej（t）Ω［SymbolQC@×N（r）］·［SymbolQC@×N（r）］dV+∑6j=1Ej（t）tΩN（r）·σ^·N（r）dV+ΩN（r）·Js（r，t）tdV=0。  （10）

式中，N（r）为矢量插值基函数。将所有单元加权残差累加，可写成矩阵形式：

SE（t）+MdE（t）dt=－J。（11）

式中：S和M分别为整体刚度矩阵和质量矩阵；E（t）为棱边上的待求电场；J为外加源项。S、M和J具体表达式如下：

S=1μΩ［SymbolQC@×N（r）］·［SymbolQC@×N（r）］dV；M=ΩN（r）·σ^·N（r）dV；J=ΩN（r）·Js（r，t）tdV。（12）

联立式（11）和式（12），采用二阶后推欧拉法近似式中i+2时刻电流密度与电场对时间的导数：

dJ（i+2）s（t）dt=  12Δt［3J（i+2）s（t）－4J（i+1）s（t）+J（i）s（t）］；dE（i+2）（t）dt=  12Δt［3E（i+2）（t）－4E（i+1）（t）+E（i）（t）］。（13）

式中，Δt为时间步长。将式（13）代入到式（11）中可得：

2ΔtJ（i+2）（t）=3J（i+2）（t）－4J（i+1）（t）+J（i）（t）；（3M+2ΔtS）E（i+2）（t）=M［4E（i+1）（t）－  E（i）（t）］－2ΔtJ（i+2）（t）。（14）

由式（14）中的第一行即可得到任意发射电流波形的电流源项，而式（14）中的第二行可简写为

KE=b。（15）

式中：K为系数矩阵；E为棱边上的未知电场；b为已知发射源项。

本文电性源瞬变电磁三维数值模拟采用下阶跃激励方式。下阶跃激励的初始电场E（r，0）由长导线源内部导线的电场E1（r）与导线两端正负电极向地下供电形成的稳定直流电场E2（r）两部分组成：

E（r，0）=E1（r）+E2（r）。（16）

在计算中，往往忽略E1（r），而E2（r）为电位梯度，可通过电势φ（r）的负梯度计算：

E2（r）=－SymbolQC@φ（r）。（17）

設点源位于rs=（xs，ys，zs）处，电流强度为I，基于式（2）中微分形式的欧姆定律及电场连续性易得

SymbolQC@·J（r）=Ιδ（r－rs）。（18）

式中：J（r）为r处的电流密度；δ为脉冲函数。联立式（18）与微分形式的欧姆定律（式（2）第一行），可得到正负点源电场满足的泊松方程：

SymbolQC@·［σ^SymbolQC@φ（r）］=－Iδ（r－rs）。（19）

最后，为保证直流电场与矢量电场边界的一致性，对直流电场与时域电场采用相同的四面体网格，且均采用总场方法求解直流问题与时域电磁问题。实际上，截断边界离发射源很远，因此可以在计算过程中对外边界Γ均施加狄利特雷边界条件：

φ|Γ=0；（n×E）|Γ=0。（20）

2  数值实验

2.1  精度验证

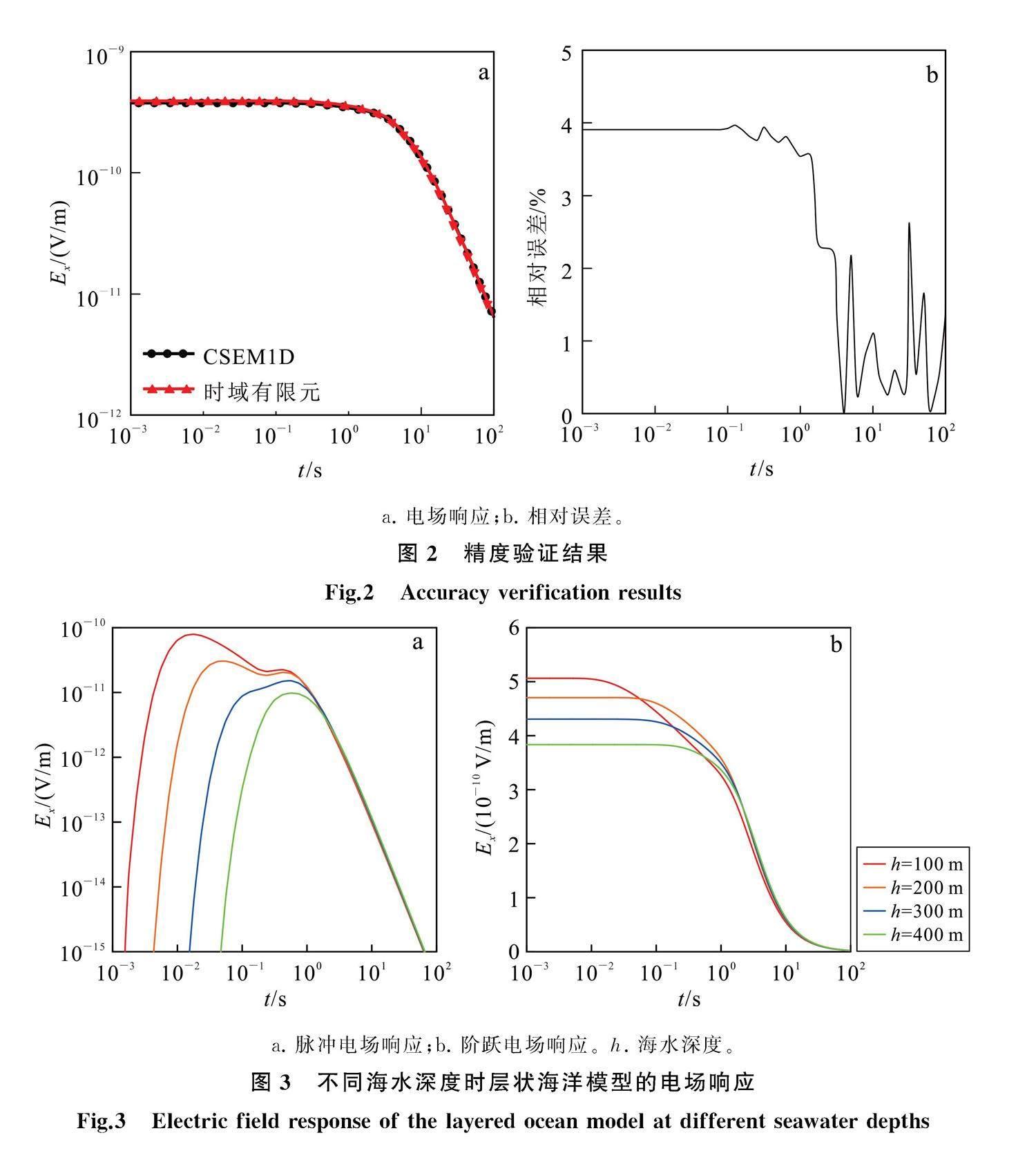
为了验证本文算法的计算精度，设置如图1所示的一维层状海洋模型：海水层厚度为400 m，电阻率为0.3 Ω瘙簚m；上方为空气层，电阻率为108 Ω瘙簚m；下方为海底沉积层，电阻率为1 Ω瘙簚m。工作装置为轴向装置。发射源长度为300 m，中心坐标为（-5 850， 0， 40），距海底40 m，发射电流为1 A，发射源为下阶跃。接收点坐标为（0， 0， 30），距海底30 m。对开源软件CSEM1D［31］和本文算法计算的Ex数据进行了对比，结果如图2所示：本文的计算结果与CSEM1D结果吻合性较好（图2a），相对误差在早期小于4%，晚期小于2%（图2b），有效地验证了本文算法的准确性。

2.2  不同海水深度对分辨率的影响

2.2.1  对空气波的响应

在浅海区内，海洋电磁信号受空气波影响显著。为研究不同海水深度下的空气波特征，参照图1建

立的一维层状海洋模型，将海水深度分别设置为100、200、300和400 m，发射源和接收点位置保持不变，研究了脉冲发射源和阶跃发射源下的电场响应特征，结果如图3所示。由图3a可知：当海水深度小于200 m时，脉冲响应曲线存在两个明显峰值，分别对应空气波响应和海底地层响应；随着海水深度的增加，两个峰值的时间间距逐渐减小，在水深超过300 m时已不能明显区分两个峰值，空气波影响可忽略。由图3b可知，阶跃响应受空气波影响较小，相比于脉冲响应，阶跃响应并不存在明显区分空气波和海底地层响应的两个峰值。

2.2.2  对目标体分辨率的影响

为研究不同海水深度对勘探目标体分辨率的影响，设置了如图4所示的三维地电模型：海水层厚度分别为100、200和400 m，电阻率为0.3 Ω瘙簚m；上方为空气层，电阻率为108 Ω瘙簚m；下方为海底沉积层，电阻率为1 Ω瘙簚m；油气藏大小为4 000 m×4 000 m×200 m，顶部埋深距海底600 m，中心坐标为  （0， 0， -700），电阻率为100 Ω瘙簚m；其余参数同图1一致。

不同海水深度水平海底油气藏模型电场响应计算结果如图5所示。通过分析图5a—f可知，Ex既

随收发距的增大而衰减，也受目标层的影响，在此二因素的叠加下，很难从Ex响应曲线对应位置看出油气藏的影响，需要对总场进行归一化处理。本文通过计算异常场与背景场之比将电场响应转换为相对异常。通过分析图5g、h、i可知，Ex相对异常在靠近发射源一侧出现极小值，在远离发射源一侧出现极大值，两极值点在x轴上位置分别与油气藏的边界位置相对应。Ex相对异常曲线在异常体范围内平缓变化，可从曲线的形态特征分析出异常体的位置

和边界，进而达到对异常体有效识别的目的。当海水深度为100、200和400 m时，最大相对异常

分别

a、b、c. 海水深度分别为100、200、400 m，含有油气藏时的Ex；d、e、f. 海水深度分别为100、200、400 m，不含油气藏时的Ex；g、h、i. 海水深度分别为100、200、400 m时含有油气藏与不含油气藏的Ex相对异常。

为150%、140%和130%，随着海水深度的增加，相对异常峰值出现明显下降，但在水深400 m时仍能对油气藏进行有效识别。

2.3  地层电阻率变化对目标体探测效果的影响

目标体的探测效果受围岩电阻率影响明显。为研究地层电阻率变化对电磁场响应的影响规律，设计了三种海底分层地电模型（图6），三种模型中海水层厚度均为400 m，电阻率为0.3 Ω瘙簚m；海底沉积层共分为两层，地层分界面距海底300 m，异常体大小为4 000 m×4 000 m×2 00 m，顶部埋深距海底600 m，中心坐标为（0， 0， -700），位于下沉积层，高阻时电阻率为100 Ω瘙簚m，低阻时电阻率为0.1 Ω瘙簚m。下沉积层电阻率变化的高阻异常体模型（图6a）中海底上沉积层电阻率为1 Ω瘙簚m，下沉积层电阻率变化，分别为2、5和10 Ω瘙簚m，异常体电

阻率为高阻；上沉积层电阻率变化的高阻异常体模型（图6b）将下沉积层电阻率设置为1 Ω瘙簚m，上沉积层电阻率变化，分别为2、5和10 Ω瘙簚m，异常体电阻率为高阻；下沉积层变化的低阻异常体模型（图6c）将上沉积层电阻率设置为1 Ω瘙簚m，下沉积层电阻率变化，分别为2、5和10 Ω瘙簚m，异常体电阻率为低阻。

图7给出了下沉积层电阻率变化的高阻异常体

模型（图6a）的电场响应，分析可知，当海底地层出现分层情况时，高阻异常体的Ex相对异常曲线特征与异常体的位置和边界仍存在对应关系，且与前文一致。当下沉积层电阻率为2、5和10 Ω瘙簚m时，最大相对异常分别为118%、108%和103％，相对异常峰值随高阻异常所在地层电阻率的增加出現明显降低，曲线形态也由光滑变为崎岖。当下沉积层电阻率为10 Ω瘙簚m时，相对异常曲线形态已经十分复杂，仅通过分析相对异常很难判断异常体的存在和位置。

图8给出了上沉积层电阻率变化的高阻异常体模型（图6b）的电场响应，可以看出，当高阻异常体所在地层电阻率为1 Ω瘙簚m的低阻沉积层时，上沉积层电阻率的增加基本不影响Ex响应曲线的趋势，Ex相对异常曲线也较为光滑，通过观察相对异常峰值位置可以清晰地判断高阻异常体的位置和边界。当上沉积层电阻率为2、5和10 Ω瘙簚m时，最大相对异常分别为130%、125%和118％：与水平海底油气藏模型（图5）相比，上沉积层电阻率的增加虽导致相对异常峰值有所下降，但仍可以达到对异常体有效识别的目的；相比于下沉积层电阻率变化的高阻异常体模型（图7）而言，影响较小。

图9给出了下沉积层变化的低阻异常体模型（图6c）的电场响应。可以看到，当低阻异常所在地层电阻率增大时，Ex响应曲线的变化趋势同目标体为高阻、下沉积层电阻率变化时的Ex响应曲线（图7）相比，在低阻异常位置内曲线的形态出现明显弯曲（图9a、b、c）。在图9d、e、f中，下沉积层电阻率分别为2、5和10 Ω瘙簚m时，最大相对异常分别为120%、115%和111％，相对异常峰值同样随异常体所在地层电阻率的增加而降低。不同的是，与高阻异常相比，低阻异常的相对异常曲线形态发生改变，曲线特征表现为在靠近和远离发射源处出现两个峰值，分别对应低阻异常体两侧边界位置；在两峰值中间出现一极小值，对应异常体中心位置。与高阻异常相对异常曲线相比，低阻异常的相对异常曲线峰值位置与异常体边界位置出现偏差，并不能很好地判断低阻异常体的位置和边界。

为了进一步分析海底地层电阻率变化对电磁场响应特征的影响以及高/低阻异常出现不同响应特征曲线的原因，绘制了如图10所示的t=1 s时的地下电场分布及电场矢量图。图10a、b对应下沉积

层电阻率变化（2、10 Ω瘙簚m）的高阻异常体模型；图10c、d对应下沉积层变化（2、10 Ω瘙簚m）的低阻异常体模型。由图10易得，无论是高阻还是低阻异常体，红色虚线方框附近的电场响应及电流密度矢量图均发生了严重的畸变。在图10a、b中，感应电流表现为垂直穿过高阻异常体，并围绕高阻异常体周围产生电流通道效应；在图10c、d中，低阻异常对电流存在吸引作用，感应电流沿x方向在低阻异常体内平行通过，并产生明显的电流通道效应，异常体两端边界处的电流流向均发生明显改变，且变化幅度随地层电阻率的增加而变大。与高阻异常体不同的是，低阻异常体两端边界处的电流方向变化明显。矢量

图很好地解释了高阻异常和低阻异常出现不同响应特征曲线的原因。

2.4  海底起伏地形对目标体探测效果的影响

我们设计了山峰地形模型和山谷地形模型，以研究电性源瞬变电磁场在海底复杂地形条件下的响应特征。

2.4.1  山峰地形

在山峰地形高阻油气藏模型（图11）中，通过改变山峰高度更好地分析山峰地形带来的影响。峰顶距海底平面分别为200和250 m，x和y方向长均为2 000 m，在山峰下方含有高阻油气藏，接收点测线沿海底地形布置，始终保持距离海底表面30 m，其余参数与图1保持一致。

图12为山峰地形高阻油气藏模型电场响应。从图12a、b可以看到，由于测点沿地形布置，因此山峰地形高阻油气藏模型Ex响应曲线的形态随地形发生改变，且曲线形态与地形一致，受地形影响，油气藏响应被地形响应所淹没。图12c、d为山峰地形下含有油气藏与水平地形下含有油气藏的Ex相对异常曲线，可以清晰地看到地形起伏情况。图12e、f为山峰地形下含有油气藏与不含油气藏的Ex相对异常曲线，与水平海底油气藏模型相似，相对异常曲

线形态与异常体位置和边界仍存在对应关系；当山峰高度为200 m时，相对异常的极值点与高阻异常的边界位置吻合良好，最大相对异常为125%（图12e），相较于水平海底地形出现小幅度降低，但仍具有较高分辨率；当山峰高度为250 m时，尽管相对异常峰值没有下降，但曲线形态发生了明显的改变，远离发射源一侧的相对异常极值点位置发生偏离（图12f），无法准确判断异常体边界所在，说明地形因素对电性源瞬变电磁在浅海区的探测效果有一定的影响。图12g、h为山峰地形下含有油气藏与海底水平地形下不含油气藏的Ex相对异常曲线，可以看出受山峰地形的影响，靠近发射源一侧的相对异

常极小值不再明显，曲线在山峰边界处及峰顶位置均出现明显波峰，曲线形态与山峰地形形态一致，并随着山峰高度的增加变得更为明显，在远离发射源一侧相对异常极大值仍对应异常体边界位置。

2.4.2  山谷地形

在山谷地形高阻油气藏模型（图13）中，谷底距海底平面200 m，x和y方向长2 000 m，在谷底下方埋有高阻油气藏，接收点测线沿地形布置，始终保持距离海底表面30 m，其余參数与图1保持一致。

图14为山谷地形高阻油气藏模型电场响应。从图14a可以看出，山谷地形下含有油气藏时Ex响应曲线同山峰地形一致，曲线形态同样随地形发生改变，且曲线形态与地形一致。图14b为山谷地形下含有油气藏与水平海底下含有油气藏的Ex相对异常曲线，从中可以清晰看到地形起伏情况。图14c为山谷地形下含有油气藏与不含油气藏的Ex相对异常曲线，曲线出现两个极值点，对应异常体的边界位置，最大相对异常为126%，相较于水平海底地形出现小幅度降低，但仍具有较高分辨率，可以对异常体进行有效识别和探测。图14d为山谷地形下含有油气藏与海底水平地形下不含油气藏的Ex相对异常曲线，可以看出受山谷地形影响，靠近发射源一侧的相对异常极小值不再明显，曲线在山谷边界处出现明显波峰，在谷底位置出现波谷，在远离发射源一侧相对异常极大值仍对应异常体边界位置。

因此，在浅海地区进行电性源瞬变电磁探测时，可以依靠声纳系统测定海底地形，并计算海底半空

间响应，通过计算海底异常体的相对异常，实现对海

底起伏地形下异常体的有效探测。

为了进一步研究地形对瞬变电磁法响应特征的影响，绘制了海底山峰地形和海底山谷地形高阻油气藏模型的电场分布及电场矢量图（图15）。从图15中可以看出，地形的起伏会影响电场响应及电场矢量，电流方向在海底山峰、山谷地形处发生改变。结合上文对海底地层电阻率变化时电场响应的研究，山峰/山谷地形可以分别看作是一局部高/低阻

a. 山谷地形下含有油气藏的Ex；b. 山谷地形下含有油气藏与海底水平地形下含有油气藏的Ex相对异常；c. 山谷地形下含有油气藏与山谷地形下不含油气藏的Ex相对异常；d. 山谷地形下含有油气藏与海底水平地形下不含油气藏的Ex相对异常。

a. 山峰地形高阻油气藏模型；b. 山谷地形高阻油气藏模型。红色实线表示海底沉积层分界线；红色虚框表示异常体。

体，因此相比于海底山峰地形，海底山谷地形条件下浅海电性源瞬变电磁对异常体的识别能力有所提高。

3  结论

本文基于时域有限元法，利用非结构四面体网格的灵活性对复杂地质模型进行构建，实现了电性源瞬变电磁在浅海区复杂地质条件下的三维响应特征分析。通过大量数值模拟得出以下结论：

1）脉冲响应受空气波影响较大，海水深度超300 m时可忽略空气波影响，阶跃响应受空气波影响明显减小；电性源瞬变电磁脉冲响应和阶跃响应在浅海区均可有效分辨海底地层响应，在海水深度100～400 m范围内可对高阻异常体进行有效识别。

2）相對异常曲线的峰值大小可反映出探测效果的好坏，同时利用相对异常曲线峰值位置可以很好地界定高阻异常体的位置和边界，但对低阻异常而言，识别效果有所下降。

3）在海底地层分层情况下，地层电阻率的变化对电性源瞬变电磁探测效果影响较大，特别是异常体所在沉积层电阻率增加时，相对异常峰值出现明显下降，沉积层电阻率为10 Ω·m时异常体的响应特征已十分微弱，无法达到有效识别的目的。

4）浅海区海底地形会对电性源瞬变电磁的探测效果造成一定影响，可以通过测定海底地形半空间响应并计算相对异常，来界定异常体的位置和边界。相比于山谷地形，山峰地形对探测效果影响更为严重，并随着山峰地形高度的增加，相对异常峰值点出现偏移，探测精度有所下降。在实际勘探中，必须考虑地形因素带来的影响。

参考文献（References）：

［1］  何展翔，余刚.海洋电磁勘探技术及新进展［J］.勘探地球物理进展，2008，31（1）： 29.

He Zhanxiang， Yu Gang. Marine EM Survey Technology and Its New Advances［J］. Progress in Exploration Geophysics， 2008， 31（1）： 29.

［2］  付元宾，王伟伟，张建民.海洋管理中的海洋区域划分方案探讨［J］.海洋开发与管理，2013，30（8）： 2023.

Fu Yuanbin， Wang Weiwei， Zhang Jianmin. Discussion on Marine Zoning Programmes in Ocean Management［J］. Ocean Development and Management， 2013， 30（8）： 2023.

［3］  李建忠.第四次油气资源评价［M］.北京：石油工业出版社，2019.

Li Jianzhong. Fourth Oil and Gas Resources Assessment［M］. Beijing： Petroleum Industry Press， 2019.

［4］  李予国，Steven Constable.浅水区的瞬变电磁法：一维数值模拟结果分析 ［J］.地球物理学报，2010，53（3）：737742.

Li Yuguo，Constable S. Transient Electromagnetic in Shallow Water： Insights from 1D Modeling［J］. Chinese Journal of Geophysics， 2010， 53（3）： 737742.

［5］  刘婷婷，李予国.海洋可控源电磁法对天然气水合物高阻薄层的可探测度［J］.海洋地质前沿，2015，31（6）：1722.

Liu Tingting， Li Yuguo. Detectability of High-Resistance Thin Layer of Gas Hydrate by Marine Controllable Source Electromagnetic Method［J］. Marine Geology Frontiers， 2015， 31（6）： 1722.

［6］  薛国强，李貅，底青云.瞬变电磁法理论与应用研究进展［J］.地球物理学进展，2007，22（4）：11951200.

Xue Guoqiang， Li Xiu， Di Qingyun. The Progress of TEM in Theory and Application［J］. Progress in Geophysics， 2007， 22（4）： 11951200.

［7］  赵越，孙怀凤，刘佳，等.浅海磁性源瞬变电磁探测技术及其应用研究［J］.地球物理学进展，2023，38（6）：27682777.

Zhao Yue， Sun Huaifeng， Liu Jia， et al. Technology of Shallow Sea Magnetic Sources TEM Detection and Its Application［J］. Progress in Geophysics， 2023， 38（6）： 27682777.

［8］  Eid Rami. Numerical Modelling of Geophysical Monitoring Techniques for CCS［D］. Edinburgh： The University of Edinburgh， 2016.

［9］  王显祥，底青云，唐静.电性源瞬变电磁初探［J］.地球物理学进展，2015，30（2）：872877.

Wang Xianxiang， Di Qingyun， Tang Jing. The Preliminary Study of the Ground Source Transient［J］. Progress in Geophysics， 2015， 30（2）： 872877.

［10］  王新宇，严良俊，毛玉蓉.电性源瞬变电磁法油气藏动态监测模拟分析［J］.石油地球物理勘探，2022，57（2）：459466.

Wang Xinyu， Yan Liangjun， Mao Yurong. Simulation and Analysis of Dynamic Monitoring of Oil and Gas Reservoir Based on Grounded Electric Source TEM［J］. Petroleum Geophysical Exploration， 2022， 57（2）： 459466.

［11］  Zhdanov M S. Integral Equation Method for 3D Modeling of Electromagnetic Fields in Complex Structures with Inhomogeneous Background Conductivity in Marine CSEM Applications［J］. Seg Technical Program Expanded Abstracts， 2005， 71（6）： G333G345.

［12］  Commer M， Newman G. A Parallel Finite-Difference Approach for 3D Transient Electromagnetic Modeling with Galvanic Sources［J］. Geophysics， 2004， 69（10）： 11921202.

［13］  董浩，魏文博，葉高峰，等.基于有限差分正演的带地形三维大地电磁反演方法［J］.地球物理学报，2014，57（3）：939952.

Dong Hao， Wei Wenbo， Ye Gaofeng， et al. Study of Three-Dimensional Magnetotelluric Inversion Including Surface Topography Based on Finite-Difference Method［J］. Chinese Journal of Geophysics， 2014， 57（3）： 939952.

［14］  Li J， Hu X， Cai H， et al. A Finite-Element Time-Domain Forward-Modelling Algorithm for Transient Electromagnetics Excited by Grounded-Wire Sources［J］. Geophysical Prospecting， 2020， 68（4）： 13791398.

［15］  Liu W， Farquharson C G， Zhou J， et al. A Rational Krylov Subspace Method for 3D Modeling of Grounded Electrical Source Airborne Time-Domain Electromagnetic Data［J］. Journal of Geophysics and Engineering， 2019， 16（2）： 451462.

［16］  Mitsuhata Y. 2D Electromagnetic Modeling by Finite-Element Method with a Dipole Source and Topography［J］. Geophysics， 2000， 65（2）： 465475.

［17］  Lin C， Tan H， Wang W， et al. Three-Dimensional Inversion of CSAMT Data in the Presence of Topography［J］. Exploration Geophysics， 2017， 49（3）： 253267.

［18］  Brner R U， Ernst O G， Spitzer K. Fast 3D Simulation of Transient Electromagnetic Fields by Model Reduction in the Frequency Domain Using Krylov Subspace Projection［J］. Geophysical Journal of the Royal Astronomical Society， 2010， 173（3）： 766780.

［19］  张鑫崇，殷长春. 基于Debye模型的时间域航空电磁激电效应正演模拟［J］. 吉林大学学报（地球科学版），2023，53（5）：15731581.

Zhang Xinchong， Yin Changchun. Forward Modeling of Airborne Electromagnetic  Induced Polarization Effect in Time-Domain Based on Debye Model［J］. Journal of Jilin University （Earth Science Edition）， 2023， 53 （5）： 15731581.

［20］  任政勇，汤井田.基于局部加密非结构化网格的三维电阻率法有限元数值模拟［J］.地球物理学报，2009，52（10）：26272634.

Ren Zhengyong， Tang Jingtian. Finite Element Modeling of 3D DC Resistivity Using Locally Refined Unstructured Meshes［J］. Chinese Journal of Geophysics， 2009， 52（10）： 26272634.

［21］  Zhang B， Yin C， Ren X， et al. Adaptive Finite Element for 3D Time-Domain Airborne Electromagnetic Modeling Based on Hybrid Posterior Error Estimation［J］. Geophysics： Journal of the Society of Exploration Geophysicists， 2018， 83（2）： WB71WB79.

［22］  齐彦福，李貅，孙乃泉，等.电性源短偏移距瞬变电磁地形影响特征分析［J］.吉林大学学报（地球科学版），2022，52（1）：247260.

Qi Yanfu， Li Xiu， Sun Naiquan， et al. Analysis of Influcence Characteristics of Topography on Grounded-Source Short-Offset Transient Electromagnetic Responses［J］. Journal of Jilin University （Earth Science Edition）， 2022， 52（1）： 247260.

［23］  王新宇，严良俊，毛玉蓉，等.起伏地形条件下长偏移距瞬变电磁三维正演［J］.吉林大学学报（地球科学版），2022，52（3）：754765.

Wang Xinyu， Yan Liangjun， Mao Yurong， et al. Three-Dimensional Forward Modeling of Long-Offset Transient Electromagnetic Method over Topography［J］. Journal of Jilin University （Earth Science Edition）， 2022， 52（3）： 754765.

［24］  周钟航，张莹莹.山峰对电性源地面瞬变电磁响应的影响及校正方法［J］.物探与化探，2023，47（5）：12361249.

Zhou Zhonghang， Zhang Yingying. Crection of the Intutence of Mountains on Grounded-Source Transient Electromagnetic Responses ［J］. Geophysical & Geochemical Exploration， 2023， 47（5）： 12361249.

［25］  高妍，馬超，张向宇.可燃冰与油气双储层模型的海洋可控源电磁响应特征模拟分析［J］.石油地球物理勘探，2022， 57（4）：950962.

Gao Yan，Ma Chao，Zhang Xiangyu. Characteristics of Simulated Marine Controlled-Source Electromagnetic Responses of Coupled Gas Hydrate and Petroleum Reservoir Models［J］. Oil Geophysical Prospecting， 2022， 57（4）： 950962.

［26］  殷长春，惠哲剑，张博，等.起伏海底地形时间域海洋电磁三维自适应正演模拟［J］.地球物理学报，2019，62（5）：19421953.

Yin Changchun， Hui Zhejian， Zhang Bo， et al. 3D Adaptive Forward Modeling for Time-Domain Marine CSEM over Topographic Seafloor［J］. Chinese Journal of Geophysics， 2019，62（5）： 19421953.

［27］  叶益信，李予国，刘颖，等.基于局部加密非结构网格的海洋可控源电磁法三维有限元正演［J］.地球物理学报，2016， 59（12）：47474758.

Ye Yixin， Li Yuguo， Liu Ying， et al. 3D Finite Element Modeling of Marine Controlled-Source Electromagnetic Fields Using Locally Refined Unstructured Meshes［J］. Chinese Journal of Geophysics， 2016， 59（12）： 47474758.

［28］  Um E S， Harris J M， Alumbaugh D L. 3D Time-Domain Simulation of Electromagnetic Diffusion Phenomena： A Finite Element Electric-Field Approach［J］. Geophysics， 2010， 75（4）： F115F126.

［29］  赵越，许枫，李貅，等.浅海瞬变电磁全波形响应特征及探测能力分析［J］.地球物理学报，2019，62（4）：15261540.

Zhao Yue， Xu Feng， Li Xiu， et al. Exploration Capability of Transmitter Current Waveform on Shallow Water TEM Response［J］. Chinese Journal of Geophysics， 2019，62（4）： 15261540.

［30］  刘晓， 谭捍东，汪茂，等.电偶源海洋瞬变电磁法三维数值模拟与响应特征研究［J］.科学技术与工程，2016，16（4）： 16.

Liu Xiao， Tan Handong， Wang Mao， et al. A Study of 3D Marine TEM Modeling and Response Characterization of Electric Dipole Source［J］. Science Technology and Engineering， 2016， 16（4）： 16.

［31］  Key K. Is the Fast Hankel Transform Faster than Quadrature？［J］. Geophysics： Journal of the Society of Exploration Geophysicists， 2012， 77（3）： F21F30.