UWB 通信中高斯脉冲的应用及关键技术综述

雍长娟 石雁祥

摘要：超宽带（Ultra Wide Band，簡称UWB） 通信系统发射的信号具有极窄的脉冲宽度和极其广阔的频谱特性。为防止对现有通信系统的潜在干扰，并最大化利用频谱资源，有必要研究设计出满足美国联邦通信委员会（FCC） 所制定的超宽带信号辐射掩模标准的功率谱密度。为了探寻既能满足辐射掩模标准又能充分利用频谱资源的最佳超宽带脉冲信号形式，研究人员对各种不同形态的高斯脉冲进行了广泛而深入的研究。本文系统回顾了近20年来在UWB通信系统中，关于高斯脉冲信号的波形生成、系统兼容性及抗时间抖动这三个关键技术问题的研究进展。

关键词：UWB；FCC辐射掩模；高斯脉冲；关键技术

中图分类号：TN914.2 文献标识码：A

文章编号：1009-3044（2024）11-0005-04

0 引言

超宽带（Ultra Wide Band，简称UWB） 技术起源于20世纪60年代，其原理首先在1990年由美国军方提出，是一种采用1GHz以上极宽频率带宽的超窄脉冲进行无线通信的技术方案。一套完整的超宽带通信系统主要由发射单元、无线传输通道和接收单元三个核心组成部分构成。

为防止对已存在的通信系统造成不必要的干扰，必须将超宽带系统的发射功率严格限制在特定区间内。美国联邦通信委员会（FCC） 对超宽带通信占用的频带资源设定了明确的规范，旨在确保超宽带通信和其他通信之间和谐共存，彼此间不产生相互干扰。

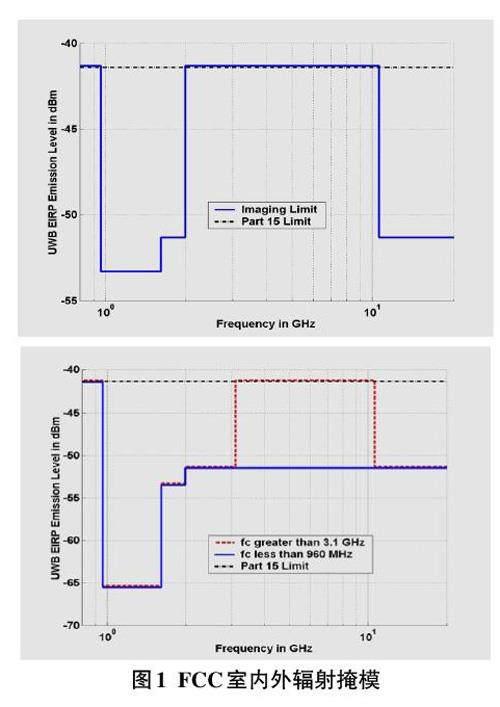
辐射掩模（emission mask） 标准界定了UWB发射信号在不同频段上所允许的最大极限功率谱密度，数值为-41.3 dBm/MHz。这一标准明确规定，UWB发射信号在任何一个频段内的功率谱密度都不能超过该频段所设定的极限值，如图1所示。

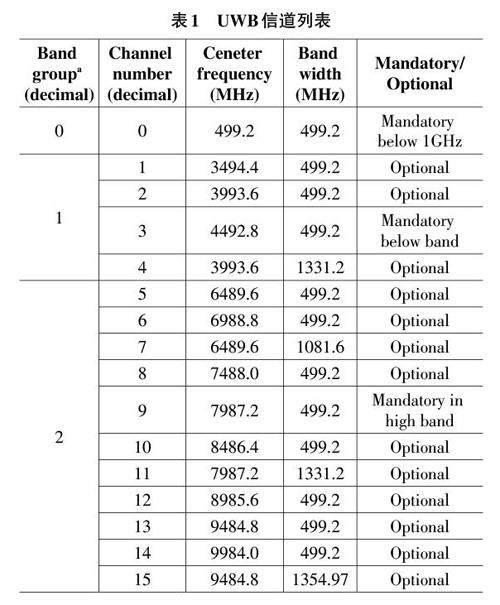
UWB通信系统中，一方面要求发射脉冲的频谱在不超过辐射掩模的前提下尽可能接近辐射掩模，以充分利用该频段内的频谱资源；另一方面，还需考虑脉冲形状对接收机带宽选择及误码率性能的影响。因此，超宽带脉冲的选择显得尤为重要。UWB信道列表如表1所示。在UWB通信领域中广泛应用的主要脉冲类型包括高斯脉冲、Rayleigh脉冲、Laplacian脉冲以及Hermite脉冲。高斯脉冲因其形状可调且在大部分频段能够较好地满足FCC所设定的辐射掩模标准，特别是在高频段能够高效利用频率资源，其生成电路相对简单、成本效益高，对信道衰落现象不敏感，因此在无线通信领域中得到越来越广泛的应用，成为UWB通信中最常见的通信信号之一。

1 高斯脉冲在UWB 通信中的关键技术要点

在UWB通信系统中，发射的高斯脉冲信号的功率直接关乎信号的传输距离，并且必须满足辐射掩模的限制条件。为此，选择合适的方法生成适当的超宽带高斯脉冲至关重要，需解决以下几项关键技术：

1） 脉冲波形生成问题。在确保满足辐射掩模的前提下，如何通过更短的高斯脉冲传递更多信息。

2） UWB通信系统的兼容性问题。系统设计须遵循国际无线电频谱管理规定，确保与现存通信系统之间互不干扰。

3） 抗时间抖动技术问题。UWB通信对系统定时精度要求极高，即便是微乎其微的纳秒级误差也可能导致系统性能急剧下滑，使得接收到的信号与其理想定时位置产生偏差。

1.1 脉冲波形生成问题详解

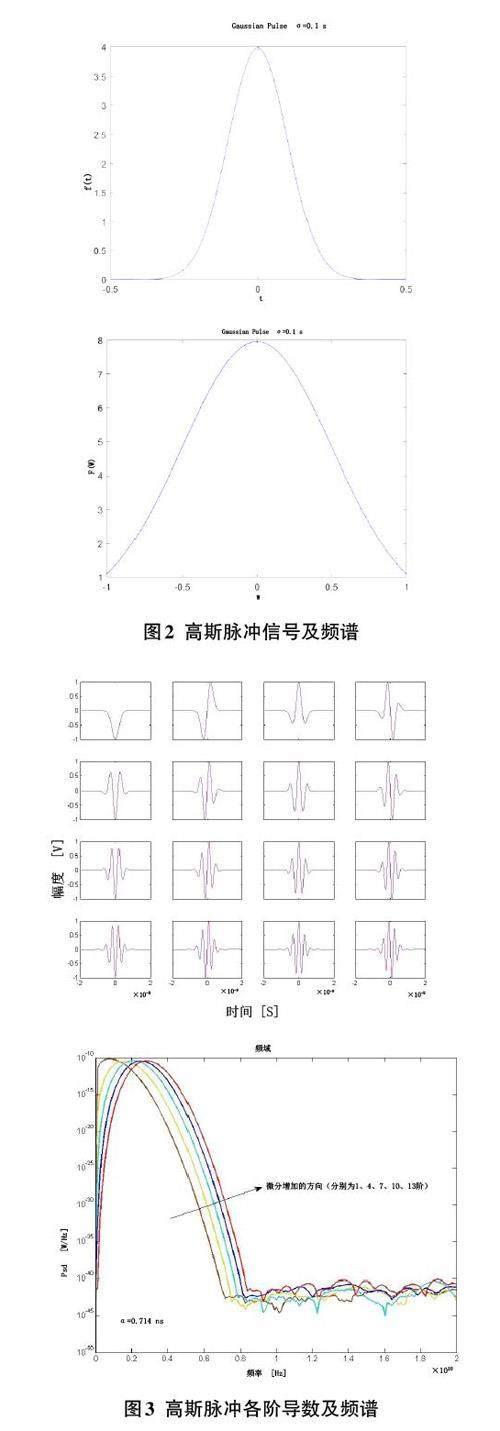
不同类型高斯脉冲的频谱特性差异显著，为设计出合适的高斯脉冲，首要考量的是其频谱必须满足FCC对UWB功率谱密度的限制要求。其次，在此限制条件下，应努力使脉冲频谱尽可能贴近FCC规定的频谱掩模，以便更充分地利用频谱资源。为此，需要对高斯脉冲的成形因子、高斯导函数的阶数以及导函数的不同线性组合方式进行合理选择。图2和图3分别展示了高斯脉冲信号在时域及频域的表现，以及高斯脉冲各阶导数及其对应的频谱图像。

Nardis L D等学者指出，通过减小成形因子α 可以满足超宽带信号对宽阔带宽的需求，而调整高斯脉冲导数的阶数k 则有助于适应超宽带信号对不同峰值频率的诉求[1]。基于此理论基础，岳莉等人进一步探讨了高斯脉冲如何更有效地逼近辐射掩模的两种场景。一种方案是在保持脉冲成形因子α 恒定（设为α=0.714 ns） 的情况下，研究高斯脉冲前15阶导函数在逼近辐射掩模方面的表现[2]。周刘蕾则运用函数逼近的方法，选择了1至8阶的高斯脉冲导函数作为基础函数构建组合，通过为不同阶的高斯脉冲设置各异的成形因子和权重并进行迭代计算，最终确定出最能有效逼近辐射掩模的最优脉冲成形因子和权重值[3]。胡佳伟等人设计了三种类型的组合脉冲结构。第一种构造方法采用了5个具有不同成形因子和权重的二阶高斯脉冲导函数进行线性组合；第二种方案采用5个阶数从1阶至5阶不等的高斯脉冲导函数进行组合，其中每个导函数不仅阶数不同，而且各自具有独立的成形因子和权重；第三种结构是在第二种方案上进一步发展，通过遗传算法对各个基函数的权重进行了优化处理[4]。

白智全提出了一个易于实现、计算复杂度较低的频谱位移高斯波形（SSGW） 算法。该算法通过将高斯脉冲与不同的加权正弦载波相乘，实现了从时域到频域的转换，在极低的实现复杂度下生成满足辐射掩模频谱要求的UWB脉冲[5]。李佩琳等人针对高斯脉冲函数的前10阶归一化导函数提出了两种组合模式：一种是采用成形因子α 均相同的高斯脉冲导函数进行组合；另一种则是采取成形因子α 各异的高斯脉冲导函数进行组合[6]。Ante Milos等人基于埃尔米特多项式，对组合高斯脉冲各阶导数进行了加权处理，进而提出了一种适用于超宽带通信系统的对称高斯脉冲波形[7]。

综上所述，Nardis L D等人的研究成果揭示了在满足FCC辐射掩模规范的前提下，组合脉冲信号在逼近辐射掩模方面表现出优越性，特别是由遗传算法优化得到的权重组合以及基于埃尔米特多项式的两种组合高斯脉冲方案能够在全频段范围内更优地逼近辐射掩模。对于单一高斯脉冲信号而言，随着高斯脉冲导函数阶数k 的增加，其功率谱密度在高频段能更准确地逼近辐射掩模要求；另一种策略是保持高斯脉冲导数阶数k 不变，仅调节成形因子，结果显示，当k固定时，随着成形因子α 增大，高斯脉冲功率谱密度峰值对应的频率将会降低。通过调控成形因子α 和导数阶数k 这两个参数，即可满足UWB系统对传输信号多样频谱特性的需求。图4为Nardis L D等人关于UWB脉冲波形产生问题的实验结果。

1.2 兼容性问题

UWB技術能充分利用有限频率资源，但其通信系统因采用持续时间极短的脉冲作为发射信号，占用频谱资源多，容易对窄带通信系统产生干扰，当高斯脉冲信号功率谱中的离散分量越少，信号功率在整个频带上分布越均匀，越能减小对窄带系统的干扰。UWB 要解决的兼容性问题实际上是解决通信中的相互干扰问题[8-9]。如图5为信号干扰UWB系统接收机的数学模型。

王勇等人为将中心频率搬移到满足辐射掩模的合适位置，他们将绝对带宽较小的高斯脉冲和高频正弦波相乘。脉宽为0.24ns 的正弦调制高斯脉冲的-10dB带宽是03.1～10.6GHz，正好满足FCC的频谱限制[10]。王勇进一步研究了UWB卫星通信系统与窄带系统互相干扰的情况，提出了一种在Ka波段上脉宽为6ns，载频为20GH0z，-20dB带宽为500MHz的THPAM正弦调制高斯脉冲[11]。周刘蕾等人提出了基于软频谱技术认知超宽带系统共存和从接收端出发解决干扰抑制的两种方案[12]。徐晓萍等人分别研究了高斯脉冲波形、调制高斯脉冲信号和调制高斯脉冲序列对UWB 系统兼容性的影响[13]。针对单窄带干扰（NBI） 和双窄带干扰，Elkhamy R S等人考虑了实际的IEEE 802.15.4a UWB 系统与在5.2 GHz 运行的IEEE802.11无线局域网系统以及在8.5 GHz运行的无线电定位系统的共存情况。讨论并比较了由帕克斯-麦克莱伦（PM） 算法和特征值分解（EVD） 法给出的两种脉冲设计方案，对信号功率谱密度（PSD） 和误码率（BER） 的影响[14]。Abhishek Sharma等人提出一种具有控制传输功率谱密度能力的脉冲整形方法。该方法能减少对共用通信波段的干扰[15]。

解决兼容性问题的主要方案为改变脉冲波形和抑制接收端的干扰。当UWB系统中心频率附近出现更高速率的窄带信号或遇到更加苛刻的通信条件，可以采取降低通信速率或采取自适应陷波的方式实现与窄带系统共存，而在改变波形以抗干扰的方案中PM算法给出的脉冲在单窄带干扰的情况下抗干扰能力强，在双NBI的情况下，PM算法和EVD算法给出的两种脉冲抗干扰能力几乎相同。基于最小均方误差（MMSE） 准则和基于谱估计进行干扰对消的UWB接收机方案可以抑制接收端的干扰。

1.3 抗时间抖动问题

时间抖动是收发信机之间的不同步以及收发间的相对速率等因素引起接收信号的时间偏差，时间抖动在非理想信道环境下传输的超宽带通信系统中是不可避免的。一般的超宽带系统均假设发射机和接收机之间准确的传播时延为已知，收发双方完全同步，而任何系统收发双方必然存在着同步误差。UWB脉冲信号持续时间非常短，因此它对时间抖动非常敏感。时间抖动有时会显著降低系统的性能。

文献[16-21]研究了单脉冲UWB系统的时间抖动问题。对于一定的抖动值，所采用的脉冲形状的自相关函数是对系统性能的直接度量。自相关函数的谷值随高斯脉冲导函数阶数增加而降低，函数波形自相关函数的主瓣宽度减小，UWB系统受时间抖动的影响越大，脉冲信号在高频段的频率越高，受时间抖动的影响越严重，误码率也会越大。

M.Z. Win研究了脉冲超宽带环境中采样信号的有效功率谱密度[22]，A. V. Balakrishnan和B. Liu等人研究了时间抖动对通信信号的频率、功率谱密度和抖动的误差界限的影响[23-24]。结果表明，时间抖动的不对称性对功率谱密度没有影响，当生成序列为零均值且不相关时，时间抖动不影响功率谱密度，脉冲形状自相关函数的相关性越大，时间抖动对脉冲信号功率谱的影响越小，误差界限只依赖于抖动的类型和方差，而不依赖于其他抖动统计数据。

2 讨论

在超宽带通信系统中产生的脉冲是其通信技术的关键，其特性与脉冲形状直接相关。高斯脉冲的脉冲形状可调，在绝大部分频段都能很好地满足FCC所规定的辐射掩模。同时，通过对高斯脉冲进行优化，UWB的系统兼容性问题及抗时间抖动问题也能给予较好的解决。高斯脉冲信号在通过电离层与卫星通信时，电离层等离子体会对高斯脉冲信号的辐射掩模、兼容性及抗时间抖动产生一定的影响。需要注意的是，随着人类活动的增加，大量的尘埃粒子进入地球电离层，当电离层某一区域的尘埃粒子浓度达到一定值时，该区域的等离子体变成弱电离尘埃等离子体，弱电离尘埃等离子体对UWB通信中高斯脉冲的影响与一般等离子体会有很大的不同。研究弱电离尘埃等离子体对超宽带通信中高斯脉冲信号的影响是一个值得关注的问题。

参考文献：

[1] DE NARDIS L，GIANCOLA G，DI BENEDETTO M G. Power limits fulfilment and MUI reduction based on pulse shaping in UWB networks[C]//2004 IEEE International Conference on Communications. Paris，France. IEEE，2004：3576-3580.

[2] 岳莉，王毓东，杨旭东. UWB系统中高斯脉冲信号特性的研究[J]. 长春大学学报，2007，17（8）：41-45.

[3] 周刘蕾，朱洪波. 满足FCC辐射掩模的UWB信号设计算法及性能分析[J]. 微波学报，2007，23（4）：32-36.

[4] HU J W，JIANG T，CUI Z G，et al. Design of UWB pulses based on Gaussian pulse[C]//2008 3rd IEEE International Conference on Nano/Micro Engineered and Molecular Systems. Sanya，China. IEEE，2008：651-655.

[5] BAI Z Q，LIU J，CHEN H. Design of ultra‐wideband pulses based on spectrum shifted Gaussian waveforms[J]. IET Communications，7（6）：512-520.

[6] 李佩琳，周青松，张剑云. 基于高斯导函数的超宽带脉冲设计[J]. 通信技术，2018，51（7）：1511-1515.

[7] MILOS A， MOLNAR G， VUCIC M. Spectrally efficient UWB pulse shaping based on polynomially weighted Gaussian pulses with maximally flat amplitude spectra[J]. IEEE Communications Letters，2023，27（7）：1869-1873.

[8] JIANG T，WANG X H，CUI Z G. Analysis on interference of DSUWB signal to narrowband systems[C]//2006 17th International Zurich Symposium on Electromagnetic Compatibility. Singapore. IEEE，2006：269-272.

[9] 崔振刚，郭黎利，姜弢，等. DS-UWB通信系统的信号兼容性分析[J]. 船舶工程，2008，30（1）：41-45.

[10] 王勇，于大鹏.一种用于UWB通信的正弦调制高斯脉冲[J]. 无线电通信技术，2005，31（1）：9-10，53.

[11] 王勇，胡以华.UWB卫星通信系统与窄带系统互扰分析[J]. 电路与系统学报，2013，18（2）：326-330，336.

[12] 周刘蕾.超宽带与窄带通信系统共存的关键技术研究[D]. 南京：南京邮电大学，2008.

[13]徐晓萍， 王春军. 超宽带无线电信号与其他无线通信系统的共存性研究[C]//2009国际信息技术与应用论坛论文集，2009：479-482.

[14] EL-KHAMY R S，SHAABAN S，GHALEB I，et al.Performance of the ieee 802.15.4a uwb system using two pulse shaping techniques in presence of single and double narrowband interferences[J]. International Journal of Wireless & Mobile Networks，2013，5（3）：35-44.

[15] SHARMA A，SHARMA S K.Spectral efficient pulse shape design for UWB communication with reduced ringing effect and performance evaluation for IEEE 802.15.4a channel[J].Wireless Networks，2019，25（5）：2723-2740.

[16] 李耀民，周正.具有同步跟踪功能的单用户TH-SSPPM超宽带系统性能分析[J]. 电子与信息学报，2004，26（12）：1958-1964.

[17] GUVENC I，ARSLAN H.Performance evaluation of UWB systems in the presence of timing jitter[C]//IEEE Conference on Ultra Wideband Systems and Technologies.Reston，VA，USA.IEEE，2003：136-141.

[18] HOR P B，KO C C，ZHI W J.BER performance of pulsed UWB system in the presence of colored timing jitter[C]//2004 International Workshop on Ultra Wideband Systems Joint with Conference on Ultra Wideband Systems and Technologies.Joint UWBST & IWUWBS 2004. Kyoto， Japan. IEEE， 2004：293-297.

[19] LOVELACE W M，TOWNSEND J K.The effects of timing jitter and tracking on the performance of impulse radio[J].IEEE Journal on Selected Areas in Communications， 2002， 20（9）：1646-1651.

[20] FORGAC J，FARKAS P.Analysis of different UWB systems with timing jitter and ISI in AWGN channel[C]//SympoTIC'03.Joint 1st Workshop on Mobile Future and Symposium on Trends in Communications. Bratislava， Slovakia. IEEE， 2003：51-54.

[21] GEZICI S，MOLISCH A F，POOR H V，et al.The trade-off between processing gains of impulse radio systems in the presence of timing jitter[C]//2004 IEEE International Conference on Communications.Paris，France.IEEE，2004：3596-3600.

[22] WIN M Z. On the power spectral density of digital pulse streams generated by M-ary cyclostationary sequences in the presence of stationary timing jitter[J]. IEEE Transactions on Communications，1998，46（9）：1135-1145.

[23] BALAKRISHNAN A.On the problem of time jitter in sampling[J].IRE Transactions on Information Theory，1962，8（3）：226-236.

[24] LIU B， STANLEY T. Error bounds for jittered sampling[J].IEEE Transactions on Automatic Control，1965，10（4）：449-454.

【通聯编辑：唐一东】