渐进式分组狩猎的灰狼优化算法及其工程应用
袁钰婷 高岳林 左汶鹭
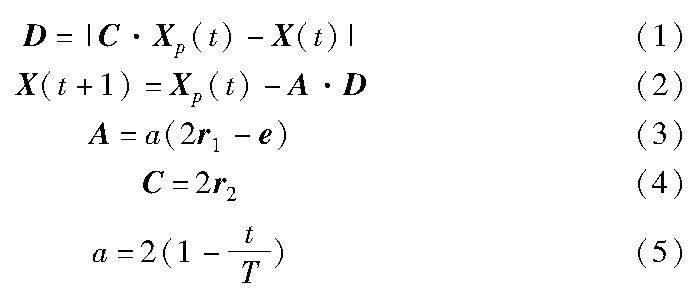

摘 要:针对灰狼优化算法(GWO)在求解复杂优化问题时存在后期收敛速度慢、易陷入局部最优的不足,提出了一种渐进式分组狩猎的灰狼优化算法(PGGWO)。首先,设计了非线性多收敛因子以增强全局勘探能力、避免局部最优;其次,提出了渐进式位置更新策略,该策略引入长鼻浣熊的包围策略和动态权重因子,前者在提高收敛精度和速度的同时避免局部最优,后者则动态地提升算法的收敛速度及全局寻优性能;最后,通过与标准GWO、4个GWO先进变体以及4个竞争力较强的新型进化算法对比,验证了PGGWO的有效性和先进性。在24个Benchmark函数和3个实际工程优化问题上的实验结果表明,PGGWO在收敛精度和收敛速度上具有明显优势,并且对约束优化问题也是有效的。
关键词:灰狼优化算法;渐进式分组狩猎;多收敛因子;动态权重因子;工程约束优化
中图分类号:TP301.6 文献标志码:A 文章编号:1001-3695(2024)05-019-1409-11
doi: 10.19734/j.issn.1001-3695.2023.10.0449
Grey wolf optimization algorithm based on progressive grouping
hunting mechanism and its engineering applications
Abstract:Focus on the shortcomings of the GWO in solving complex optimization problems, such as slow convergence speed and easy to fall into local optimum, this paper proposed a grey wolf optimization algorithm based on progressive grouping hunting mechanism(PGGWO). Firstly, it designed the nonlinear multi convergence factors to enhance the global exploration ability and avoid local optimum. Secondly, it proposed a progressive location update strategy. The strategy introduced the encirclement strategy of coati and dynamic weight factors, the former avoided local optimum while improving convergence accuracy and speed, the latter dynamically improved the convergence speed and global optimization performance of the algorithm. Finally, through comparing with GWO, 4 advanced GWO variants and 4 new with strong competitiveness, the experiment verifies the effectiveness and advancement of PGGWO. The experimental results on 24 Benchmark functions and 3 practical engineering optimization problems show that PGGWO has obvious advantages in convergence accuracy and convergence speed, and is also effective for constrained optimization problems.
Key words:grey wolf optimizer(GWO); progressive grouping hunting; multi convergence factor; dynamic weighting factor; engineering constrained optimization
0 引言
近年來,优化技术已被广泛应用于工程设计[1]、金融工程[2]、信息科学[3]和经济管理[4]等领域。然而,全局优化问题模型通常具有强非线性、复杂、高维的搜索空间,基于梯度信息的传统优化方法难以有效求解,因此不再适用。在过去的半个世纪里,群智能优化算法因其原理简单、实现容易、能以较大概率收敛到问题最优解等特点,在优化领域中被广泛应用[5]。常见的群智能优化算法有遗传算法(genetic algorithm,GA)[6]、粒子群优化算法(particle swarm optimization,PSO)[7]、差分进化算法(differential evolution,DE)[8]、生物地理学优化算法(biogeo-graphy-based optimization,BBO)[9]、灰狼优化算法(GWO)[10]和白鲸优化算法(beluga whale optimization,BWO)[11]等。虽然群智能优化算法不能保证在所有情况下都能得到最优解,但是它们能够在可接受的时间内提供合理的解[12],如非确定性多项式时间(NP-hard)问题[13]。尽管群智能优化算法由于参数少且通用性好而得到了广泛的应用,但其避免局部最优的能力仍然不足[14]。此外,随着现实世界优化问题日益趋向高维、复杂和多样化发展,经典的群智能优化算法难以有效求解高维优化问题。
GWO是由澳大利亚学者Mirjalili等人[10]依据自然界中灰狼种群严格的社会等级机制和狩猎行为提出的。首先,灰狼种群被划分为四个社会等级;其次,灰狼种群根据前三等级灰狼前一次迭代的位置进行更新。按照此过程不断循环进行位置移动,直至找到合适的猎物。GWO具有全局勘探能力强、调节参数少、原理简单、容易实现等优点。在单峰和多模态无约束基准函数的情况下,GWO的寻优性能明显优于GA、PSO和DE等,在未知的搜索空间中具有较为高效的性能。当对复合函数进行测试时,它能够高度避免局部最优。因此,研究发现GWO更适合解决现实世界的问题[15]。但是从GWO本身的进化机制来看,该算法在解决某些优化问题时仍存在后期收敛速度慢、易陷入局部最优的不足[16]。针对这些不足,國内外学者对其进行了改进,主要包括对灰狼种群初始化、算法参数、搜索机制进行改进和设计新的混合算法两方面。
王敏等人[17]利用反向学习策略产生初始灰狼种群以维持群体多样性,并对当前最优灰狼个体进行变异操作以减少算法出现早熟收敛的可能性,但生成反向种群的过程会增加不必要的计算量,且变异操作会出现将原本优秀的个体变差的可能性。Yu等人[18]则对此加以改善,以跳跃率Jr对部分个体生成反向解,并择优组成初始种群。Chen等人[19]通过随机添加自适应权重和搜索策略增强全局勘探能力,然而其收敛速度和精度需要提高。随后,Mafarja等人[20]提出了多种勘探与开发策略,增强了GWO算法的全局搜索和局部搜索能力,但划分多个阶段并使用其他算子将显著增加计算成本。Wang等人[21]提出了一种自适应平衡的GWO寻找高维分类的最佳特征子集,该算法采用自适应方法提高了算法的全局勘探能力。在算法融合上,刘紫燕等人[22]提出了一种基于杂交策略的自适应GWO,通过引进遗传杂交策略和蝠鲼觅食策略,有效提升了算法的收敛精度及全局寻优性能。李全耀等人[23]结合教与学优化算法(teaching-learning-based optimization, TLBO)[24]和PSO加快了算法的收敛速度,但其全局勘探能力仍有待加强。谢少鹏等人[25]针对GWO存在的局部搜索精度差的问题,从初始种群、收敛因子等方面着手,改善GWO的局部搜索能力及收敛速度,但其全局寻优性能有待提高。
虽然许多研究在一定程度上改善了GWO的性能,但在求解复杂多峰函数和某些工程应用时,后期收敛速度慢、易陷入局部最优的问题依然存在。
针对以上问题,本文提出了一种渐进式分组狩猎的灰狼优化算法(grey wolf optimization algorithm based on progressive grouping hunting mechanism, PGGWO)。
与现有文献相比,本文的贡献和主要创新点包括:a)设计非线性多收敛因子策略以模拟灰狼种群的包围与狩猎过程,避免局部最优;b)提出了一种渐进式位置更新策略,将灰狼种群分为两组,第一组灰狼学习长鼻浣熊的包围策略,另一组灰狼则遵循不同的学习率,动态地向猎物逼近,使得算法在提高收敛速度的同时增强全局勘探能力、提升算法精度。
1 标准GWO
GWO将灰狼种群的社会等级分为α、β、δ和ω四种。其中,第一层为α狼,是群体中的领导者,也是最优解;第二层为β狼,协助α狼进行决策,是次优解;第三层为δ狼,负责侦查、看护、放哨等事务,是第三最优解;最底层的为ω狼,听从前三等级的狼的领导。此外,GWO通过模拟灰狼种群的狩猎过程实现优化搜索的目的。
1.1 包围猎物
在追踪目标猎物时,灰狼通过式(1)(2)的位置更新方程围攻猎物。
其中:D表示猎物与灰狼之间的距离向量;|·|表示两个位置向量对应分量作差后取绝对值所得的向量;Xp(t)表示猎物的位置;X(t)为第i只灰狼的位置,i∈N,N为种群规模;X(t+1)为t+1时刻第i只灰狼的更新位置,t为当前迭代次数, T为最大迭代次数;A和C为两个系数向量,共同平衡算法的勘探和开发能力;r1和r2为[0,1]的随机向量;e为单位向量;收敛因子a又称为距离控制参数,随着迭代次数的增加,a从2线性减少到0。
1.2 跟踪猎杀猎物
为了模拟灰狼的狩猎行为,假设α、β和δ狼更了解猎物的潜在位置。于是保存迄今为止取得的三个最优解决方案,并利用这三者的位置来判断猎物所在的位置,同时强迫其他灰狼个体依据最优灰狼个体的位置来更新其位置,逐渐靠近猎物。灰狼个体的位置更新公式如下:
其中:Dα、Dβ和Dδ分别代表灰狼个体与α、β和δ狼之间的距离向量;Xα(t)、Xβ(t)、Xδ(t)分别表示α、β、δ狼的当前位置;X1(t)、X2(t)、X3(t)是ω狼分别根据α、β和δ狼的位置生成的指导位置,表示ω狼向α、β和δ狼靠近的方向和步长;Xi(t+1)为第i只灰狼根据α、β和δ狼的指导位置调整后的下一时刻的更新位置;A1、A2和A3的计算同式(3),C1、C2和C3的计算同式(4),表示狼群不同个体的勘探与开发,它们都是系数向量。
1.3 搜索和攻击猎物
GWO算法设计了A和C两个系数向量,以平衡勘探和开发能力。当|A|<1时,狼群向猎物发起攻击(陷入局部最优),当|A|>1时,强迫灰狼与猎物分离,希望找到更合适的猎物(全局最优解)。并且由式(3)可知,A的大小取决于收敛因子a的大小。组件C则用来帮助发现新的解决方案,表示灰狼所在的位置对猎物影响的随机权重。C>1表示影响权重较大,反之,表示影响权重较小,这有助于GWO算法更随机地进行搜索,同时可在优化过程中避免陷入局部最优。
GWO算法通过模拟灰狼种群搜索、包围和攻击猎物三个阶段的狩猎过程实现优化搜索的目的。标准GWO算法的流程如图1所示。
2 改进的GWO算法
2.1 非线性多收敛因子
GWO算法利用随机值大于1或小于-1的参数A来迫使灰狼与猎物分离,以模拟种群的分散程度。协调GWO全局勘探能力和局部开发能力的关键在于参数A的大小。随着迭代次数的增加,a从2线性减少到0,其对应的A值也在[-a,a]变化。因此,a的取值决定着算法的全局勘探能力和局部开发能力。然而,灰狼种群的包围与狩猎过程非常复杂,GWO原有的线性控制参数策略不能很好地模拟这一过程,导致算法易陷入局部最优。先前的研究已证明,使用非线性调整可以更好地平衡GWO的勘探与开发[26]。因此,近年来大多数国内外学者采用非线性控制参数方法进行改进。例如,文献[27]提出了二次函数控制参数的GWO,文献[25]提出了余弦控制参数的改进GWO的仿真策略。上述大多数改进都是对单一的收敛因子进行改进,忽略了灰狼种群社会等级制度的灵活性。为使算法的搜索更加灵活,文献[28]提出一种竞争引导策略来更新个体位置,该策略使用了三种不同的余弦收敛因子。本文受到文献[28,29]的启发,提出一种非线性的多收敛因子策略以便更好地提高勘探能力、避免局部最优。具体公式如下:
原算法的线性收敛因子a和本文改进的余弦收敛因子a1对勘探和开发的影响如图2(a)(b)所示,纵坐标均由式(3)根据对应的收敛因子计算。线性递减的收敛因子a导致|A|在迭代中期之后保持小于1,这在一定程度上限制了种群在迭代中后期的全局勘探能力;而非线性递减的a1使|A|在迭代的中后期保持大于1,这意味着使用该非线性余弦收敛因子可以让种群保持更长时间的勘探能力,并有更多机会跳出局部最优。
另外,考虑到α、β、δ狼所代表的解具有不同程度的优越性,从而对种群位置更新产生不同的影响,本文提出了基于余弦和正弦两种不同的非线性收敛因子。方式如下:a)对于α和β狼,使用式(13)所示的余弦收敛因子a1,目的是使a1的值和经典GWO收敛因子a的取值一致,从2减小到0,以确保α和β狼在引导狩猎过程中的领导地位;b)对于δ狼,使用式(14)所示的正弦收敛因子a2,以使其取值由1非线性增长到2,对应的|A|便更有可能超出[0,1],效果如图2(c)所示。种群在更新过程中与δ狼保持距离,δ狼则引导种群进行解空间的大范围搜索,从而为有效地提高算法的全局勘探能力提供保证。
本文提出的两种非线性收敛因子与式(5)所示的控制参数随迭代次数的变化曲线如图3所示。由图3可知,在迭代过程中,标准GWO算法的控制参数a从2线性下降到0,而本文设计的两个控制参数a1和a2的曲线斜率是不断变化的。其中,a1从2非线性下降到0,迭代前期缓慢,约350代才减小到1。因此更有可能使|A|>1,扩大α、β狼的搜索范围、增强勘探能力。迭代后期,a1迅速减小以加速收敛、增强局部开发能力。a2则在遵循社会等级制度的前提下,由快到慢地從1非线性增加到2,以使δ狼在某种程度上能够发现更多猎物,避免局部最优。这两种收敛因子搭配使用,使得灰狼种群能够更好地进行勘探和开发,大大减少了陷入局部最优的情况。
2.2 渐进式位置更新策略
标准GWO在求解复杂优化问题时存在后期收敛速度慢的问题。除此之外,在寻优至中后期时,整个灰狼种群均趋向于向α、β、δ狼所在的位置移动。一旦α、β、δ狼困在局部范围内搜寻目标猎物,整个灰狼种群将无法继续实现种群的进化[29]。基于此,受文献[30]中长鼻浣熊狩猎行为的启发,本文提出了一种渐进式位置更新策略。首先将灰狼种群分为两组,前一半灰狼种群在α狼的带领下移动到搜索空间中的不同位置,广泛搜索并包围猎物;随后,后一半灰狼种群根据α、β和δ狼的指导位置快速逼近并攻击猎物,以加速收敛。该策略通过广度与深度的结合实现在问题空间上勘探与开发的适当平衡。
2.2.1 包围策略
在长鼻浣熊的勘探阶段[30],群体中的长鼻浣熊兵分两路,其中一部分浣熊采用的包围策略可以使长鼻浣熊移动到空间中的不同位置,很好地展现了长鼻浣熊的全局勘探能力[31]。基于此,本文将该策略融入灰狼种群的部分狩猎行为,使得算法在扩大搜索范围的基础上提高收敛的速度和精度。数学模型为
Xi(t+1)=Xi(t)+r×(Xbest(t)-I×Xi(t))(15)
其中:r表示各分量取值为[0,1]的随机实数;I为一个随机整数,来自集合{1,2};Xi(t)为第i只灰狼个体在t时刻的位置;Xbest(t)为当前种群中最佳个体(即α狼)的位置;Xi(t+1)为第i只灰狼个体在t+1时刻的位置。
每次迭代时,该部分的位置更新过程将不再根据三只头狼指导位置的平均值确定,而是通过灰狼个体当前位置和α狼的位置进行位置更新。这样便更靠近最佳个体(α狼)的位置,提高了收敛速度。除此之外,r与I的双重扰动使得灰狼种群在α狼周围随机游荡,扩大了搜索范围,避免了局部最优。这可以使种群进一步向着全局最优解方向进化,提高收敛精度。
2.2.2 动态权重因子
若α狼不是全局最优,随着灰狼个体向三个最优搜索代理位置靠拢时,整个算法也将陷入局部最优,难以找到真正的最优解[32]。因此,本文引入一种基于最优个体位置向量模值的比例权重,通过权重因子的不断变化,动态调节算法的全局勘探能力和局部开发能力,加速算法收敛。
GWO算法中三只头狼的位置是动态变化的,则权重因子也应随着寻优过程非线性调整变化。因此,近年来许多学者根据头狼的指导位置或利用适应度值对位置更新公式进行了有效改进。比如利用指导位置改进的文献[19,33]以及利用适应度值改进的文献[34]等。标准GWO算法通过计算三只头狼指导位置的平均值来更新灰狼位置,如式(12)所示。本文为了加强当前迭代过程中最优个体的作用,对式(12)进行了改进,如式(19)所示。
其中:‖Xα(t)‖、‖Xβ(t)‖和‖Xδ(t)‖表示t时刻三个最优个体(α、β和δ狼)位置的向量模值;w1(t)、w2(t)和w3(t)为基于步长欧氏距离的比例权重,分别代表其余灰狼个体对α、β和δ狼的学习率,用于控制位置更新时种群个体向α、β和δ狼前进的步长和方向。文献[35]从理论角度对运用基于步长欧氏距离的比例权重效果进行了研究验证,表明权重因子在算法的每一次迭代中不断变化,使得三只头狼能够动态地指导狼群前进。由于α狼不一定是全局最优点,易陷入局部最优,本文利用此特点,在文献[35]的理论基础上设计了基于最优位置的权重因子w1(t),该权重因子的大小主要取决于α狼的当前位置,而α狼不一定是全局最优,所以每次迭代中的w1(t)也不一定小于w2(t)和w3(t)。同理,w2(t)和w3(t)的大小也在不断变化。经过不同程度的学习,灰狼个体可以动态调节向头狼前进的步长和方向至迭代结束。因此,将灰狼个体的位置更新公式改进如式(19)所示,该策略通过引入动态权重解决了算法收敛速度慢以及易陷入局部最优的问题。
综上,与经典GWO算法的主要区别是:渐进式位置更新策略将灰狼种群分为两组,且不再全程依照α、β和δ狼的位置更新迭代。种群中一半的灰狼仅隶属于α狼,而不再受α、β和δ狼的共同领导,因此加快了收敛速度;另一半灰狼则遵循不同的学习率,动态地向猎物逼近,提升了算法的全局寻优性能。此外,在每次迭代过程中,两组灰狼群体按照不同的更新方式并行前进。又因受动态变化的权重因子w1(t)、w2(t)、w3(t)与随机扰动因子r、I的影响,使得算法在加快收敛速度的同时避免局部最优,提升了算法的收敛精度。
算法1 PGGWO算法
2.3 复杂度分析
本节对PGGWO算法的计算复杂度进行分析,并用Big-O表示法表示。设灰狼的种群规模为N,问题的维数为D,最大迭代次数为T。对于GWO算法,每次迭代的初始化阶段需O(N×D),适应度函数评估需要O(N),α、β、δ三只头狼的选择需要O(N),位置更新过程需要O(N×D),总的计算复杂度为O(N×D×T)。而对于PGGWO算法,其每一次迭代,种群初始化需要O(N×D),适应度函数评估需要O(N),α、β、δ三只头狼的选择需要O(N),两阶段的位置更新策略各需要O(N×D/2)。因此,每次迭代总的计算复杂度为O(N×D),那么整个迭代的计算复杂度为O(N×D×T)。由此可见,本文PGGWO在整体上并没有增加计算复杂度,与标准GWO算法的计算复杂度相同。
2.4 收敛性分析
算法的收敛性是指某个算法能否在迭代时间趋于无穷的假设下,最终找到问题的全局最优解。
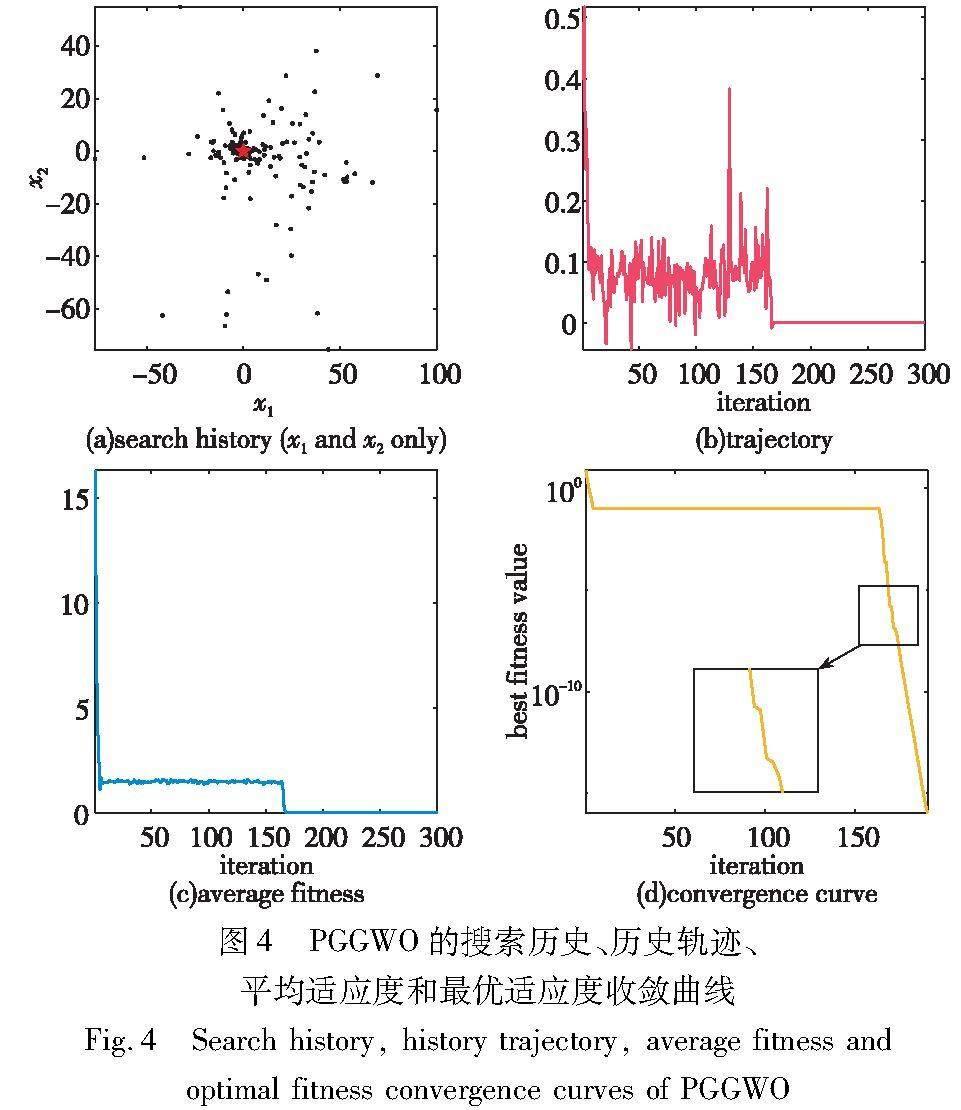
通过第3章的数值实验与分析可知,PGGWO算法在绝大多数测试问题上都能收敛到零误差均值,即找到了全局最优解。为了更直观地对算法收敛行为进行综合分析,本节给出了如图4所示的PGGWO在多峰函数f18(表1)上的搜索历史、轨迹、平均和最优适应度值收斂曲线图。
图4(a)展示了灰狼种群的搜索历史,可以呈现搜索空间中每个个体的分布。其中黑色的圆点代表种群个体的分布,红色五角星状的点代表搜索空间中的全局最佳位置(参见电子版)。可以看出,大多数个体都分布在全局最优解的周围,说明该算法具有良好的勘探能力,能够在搜索空间中更准确地确定有希望的搜索区域。为了更直观地展示搜索空间中个体勘探和开发的顺序,本节以第四只狼为例画出了其轨迹图,如图4(b)所示。首先存在突变行为,然后算法逐渐收敛到全局最优,可以扩大迭代中的随机搜索范围,保证勘探和开发之间的平衡。从图4(c)(d)可以看出,PGGWO算法在迭代中一直在收敛,逐渐接近最优解,表明
PGGWO具有良好的收敛能力。几次收敛停滞表明算法已陷入局部最优,但由于PGGWO的多收敛因子策略,使其又跳出了局部最优,说明该算法具有较好的避免局部最优的能力。
3 数值实验与分析
为验证PGGWO的收敛能力与寻优性能,证明其有效性和先进性,本章在24个Benchmark函数上进行数值实验。如表1所示, f1~f12为单峰函数, f13~f24为多模态函数,其中包含旋转、噪声等复杂函数,可以综合检验算法的寻优能力。
首先,通过与经典GWO对比,验证PGGWO的有效性;其次,将PGGWO分别与OGWO[18]、MSGWO[20]、AGWO[22]和new-GWO[24]四种近几年的GWO优秀变体进行比较;再次,与鲸鱼优化算法(whale optimization algorithm,WOA)[36]、BWO[11]、金豺优化算法(golden jackal optimization,GJO)[37]和蜜獾算法(honey badger algorithm,HBA)[38]四种竞争力较强的新型进化算法对比,以验证PGGWO的先进性;然后,通过对PGGWO的勘探开发百分占比分析进一步揭示算法性能优劣的真正原因;最后,将PGGWO应用于三个实际工程问题来检验算法的实用性。
3.1 实验设置
本文在Windows 10操作系统中完成,实验环境是Intel CoreTM i5-8500 CPU@3.00 GHz处理器,实验平台是MATLAB R2020a。所有算法的种群规模N均为50,且比较算法的参数均基于原文献。为避免偶然性,所有算法在每个函数上均独立运行50次,记录50次运行结果的误差均值(mean)和标准差(std),前者反映算法的收敛精度,后者反映算法的稳定性,因此误差均值是比较的重点。
3.2 PGGWO与标准GWO对比
将PGGWO与标准GWO在迭代次数T=500的条件下分别取D=30、50和100进行对比,实验结果如表2所示,加粗数据表示最优。可以看出,当D=30、50和100时,PGGWO在24个函数上均获得了最好结果,且在f1、f3、f5、f6、f8~f14、f17、f19、f22~f24这16个函数上得到了精确解(理论最优值0)。且在f2和f4函数上误差均值可达-200次方以上。
为了更加直观地比较PGGWO与GWO在不同基准函数上的收敛精度与收敛速度,绘制出两个算法在f1、f7、f10、f13、f19、f22这六个基准函数上的收敛曲线,如图5所示。其中,横坐标为灰狼种群迭代次数,纵坐标为算法独立运行50次后求得平均最小误差再取对数值。从图5(a)可以看出,在三个维度上,GWO的收敛速度比较缓慢且精度不高,误差指数约为-35;PGGWO拥有较好的收敛速度和精度,误差指数可在300次迭代内到达-300以上。在函数f7上,GWO与PGGWO收敛趋势十分相似,但相比之下PGGWO在迭代初期便迅速收敛,比GWO的误差均值降低了2个指数级。在函数f13上,当D=50和100时,PGGWO的收敛曲线出现了停滞现象,这表示算法到达局部最优;但在迭代中期,PGGWO可以有效跳出局部最优并快速找到全局最优解。这是因为PGGWO的非线性多收敛因子策略使δ狼化身侦察狼,并在浣熊包围策略的融入后扩大了种群搜索范围,增强了全局勘探能力,帮助群体找到更有可能存在最优解的区域并快速收敛。在函数f19上可以发现,当维数从30增加到100时,GWO的收敛速度和收敛精度逐渐变差,而PGGWO的收敛速度和精度一直保持不变,大约在40次迭代以内便可得到精确解。说明PGGWO可以有效提高GWO的收敛性能且具有良好的稳定性。综上,PGGWO的有效性可被证明。
3.3 PGGWO与近几年优秀变体对比
将PGGWO与OGWO、MSGWO、AGWO和newGWO这四种先进变体在24个Benchmark函数上进行对比。设置基准函数的维度D=200,最大迭代次数T=1000,运行50次。实验结果如表3所示,加粗数据表示最优结果。与其他算法相比,PGGWO在21个函数上均为最佳。其中,PGGWO在f1~f6、f8~f14、f16、f17、f19、f22~f24这19个函数上均找到了精确解。OGWO和newGWO虽然在函数f11和f23上得到了理论最优值0,并且在函數f20和f21上优于PGGWO,但是在其余20个函数上都不如PGGWO。稍具竞争力的是AGWO,其误差均值在函数f10、f11、f13、f19、f22和f23上均为零,并且在函数f18上略优于PGGWO,但都处于同一指数级,几乎无差别。相比之下,MSGWO更具竞争力,该算法在函数f10、f11、f13、f14、f19、f22和f23上与PGGWO一样都获得了精确解,并且在函数f20和f21上优于PGGWO,但在其余的15个函数上仍有较大差异。由此可见,虽然这些GWO变体在低维环境下具有优异的性能,但却不能有效求解高维全局优化问题,并不适合高维环境。相反,即使当D=200时,PGGWO仍然在19个Benchmark函数上精确地收敛到理论最优值,说明PGGWO具有良好的延展性,适用于高维优化环境。
为了清楚地比较PGGWO与四个变体之间的收敛过程,绘制了它们在不同Benchmark 函数上的收敛曲线。如图6所示,PGGWO具有最快的收敛速度,在迭代初期便有着明显的收敛效果,并且不易陷入局部最优。PGGWO在函数f1、f5和f24上的收敛精度及速度均明显优于其他四种对比算法。在函数f15上,PGGWO与AGWO、MSGWO在500次迭代之后的收敛精度十分接近,但仍能发现PGGWO的精度要优于其他两种算法,且收敛速度也十分明显。在函数f22上,PGGWO收敛更加迅速,几乎看不到收敛曲线。
观察所有收敛曲线图不难发现,PGGWO的收敛速度和精度均明显优于其他对比算法。这是因为在位置更新阶段加入了包围策略,使得前一半的灰狼种群无须综合三只头狼的指导位置进行更新,只接受α狼的领导,从而大大提高了算法的收敛精度。显而易见的是,PGGWO的收敛曲线在迭代前期便急速下降,这正是引入动态权重因子的缘故,使得后半部分的灰狼个体可以动态调节前进的步长和方向,从而加速算法收敛。
仅从误差均值和标准差这两个指标出发衡量各算法的优化效果还远远不够,需要进行统计检验以证明PGGWO具有显著的性能优势[39]。本文采用Wilcoxon秩和检验比较PGGWO与其他算法的差异。在5%的显著性水平下对算法独立运行50次的误差均值进行统计检验。结果如表3最后一行所示,“w/t/l”表示PGGWO优于/近似于/劣于相应的对比算法。
可以发现,PGGWO在24个函数上的性能明显优于其他对比算法。并且PGGWO的性能在f1~f9、f12、f15~f18、f20、f21和f24函数上显著优于四种GWO变体,仅在f18、f20和f21基准函数上稍逊于相应的对比算法,但误差均值相差不到一个指数级,在其余函数上获得了相近的结果。由此可见,PGGWO在这24个函数上具有整体有效性。
3.4 PGGWO与其他先进算法对比
将PGGWO与WOA、BWO、GJO和HBA四种近几年提出的竞争力较强的进化算法在D=200,T=1000上进行对比。类似地,为了避免偶然性,每个算法独立运行50次,并使用50次计算误差的平均值和标准差作为评价指标。表4显示了五种算法的数值实验结果,加粗数据表示最优结果。可以看出,PGGWO在22个Benchmark函数上获得了最小的误差均值,在19个Benchmark函数上获得了理论最优值,显然是五种进化算法中综合性能最好的。WOA在函数f10上也收敛到了与PGGWO相同的精确解,但在其他23个函数上均比PGGWO差;GJO在所有函数上均不如PGGWO,并且其误差均值没有一个收敛到零。相比之下,BWO和HBA展现了较强的竞争力,BWO虽然仅在f11上取得了零误差值,但在函数f20和f21上胜出,优于所有对比算法;HBA则在函数f9、f11、f13、f19和f23上均获得了零误差均值。尽管这些先进算法在低维问题上表现出了优异的性能,但在求解高维优化问题时其性能有所下降。相反,即使当D=200时,PGGWO在19个函数上仍然能精确地收敛到理论最优值。因此,本文的改进策略使GWO适用于高维优化环境,算法性能具有良好的延展性。
同样地,为了更好地评价PGGWO和对比算法,图7显示了五种算法在不同Benchmark函数上的部分收敛曲线。观察可得,PGGWO在不同的Benchmark函数上的收敛速度比其他进化算法更快,且不易陷入局部最优。特别地,对于函数f13、f22,PGGWO收敛迅速,几乎看不见收敛曲线。此外,可以发现在函数f18上PGGWO曾多次出现停滞现象,但在几次迭代之后便跳出了局部最优,继续进化。这是因为PGGWO采用了非线性的多收敛因子策略,使得种群的搜索范围扩大,全局勘探能力增强。
为了证明PGGWO比其他对比算法具有显著的性能优势,采用Wilcoxon秩和检验,结果如表4最后一行所示。可以看出,PGGWO的性能在函数f1~f8、f12、f15~f18、f20、f21、f24上显著优于其他四种进化算法;在函数f9~f11、f13、f14、f19、f22和f23上与对比算法获得相似的结果;仅在函数f20和f21上劣于对比算法。可见,即使与先进的进化算法对比,PGGWO也表现出了较强的竞争力。
3.5 勘探开发比分析
仅从误差的均值和标准差进行分析和讨论并不能揭示算法性能优劣的真正原因。勘探(exploration)和开发(exploitation)的平衡与否可以描述算法在迭代过程中是否达到最佳性能。勘探的目的是为了使算法具有尽可能多的局部最优解,开发的目的是为了使算法快速收敛到全局最优解。对勘探和开发的评价有助于更好地理解为什么某些算法在优化问题上表现优秀或低劣。为了进一步评估PGGWO,本节对其勘探和开发能力进行了测试,并对结果进行了讨论。
目前鲜有研究深入分析GWO的勘探和开发能力,为了提供可靠的理论依据,本节采用文献[40]提出的维度多样性测量方法评价勘探和开发。引入式(20):
其中:median(j)表示规模为NP的种群中所有个体第j维变量的中位数。由文献[40]可知,式(20)被用来检测维度多样性。种群内个体维度距离均值的增加代表勘探,减少代表开发。一旦计算出种群多样性,即可进一步判断种群在进化过程中的勘探占比和开发占比。勘探或开发的百分比测量可由式(21)定义。
为验证PGGWO平衡这两个状态的能力,并解释为什么PGGWO是有效的,本节在更为复杂、应用最广泛的CEC2014测试集上分析了PGGWO的勘探和开发行为。图8分别显示了GWO和PGGWO在部分测试函数上的勘探开发占比情况。
GWO在迭代前期就迅速以局部开发为主导,如图8(a)~(c)所示,这会导致算法前期的全局勘探不足,易陷入局部最优。而PGGWO的多收敛因子策略便较好地克服了这一缺点,使得算法在迭代前期能保持一定的勘探占比,如图8(d)~(f)所示。可以看出,PGGWO在迭代前期注重全局范围的搜索,寻找进化方向。迭代中期勘探和开发逐渐交替,迭代后期开发占比快速增加至100%,以加速向目标最优解移动。这是因为包围策略和动态权重因子可以使种群快速向目标位置移动,使种群在中后期相对接近最优解。这种情况下,不宜在大范围内进行探索,而应在小范围内寻找更优的候选解。因此,种群在进化后期倾向于局部开发。仔细观察便可发现,PGGWO在勘探与开发之间取得了良好的平衡,没有过度注重勘探,也没有过度集中于开发。并且从全局勘探到局部开发的过程是分阶段的,前期广泛搜寻猎物,后期快速逼近猎物,这也符合种群演化的特点。因此,该工作有效提高了GWO对勘探与开发的平衡能力。
3.6 工程应用
使用三个工程设计问题,通过与HHO(harris hawk optimization)[41]、AGWO、MSGWO、BWO和GJO比较目标函数是否最小,进一步验证PGGWO的实用性。PGGWO本身是针对无约束优化问题提出的,因此,求解约束优化问题时,需要对约束条件进行处理。根据进化计算中约束处理方法的研究进展,约束处理方法主要分为罚函数方法、可行性规则方法和多目标方法三类。其中,罚函数因其简单易实现而最为常用。为了简单起见,采用一种常见的惩罚方法處理约束条件:
其中:gi(x)是不等式约束,hj(x)是等式约束;p是不等式约束的个数,q是等式约束的个数,并且都是正的常数;η和λ为1或2。对于这种惩罚方法,当候选解违反任何约束时,目标函数值都会增加,将种群从不可行解推入可行域内。
3.6.1 压力容器设计问题
在该设计问题中,目标函数为压力容器的总成本,包括材料、成型和焊接成本[42]。如图9所示,压力容器的两端都有盖子封顶,头部一端的封盖为半球状。该优化问题包括四个决策变量:容器壁的厚度(Ts)、半球头部的厚度(Th)、内半径(R)、和圆柱截面的长度(L)。数学模型如式(24)所示。
将PGGWO在30次独立运行中针对压力容器设计问题获得的结果与HHO、AGWO、MSGWO、BWO和GJO五种对比算法比较,测试结果如表5所示。与其他算法相比,PGGWO在求解压力容器设计问题上获得了不错的结果。就最优解而言,PGGWO的优化效果要优于其他五种对比算法。
3.6.2 拉/压弹簧设计问题
弹簧是工业生产中的重要部件,影响其结构性能的因素很多,如图10所示。
拉/压弹簧的设计目的是在满足最小绕度、震动频率和剪应力的约束下,最小化拉压弹簧的重量[43]。该问题由三个连续的决策变量组成,即弹簧线圈直径(d)、弹簧簧圈直径(D)和绕线圈数(P)。数学模型表示如下:
式(25)中的目标函数是一个典型的多变量约束优化问题。为了说明PGGWO的设计效果,仍选择HHO、AGWO、MSGWO、BWO和GJO五种优秀算法应用于目标函数,并对优化结果进行了比较。各算法得到的弹簧设计参数和目标函数结果如表6所示。可以看出,PGGWO在设计拉/压弹簧问题上所得目标函数值最小,优于其他对比算法。
3.6.3 輪系设计
如图11所示,该问题的目的是使轮系的传动比成本最小化[44]。此问题有四个整数变量,其中Ta、Tb、Td和Tf表示四个不同齿轮的齿数。转动比为(Tb/Ta)·(Td/Tf)。数学模型如下:
表7给出了PGGWO与其他五种对比算法在轮系设计问题上的结果。可以看到,PGGWO的最优设计参数为(51,30,13,53),目标函数值为2.31E-11。结果表明PGGWO在寻找该问题的最优解方面也是非常有效的,并且优于其他对比算法。
综上所述,在三个复杂的工程设计优化问题上,PGGWO比其他对比算法取得了更好的优化效果。因此,PGGWO是一种值得推广和应用的先进算法,可以广泛应用于约束优化问题。
4 结束语
本文通过对经典GWO及其相关改进算法的分析和研究,提出了一种渐进式分组狩猎的灰狼优化算法。首先,设计了非线性多收敛因子策略,提高全局勘探能力、避免局部最优;其次,提出了渐进式位置更新策略,前一半灰狼个体采用浣熊的包围策略,后一半则根据设计的动态权重因子增强寻优效果。通过深度与广度的结合,提高了算法的收敛速度和全局寻优性能。通过在24个Benchmark函数上的对比实验发现,PGGWO的整体性能优于所对比的八种算法。在算法复杂度几乎不发生变化的同时,PGGWO避免了GWO易陷入局部最优的情况,提高了收敛精度和速度。但是在个别函数上,PGGWO仍然存在收敛精度不高、稳定性不够好的问题,未来将尝试在迭代后期加入变异扰动策略等进行改进。此外,在工程设计优化问题中,PGGWO可以获得较好的设计参数,说明PGGWO具有一定的实际应用价值。在今后的工作中,可以与图像处理、入侵检测、车辆路径、无线传感器网络等其他领域更复杂的优化问题相结合。
参考文献:
[1]Gu Xin,Wang Guan,Li Ning,et al. Application of response surface optimization technology and fluid-structure interaction in the enginee-ring design of torsional flow heat exchangers [J]. Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2022,236(12): 6607-6620.
[2]Kumar R R,Stauvermann P J,Samitas A. An application of portfolio mean-variance and semi-variance optimization techniques: a case of Fiji [J].Journal of Risk and Financial Management,2022,15(5): 190.
[3]Al-Odat Z A,Ali M,Abbas A,et al. Secure hash algorithms and the corresponding FPGA optimization techniques [J]. ACM Computing Surveys,2020,53(5): article No.97.
[4]Sriyakul T,Jermsittiparsert K. Optimal economic management of an electric vehicles aggregator by using a stochastic p-robust optimization technique [J]. Journal of Energy Storage,2020,32(12): 102006.
[5]Su Shen,Qin Yixiao,Yang Kaiyao. Structural optimization of unsymmetrical eccentric load steel box girder based on new swarm intel-ligence optimization algorithm [J]. International Journal of Steel Structures,2022,22(5): 1518-1536.
[6]Holland J H. Genetic algorithms [J]. Scientific American,1992,267(1): 66-73.
[7]Kennedy J,Eberhart R. Particle swarm optimization [C]// Proc of IEEE International Conference on Neural Networks. Piscataway,NJ: IEEE Press,1995: 1942-1948.
[8]Storn R,Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces [J]. Journal of Global Optimization,1997,11(4): 341-359.
[9]Simon D. Biogeography-based optimization [J]. IEEE Trans on Evo-lutionary Computation,2008,12(6): 702-713.
[10]Mirjalili S,Mirjalili S M,Lewis A. Grey wolf optimizer [J]. Advances in Engineering Software,2014,69: 46-61.
[11]Zhong Changting,Li Gang,Meng Zeng. Beluga whale optimization: a novel nature-inspired metaheuristic algorithm [J]. Knowledge-Based Systems,2022,251(9): 109215.
[12]Seyyedabbasi A,Kiani F. I-GWO and Ex-GWO: improved algorithms of the grey wolf optimizer to solve global optimization problems [J]. Engineering with Computers,2021,37(1): 509-532.
[13]Seyyedabbasi A,Aliyev R,Kiani F,et al. Hybrid algorithms based on combining reinforcement learning and metaheuristic methods to solve global optimization problems [J]. Knowledge-Based Systems,2021,223(7): 107044.
[14]Jiang Jianhua,Zhao Ziying,Liu Yutong,et al. DSGWO: an improved grey wolf optimizer with diversity enhanced strategy based on group-stage competition and balance mechanisms [J]. Knowledge-Based Systems,2022,250(8): 109100.
[15]Sharma I,Kumar V,Sharma S. A comprehensive survey on grey wolf optimization [J]. Recent Advances in Computer Science and Communications,2022,15(3): 323-333.
[16]Banaie-Dezfouli M,Nadimi-Shahraki M H,Beheshti Z. R-GWO: representative-based grey wolf optimizer for solving engineering problems [J]. Applied Soft Computing,2021,106(7): 107328.
[17]王敏,唐明珠. 一種新型非线性收敛因子的灰狼优化算法 [J]. 计算机应用研究,2016,33(12): 3648-3653. (Wang Min,Tang Mingzhu. Novel grey wolf optimization algorithm based on nonlinear convergence factor [J]. Application Research of Computers,2016,33(12): 3648-3653.)
[18]Yu Xiaobing,Xu WangYing,Li ChenLiang. Opposition-based learning grey wolf optimizer for global optimization [J]. Knowledge-Based Systems,2021,226(8): 107139.
[19]Chen Xiaojuan,Zhang Haiyang. Grey wolf optimizer with global search strategy [C]// Proc of International Conference on Electronic Information Engineering and Computer Science. Piscataway,NJ: IEEE Press,2021: 775-779.
[20]Mafarja M,Thaher T,Too J,et al. An efficient high-dimensional feature selection approach driven by enhanced multi-strategy grey wolf optimizer for biological data classification [J]. Neural Computing and Applications,2023,35(1): 1749-1775.
[21]Wang Jing,Lin Dakun,Zhang Yuanzi,et al. An adaptively balanced grey wolf optimization algorithm for feature selection on high-dimensional classification [J]. Engineering Applications of Artificial Intelligence,2022,114(9): 105088.
[22]刘紫燕,吴应雨,梁静,等. 基于杂交策略的自适应灰狼优化算法 [J]. 计算机应用研究,2022,39(1): 113-117. (Liu Ziyan,Wu Yingyu,Liang Jing,et al. Adaptive gray wolf optimization algorithm based on hybridization strategy [J]. Application Research of Computers,2022,39(1): 113-117.)
[23]李全耀,沈艳霞. 一种基于教与学的混合灰狼优化算法 [J]. 控制与决策,2022,37(12): 3190-3196. (Li Quanyao,Shen Yanxia. A hybrid gray wolf optimization algorithm based on the teaching-learning optimization [J]. Control and Decision,2022,37(12):3190-3196.)
[24]Rao R V,Savsani V J,Vakharia D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems [J]. Computer-Aided Design,2011,43(3): 303-315.
[25]谢少鹏,吴柏生. 基于改进灰狼优化算法的结构损伤识别 [J/OL]. 计算力学学报. (2023-03-09). http://cjcm.ijournals.net.cn/jslxxb/ch/reader/view_abstract.aspx?flag=2&file_no=202208220000001 & journal_id=jslxxb. (Xie Shaopeng,Wu Baisheng,Zhao Xiuting,et al. Structural damage identification based on improved gray wolf optimization algorithm [J/OL]. Chinese Journal of Computational Mechanics. (2023-03-09). http://cjcm.ijournals.net.cn/jslxxb/ch/reader/view_abstract.aspx?flag=2&file_no=202208220000001 & journal_id=jslxxb.)
[26]Mittal N,Singh U,Sohi B S. Modified grey wolf optimizer for global engineering optimization [J]. Applied Computational Intelligence and Soft Computing,2016,2016: article ID 7950348.
[27]李征南,秦江涛. 基于混合扰动的非线性灰狼优化算法 [J]. 软件工程,2023,26(7): 34-39. (Li Zhengnan,Qin Jiangtao. Non-linear grey wolf optimization algorithm based on hybrid perturbation [J]. Software Engineering,2023,26(7): 34-39.)
[28]Pan Hongyu,Chen Shanxiong,Xiong Hailing. A high-dimensional feature selection method based on modified gray wolf optimization [J]. Applied Soft Computing,2023,135(3): 110031.
[29]Yang Bo,Zhang Xiaoshun,Yu Tao,et al. Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine [J]. Energy Conversion and Management,2017,133(2): 427-443.
[30]Dehghani M,Montazeri Z,Trojovská E,et al. Coati optimization algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems [J]. Knowledge-Based Systems,2023,259(1):110011.
[31]Sammen S S,Ehteram M,Khozani Z S,et al. Binary coati optimization algorithm-multi-kernel least square support vector machine-extreme learning machine model (BCOA-MKLSSVM-ELM): a new hybrid machine learning model for predicting reservoir water level [J]. Water,2023,15(8): 1593.
[32]陳敏,陈晔,牛兴龙,等. 求解全局优化问题的多策略改进灰狼算法 [J]. 国外电子测量技术,2022,41(11): 22-29. (Chen Min,Chen Ye,Niu Xinglong,et al. Multi-strategy improved grey wolf algorithm for solving the global optimization problem [J]. Foreign Electronic Measurement Technology,2022,41(11): 22-29.)
[33]陳闯,Chellali R,邢尹. 采用动态权重和概率扰动策略改进的灰狼优化算法 [J]. 计算机应用,2017,37(12): 3493-3497. (Chen Chuang,Chellali R,Xing Yin. Improved grey wolf optimizer algorithm using dynamic weighting and probabilistic disturbance strategy [J]. Journal of Computer Applications,2017,37(12): 3493-3497.)
[34]Adhikary J,Acharyya S. Randomized balanced grey wolf optimizer (RBGWO) for solving real life optimization problems [J]. Applied Soft Computing,2022,117(3): 108429.
[35]王秋萍,王梦娜,王晓峰. 改进收敛因子和比例权重的灰狼优化算法 [J]. 计算机工程与应用,2019,55(21): 60-65,98. (Wang Qiuping,Wang Mengna,Wang Xiaofeng. Improved grey wolf optimizer with convergence factor and proportional weight [J]. Computer Engineering and Applications,2019,55(21): 60-65,98.)
[36]Mirjalili S,Lewis A. The whale optimization algorithm [J]. Advances in Engineering Software,2016,95(5): 51-67.
[37]Chopra N,Ansari M M. Golden jackal optimization: a novel nature-inspired optimizer for engineering applications [J]. Expert Systems with Applications,2022,198(7): 116924.
[38]Hashim F A,Houssein E H,Hussain K,et al. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems [J]. Mathematics and Computers in Simulation,2022,192(2):84-110.
[39]左汶鹭,高岳林. 基于随机邻域变异和趋优反向学习的差分进化算法 [J]. 计算机应用研究,2023,40(7): 2003-2012. (Zuo Wenlu,Gao Yuelin. Differential evolution algorithm based on random neighborhood mutation and optimal opposition-based learning [J]. Application Research of Computers,2023,40(7): 2003-2012.)
[40]Hussain K,Salleh M N M,Cheng S,et al. On the exploration and exploitation in popular swarm-based metaheuristic algorithms [J]. Neural Computing and Applications,2019,31(11): 7665-7683.
[41]Heidari A A,Mirjalili S,Faris H,et al. Harris hawks optimization: algorithm and applications [J]. Future Generation Computer Systems,2019,97(8): 849-872.
[42]Mohammed H,Rashid T. A novel hybrid GWO with WOA for global numerical optimization and solving pressure vessel design [J]. Neural Computing and Applications,2020,32(9): 14701-14718.
[43]Celik Y,Kutucu H. Solving the tension/compression spring design problem by an improved firefly algorithm [EB/OL].(2018-11-26). https://ceur-ws.org/Vol-2255/paper2.pdf.
[44]Ziat A,Zaghar H,Taleb A A,et al. Reliable and robust optimization of the planetary gear train using particle swarm optimization and Monte Carlo simulation [J]. SAE International Journal of Materials and Manufacturing,2021,15(1): 21-33.

