正交面齿轮传动的两类界线
赵亚平, 娄海青
(东北大学 机械工程与自动化学院,辽宁 沈阳 110004)
面齿轮传动源于“灯笼齿轮传动”[1],这是一种通过销齿啮合的拨挂齿轮副。现代正交面齿轮传动中,小轮为渐开线圆柱直齿轮,分度曲面是圆柱面;大轮为端面直齿轮,分度曲面是平面。在啮合传动的过程中,分度圆柱面在分度平面上做滚动和滑动。作为大轮的端面直齿轮,一般可用产形面与传动副中小轮齿面一致的刀具范成得到。按照机械传动的啮合理论[2-3],啮合界线是线共轭齿面偶[S1,S2]中,主动轮齿面S1瞬时接触线族的包络线,决定了主动轮齿面工作区的自然边界。通过对啮合界线进行深入系统的研究,可以为确定传动副技术参数提供理论依据,明确齿面参数的求解域,从而形成传动副的科学设计方法。同为偏置传动的锥蜗杆传动、圆柱蜗杆传动的啮合界线研究[4-7],已经充分证实了上述论断。从产形面与切齿啮合的相对运动出发,建立面齿轮齿面的奇点条件,按传动副的不同技术参数,研究齿宽系数、面齿轮内径的变化规律[8-11]。面齿轮内径取决于其根切特性,但是按其提供的内径公式设计面齿轮,往往不能切实保证面齿轮完全无根切[12],其他研究参见文献[13-16]。
本文通过研究啮合界线与曲率干涉界线得到了确定面齿轮内径的方法与计算公式。
1 正交面齿轮副的齿面方程
如图1所示,建立动坐标系σ1{O1;i1,j1,k1}与小轮固连,原点O1为小轮齿宽中点,k1沿小轮的轴线方向。小轮齿面为渐开线柱面,按图1所示几何关系,利用圆向量函数[17],可以写出小轮齿面S1的方程为:

图1 渐开线柱面形成机理示意
r1=rbe1(θ)-rbθg1(θ)+uk1
(1)
式中:u和θ为S1的曲纹坐标;u∈[-b1/2,b1/2],b1为小轮的齿宽;rb为小轮基圆半径。
从式(1)可求得偏导矢为:
r1u=k1,r1θ=rbθe1(θ)
(2)
从式(2)可以计算出小轮齿面S1的单位法向量n1,它指向小轮轮齿实体,n1为:
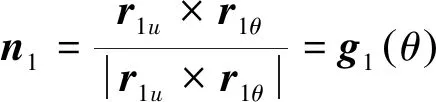
(3)
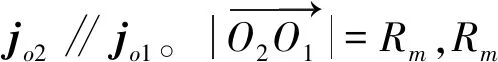
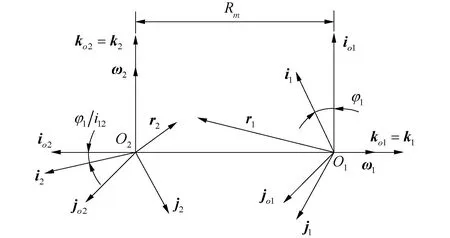
图2 描述面齿轮副啮合的坐标系

图3 轴截面内的面齿轮副
传动副啮合过程中,小轮齿面在静系σo1中形成单参数渐开线柱面族{S1},利用回转变换矩阵[3],从式(1)可以得到曲面族{S1}的方程为:
(r1)o1=R[ko1,φ1]r1=xo1io1+yo1jo1+uko1
(4)
式中φ1为小轮转角,而且,
从式(3)可以得到曲面族{S1}的单位法矢量为:
(n1)o1=R[ko1,φ1](n1)1=go1(θ+φ1)
(5)
取小轮角速度矢ω1=ko1,则大轮角速度矢量ω2=1/i12io1,参看图2,i12为面齿轮副传动比,从而传动副相对角速度矢为:
(6)
根据齿轮啮合理论[3],基于式(4)和式(6),面齿轮副的相对运动速度为:
(7)
从式(5)和式(7)得到正交面齿轮传动的啮合函数为:
(8)
式(8)对φ1求偏导数,即得到啮合界线函数为:
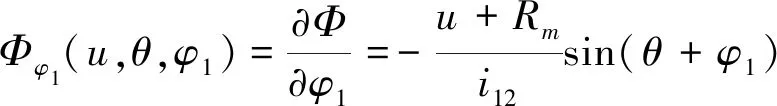
(9)
按图2所示的坐标变换关系,利用回转变换矩阵,从式(4)和式(8),在与面齿轮固连的动系σ2{O2;i2,j2,k2}中,可以得到面齿轮齿面S2方程:
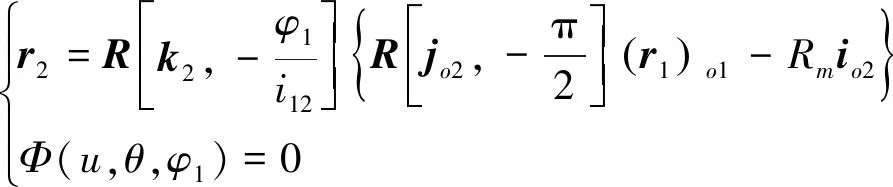
(10)
从式(10)中的啮合方程Φ=0可以解出:
(11)
把式(11)代入式(10),利用圆向量函数与球向量函数[17],齿面S2方程(10)改写为:
(12)
式中φ=θ+φ1。
2 啮合界线
2.1 啮合界线的方程及其性质
根据啮合理论,式(8)和式(9)中令Φ=Φφ1=0,可得到小轮齿面上2类界点[2]条件为:
sin(θ+φ1)=0
(13)
(14)
利用三角关系,从式(13)、式(14)可以求出:
u(1)=i12rb-Rm
(15)
u(2)=-i12rb-Rm
(16)
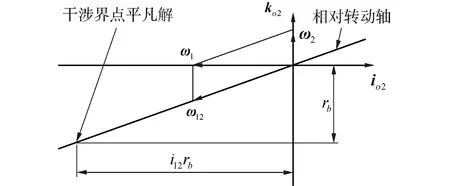
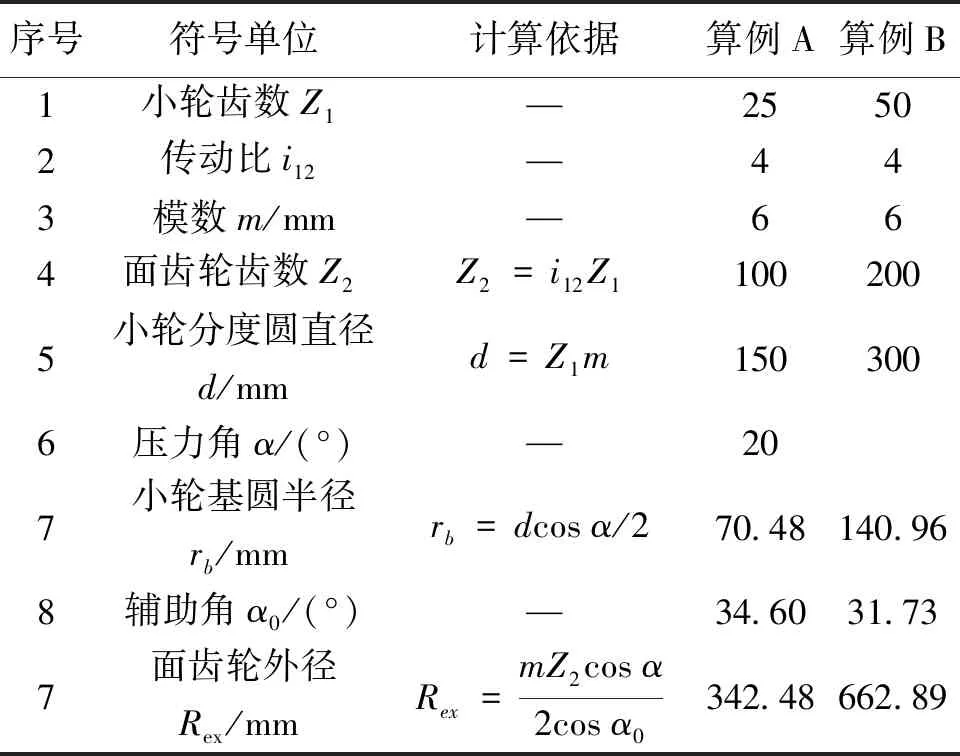
为限制面齿轮的轮廓尺寸,一般取i12rb-Rm<0,因而u(1)<0。又因从式(15)、式(16)可知u(2)-u(1)=-2i12rb<0,所以u(2) 假设0≤θ+φ1≤2π,把式(15)代入式(14)可以解得: φ1=π-θ (17) 式(1)中令u=u(1),可以得到小轮齿面上啮合界线的方程: r1(θ)=rbe1(θ)-rbθg1(θ)+(i12rb-Rm)k1 (18) 利用式(15),在坐标系{O1;xR1,yR1}中,面齿轮副的啮合界线方程可以表示为: (19) 式中xR1为常数小轮轴截面内,啮合界线垂直于小轮轴线的直线,参看图4。 图4 啮合界线和小轮齿面的相对位置关系 为了确保啮合界线不进入小轮齿面,按照式(19)应使得xR1≤-b1/2,又因为Rm=Rin+b1/2,其中Rin为面齿轮内径: Rin≥i12rb (20) 在啮合界线不进入小轮齿面这一前提下,面齿轮内径应满足的条件。在式(20)得到满足的条件下,i12rb-Rm<0。 为了保证啮合方程Φ=0有实数解、面齿轮齿面存在,从式(14)可以建立不等式: (21) 从而可以解得: u≥i12rb-Rm=u(1)或u≤-i12rb-Rm=u(2) (22) 根据近齿面和远齿面啮合界线分析,在轴截面坐标系{O1;xR1,yR1}中,绘制它们与小轮齿面的相对位置关系如图4所示。式(20)选定面齿轮内径Rin,近齿面啮合界线一侧的共轭区可以覆盖整个小轮齿面,理论上小轮可以全齿长参与啮合。 将式(13)、式(14)代入式(12),同时考虑到u+Rm=i12rb,即可得到面齿轮齿面上啮合界线共轭线的参数矢量方程为: (23) 式(23)表明,在垂直于面齿轮轴线k2的小轮基圆柱切平面内,啮合界线共轭线为一条渐开线,基圆半径为i12rb,在此基圆上的起始角度为(i12-1)π/i12。 建立面齿轮轴截面坐标系{O2;xR2,yR2},如图3所示,yR2轴沿面齿轮轴线,xR2沿面齿轮径向,根据面齿轮齿面方程(12)可以建立坐标转换关系: (24) 把式(17)代入式(4)中xo1和yo1的表达式,同时考虑到u+Rm=i12rb,并利用式(24),就可得到轴截面坐标系{O2;xR2,yR2}中,啮合界线共轭线的方程为: (25) 式(25)表明,在面齿轮轴截面内,啮合界线共轭线垂是直于面齿轮轴线的直线。 对式(12)求偏导矢,可得: (26) (27) 式(26)和式(27)做叉积得到: (28) (29) 式(29)是坐标平面(θ,φ)上S2的曲率干涉界线方程。此处建立面齿轮齿面奇点条件,较传统啮合理论中的方法[10]更简明。 因为式(29)是关于θ的一元二次方程,可得: (30) 把式(30)代入面齿轮齿面S2方程(12),就得到面齿轮副曲率干涉界线方程为: (31) 式(30)、式(31)表明面齿轮齿面上,曲率干涉界线一般存在2条。 为了确定曲率干涉界点,可以联立啮合方程Φ=0和式(29),建立非线性方程组: (32) 式中:-Ly为曲率干涉界点在面齿轮轴截面坐标系{O2;xR2,yR2}中的坐标,Ly>0。在求解方程组(32)确定一类界点时,Ly须按面齿轮齿高先行给定。 方程组(32)中未知量为θ、φ和u。当sinφ=0时,从式(32)可解得cosφ=-Ly/rb,故只能取定Ly=rb,从而cosφ=-1。又因为φ=θ+φ1∈[0,2π],所以在这种情况下,φ=π,如式(17)所示。将sinφ=0和cosφ=-1代入式(32),可以求得θ=0;将cosφ=-1代入式(32),可以求得u=i12rb-Rm。 以上实际上求得了非线性方程组(32)的一个平凡解:θ=0,φ=π,u=i12rb-Rm。据此,通过式(24)和式(25)可验证,此平凡干涉界点也位于啮合界线共轭线上,是干涉界线和啮合界线共轭线的交点。平凡干涉界点的共轭点,在小轮的基圆柱面上。因为基圆内无渐开线,此点可作为干涉界线的起始点。 将θ=0,φ=π,u=i12rb-Rm代入式(7),可以计算出相应干涉界点处的相对速度V12=0。把上述平凡解代入式(31),计算出平凡干涉界点在动系σ2中的径矢,经过坐标变换,可以得到此点在静系σo2中的径矢为: (33) 因为正交轴面齿轮副属相交轴传动,小轮大轮间的相对运动,为瞬时相对纯转动,其相对转动轴在平面内{O2;io2,ko2}通过点O2,且沿相对角速度矢ω12的方向,参看图5。因此根据空间解析几何,可在静系σo2中得出相对转动轴的方程为: (34) 图5 相对转动轴与干涉界点平凡解 式中作为分母的1, 0和1是瞬时转动轴所在直线方向矢量的分量,其中的“0”仅表示方向矢量的分量为0,并非以0做除数,进行除法计算,这样的表示在空间解析几何的文献中,十分常见。 把式(33)中干涉界点平凡解在静系σo2中的坐标代入式(34),方程得到满足,说明平凡干涉界点在相对转动轴上。 当sinφ≠0时,从式(32)可以解出: (35) 把式(35)代入式(32)得到: (36) 式中X=cosφ∈[-1,1]。 式(36)是关于X的一元五次代数方程,用Matlab中的roots函数,可以求得其全部根。选择在区间[-1,1]的实根作为X的合理值。数值计算的经验表明,这样的合理值一般有2个,分别对2条干涉界线。 按照以上求出的sinφ和cosφ,可以在区间[0,2π]确定角度φ,再根据从式(35)求得的θ角的值,就能计算出干涉界点处小轮转角φ1=φ-θ。另外,从式(32)又可求出,干涉界点处u=-i12rb/X-Rm。如此得到全部3个未知量(θ,φ1,u)后,就确定了面齿轮副的一个干涉界点。变动Ly值,就可以得到一系列干涉界点,把它们通过插值平滑连接,便得到干涉界线。 依照文献[12]确定表1中辅助角α0的值,以便计算面齿轮外径。给定Ly值得算例A、算例B如表2所示,按本文3.2节所述方法,取式(36)中X在-1附近的实根,计算各干涉界点,数值解结果亦见表2。根据这些数值结果,在面齿轮轴截面内{O2;xR2,yR2}绘制出图6中干涉界线Ⅰ。干涉界线Ⅱ对应X靠近1的实根,干涉界线Ⅰ上φ是第三象限角,干涉界线Ⅱ上φ是第四象限角。 表1 正交面齿轮副的主要参数 表2 干涉界线Ⅰ的数值结果 (算例A) 图6 面齿轮轴截面内曲率干涉界线和啮合界线共轭线 图6中齿面位于干涉界线Ⅰ和Ⅱ之间,既保证了齿面位于啮合界线可用一侧,又避让了干涉界线,还没有过分加大轮廓尺寸。这样就使得干涉界线Ⅰ大致位于面齿轮内端附近,干涉界线Ⅱ大致位于其外端以外。2条干涉界线都近似沿齿高走向。干涉界线Ⅰ上点1得自方程组(32)的平凡解。图6中啮合界线共轭线按式(25)绘出,反映出干涉界线Ⅰ上点1是干涉界线Ⅰ与啮合界线共轭线的交点。 干涉界线Ⅰ实际上控制了面齿轮内径Rin,使之不可过小,否则面齿轮容易发生曲率干涉。由于受到面齿轮齿顶锐化的限制[8,12],面齿轮外径Rex不可以过大,因而干涉界线Ⅱ通常远离面齿轮的齿面,对其进一步的讨论从略。由此可见,面齿轮发生曲率干涉的危险部位,在于其内端齿根位置。 如前所述面齿轮曲率干涉的危险部位,在其内端齿根,因此可在式(36)中取定Ly=r0=ra+c*m,求得相应干涉界点,以此干涉界点在轴截面坐标系{O2;xR2,yR2}中的横坐标xR2,为面齿轮内径。此处,ra为小轮齿顶圆半径,c*为小轮顶隙系数。这样就能保证干涉界线Ⅰ完全不进入面齿轮齿面,如图6所示。 按上述思路,借助啮合方程Φ=0、坐标转换关系(24)和式(36)可以建立关于(X,Rin)的代数方程组: (37) (38) 用Matlab中的roots函数,可以求得式(37)关于X的全部根,取其中大于-1且最接近于-1者,代入式(38),面齿轮内径Rin为: (39) 按式(36)的约定,式(37)中X=cosφ,据此利用三角关系,可以把式(37)改写为: (40) 式(40)是关于sinφ双二次方程,解之可得: (41) 利用式(41)和三角关系,就能把式(39)改为: (42) 基于干涉界点的计算经验可知:X=cosφ≈-1,参见表2。经此近似,从式(42)可得出内径Rin的近似计算公式为: (43) 从式(43)可知Rin>i12rb。 按表1中2个算例的数据,从式(43)计算出无根切最小内径Rin的近似值;从式(39)求得无根切最小内径的准确值,所得结果列于表3。该表中数据表明,近似解与准确解接近,不过一般略小。绘制图6所用内径Rin即按本节所述准确法求得。 表3 面齿轮无根切最小内径数值结果 事实上,面齿轮内端齿根部为刀顶形成的过渡曲面,而非范成齿面,用式(39)算出的Rin准确值作为面齿轮内径,可以充分保证面齿轮无根切,但得到的结构稍嫌不够紧凑。 1)通过建立的正交面齿轮传动啮合界线理论和曲率干涉界线理论,发现啮合界线是小轮齿面上的渐开线,其共轭线也是渐开线。 2)近齿面干涉界线存在于面齿轮齿的内端附近,基本沿齿高走向;近齿面干涉界线与啮合界线共轭线有一个交点,该点位于传动副相对转动轴上。 3)通过迭代求解,可获得内径准确值,导出的无根切最小内径估算公式便于设计中应用。
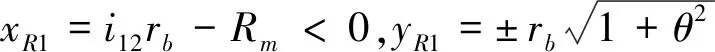
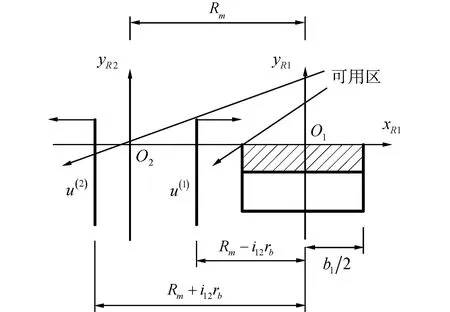
2.2 啮合界线共轭线
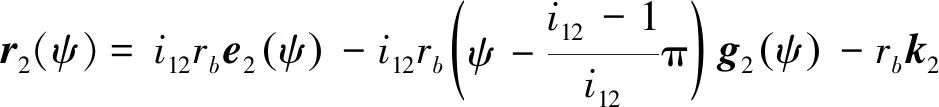
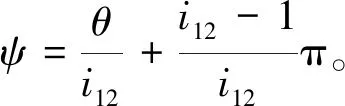
3 曲率干涉界线
3.1 曲率干涉界线方程


3.2 曲率干涉界点的计算原理

4 干涉界线的数值结果


5 面齿轮无根切最小内径的确定
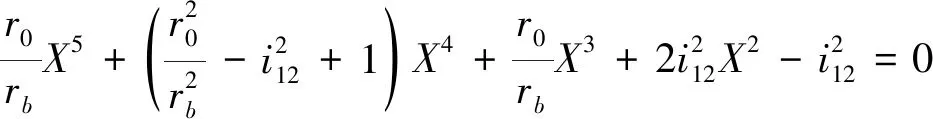


6 结论

