高层建筑深基坑支护结构位移动态监测方法

王贵美, 周建亮

(1.中国矿业大学 力学与土木工程学院,江苏 徐州 221116; 2.泛城设计股份有限公司,浙江 杭州 310015)

随着城市化建设不断发展,大部分国家的城市建筑用地紧张,为节约有限土地,提高活动空间,高层建筑以及超高层建筑理念受到青睐[1]。高层建筑在建设过程中,由于建筑的基础埋深较大,在挖掘深基坑时,会遭受周边原有建筑遮挡以及土方失稳等问题[2]。针对上述问题,为保障高层建筑的建设过程的安全进行,对高层建筑的深基坑支护结构位移数据实时监测,成为高层建筑建设过程中不可缺少的一部分。基于支护受力特性测量方法,根据深基坑支护密度确定土体测斜、竖向支护测斜、基坑阳角等参数,使用ABAQUS软件结合参数数值,模拟挖掘过程,完成深基坑支护监测[3-5]。传统该方法在计算挖掘规律时容易产生误差,影响监测效果。

本文通过分析高层建筑深基坑支护结构发生位移情况,得出了土压力分布及弹性地基梁力学参数变化情况是其主要影响因素,并计算变化值。采用遥感技术采集深基坑周围数据并进行降维处理,得到高层建筑深基坑支护结构位移动态监测的目标方程,建立动态变量矩阵,计算动态数据监测统计量,实现动态监测。

1 影响因素的量化分析

对高层建筑深基坑支护结构进行位移监测前,需要分析影响支护结构位移的各项影响因素。其主要因素为土压力分布及弹性地基梁力学性能。为此分别计算高层建筑深基坑支护结构所受实有土压力、附加土压力的分布,并计算弹性地基梁力学参数,为后续监测高层建筑深基坑支护结构位移打下基础。

1.1 土压力分布计算

在高层建筑的建设过程中,深基坑支护结构所承受的土压力主要来自外荷载压力,外荷载压力又分为实有土压力与附加土压力[6]。

1.1.1 实有土压力

由于深基坑土体挖掘过程中土的黏性不同需要用不同的计算方式。土体无较大黏性时使用库伦土压计算方法,土体黏性较强时,使用朗肯土压力计算法对土体进行计算,计算过程如下。

1)土体无粘性。

高层建筑在挖掘深基坑时,实有土压为:

(1)

式中:σa为设定主动的土压轻度;γ为深基坑填土厚度;z为基坑深度;q为坑后连续荷载分布;Ka为土压系数;φ为内摩擦角;δ为外摩擦角;β为基坑倾角。

2)土体强黏性。

高层建筑在深基坑支护过程中,若土体黏性较强,利用朗肯理论对黏性土体压力[7]计算为:

(2)

式中:σ′a为黏性土体压力;c为土体凝聚力。

1.1.2 附加土压力

高层建筑深基坑支护结构发生位移时,基坑挡墙会受到实有土压分为主动土压σa以及附加主动过程土压Δσa。静止土压与被动土压的差值称作被动过程土压σp,将其与附加主动过程土压Δσp进行整合统称为附加土压力,附加土体压力也分为砂土与黏土2类,具体计算结果如下所示:

1)砂土类附加土体压力计算结果为:

(3)

2)黏土类附加土体压力计算为:

(4)

式中:a、b、a′、b′为土体相关参数;σacr和σpcr为附加土体的极限位移。计算得出的主动、被动土体压力,完成对静止土压的获取:

σ0=(γz+q)K0

(5)

式中:K0为土压系数;σ0为计算出的静止土压。

1.2 弹性地基梁力学参数计算

将深基坑支护排桩看作竖置的弹性基梁,将深基坑内的土体与支撑支护结构之间的作用看作二力杆弹簧,土体对支护结构作用简化成主动土体压力,基坑挖掘面以下呈矩形分布结构,挖掘面以上为三角形分布形式。通过m法对深基坑内的被动区域进行计算,过程为:

fi=mizixi

(6)

式中:fi为设定第i个弹簧的反作用力;mi为比例系数;zi为弹簧的挖掘深度;xi为支护结构的水平移动值。

当支护结构侧重于土体压力与弹簧抗力时,使用m法获取支护结构挠曲微分方程:

(7)

式中:I为深基坑内挡墙的惯性截面矩阵;EI为支护结构的抗弯刚度;m为比例系数;zi为选定点至挖掘面的距离;eaik(zi)为土体压力分布函数;bs为计算宽度。

高层建筑建设从深基坑挖掘开始。挖掘过程中,如出现变形,会对深基坑进行支护[8],即建筑行业所谓的“先变形后支撑”。通过有限元方法,能够有效地利用节点位移值调整墙体的前期变形。所以在监测深基坑支护结构位移时,需将预加轴力转化成为相应的初始应变杆力完成计算。支护结构的初始应力值ε为:

ε=N(AEg)

(8)

式中:N为预加轴力;Eg为支护结构弹性模量;A为有限元函数。

2 动态监测

2.1 建立目标函数

根据上节参数计算,设计高层建筑深基坑支护结构位移动态监测方案,对采集到的深基坑周围数据降维处理。深基坑周围数据包括实有土体压力、黏性土体压力、土体极限位移、深基坑墙后填土厚度。在采集深基坑周围数据前埋好测点,获取各项静态数据的初始值。将位移传感器安装在沉降位移的测点上,测深传感器安装在深基坑墙后测点上,获取土体极限位移及深基坑墙后填土厚度数据,利用土压力计和孔隙水压力计,测试实有土体压力及黏性土体压力,获取实测数据。使用主成分分析(principal component analysis, PCA)方法对采集数据进行降维[9]处理。利用PCA算法构建增广矩阵模型,实现高维数据的线性无关转化,将原始的高维空间映射到一个低维空间,实现增广矩阵内元素的降维处理。

设定采样数据集为D,数据集中的数据量为X,建立的数据增广矩阵Xa,考虑数据之间的相关性使用PCA算法构建增广矩阵模型,过程为:

Xa=SPT+E

(9)

式中:S为得分矩阵;P为荷载矩阵;E为残差矩阵。基于式(1)建立的増广模型对采集数据进行降维处理,过程为:

(10)

式中:x为降维后的数据;Q为数据的统计量;∧为相交运算。

为提取数据的自相关动态变量特征建立高层建筑深基坑支护结构位移动态监测目标函数,过程为:

(11)

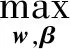
2.2 建立模型

设定位移影响因素为参数指标,结合建立的目标方程构建时间序列回归模型。将时间序列采样数据设定为zt,zt-1,…,z1,数据残差为et,自回归(autoregression,AR)系数设定为γj形式,设定数据集中第j个数据为zj,建立数据的自回归模型,过程为:

(12)

式中:C为AR系数矩阵;F为残差矩阵;zt为采样数据;XD+1为建立的模型;Z为数据矩阵;D为数据数量。模型在训练过程中,需要使用最小二乘法将F进行最小化处理。

2.3 建立动态变量矩阵

基于上述搜索的AR系数向量γ=(γ1,γ2,…,γD)T、投影向量w∈Rm×1,以及提取的动态潜变量s=Xw,其中,AR系数向量为监测数据自回归模型的时间序列向量,投影向量为监测数据投影到数据特征矩阵上的向量,对模型的最小残差进行计算,结果为:

(13)

式中:sj为第j个数据的动态潜变量;γj为系数;J为目标函数。由于变量的方差会对目标函数[10]带来影响,所以在计算过程中,需要设定相关约束条件s.t.[wTXTXw]=1。

基于上述计算结果,通过建立的模型,构建支护结构动态数据的动态变量矩阵,过程为:

Uk,D+1=[Uk,1,Uk,2,…,Uk,D]γk+Fk

(14)

式中:Uk,D+1为建立的动态变量矩阵;k为动态变量数据;γk为映射数据数据;Fk为模型残差变量。

再引入拉格朗日乘子,建立拉格朗日函数L,过程为:

L=‖XD+1w-z(γ⊗w)‖2+λ(1-wTXTXw)

(15)

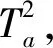
(16)

式中:α为置信阈值;Fα(K,n-K)为自由度;Λa为协方差矩阵;et为模型残差;n为数量总数量;K为动态变量;R为监测统计值。

算法流程如下:

1)采集数据并对数据进行降维处理,设定初始训练数据xi以及动态变量K;

2)通过对初始训练数据xi以及动态变量K的计算,获取目标函数,建立时间序列回归模型;

3)依据模型更新投影向量,并辨别γk与wk是否收敛。若未进行收敛则需通过模型继续更新γk与wk;

4)建立动态变量矩阵,计算动态数据监测统计量通过统计结果实现动态监测。

3 动态监测方法实验

为了验证动态监测方法的整体有效性,需要对此方法进行测试。分别采用高层建筑深基坑支护结构位移动态监测方法(方法1)、富水砂卵石地层深基坑开挖变形监测与数值分析(方法2)、软土深基坑组合开敞式支护数值模拟与监测分析(方法3)进行测试。在对深基坑支护结构进行动态监测时,控制3种方法的测试对象、测试环境及测试条件一致。

在对深基坑支护结构进行动态监测时,深基坑的位移轨迹、位移速率以及位移随时间变化曲线都会影响监测效果,将该3种影响因素作为3种性能检测指标,对3种监测方法进行测试。

1)位移轨迹测试。

在对深基坑支护结构位移监测时,产生的位移轨迹可以直观反映出位移监测的监测精度。设定支护结构位移监测5周时间,采用方法1、方法2以及方法3进行深基坑支护结构监测,对监测过程中的位移轨迹进行测试,测试结果如图1所示。

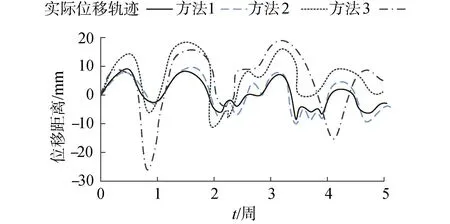
图1 不同监测方法的位移轨迹测试结果

分析图1可知,本文所提方法测试出的深基坑支护结构位移轨迹与实际的深基坑支护结构位移轨迹相接近,而方法2的支护结构位移轨迹与实际支护结构位移轨迹之间存在差距较大,方法3测试结果不理想。本文所提方法由于在深基坑支护结构位移监测前期,全方位分析了深基坑周边的土压力,获取了土压力分布,所以本文所提方法在进行深基坑支护结构位移监测时,能够有效测试出深基坑支护结构的位移轨迹,从而提高监测精度。

2)位移速率测试。

深基坑支护结构位移监测时,位移速率是否稳定会直接影响监测效果。采用方法1、方法2以及方法3进行支护结构动态监测,对3种监测方法监测出的位移速率进行测试,测试结果如图2所示。

图2 不同监测方法的位移速率测试结果

分析图2可知,本文所提方法测试出的深基坑支护结构位移速率与实际深基坑支护结构位移速率相接近,而方法2与方法3测试的深基坑支护结构位移速率与实际结果相差较大。由于本文所提方法在进行深基坑位移结构动态监测前,对影响基坑支护结构位移的深基坑弹性初始应力进行了具体分析,所以在进行深基坑位移结果动态监测时测试出的支护结构位移速率与实际深基坑支护结构位移速率相接近。通过该项测试能够证明本文所提方法在进行位移动态监测时的监测效果好。

3)纵向位移量测试。

基于上述测试结果,采用方法1、方法2以及方法3进行动态监测时,对深基坑支护结构纵向位移量(沉降量)进行测试,测试结果如图3所示。

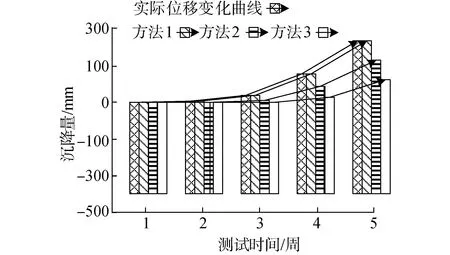
图3 不同方法的沉降量测试结果

分析图3可知,深基坑位移时间变化曲线随着时间的增加而上升。本文所提方法测试出的位移时间变化曲线与深基坑支护结构实际位移时间变化曲线相一致。而方法2与方法3在支护结构出现位移变化时,未能及时监测出深基坑的位移变化。

综上所述,经过测试本文所提方法监测到的深基坑支护结构位移轨迹与实际深基坑支护结构位移轨迹相接近、并且能有效测试出位移变化速率和位移时间变化曲线,由此证明本文所提方法在进行深基坑支护结构位移监测时的监测效果好。

4 结论

1)该方法能够有效监测高层建筑深基坑支护结构的位移动态。通过使用该方法进行监测,位移移动轨迹的监测误差较小,仅为0.1。该方法能够提供高精度的位移监测数据,接近实际位移情况。具有高精度的监测结果,能够准确地反映结构的实际位移量和沉降量。

2)该方法能够准确监测位移速率,位移速率保持在0.9 mm/d以下,并且与实际位移速率基本一致。可及时捕捉位移速率的微小变化,为及时采取应对措施提供依据。

3)该方法能够准确监测纵向位移量,纵向位移量达到202 mm,并且与实际沉降量一致。在纵向位移量的监测上具有较高精度,能够准确反映支护结构的沉降情况。

未来研究可进一步优化该方法的实时性和自动化程度,以适应更复杂的环境和条件,并拓展其在更多工程领域中的应用。