基于PSO-GA-BP 神经网络的土体参数反演

宋巍SONG Wei

（中国铁建投资集团有限公司，北京 100855）

0 引言

近年来，人口激增导致城市空间使用紧张、交通压力激增，为了缓解这一矛盾，城市空间正在向深度方向发展[1]。地下城市空间工程受场地地质、水文、周边建筑物、地下管线限制，需要准确、有效地预测其深基坑的变形[2]。目前数值模拟预测方法被广泛运用，获取准确的土体参数是确保预测精度的关键，而土体参数反演方法是获取参数的重要手段。

国内外学者对反演方法已经有了一定程度的研究。Gioda 等[3]通过利用单纯形法、拟梯度法以及Powell 法等优化方法，对岩土体的力学参数进行反演。Zhang 等[4]采用最小二乘法反演计算土体参数，利用反演后的土体参数预测挡土结构深层水平位移。程秋实等[5]采用粒子群算法结合支持向量回归机对基坑土体参数反分析，结果表明反演效果良好。

在土体参数反演领域，尽管BP 神经网络被广泛应用，但其存在网络结构构建难度大和收敛速度慢等缺点。为了解决这些问题，本文引入了PSO 算法和GA 算法，提出了PSO-GA-BP 神经网络土体参数反演模型，优化了BP 神经网络的结构和参数，从而提高模型的性能和准确性。

1 PSO-GA-BP 神经网络

尽管BP 神经网络在土体参数反演方面有着广泛的应用，但其存在网络结构构建难度大、收敛速度慢等缺点。同时，GA 算法在参数设计中的并行机制发挥不足、PSO 算法在处理高维数复杂问题时可能出现早期收敛[6]，为了进一步提高土体参数反演的效率和准确性，这些都是需要考虑和改进的问题。

基于此，本文提出PSO-GA-BP 神经网络土体参数反演模型，其同时具有粒子群算法及遗传算法的优点，而且优化了BP 神经网络中存在的问题。PSO-GA-BP 神经网络算法具体步骤如下，其流程图见图1。

图1 PSO-GA-BP 神经网络流程图

①确定神经网络输入层、输出层及隐含层的节点数量。

②对适应度函数进行求解，据此来判断个体和群体的极限值。

③随机选择每个粒子2/3 的位置，然后对粒子速度进行变异操作。

④经过变异后的粒子与相应的单个极限粒子、全局极限粒子继续进行交叉运算。

⑤将上述变异操作与交叉操作所得到的最新的速度信息与位置信息进行相加。

⑥重复步骤②～步骤⑤，选择最优的适应度函数值，并更新对应的权值与阈值。

⑦训练BP 神经网络，利用训练好的网络进行预测，得到最终的结果。

2 工程实例

2.1 工程概况

本文以武汉某地铁车站施工为例，本项目为地下三层14m 岛式车站，双柱横向五柱六跨箱型结构，车站主体结构采用盖挖逆作法。

本项目水文地质条件复杂，土层从上至下依次为杂填土、素填土、粘土、粉砂、卵石、强风化粉砂质泥岩、中风化粉砂质泥岩。

2.2 数值模型

本文选取基坑标准段建立模型，模型宽230m，长50m，深80m 模拟场地土层，标准段宽49.5m，开挖深度为28.8m。根据勘测结果，场地土层被划分为7 层。

土体模型采用实体单元，模型底部采用全约束，模型四周采用法向约束。围护结构地下连续墙采用板单元，厚度为1500mm；基坑顶板采用板单元厚度设为900mm，基坑底板采用板单元厚度设为2750mm，结构楼板采用板单元厚度设为400mm，混凝土钻孔桩采用梁单元直径2300mm，钢管混凝土立柱采用梁单元直径900mm。车站基坑ABAQUS 有限元模型如图2 所示。

图2 车站基坑标准段有限元模型

2.3 模拟结果

由图3 可知，测斜监测点号CX39，从实测数据上看，在基坑边缘处测得，围护结构深层水平位移最大变形量为8.77mm；在围护结构底端测得，最小变形量为0.30mm。从模拟结果上看，围护结构深层水平位移最大变形量为9.44mm，位于基坑边缘；最小变形量为0.32mm，位于围护结构底端。

图3 围护结构深层水平位移变化曲线

测斜监测点号CX35，从实测数据上看，在接近基坑边缘处测得，围护结构深层水平位移最大变形量为8.87mm；在围护结构底端测得，最小变形量为0.30mm。从模拟结果上看，围护结构深层水平位移最大变形量为9.53mm，位于基坑边缘；最小变形量为0.32mm，位于围护结构底端。

实测结果和模拟结果均表现为基坑边缘变形最大，沿深度方向逐渐减小，整体为前倾变形，且模拟结果显示了更大的最大位移和略微不同的最小位移值，最大误差为14.15%。

3 反演计算

3.1 反演模型参数的选取

鲁博铀分析了逆作法施工中主要参数对基坑变形的影响，在不考虑参数之间相关性情况下，单一因素中弹性模量对深基坑开挖围护结构变形最为敏感[6]。本文选择了土体的弹性模量作为待反演的参数，这一参数的选择对于围护结构中地下连续墙的性能研究至关重要，因为它直接影响了土体的变形和稳定性。又由于本文研究对象围护结构地下连续墙嵌入强风化粉砂质泥岩中，由2.3 节可知，该位置处实测与数值模拟结果误差较小。这意味着模型对于该位置的描述和预测较为准确，并且很好地反映了实际情况。

因此，本文反演的土体参数为强风化粉砂质泥岩以上的五层土体的弹性模量。其中参数选取范围取勘测结果±20%以内。

3.2 反演计算结果

使用MATLAB 建立PSO-GA-BP 反演模型，通过学习样本训练反演模型。将实测数据输入到反演模型中得到了前五层土体参数的反演结果，这些结果被整理在表1 中。从表格数据可以观察到，相对于初始值，反演结果进行了微小的调整，最大修正度为4.77%，最小修正度为0.37%。

表1 反演结果

为验证反演得到的土体参数的可靠性和适用性，采用土体参数反演结果的平均值，并将这些平均值作为输入，应用到ABAQUS 有限元模型中，用于模拟围护结构的情况。

由图4 可知，CX39 反演模拟结果水平位移曲线大部分位于实测结果上方，其绝对误差在1mm 以内，相对误差基本在5%以内。但是最大相对误差为9.91%，这可能是实测值异常造成的。

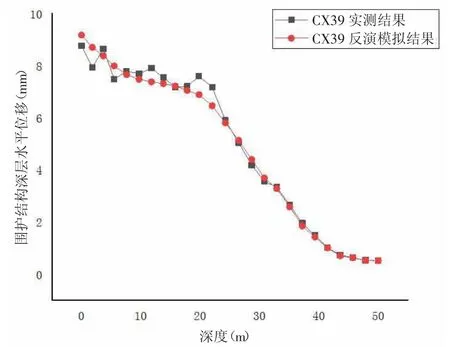
图4 CX39 反演模拟结果曲线图

由图5 可知，CX35 反演模拟结果水平位移曲线大部分位于实测结果上方，其绝对误差在1mm 以内，相对误差基本在5%以内。但是最大相对误差为12.08%，这是由于实测值异常造成的。

图5 CX35 反演模拟结果曲线图

由此可知，采用PSO-GA-BP 神经网络反演土体参数在模拟过程中取得了显著的效果，更接近于土体参数的实际值。忽略实测异常值，反演模拟结果能够达到工程要求精度。因此，PSO-GA-BP 神经网络反演模型能够为数值模拟提供更准确的土体参数。这对于提高预测结果的准确性和精度具有重要意义，为工程设计和分析提供了有力的支持和指导。

4 结论

本文以武汉某地铁车站深基坑施工为例，采用PSOGA-BP 神经网络反演方法获得了更为准确的杂填土、素填土、黏土、粉砂、卵石土体弹性模量，并将反演参数修正后模拟计算结果与实测结果以及原始模拟计算结果进行比较，得到如下结论：

①本文采用了ABAQUS 数值模拟方法对武汉某地铁车站的施工过程进行了模拟。模拟结果表明整体变形趋势与实测结果一致，显示该模拟方法具有某种程度上的预测能力。然而，与实测结果相比，模拟结果的数值精度不足，最大误差达到了14.15%。这意味着模拟结果在量化预测方面存在较大差异，不够准确。

②使用PSO-GA-BP 神经网络构建的反演模型成功地利用实测数据反演了土体参数，并对其进行微小的修正。相对于初始值，反演结果的最大修正度为4.77%，最小修正度为0.37%。

③将反演得到的参数结果输入到ABAQUS 模型中，对模拟计算进行修正。修正后的数值模拟计算结果更接近实测值，变形趋势与实测结果一致。尽管由于实测结果的不准确性，个别数据存在大约10%左右的误差，但大部分数据的误差在5%以内，修正后的模拟结果仍能够满足深基坑变形预测的需求。