基于TSP模型的企业配送线路优化设计
高一丹 张钰瑶 郑巧 徐成钰 赵萌
摘 要:随着现代社会经济的蓬勃发展,物流行业的发展逐渐成为一个国家现代化进程和综合国力的重要标志。物流行业的成本也渐渐成为一个热点问题,而配送成本在物流成本中占據较大的比例。文章以北京农夫山泉桶装水的配送路径问题作为研究目标,首先描述了研究背景与意义,并依次分析了国内外学者对于配送路径问题的研究现状,说明了本篇文章的研究内容;其次通过分析对北京农夫山泉实际走访与调研的结果,了解并提出北京农夫山泉配送过程中存在的一些问题;最后建立相对应的数学模型,利用Lingo软件中的TSP模型进行运算求解并分析得到结果,得出优化后的配送路径。
关键词:配送运输成本;配送路径优化;TSP模型
中图分类号:F252文献标识码:A文章编号:1005-6432(2024)14-0167-04
DOI:10.13939/j.cnki.zgsc.2024.14.040
1 北京农夫山泉配送线路现状
配送是整个物流活动系统中一个重要因素,产品可以通过配送产生更高的价值。而在北京农夫山泉的配送过程中,由于公司没有规定具体的配送路径,这就需要司机凭借自己的经验来做出判断。北京农夫山泉的配送方法是从配送中心向各个水站配送,车辆会经过每个水站然后返回配送中心。
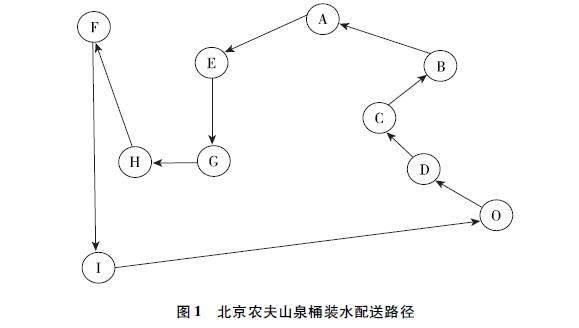
通过实地走访调查,了解到在一般没有规定的前提下,配送车辆司机自己所走的配送路径如图1所示,配送所走的路径是O-D-C-B-A-E-G-H-F-I-O,这样配送可以保证会经过所有水站并且返回到配送中心,在不加以考虑其他因素的条件下,配送路径的总里程为54.6km。
图1 北京农夫山泉桶装水配送路径
2 配送线路现存问题分析
2.1 存在迂回运输
配送水站H至配送水站I之间相距5.4km,通过配送路径图可知,从配送水站H到达配送水站I的时候中间先去到了配送水站F,还有就是配送水站I距离配送中心距离最远,可是返回时直接返回,由此可见,北京农夫山泉桶装水的配送路径中存在迂回运输。
2.2 存在过远运输
在配送点E、F、G、H四个配送点中存在多种路线可以选择,司机在配送这几个站点时选择了先去站点G再转到站点H,最后去到站点F,然后在返回时还要去到站点I,这就造成了整个运输过程中产生了过远运输。
2.3 存在空驶情况
在实际走访中,了解到在实际配送中,有时候运输组织人员为了紧急调运不得不将未装满的车辆进行紧急调运。北京农夫山泉在实际配送中,不能够对各个水站的存量进行统计,需要另发单车进行补货,这就会造成空车行驶和空车返程的问题。
3 北京农夫山泉配送路径优化模型构建
3.1 配送路径优化模型构建
3.1.1 具体问题描述
北京农夫山泉桶装水的配送路径优化问题可以描述为:从北京农夫山泉的配送中心出发,依次向其所有的水站进行货物配送,并最终返回配送中心。在这过程中会有很多的路线进行选择,需要找到配送里程最短的方案。
通过整理北京农夫山泉的数据,可以将路径优化看作是一个带权完全图G=(N,X)的问题,在这里面配送水站的地点可以用N表示,去到每一个水站的距离可以用X表示。用数学语言描述为:赋权图是G=(N,X),各水站之间的集合为N=(1,2,…,n),各水站之间的距离为dij(dij=∞,i,j∈N),知道各个水站和配送中心之间的距离,还有各水站之间的距离,这样就可以将这个问题转化为一个TSP问题,只需要求出经过所有配送水站之后的最短距离即可。
3.1.2 整理收集数据
文中以北京农夫山泉各个配送水站之间的配送路径优化为研究目标,在其中求得最优最短的配送路径。配送中心用字母O表示,其他九个配送水站依次用字母A、B、C、D、E、F、G、H、I表示。
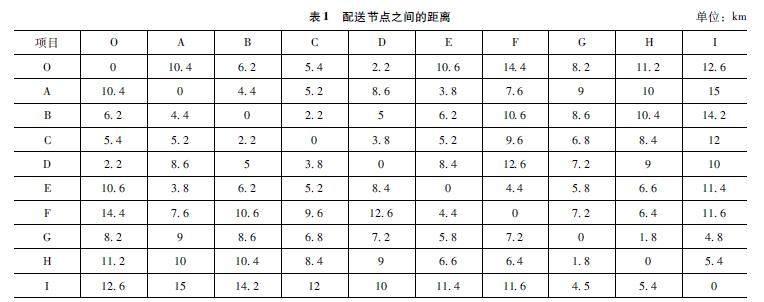
通过对数据进行整理和实际调研,可以假设北京农夫山泉由一辆运力充足的车辆负责配送各个水站所需的货物,在不考虑配送的时间条件下,在其配送过程中寻找最短路径。文章的研究对象是从配送中心出发,然后经过所有配送水站进行补货,最后返回配送中心,其中配送中心到各个水站之间的直线距离如表1所示。
3.2 在Lingo软件中求解TSP模型
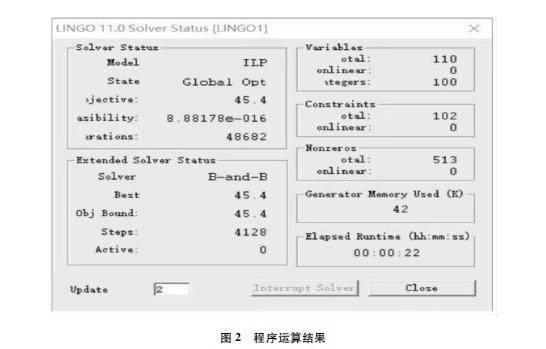
在Lingo软件中TSP模型的编码程序的求解步骤如下所示:第一步,输入相应的变量和系数,然后输入北京农夫山泉配送中心和各个配送水站,每个水站之间的距离、配送中心到各水站的直线距离的数据;第二步,对已有数据进行程序运算;第三步,输出相对应的结果。程序运算结果如图2所示。
在Lingo软件中输入收集的数据,使用Lingo软件运行TSP的程序算法。得到优化后的配送路径,如表2所示。并将运行结果用表格的形式展现出来,由表2可知,0代表不经过该路线,1代表经过该路线。北京农夫山泉配送路径以及总距离如表3所示。
3.3 求解结果分析
根据Lingo软件TSP模型的运算结果分析,优化后的路线为:1-4-3-2-6-7-9-8-10-5-1,将优化后的路线用字母表示为:O-C-B-A-E-F-H-G-I-D-O,最终优化后的配送路径总里程约为45.4km,对比之前所用路线的总里程54.6km,可以明确地看出配送路径总里程减少了9.2km。优化后的路径如图3所示。
4 解决方案
在前文中知道北京农夫山泉的配送路线中存在迂回运输,其原本的配送路线中从配送点H先去到了配送点F然后才到达配送点I,造成了迂回的运输路线。通过运算结果显示,在配送点H处可以先去往配送点G然后再去往配送点I可以减缓迂回路线;在其原本的配送路线中从配送点E开始依次去到了配送点G、H、F、I,这样造成了过远路线。通过运算结果显示,从配送点E开始可以先去到配送点F,然后依次去往配送点H、G、I,以这样的配送路线来配送,可以大大地减少运输总里程,降低运输成本。
对于配送运输不必只局限于对本公司的货物运输,还可以在不影响本公司配送的前提下,寻找可以合作的企业,在本公司的运输路线下对其企业的货物进行运输并收取相应的运费,建立互通有无的合作关系。
同时,也可以在返程的途中购买企业所需的用品。还需要通过自身的数据库,尽己所能地把握货物信息、车辆信息及采购信息,并做到及时与货车司机沟通,将返程空驶的问题解决。
比如在配送站I附近有一家小的商店,他们每次进货需要跑到配送中心O附近的批发市场进行采购,每次采购东西的时候批发市场是不会派车辆给他们进行运输的,需要他们自己去找车辆。
如果可以和北京农夫山泉达成合作,不仅可以减少一部分采购费用,还可以使北京农夫山泉在这个过程中解决返程空驶的问题,同时增加一部分盈利。
5 结论
随着现代物流产业的急速发展,配送路径是否合理一直是物流配送过程中不断研究讨论的问题。文章以北京农夫山泉的配送路径优化为研究目标,通过研究其现有配送路径以及其在配送过程中存在过远运输、迂回运输和返程空驶等问题,从现有配送路径进行分析,建立相对应的数学模型,运用Lingo软件的TSP算法进行求解,得出最優的配送路径,同时也能为其他企业的配送路径优化提供借鉴。总结本篇文章,得出以下结论。
第一,文章利用Lingo软件对北京农夫山泉的配送路径进行分析优化,成功地将其配送路径总里程从54.6km降低到45.4km,总配送路径减少9.2km。设计了新的配送路径,解决了原有配送路径中存在的过远运输和迂回运输问题,能够有效地提升配送运输效率,控制运输配送成本,对企业的实际运营管理有着较大的现实意义。
第二,为了确保司机能够在新规划的路径上进行运输,北京农夫山泉还需加强监管机制,对每次运输的过程进行记录,规范员工们的行为;还应寻找合作企业,可以对其公司的商品在自身路线中进行运输,解决返程空驶的问题。建立自身数据库,更明确地把握车辆的运输情况。
参考文献:
[1]尚猛,万志鹏,曹峻玮,等.基于改进鲸鱼优化算法的物流路径优化[J].数学的实践与认识,2019,49(15):210-218.
[2]郭宝恩.基于Spark的蚁群算法在物流配送路径优化问题中的应用研究[J].信息与电脑(理论版),2018(3):50-52.
[3]田鸽,薛冬娟,梁斌,等.基于改进蚁群算法的冰鲜水产品配送路径优化方法研究[J].大连海洋大学学报,2019,34(5):746-751.
[作者简介]高一丹(2002—),女,山西忻州人,天津科技大学经济与管理学院,研究方向:财务管理;张钰瑶(2002—),女,山西晋城人,上海师范大学化学与材料科学学院,研究方向:应用化学;郑巧(2001—),女,重庆人,西南财经大学国际商学院,研究方向:国际商务(中外合作办学);徐成钰(2003—),女,山东潍坊人,山东科技大学外国语学院,研究方向:英语;通讯作者:赵萌(2004—),女,河北承德人,西南财经大学管理科学与工程学院,研究方向:信息管理与信息系统。

