结构化学热点“晶胞计算”的几何解法
韩建丰 高凌蕊


结构化学部分高考题目考查内容为:①核外电子排布,包括基态(激发态)原子电子排布式(或轨道表示式)、I1(第一电离能)、电负性、元素周期表及周期律等;②分子的结构与性质,共价键理论、杂化轨道理论、VSEPR(价层电子对互斥模型)分子空间构型、极性、分子间作用力等;③晶胞结构与性质,包括常见晶体的堆积方式、配位数、晶胞计算、晶体类型及性质比较等。这三个方面在高考题中呈现出“由易到难、层级递进”特点,晶体结构与性质部分相对而言难度较大。
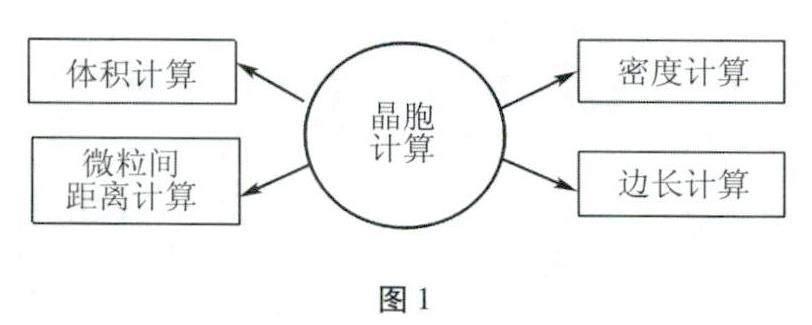
有关晶体的热点考查内容为“晶胞计算”,在各地的化学高考中都属于难点内容。晶胞计算涉及相关内容有:常见晶胞结构特点、晶胞中原子分数坐标、晶胞简单计算(均摊法、晶胞密度、半径),高频考点如图1所示。
可见晶胞空间结构和微粒间的位置关系是晶胞计算的核心,不妨从原子坐标出发建立空间坐标系,使用几何知识解决问题。通过迁移“高中数学知识”可以高效快速解决晶胞计算问题。
一、晶胞计算幾何解法模型应用示例
晶胞计算的关键在于清晰确定各粒子的空间位置,借助空间坐标系确定原子分数坐标即可形成清晰认知,从而形成“晶胞计算”的几何解法模型,如图2所示。
建立模型让晶胞计算的化学问题变为简单数学问题,培养学生跨学科综合素养、通过几何推理和计算解决化学“难点”的能力。探寻“晶胞计算”考查方式和几何解法,可逐步形成模型认知,使学生具备此类问题的解题思路、方法、技巧和信心。学生的几何解法模型建立后应通过理解、记忆、掌握、运用模型认知解题,在运用中夯实基础提升思维水平。
晶胞计算问题作为部分学生化学学习的“难点”,应用“几何计算”可以突破,而用到的数学知识仅为初中水平。
例题1 Cu+和F-形成的晶胞结构如图3所示,其晶胞密度为a(g/cm3),求阴阳离子最近距离(单位pm)。
解析 应用几何解法可将粒子位置清晰可视化。
[几何解法:确定粒子位置]
可建立三维空间坐标系。如图4所示。
晶胞是无隙并置的,在化学中认为8个顶点坐标均为(0,0,0)。但若只从单个品胞的数学角度(按照空间直角坐标系规则)则可设立方体边长为1,在空间坐标系中可确定图4中的8个顶点坐标:(0,0,0)、(1,0,0)、(1,l,0)、(0,1,0)、(0,0,1)、(1,0,1)、(1,1,1)、(0,1,1);

