喷水推进器系泊工况性能的数值模拟
冯若凡,梁天雄,梁宁,曹琳琳,吴大转
(1.浙江大学 化工机械研究所,浙江 杭州 310027;2.浙江省清洁能源与碳中和重点实验室,浙江 嘉兴 314031)
喷水推进作为典型的船舶推进方式,具有低噪声、高效率、机动性好等优点[1-2].在喷水推进器的研制过程中,系泊试验是评估其推进性能的重要手段,可以用于直接测量推力,测试整机的运行稳定性.系泊试验只能测量推进器总推力、主机功耗、扭矩等外特性参数,较难得到各组件的性能数据,如叶轮推力、流道阻力,更不能得到推进器内部流场的细致分布情况[3],因此对于喷水推进器优化设计工作的指导意义较有限.形成一套可精细准确模拟喷水推进器内流特性的数值模拟方法,与系泊试验数据联合,可以有效地辅助喷水推进器内流特性分析与水力模型优化,具有较大的指导意义.
目前业内常用的喷水推进器主流数值模拟方法经常将喷水推进器流场简化为封闭流场,也有部分采用基于船舶-推进器耦合的自由流场计算方法.Eslamdoost 等[4-5]使用体积力模型,模拟泵的内部流场.Bulten 等[6-7]基于泵的叶轮、导叶体和喷口部分,建立封闭单相计算域进行计算.Huang 等[8]基于进口流道部分,建立封闭单相计算域进行计算.靳栓宝等[9-10]模拟喷水推进器在封闭试验管路中的工作情况.Huang 等[11-13]进行单相敞水计算.在喷水推进器的数值计算中,封闭流场的计算方法居多.这种方法对计算资源的需求相对较低,但很难模拟喷口的自由射流,常在喷口处用管路代替射流[14-16].基于前期研究,不同的管路设置会对计算结果产生较大的影响.
Takai 等[17-20]采用基于船舶-推进器耦合的自由流场计算方法,能够模拟喷口自由射流以及船体与推进器之间的相互作用,比较接近真实情况,但对计算资源的需求较高,依赖这种计算方法不利于喷水推进器优化设计的快速迭代.
本文采用基于VOF 模型的可模拟自由液面和喷口射流的数值模拟方法,采用系泊试验结果验证了该方法的可靠性.使用该方法,分析喷水推进器系泊工况下的内流场特性.
1 数值计算与试验方法
1.1 研究对象
以某艉板式喷水推进器为研究对象,基本结构如图1 所示,包含进口流道、叶轮、导叶和喷口.如表1 所示为该推进器的主要设计参数.表中,nr为额定转速,qm为质量流量,Hr为扬程,D为叶轮直径,Cr为叶轮叶片数,Cs为导叶叶片数.

表1 喷水推进器的参数Tab.1 Parameters of waterjet propulsion
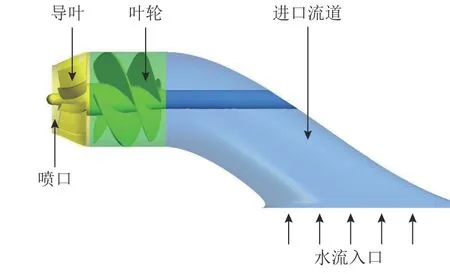
图1 喷水推进器的结构Fig.1 Structure of waterjet propulsion
1.2 系泊试验
为了验证数值模拟方法,自行设计了系泊试验台,如图2、3 所示.试验台的主要结构包括浮箱和外部框架.浮箱内部装有喷水推进器、驱动器、传动机构和扭矩传感器等.浮箱整体浮动仅在侧向有约束,外部框架固定在地面上.外部框架和浮箱通过直线轴承和拉力传感器连接,直线轴承能够将两者的相对运动限制在推力方向,通过拉力传感器直接测量喷水推进器的推力.

图2 喷水推进器系泊试验台的结构Fig.2 Structure of mooring test rig for waterjet propulsion

图3 喷水推进器系泊试验台的搭建Fig.3 Construction of mooring test rig for waterjet propulsion
喷水推进器的导叶体后还装配了转向倒车机构,在倒车斗没有放下,转向喷口朝向正后方时,可以测量喷水推进器正航工况下的性能.通过改变转向喷口的朝向,可以测量喷水推进器转向工况下的性能.通过将倒车斗放下,可以测量喷水推进器倒车工况下的性能.这些数据可以为喷水推进器的性能评估提供参考,为数值计算的结果提供试验验证.
1.3 基于VOF 模型的数值模拟方法
采用基于有限体积法的软件FLUENT 2021R1,基于雷诺时均纳维-斯托克斯(Reynolds average Navier-Stokes,RANS)方程,对喷水推进器内外流场进行三维、定常、不可压缩的数值求解.湍流模型采用切应力模型(shear stress transport,SST).该模型在近壁面区域采用k-ω 模型,在远离壁面区域采用k-ε 模型,弥补了标准k-ω 模型对边界条件过于敏感的缺点.多相流模型采用VOF 模型,它的基本原理是利用计算网格单元中流体体积量的变化和网格单元本身体积的比值函数F 来确定自由面的位置和形状,对自由液面进行捕捉[21].求解器使用基于压力的耦合算法,有利于改善收敛性.采用多重参考系方法(multiple reference frame,MRF)模拟叶轮的旋转运动,将叶轮区域设置为旋转坐标系,其他流场区域为固定坐标系,两者通过设置交界面来实现数据的传递.
计算域包含浮箱及其周围流场,如图4 所示.将喷水推进器的部件和浮箱的表面都设置为无滑移壁面,将入口设置为压力入口,出口设置为压力出口.设置明渠流动,在压力入口处定义液面高度,使自由液面在计算开始时浸没喷水推进器喷口的一半.
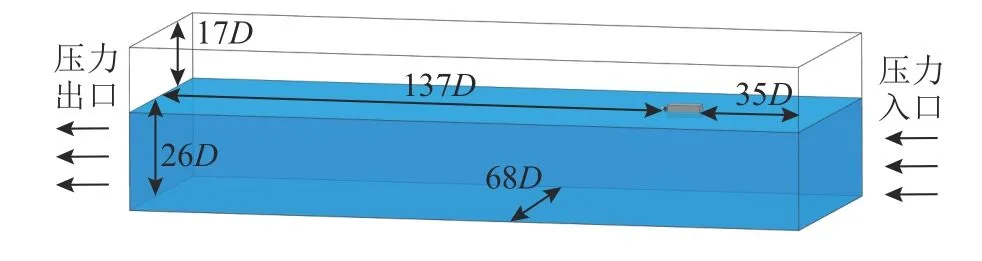
图4 数值模拟计算域和边界条件Fig.4 Computational domains and boundary conditions of numerical simulation
将计算域划分为进口流道、叶轮、导叶、喷口附近外流场和远离喷口外流场5 个区域.其中叶轮和导叶区域采用Turbogrid 软件划分结构化网格,进口流道和喷口附近外流场区域采用ICEM CFD 软件划分非结构化网格,远离喷口的外流场采用ICEM CFD 划分结构化网格,在自由液面附近进行加密.在喷水推进器的流道和叶轮、导叶等过流部件表面采用边界层网格,进口流道边界层的第1 层高度为0.2 mm,增长率为1.2,共5 层.进口流道和导叶的表面 y+为20~40,叶轮的表面y+为30~150,可以满足壁面函数法的求解要求.计算域各部分的网格单元数见表2.如图5 所示为各部分网格示意图.

表2 计算域各部分的网格单元数Tab.2 Number of grid cells in each part of computational domains
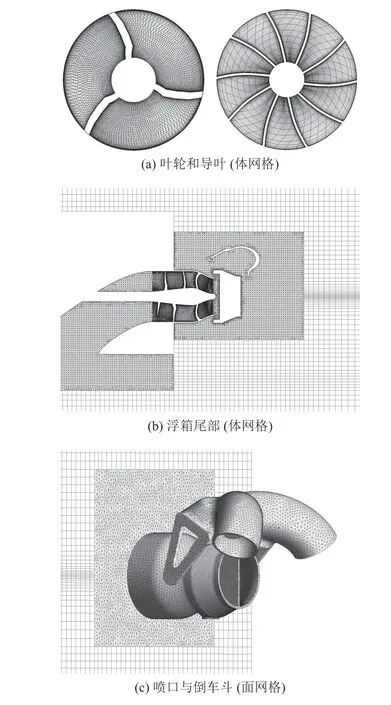
图5 计算域各部分的网格Fig.5 Grids of various parts of computational domains
通过更改网格尺寸,形成由疏到密的4 套网格,网格细化比为1.2,网格数见表3.表中,N 为总网格数.选取叶轮转速为887 r/min 的正航工况,开展网格无关性分析.选取扬程和转矩作为目标量,含义如下所示:

表3 不同密度的4 套网格的数量Tab.3 Number of four sets of grids with different densities
式中:Q为转矩,P为泵的轴功率,ω为泵的转动角速度.
结果如图6 所示.可以看出,当网格数达到9 550 521 时,相较于网格数为11 507 092 时的计算结果,转矩相对误差为0.05%,转矩基本保持不变.为了进一步验证收敛性,选取转矩作为目标量进行验证和确认,将试验不确定度假定为6%,结果如表4 所示.表中,RG为收敛率,USN为数值不确定度,UV为确认不确定度.收敛率满足 -1.0 <RG<0,属于振荡收敛,且不确定度较低,说明网格已收敛,数值计算的结果具有一定的可信度.综合考虑计算的精度和经济性,选择网格单元数为9 550 521 的2 号网格进行后续计算.

图6 网格无关性分析Fig.6 Grid independence analysis

表4 转矩不确定度的分析结果Tab.4 Results of uncertainty analysis of torque
2 计算结果分析
2.1 外特性参数和喷射流场分析
正航状态与倒航状态下的数值计算与试验结果的对比如图7 所示.图中,n为泵转速,KT为推力系数,KQ为转矩系数,其定义为

图7 喷泵性能参数的计算结果与试验结果对比Fig.7 Comparison between calculated and experimental results of waterjet pump performance parameters
式中:T为推进器总推力或倒车力,Q为泵转矩,D为泵叶轮直径.
从图7 可以看出,在正航时,利用数值计算得到的系泊推力较试验结果偏大,在大多数工况下相对误差约为5%;利用数值计算得到的转矩较试验结果偏小,在大多数工况下相对误差为5%~10%.在倒航时,利用数值计算得到的倒车力较试验结果偏大,在大多数工况下相对误差约为10%;利用数值计算得到的转矩较试验结果偏小,在大多数工况下相对误差小于5%.
利用数值计算得到的推力普遍大于试验结果,这可能是由于试验测量装置不能准确测量所有推力,一部分推力在试验装置的部件中被消耗,导致测量值小于实际推力.在倒航时,由于倒车斗对喷口流场的影响,推力的消耗进一步增加,数值计算的稳定性有所降低,导致倒车力的计算相对误差比正航时更大.利用数值计算得到的转矩结果普遍小于试验结果,这可能是因为数值计算只能得到理论转矩,而在试验中,力矩在机械部件之间传递时会发生损失,导致实际转矩大于理论值.在泵转速较低的情况下,由于数据的绝对值很小,计算值与试验值的绝对误差相比于高转速时减少不多,导致相对误差较大.
如图8 所示为在正航工况下,叶轮转速分别为1 485、887 和293 r/min 时的喷射流场.可以看出,射流在刚离开喷口时速度最大,液面高度最大,离开喷口的距离越远,在阻力作用下速度越小,在重力作用下液面高度越小,逐渐过渡到自由液面.
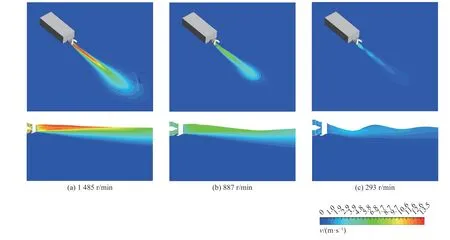
图8 不同转速正航工况下的喷射流场Fig.8 Jet flow field at different pump speeds under forward conditions
喷口射流长度与泵扬程、泵扬程与泵转速的二次方之间的关系如图9、10 所示.图中,射流长度 L定义为射流液面高度首次下降到与自由液面同一水平的位置到喷口的距离,扬程的定义如下所示:

图9 射流长度与扬程的关系Fig.9 Relationship between jet length and head
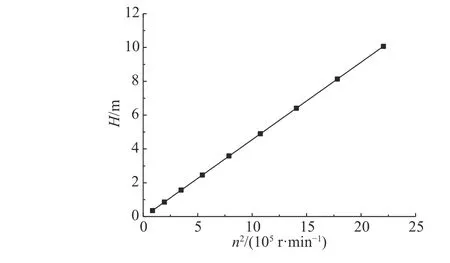
图10 扬程与叶轮转速的关系Fig.10 Relationship between head and pump speed
式中:p0、pi分别为喷泵出口、入口处的静压力,v0、vi分别为喷泵出口、入口处的流速,z0、zi分别为泵出口、入口相对于某一点的高度差.
由图7 可知,射流长度与泵扬程近似成正比,泵扬程与转速的二次方成正比,即
泵的有效功率可用下式表示:
式中:qV为泵的体积流量.
泵做功能力的强弱可以通过射流形态表现出来.射流的长度越大,泵的转速越大,扬程越高,做功能力越强.
利用数值计算能够得到喷水推进器在系泊工况下的喷射流场,推力和转矩参数与试验数据在大多数工况下较接近.可以认为,该数值计算方法是可信的.
2.2 喷水推进器内部流场的分析
基于以上数值计算方法,从欧拉扬程分布和单位体积熵生成率2 个方面,研究喷水推进器系泊工况下的内流特性.
2.2.1 总体欧拉扬程分布 喷水推进器内部流体的能量来源是叶轮做功,叶轮的能量增长方式在很大程度上影响喷水推进器的水力性能.总体欧拉扬程分布可以表征从叶轮前缘到尾缘总体能量增长过程的特征分布[22],通过研究它可以了解叶轮的总体能量增长情况,分析喷水推进器的水力性能.
根据欧拉扬程的定义可知,欧拉扬程与液体在叶轮中的绝对速度圆周分量和圆周速度成正比,
式中:vu为绝对速度圆周分量,u为圆周速度,g为重力加速度.
叶轮的前缘面和尾缘面如图11 所示.在叶轮的前缘和尾缘间选取若干叶轮周向面,计算欧拉扬程在不同的叶轮周向面上的面平均值,可得叶轮的总体欧拉扬程分布.

图11 叶轮的前缘面和尾缘面Fig.11 Leading and trailing edge surfaces of impeller
如图12 所示为正航工况下叶轮处于不同转速的总体欧拉扬程分布情况.图中,BS为叶轮轴向位置,HE为总体欧拉扬程.大约在 BS=0.2处,总体欧拉扬程曲线逐渐分散并按照一定的斜率上升,大约在 BS=0.8处曲线趋于平缓,转速越高,最终欧拉扬程的稳定值越高.可以看出,欧拉扬程与叶轮转速呈正相关,当转速不同时,总体欧拉扬程的增长规律相似.

图12 不同流量下叶轮的总体欧拉扬程分布Fig.12 Overall Euler’s head distribution of impeller under different flow rates
如图13 所示为正航工况下叶轮处于不同转速的正则化总体欧拉扬程分布情况.图中,En为正则化总体欧拉扬程,它的含义是设叶轮从前缘到尾缘的总能量变化为1,将曲线转变为能量从0 到1.0 的变化过程,可以表征能量在叶轮中的增长方式.从图13 可以看出,正则化总体欧拉扬程所有的曲线遵循先加速上升、后减速上升的规律.

图13 不同流量下的叶轮正则化总体欧拉扬程分布Fig.13 Normalized overall Euler’s head distribution of impeller under different flow rates
图13 中,不同转速下的各条曲线较接近,为了更加清晰、直观地显示各转速下正则化欧拉扬程分布的差异,将图13 中各曲线的斜率k 进行统计,得到的结果如图14 所示.从图14 可以看出,每条曲线的斜率变动范围是接近的,且在BS=0.45 处相交.当转速降低时,靠近叶轮入口处的曲线斜率增大,靠近叶轮出口处的曲线斜率减小.此时曲线的整体斜率变化增加,曲线的上凹幅度更大.

图14 正则化总体欧拉扬程曲线的斜率分布Fig.14 Slope distribution of normalized overall Euler’s head curve
如图15 所示为泵叶轮效率与泵转速之间的关系.图中,ηb为叶轮效率,

图15 叶轮效率随转速的变化Fig.15 Variation of impeller efficiency with pump speed
式中:Hb为叶轮扬程,qV为体积流量.
从图15 可以看出,随着转速的升高,叶轮的效率逐渐提高.对比分析图13~15 可知,正则化总体欧拉扬程曲线的分布方式与叶轮效率存在关联,曲线的形状越接近一条直线,曲线的增长率越趋于恒定,效率越高.在严鹏[22]对混流泵内部流动特性的研究中发现了相似的规律.
2.2.2 基于单位体积熵生成率的流动损失分析 喷泵的效率可以用下式进行表示:
计算得到的效率与转速的关系如图16 所示.在低转速时泵的效率较低,随着转速的升高,泵的效率升高,并逐渐趋于稳定.泵的效率与泵内部的流动损失密切相关.

图16 泵效率与转速的关系Fig.16 Relationship between efficiency and pump speed
熵增是适用于衡量绝热机器内损失大小的物理量.为了对喷泵内部的主要损失区域进行定位,采用单位体积熵生成率对喷泵内部的流动损失情况进行分析.根据熵增的原始公式可知,熵增可以分为由热通量引起的熵增变化和由流体的黏性效应引起的机械能耗散2 部分.在喷水推进器的数值模拟中,可以认为泵的温度场不变,所以由热通量引起的熵增变化可以忽略[23-26].只须计算流体的黏性耗散与湍流耗散引起的熵增:
为了研究叶轮内部的熵增情况,取span=0.5 的展向平面,绘制叶轮的展开图,可以看到叶轮内部的熵增区域分布情况,如图17 所示.

图17 叶轮区域的熵生成率Fig.17 Entropy generation rate of impeller region
从图17 可以看出,总体熵增与转速呈正相关,熵增区域主要集中在叶片附近,这表明叶轮的损失主要来源于叶片壁面的摩擦及叶轮的尾迹.为了定量比较叶轮各个不同区域的流动损失情况,将叶轮划分为近轮毂区(span=0~0.1)、轮毂侧主流道区(span=0.1~0.5)、轮缘侧主流道区(span=0.5~0.9)、近轮缘区(span=0.9~1.0),计算每个区域的熵生成率,结果如图18 所示.图中,PEn为熵生成率占比.

图18 不同区域的熵生成率占比Fig.18 Percentage of entropy generation rate in different regions
从图18 可以发现,随着叶轮转速变化,叶轮内各区域熵生成率的占比基本相同,总熵增会随着转速的增加而增大.当转速为1 485 r/min 时,叶轮内部产生的熵增现象最明显.为了更好地分析熵增形成的原因,选择转速为1 485 r/min 的工况,对泵叶轮流场进行进一步的分析.该转速下不同截面处叶栅间的单位体积熵生成率分布如图19所示.从图18、19 可知,近轮毂区和主流道区的熵生成率较小,近轮缘区的熵生成率较大,占总熵生成率的44.5%,主要由叶顶泄漏导致.
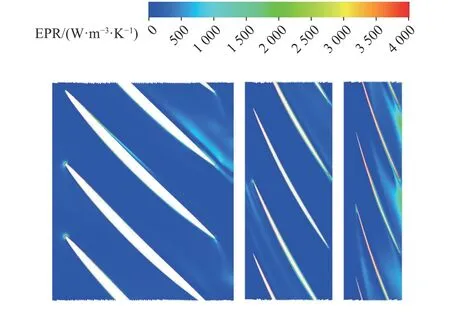
图19 转速为1 485 r/min 时的叶轮单位体积熵生成率(span=0.05、0.50、0.95)Fig.19 Entropy generation rate of impeller region at speed of 1 485 r/min (span=0.05、0.50、0.95)
如图20 所示为叶轮展向熵增分布云图.图中,vf为流速.可以看出,叶轮内部靠近前缘的一侧为熵增集中带,这部分流动损失的形成可能与相邻的进口流道有关.
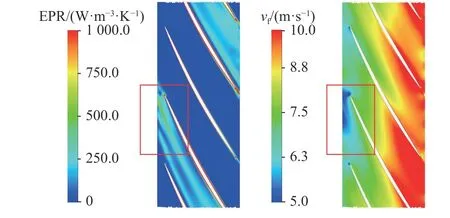
图20 叶轮的熵生成率增及速度分布(span=0.5)Fig.20 Entropy generation rate and velocity distribution of impeller(span=0.5)
如图21、22 所示分别为叶轮前进口流道的熵增和速度分布图,可以观察到进口流道的下方内壁面发生了流动分离现象,引发了涡流和熵增.图23 中使用Ω 涡识别方法得到的涡分布图印证了这一点[27].如图24 所示为叶轮前的轴向截面速度分布,z 越小表示该平面距离叶轮入口越远.从图24 可知,在叶轮下方存在低速区域,在与叶轮接近的过程中,该区域的速度分布受到叶轮的诱导影响,形状逐渐与叶轮的前缘相似.2 个叶片之间熵增带的形成原因是进口流道发生流动分离现象而形成的涡流.该涡流传递到叶轮入口处,并受到叶轮的挤压作用,在涡流和叶轮的双重作用下,部分涡流的流动更加紊乱,产生了更大的流动损失.

图21 进口流道的熵生成率分布(1 485 r/min)Fig.21 Entropy generation rate distribution of waterjet duct (1 485 r/min)

图22 进口流道的流速分布(1 485 r/min)Fig.22 Velocity distribution of waterjet duct (1 485 r/min)

图23 进口流道的涡分布Fig.23 Vortex distribution of waterjet duct

图24 叶轮进口前各截面的流速分布情况(1485 r/min)Fig.24 Velocity distribution at each section before impeller inlet(1 485 r/min)
如图25 所示为进口流道附近的流向矢量分布图.可以看出,液体从流道进口的前方、下方、后方进入流道,其中从前方进入流道的液体能够与进口流道的内壁面形状相匹配,但从下方甚至后方进入进口流道的液体不能很好地顺着内壁面进入流道,会在下方内壁面发生流动分离的现象,产生涡流与熵增.造成这种情况的主要原因可能是系泊工况与喷水推进器的常规运行工况不同.喷水推进器在常规情况下运行时,船舶具有一定的航速,外流场的液体相对于推进器从泵的进口向出口方向运动,主要是进口流道前方的来流顺着流道进入喷水推进器,从流道入口下方和后方进入流道的液体较少.在系泊工况下,外流场的液体相对于推进器内流场速度较低,内、外流场的速度差较大,流道入口下方甚至后方的大量液体被吸入流道,在内壁面的转角处极易发生流动分离,导致大量损失.

图25 进口流道的速度矢量图Fig.25 Velocity vector diagram of waterjet duct
进口流道处发生流动分离导致的涡流与熵增以及之后传递到叶轮区域的熵增带,与系泊试验工况自身条件存在较大的关联.
3 结 论
(1)利用数值计算得到的推进器总推力、转矩与系泊试验结果较吻合.计算得到的喷口射流长度与泵的扬程近似成正比,与泵的转速的二次方近似成正比,与有效功率的三分之二次方近似成正比.
(2)基于VOF 模型、包含自由液面和喷口射流的数值模拟方法,使用总体欧拉扬程分布、单位体积熵生成率的方法对喷水推进器的内部流场进行分析.可以发现,欧拉扬程曲线的增长率与叶轮的效率密切相关,在系泊试验且不考虑空化的工况下,叶轮的转速越高,叶轮欧拉扬程曲线的增长率越趋于恒定,叶轮效率越高.叶轮内部的流动损失主要由壁面摩擦、叶轮尾迹和叶顶泄漏等导致,在系泊工况下进口流道处易发生流动分离,造成局部流动损失.
(3)相较于简化的封闭流场计算方法,利用本文所使用的数值计算方法能够模拟自由液面和喷口射流,可以得到更准确的喷水推进器性能数据与内外流场分布.相较于基于船舶-推进器耦合的自由流场计算方法,本文所使用的数值计算方法对计算资源的需求更低.通过这种基于VOF 模型、包含自由液面和喷口射流的数值模拟方法,与系泊试验数据联合,可以有效地辅助喷水推进器的内流特性分析,为喷水推进器的优化设计提供参考.

