管卡位置对海管立管的敏感性分析

崔建国, 董志滟, 崔永涛, 李民强

(1.胜利油田分公司海洋采油厂, 山东 东营 257237; 2.中石化胜利石油工程有限公司钻井工艺研究院, 山东 东营 257000)

海管立管作为海面与海底的联系通道,更是海洋油气开采系统的重要部件之一。海管立管与其他海洋结构物相比,所处的海洋环境更加复杂恶劣,管道部受到高温高压的石油或天然气等流动介质的腐烛,外部还要受到海风、海浪、海流、海冰和地震等自然环境的影响。在这种复杂多变的恶劣环境下,海管立管很容易遭到破坏,从而导致各种难以想象的事故发生,如油气泄漏、火灾,甚至爆炸等,造成人员伤亡、经济损失和环境污染,甚至破坏整个海洋环境生态系统,后果极其严重[1-4]。

随着数值模拟技术的快速发展,有限元模拟技术越来越广泛应用到工程领域,数值模拟技术与试验研究手段相辅相成,相互补充与验证。因此,有必要提出一个可以模拟复杂荷载作用下立管触地段损伤管道力学性能的数值模型,进而开展深入的研究,以掌握复杂荷载作用下立管的疲劳分析[5-7]。

国内外学者对油气管道的安全评价进行了大量研究,油气管道安全评价相关的理论和技术也日趋成熟。我国关于海洋工程及海管立管方面的安全评价研究工作起步较晚,目前还没有形成一个科学的、统一的、权威的用于评价海洋工程及海管立管安全级别的评价指标体系,也无专门的、系统的和完善的在役立管触地段海底管道安全评价方法。现有的研究成果无法为海管立管提出一个科学有效的安全评价模型,海洋工程方面的安全评价还未能达到工程实际的相关要求[7-9]。

管卡是海管立管与平台固定的必要设备,该设备会对海管立管的结构产生直接的影响,其安装位置影响到海管立管的受力,产生的应力会影响海管立管的使用寿命,因此,要对管卡对海管立管的结构进行敏感性分析,根据其影响效果,优化管卡的安装位置,延长海管立管的使用寿命[10]。

1 海管立管力学模型建立

1.1 有限元模型的建立与准确性验证

1.1.1 模型前处理

针对海管立管建立有限元模型,通过理论计算推导结果与ABAQUS有限元分析软件分别对模型进行准确性验证。根据海底注水管道参数条件,由于破坏的为立管外管,因此为简化计算,只针对立管外管展开分析。

海管立管的基本参数为外管φ377×13,外管为φ273×13,材质均为16Mn。海管立管水上0.5 m、水上4 m、水下2 m、水下6 m处设置管卡,水平段 6、13、30 m设有水下桩,36 m处入泥。作业水深15 m,施加水平波浪载荷,设计波高6.0 m,周期8.1 s;海面流速1.02 m/s,中部流速0.91 m/s,海底流速0.87 m/s,内管流体压力为4 MPa,水面以上立管结构施加风载,设计风速为30.8 m/s。

基于以上参数及海况建立的海管立管有限元模型如图1所示,管道变形较大,且端盖对管道具有整圆作用,受力较大,整体采用实体单元建模,对弯管处进行网格细化,节点数为105 236个,单元数为18 853个。有限元模型载荷及边界条件的施加情况如图2所示,管卡及水下桩位置设置全约束,平台井口位置立管外管与悬挂器之间设置耦合点,建立双层管与平台间的耦合关系。对外管与管卡位置建立耦合约束,将桩腿与管卡建立为一个模型,将管卡内表面与外管外表面接触位置建立分布耦合,将两表面耦合于一点,即此区域各节点与参考点之间建立了一种约束关系,对此区域上各节点的运动进行加权平均处理,使此区域上受到的合力和合力矩与参考点上的力和力矩等效。水下桩耦合形式与管卡相同。外管与内管连接处,对内外管之间建立耦合关系,将内外管连接处同时耦合与一点,即将内外管连接处建立刚性连接,此区域变为一个刚性体,内外连接位置之间的相对位置在分析过程中保持不变。

RP-0至RP-4为外管与管卡位置的5个耦合点

水平段入泥后设置为弹性地基梁约束,用弹性边界来反映管道和土体之间的相互作用。分别考虑不同弹性刚度系数和管道悬空、悬跨情况,探究地基梁约束规律、不同海床淤泥弹性系数对海管应力大小及位置影响规律。在立管分析时,参考文献[11],定弹性系数为软淤泥系数2×107N/m3。立管所受波浪载荷及海面流速通过Python语句进行施加[12],加载语句如图3所示。

图3 施加波浪载荷语句

1.1.2 有限元分析结果

基于以上描述对海管施加约束及载荷,进行网格划分后,提交ABAQUS进行计算,得静力计算结果,最大Mises应力为128.6 MPa,最大应力位置在最下方管卡位置,应力云图如图4所示。

1.1.3 理论计算与有限元模型对比验证

基于海管立管理论分析模型,针对直管段开展对比分析,由材料力学圆管应力计算公式得立管受到最大弯曲应力[13]。立管模型应力分析结果见表1。圆管应力σ的计算公式为

(1)

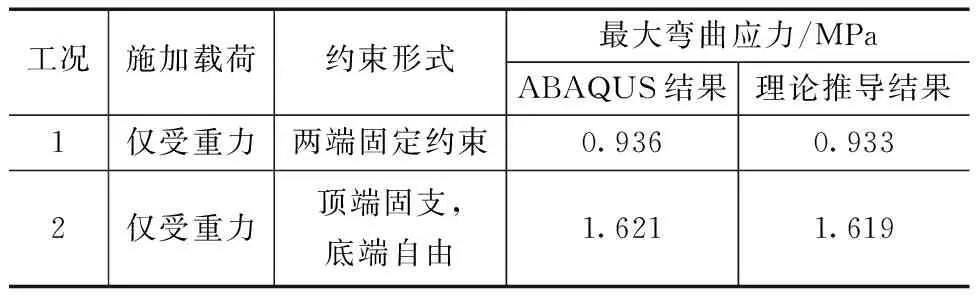
表1 立管模型应力分析结果

式中:σ为弯曲应力;M为弯矩;W为截面模量;FK为正应力;L为力矩;D为立管外径;d为立管内径。

结果显示立管直管段模型在两种工况下,通过施加重力载荷作用以及立管两端设置固定或自由约束形式,通过ABAQUS有限元模拟以及理论推导两种结果对比,最大弯曲应力误差均小于5%,故满足有限元建模准确性要求。

1.2 等效立管模型与双层管计算结果对比

目标海管立管为双层保温结构,内管为φ273×13无缝钢管,外管φ377×13无缝钢管,材质均为16Mn。为减少软件计算量,基于式(2),对双层管道进行合理简化。由于是双层管结构,对此结构进行相当截面的换算,换算依据等效前后的以下关系[14]。

(2)

式中:Ws1为双层管结构的水下重;Ws2为双层管结构等效截面的水下重;D1为双层管结构外管的外径;D2为双层管结构等效截面的外径。

通过以上关系求出壁厚,并且对等效的截面属性进行修正,最终输入的等效管道模型为: 外径377 mm,壁厚21.76 mm,材质为16Mn。

同样对等效后的海管立管进行以下约束:海管立管水上0.5 m、水上4 m、水下2 m、水下6 m处设置管卡,水平段 6、13、30 m设有水下桩,36 m处入泥。作业水深15 m,施加水平波浪载荷,设计波高6.0 m,周期8.1 s;海面流速1.02 m/s,中部流速0.91 m/s,海底流速0.87 m/s,内管流体压力为4 MPa,水面以上立管结构施加风载,设计风速为30.8 m/s。

基于以上描述对海管立管施加约束及载荷,进行网格划分后,提交ABAQUS进行计算,得静力计算结果,最大Mises应力为133.6 MPa,最大应力位置在最下方管卡位置,应力云图如图5所示。

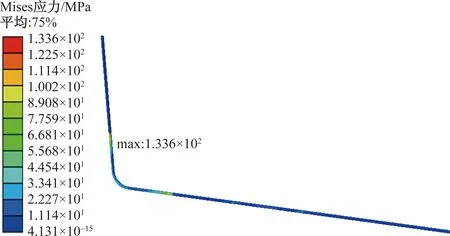
图5 等效立管计算应力云图

根据现场检测应力结果,海管立管关键点应力强度约为120 MPa。基于双层管的有限元结算结果,最大Mises应力为128.6 MPa,最大应力位置在最下方管卡位置。基于等效立管的有限元结算结果,最大Mises应力为133.6 MPa。将计算结果进行对比,不难发现,双层管计算结果更加准确,更贴合实际,故后续海管立管的计算建议采用双层管进行。

2 管卡位置对立管结构敏感性分析

2.1 管卡位置对立管强度的影响

对管卡位置对立管的影响进行研究,主要分7个工况,水平段在6、13、30 m处设有水下桩,立管在36 m处入泥。作业水深15 m,施加水平波浪载荷,设计波高6.0 m,周期8.1 s,海面流速1.02 m/s,中部流速0.91 m/s,海底流速0.87 m/s,内管流体压力为4 MPa。除管卡位置外,其余加载保持不变。

管卡位置约束:①1、2、3号管卡位置不变,4号管卡分别放置在水下4 m、水下6 m、水下8 m、水下10 m处,分析最下方管卡位置对立管的影响;②2、3、4号管卡位置不变,1号管卡分别放置在水上4 m、水上3 m处,分析最上方管卡位置对立管的影响;③1、3、4号管卡位置不变,2号管卡分别放置在水上0.5 m、水上2 m处,分析2号管卡位置对立管的影响;④1、2、4号管卡位置不变,3号管卡分别放置在水下2 m、水下4 m处,分析3号管卡位置对立管的影响。

将模型导入ABAQUS有限元分析软件,按实际工况对模型进行加载,分析结果见表2。应力位移云图如图6～图12所示。

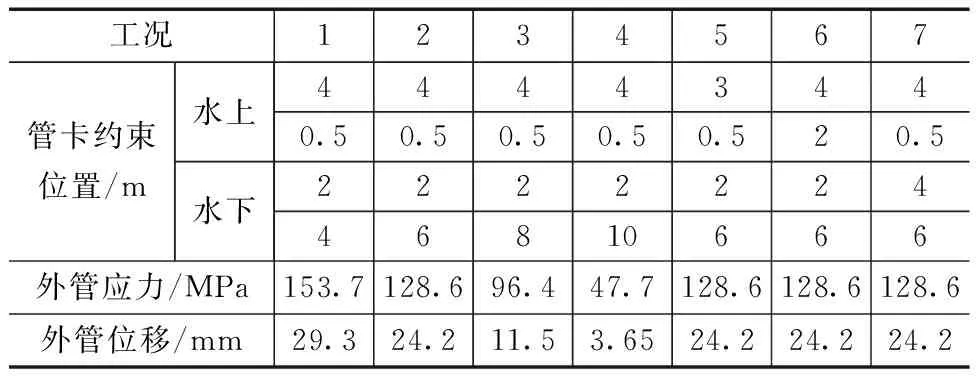
表2 管卡位置对立管强度影响计算结果

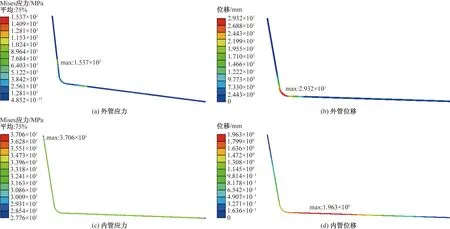
图6 工况1外管应力、外管位移、内管应力、内管位移云图

对立管模型按表2中工况1固定管卡位置,得外管应力云图如图6(a)所示,最大应力为153.7 MPa,发生在外管最下方管卡位置,外管位移云图如图6(b)所示,最大位移发生在外管弯头处,最大位移为29.3 mm,沿海流流向方向,内管应力云图如图6(c)所示,最大应力为37.06 MPa,发生在外管与内管连接位置,内管位移云图如图6(d)所示,最大位移发生在水平段靠近弯头一侧,最大位移为1.96 mm,位移较小。

对立管模型按表2中工况2固定管卡位置,得外管应力云图如图7(a)所示,最大应力为128.6 MPa,发生在外管最下方管卡位置。外管位移云图如图7(b)所示,最大位移发生在外管弯头处,最大位移为24.2 mm,沿海流流向方向。工况2下内管应力、位移分析结果与工况1相同。

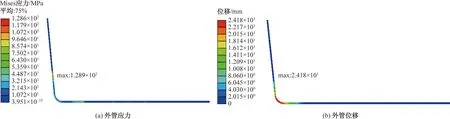
图7 工况2外管应力、外管位移云图

对立管模型按表2中工况3固定管卡位置,得外管应力云图如图8(a)所示,最大应力为96.41 MPa,发生在外管最下方管卡位置,外管位移云图如图8(b)所示,最大位移发生在外管弯头处,最大位移为11.5 mm,沿海流流向方向。工况3下内管应力、位移分析结果与工况1相同。

图8 工况3外管应力、外管位移云图

对立管模型按表2中工况4固定管卡位置,得外管应力云图如图9(a)所示,最大应力为47.7 MPa,发生在外管最下方管卡位置,外管位移云图如图9(b)所示,最大位移发生在外管弯头处,最大位移为3.65 mm,沿海流流向方向。工况4下内管应力、位移分析结果与工况1相同。

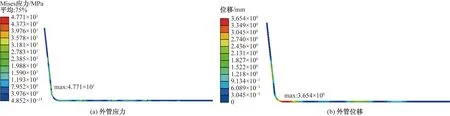
图9 工况4外管应力、外管位移云图

对立管模型按表2中工况5固定管卡位置,得外管应力云图如图10(a)所示,最大应力为128.6 MPa,发生在外管最下方管卡位置,外管位移云图如图10(b)所示,最大位移发生在外管弯头处,最大位移为24.2 mm,沿海流流向方向。最大应力及最大位移结果与工况2相同,但工况5下1、2号管卡位置段应力与工况2应力结果有较小差别,工况5下应力结果偏小约5.6 MPa。工况5下内管应力、位移分析结果与工况1相同。

图10 工况5外管应力、外管位移云图

对立管模型按表2中工况6固定管卡位置,得外管应力云图如图11(a)所示,最大应力为128.6 MPa,发生在外管最下方管卡位置,外管位移云图如图11(b)所示,最大位移发生在外管弯头处,最大位移为24.2 mm,沿海流流向方向。最大应力及最大位移结果与工况2相同,但工况6下1、2、3号管卡位置段应力与工况2应力结果有较小差别,工况6下1、2管卡位置段应力结果偏小约7.3 MPa,2、3管卡位置段应力结果偏大约6.8 MPa。工况6下内管应力、位移分析结果与工况1相同。

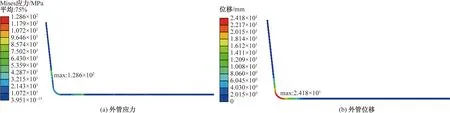
图11 工况6外管应力、外管位移云图

对立管模型按表2中工况7固定管卡位置,得外管应力云图如图12(a)所示,最大应力为128.6 MPa,发生在外管最下方管卡位置,外管位移云图如图12(b)所示,最大位移发生在外管弯头处,最大位移为24.2 mm,沿海流流向方向。最大应力及最大位移结果与工况2相同,但工况7下1、2、3号管卡位置段应力与工况2应力结果有较小差别,工况7下2、3管卡位置段应力结果偏大约7.8 MPa,3、4管卡位置段应力结果偏小约8.3 MPa。工况7下内管应力、位移分析结果与工况1相同。

图12 工况7外管应力、外管位移云图

2.2 管卡位置对立管寿命的影响

将上述强度计算结果导入Fe-safe,设置好材料、算法等相关数据之后,对立管进行疲劳寿命分析,Fe-safe 运行好之后将得到的新的odb文件导入 ABAQUS进行查看。

根据 Fe-safe的计算结果可知,在工况1下,外管在荷载循环次数达到约 133.6万次时于4号管卡下方发生疲劳破坏,在工况2、5、6、7下,外管在荷载循环次数均为达到约 165.6万次时于4号管卡下方发生疲劳破坏,工况3下,外管在荷载循环次数均为达到约266.7万次时于4号管卡下方发生疲劳破坏,工况4下,外管在荷载循环次数均为达到约328.8万次时于四号管卡下方发生疲劳破坏。各工况下内管结构疲劳破坏需至少1 000万次的荷载循环才会发生,可认为内管也不发生疲劳破坏。各工况下内管的疲劳寿命结果均与工况1下内管疲劳寿命结果相同,疲劳寿命云图如图13所示,疲劳寿命以10n计量。由计算结果可以看出,立管各工况下的疲劳寿命最小处和静力学分析的应力最大处为同一位置。分析结果见表3。

表3 管卡位置对立管寿命影响计算结果

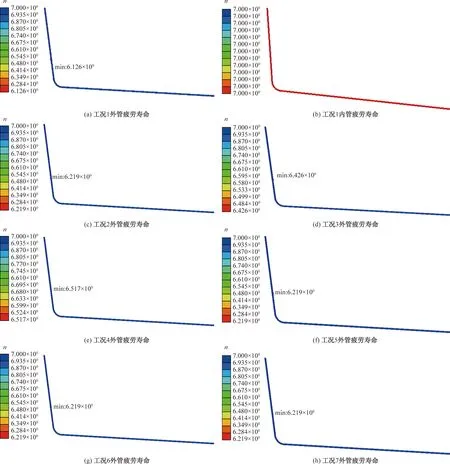
图13 工况1内管疲劳寿命分布云图及各工况外管疲劳寿命分布云图

3 结论

通过以上计算可以看出,波高、流速、水下桩位置、内管压力不变时,不考虑其他因素,仅分析管卡位置对立管结构的敏感性,结论如下。

(1)7个工况下最大应力产生位置均位于4号管卡下方。在管卡约束防护方面得立管安全主要针对最下端管卡,最下端管卡定期移动位置,避免长期应力集中,导致立管失效。

(2)最下方管卡位置(4号)对立管结构强度影响较大,管卡位置越靠下,立管强度性能越好,最下方管卡越靠近弯头,外管使用寿命越长。

(3)1、2、3号管卡位置对立管上部结构强度影响较小,最大应力波动范围在10 MPa以内,对外管使用寿命没有影响。

(4)外管管卡位置对内管应力没有影响,7种工况下内管最大应力均为37.06 MPa,内管寿命均为高周无限。