基于组合赋权-云模型的毕达哥拉斯模糊语言综合评价方法研究

叶梦依, 陈岚辉, 何望琳, 王琦峰

(浙江万里学院物流与电子商务学院, 浙江 宁波 315100)

评价方法和评价模型已广泛应用于决策分析、系统管理和系统工程等诸多领域。汪培庄提出的综合评价是一个重要的数学模型[1]。此后,它被广泛应用于环境评价、教学评价、风险管理、研究项目、汽车检索系统等多个领域。然而,综合评价的一个主要问题是如何兼顾系统随机性和模糊性。对此,李德毅等[2]提出了一种新型不确定性推理理论——云模型。该理论主要利用特征期望(Ex)、熵(En)和超熵(He)来定量表述一个不确定概念,通过云模型实现定性概念与定量数值之间的转换。具体数值打分与评价者的实际感受密切相关,可能导致评价结果具有很大的随机性。云模型的应用能够有效改善这种随机性和映射关系,因为它考虑了评价对象的模糊性、随机性以及不确定性[3],这为综合评价提供了更为灵活和准确的工具。同时为了避免综合评价模型的低效率这一问题,越来越多的研究者将主客观组合赋权法应用于云模型和综合评价中,以更全面地考虑各种因素。王石等[4]通过云理论计算了不同风险等级的各指标云模型参数,并在此基础上利用改进的标准间相关性的重要性-序关系分析(criteria importance though intercrieria correlation-order relation analysis,CRITIC-G1)法对矿山风险进行了评估。何乐平等[5]结合标准化过程和G1-CRITIC,运用博弈论思想优化主客观权重,并提出了一种新的云模型综合风险评价方法。Zhang等[6]提出了一种基于改进综合权重云理论的风险评估方法,采用改进的序关系分析(order relation analysis,G1)法和标准间相关性的重要性(criteria importance though intercrieria correlation,CRITIC)法获取主客观权重,同时运用理想点法得到综合权重。李洁等[7]提出了一种基于组合赋权-云模型的路网韧性评价方法,并制定了提升高速公路网交通韧性的策略。

然而在数据选取方面,仍然存在一些参数难以准确表示的问题。为了解决这一问题,徐青等[8]在毕达哥拉斯模糊环境下,引入云模型进行在线课程评估优选,提出了一种基于毕达哥拉斯模糊云的在线课程用户体验评价方法。本文为了克服了单一权重可能导致的信息损失,在权重确定方面,采用了G1主观权重和CRITIC客观权重,并基于博弈论进行组合。又将毕达哥拉斯模糊数引入决策环境和云模型中,提出一种将毕达哥拉斯模糊数与云模型相结合的组合赋权的综合评价方法。

1 评价原理和方法

1.1 云模型

定义1[2]:假设U为一组正整数,其定义的一个质的定义为C,若有,它是C上的一阶随机实现,而C的隶属度是按某种规则的随机数,μ(x)∈[0,1]为一个具有一定分布规律的随机数,那么μ(x)在域U上的分布被简单地用云来表示,并且每个[x,μ(x)]都叫一个云滴。

云模型由期望Ex、熵En和超熵He 3个数字特征组成,其中Ex表示的是n个云滴的期望,位于云图的重心;熵En是指定量概念的数值大小,它体现了定量概念的随机与模糊特性;He超熵是En中的一个熵,它体现了En的不确定性,它以云的厚薄及频散来表示。本文提出了一种基于直线段的“黄金分割”概念,即“黄金分割”概念。将[Xmin,Xmax]作为由专家确定的活动域,其中t为一个整数,通常为一个奇数。利用修正的“黄金分割”方法[9],得到了t朵云。语言术语集S={si∣i=-(t-1)/2,…,-1,0,1,…,(t-1)/2},t为整数且一般情况下为奇数。根据改进的黄金分割法[9],可以生成t朵云,其中最左云、中间云以及右云分别为Y-(t-1)/2(Ex-(t-1)/2,En-(t-1)/2,He-(t-1)/2)、Y0(Ex0,En0,He0)、Y+(t-1)/2(Ex+(t-1)/2,En+(t-1)/2,He+(t-1)/2)。通过论域可以计算云模型的期望值为

(1)

通过计算最右云和中间云的期望值,将这两个值作为线段的两端,其余根据黄金分割比率进行计算。对于云模型的熵值则需要满足:

En-1=En+1=0.382×(Xmax-Xmin)/6

(2)

针对云体模式,先给出云体的超熵量He0,再用黄金分割方法计算其超熵。

定义2[8]:将U定义为一个可计数的域,毕达哥拉斯的模糊云团Y是一个在U上的一个定性的定义,它也包含了一个关于云模式的3种数学特性:期望Ex、熵En和超熵He。毕达哥拉斯的模糊云特征为(,En,He)。

1.2 毕达哥拉斯模糊集

模糊集是由Zadeh[10]于1965年提出的概念,来处理一些模糊性的问题。此后,Atanassov[11]于1986年首次引入了直觉模糊集合,从而对其进行了广泛的研究。该方法综合了隶属、非隶属、犹豫3种不同类型的知识,在解决模糊与不确定问题时更加灵活、实用。由于客观事物所具有的复杂性和不确定性,有关直觉模糊数的研究已引起了人们的高度重视,也被广泛应用于诸多领域之中。直觉模糊集应用条件具有一定的严苛性,这就造成了它的适用领域有限,只适用于优属值和非优值之和大于1时的问题。基于这一思想,Yager[12]引入了毕达哥拉斯型模糊集合,并将其用于解决某一种类型的决策问题。Yager[12]在此基础上提出了毕达哥拉斯模糊集的概念,使得应用于隶属度与非隶属度两者平方和小于等于1的决策问题中。

定义3[13]:将一组语言设定为S={si∣i=0,1,…,t},代表一种语言词汇,st与s0代表一种语言词汇的上、下界,t+1为奇数,如果i>j,那么si>sj。

定义4[14]:设X是一个可枚举域,将B=(|x∈X)称作毕达哥拉斯模糊语言集上的一个非空集合X。其中μA(x)∈[0,1],vA(x)∈[0,1]分别代表x对于毕达哥拉斯语言值sθ(x)的隶属和非隶属程度,并满足∀x∈X,0≤[μA(x)]2+[vA(x)]2≤1。

定义5[15]:

(3)

式中:μb1和νb1为隶属度和非隶属度的代表。

2 基于组合赋权-云模型的毕达哥拉斯模糊语言的综合评价方法

基于云模型理论,将毕达哥拉斯模糊数引入决策环境和云模型中。为了避免专家依靠经验确定的由于主观性过大,忽略了客观因素,只考虑了单个的目标权重,忽略了各个因素的重要程度,从而造成了与现实的偏离,提出一种基于博弈论组合赋权的、毕达哥拉斯模糊云模型相结合的综合评价方法。其具体评价方法流程如图1所示。

图1 决策流程

2.1 G1法确定主观权重

G1法是一种基于层次分析法(analytic hierarchy process, AHP)进行改进的主观赋权法,其无需进行一致性检验,计算简便直观且节省计算量,其具体计算步骤如下。

(1)确定指标序关系。各专家按指标x1,x2,…,xm的重要性由大到小对指标集进行排序,得到指标序关系:

(4)

(2)确定指标xk-1与xk相对重要度的比值。由专家给出指标xk-1与xk相对重要度比值rk的重要性评分表,见表1。

(5)

表1 rk赋值参考

(3)计算指标权重系数ωk。

(6)

ωk-1=rkωk

(7)

2.2 CRITIC法确定客观权重

CRITIC法是一种以指标对比强度和冲突性为基础的客观赋权法,兼顾权重的关联性和变异性,综合了熵权法和相关系数法的优势,充分挖掘数据的信息量使计算结果更加合理,其具体计算步骤如下。

(1)计算各指标的标准差σj。

(8)

(2)计算各指标之间的相关系数。

(9)

(3)计算指标的信息量Ij。

(10)

(4)计算各指标的客观权重ωj。

(11)

2.3 基于博弈论组合赋权

假定用q种方式给m个指数赋权,也就是获得了q个性质指数的权向量。假定uk=(uk1,uk2,…,ukm),k=1,2,…,q,uk就是一个基础权向量集合。利用G1方法与CRITIC方法得到各指标的综合权值,采用对策论方法对各指标进行综合评价。

(1)对每一种基础加权向量进行线性合并,得到一组加权向量,其中ui=(u1,u2,…,ui)u=1,2,…,n,那么若干基本加权向量的任何一种线性组合为

(12)

(2)通过最大限度地减小u和每一个变量之间的偏差,从而得到最佳权重向量:

(13)

(3)对上述问题进行集合,形成一个由多个指标组成的交错优化模型,使多重加权分配与该模型得到的结论达到全局的平衡。上述公式的解法可以用一条直线方程式来表达[16],即

从而得到一种线性合成系数εi。并作归一化处理得到

(14)

(4)求出对G1和CRITIC求出的权重进行优化组合得

(15)

2.4 基于组合赋权-毕达哥拉斯模糊云模型

(16)

将项目在属性值下的毕达哥拉斯模糊型云滴(,Enij,Heij)为基础,从而进行信息集结,通过对每一种类型的属性加权w={w1,w2,…,wm},得出该项目xi的毕达哥拉斯式的模糊云(,Eni,Hei)。

在此基础上,每个数值特性的数值计算公式为

(17)

其中,还存在对隶属和非隶属两种数值的计算:

3 案例分析

3.1 案例背景

某企业是我国一家物流运输企业。现如今我国物流竞争日益激烈,顾客需求更加多元化。因此该企业提出响应时代发展趋势进行数字化转型,通过数字化转型来实现企业更高效运作。在企业数字化转型之前需要对其数字化转型的风险进行预估评价,从而更好地进行数字化转型。该企业人员首先要通过分析物流企业的数字化转型可能面临的风险,来针对性地建立相应的评估指标体系。Muller等从经济、社会、技术、IT(信息计算)、政策5个方面对数字化转型风险进行划分[18]。依据相关单位风险评估报告和前人的研究,初步构建出物流企业数字化转型风险的评估指标体系,包含经济风险C1、社会风险C2、技术风险C3、IT风险C4、政策风险C5。从这5个方面构建出基础的一级评估指标,而后确定评价标准进行评价分析。

3.2 构建评价标准云

将我国物流企业数字化改造风险评估的结果标准分为低风险、低风险、中风险、较高风险、高风险5个级别,相应的评分区间为[0,1],评分值较大,表示风险较大,且安全程度较低。

云生成方法见表2,其中He0=0.008,Xmin和Xmax对应于评分取值范围,在表3[19]中显示了按照该法则进行运算得到的特定级别的数值特征值,并且按照表3构造了对应的基准评价云图,如图2所示。

表2 云生成方法[19]

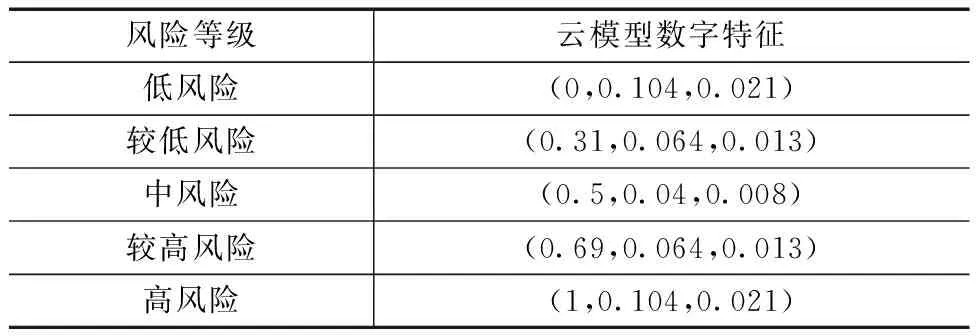
表3 各风险等级云数字特征

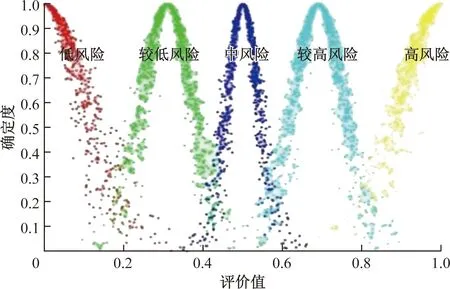
图2 标准评估云图

3.3 初始决策数据

本次公司决策共有3个专家ei(i=1,2,3)进行决策,其具体给定论域[0,1],给定He0=0.1,利用定义5和表1生成对应的毕达哥拉斯模糊云决策矩阵见表4。

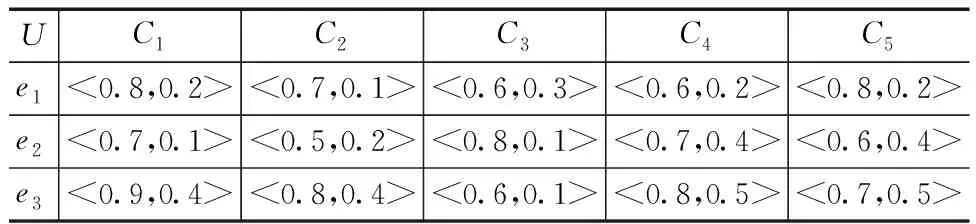
表4 决策者的决策信息

4 结果分析

4.1 数据结果计算

通过式(4)～式(7)得到G1的主观权重,通过式(8)～式(11)得到CRITIC客观权重,再通过式(12)～式(15)博弈论法得到其组合权重。根据3个专家其所属的不同领域类别确定3个专家的权重分别为0.25、0.35、0.40。具体权重见表5。

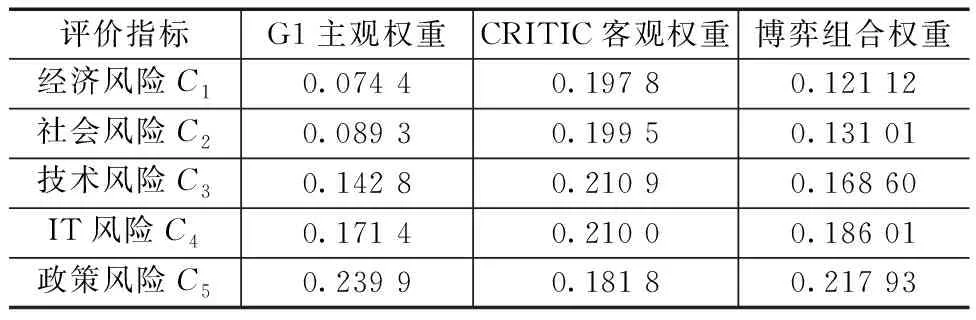
表5 准则层各指标权重

通过式(16)、式(17)得出各指数的数值特性。并与各指数的加权相结合,得出一个完整的云图的数值特征(<0.505 5,0,710 3,0.288 4>,0.097 5,0.024 7)。各指标云模型风险状况见表6。

4.2 数据结果分析

结合上述数据通过MATLAB绘制出各待测指标相应的风险评价云和标准云的对比,如图3所示,其中黑色部分为具体指标所对应的曲线,并结合图形进行分析。

通过表6数据以及图3指标云图可以看出物流企业数字化转型过程中,对于物流企业来说IT风险和政策风险属于中等风险,然而经济风险、社会风险和技术风险在企业的数字化转型过程中则属于较高的风险,需要企业提前充分准备及时作出预防措施。

最后得到物流企业数字化转型的风险综合评估云图,如图4所示,通过计算得出最终的综合评估云为中等风险。即该物流企业数字化转型过程的风险评估结果为中等风险,以及需要在各别指标上进行相应不同程度的预防。

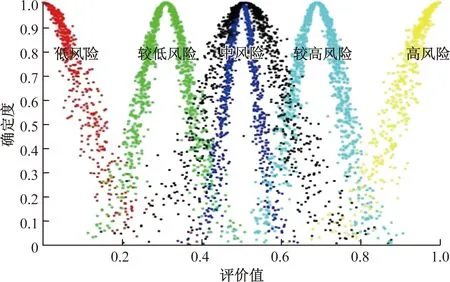
图4 综合评估云图

4.3 不同评估方法结果比较

为了更好地验证上述结论,说明本文提出的方法的有效性,也为了说明本文提出方法与其他方法的差异性,选取AHP-模糊综合评价[20],得到的结果为中等风险,与本文相同。还选取了灰色评估[21],但其结果为较低风险,与本文结果有少许差别,还选取了熵权-云模型[22]评估方法,与本文结果一致也为中等风险,具体结果汇总见表7。

表7 不同评估方法的结果

从表7中可以看出,其他3种评价方法所得到的结论与所提出的方法相吻合,从而说明了采用毕达哥拉斯模糊综合赋权-云模型进行综合评判的可行性。通过对本文中给出的例子的分析,本文方法优点在于:模糊性语言解决了决策中有些数据难以准确表示的问题,且通过组合权重解决了单一权重可能导致的偏差,使评价结果更准确,通过云图更直观地呈现评价结果。

5 结语

通过将毕达哥拉斯模糊理论与云模型理论相结合,创新性地采用主观客观博弈组合赋权,提出了一种基于组合赋权和云模型的毕达哥拉斯模糊语言综合评价方法。并引用一个实例,建立对应评价指标体系,依据方法和步骤,解决相应的评价问题。该方法主要特点为:①通过主观权重和客观权重的博弈组合赋权,克服了单一权重可能导致的信息损失;②通过将云模型引入综合评价中,通过云图更为直观地展现评估结果;③引入了毕达拉斯模糊数与云模型相结合,有效地改善了评价对象具有的模糊性、随机性以及不确定性等问题。

通过具体评估得出风险结果,并与其他评估方法进行对比,论证了本方法的有效性和合理性,也提供了更多构建模糊评级的可能性。