基于测试代价的三支邻域属性约简算法

张欣蕊 万仁霞 岳晓冬 陈瑞典

摘 要：针对粗糙集属性约简时很少考虑属性自身的测试代价等问题，提出了一种基于测试代价的三支邻域属性约简算法。算法根据各属性在邻域分辨矩阵中出现的频次和比例来计算属性重要性，并结合属性自身的测试代价来构造性价比指标，以此指导属性的甄选。三支决策方法被用于划分属性集，为属性的约简处理提供数据支撑。在7个UCI公共数据集上进行对比实验，结果表明，该算法可得到比对比算法更小的属性约简集合，在分类精度不降低的情况下，该算法具有更少的运行时间和更小的测试代价。基于财政收入的预测应用实例进一步证明了所提算法的有效性和实用性。

关键词：邻域粗糙集； 邻域分辨矩阵； 属性约简； 测试代价； 三支决策

中图分类号：TP391   文献标志码：A

文章编号：1001-3695（2024）03-028-0836-06

doi：10.19734/j.issn.1001-3695.2023.06.0306

Three-way neighborhood attribute reduction algorithm based on test cost

Zhang Xinrui1， Wan Renxia1， Yue Xiaodong2， Chen Ruidian3

（1.College of Mathematics & Information Science， North Minzu University， Yinchuan 750021， China; 2.School of Computer Engineering & Science， Shanghai University， Shanghai 200444， China; 3.Institute for Big Data in Health Fujian Hongyang Software Co.， Ltd.， Fuzhou 350002， China）

Abstract：In order to address the issue of test cost being rarely considered in rough set attribute reduction， this paper proposed a three-way neighborhood attribute reduction algorithm based on test cost. The proposed algorithm calculated the attri-bute importance according to the frequency and proportion of each attribute in the neighborhood resolution matrix， and combined the test cost of the attributes to construct the the cost performance index to guide the selection of attributes. Three-way decision-making method was employed to partition attribute sets， which provided data support for the attribute reduction process. Comparative experiments were conducted on seven UCI public datasets， which demonstrate that the proposed algorithm yields a smaller attribute reduction set compared to the comparison algorithm. Moreover， the proposed algorithm exhibited a shorter running time and lower test cost without compromising classification accuracy. Furthermore， it provided an application example based on fiscal revenue prediction to further validate the effectiveness and practicality of the proposed algorithm.

Key words：neighborhood rough set; neighborhood resolution matrix; attribute reduction; test cost; three-way decisions

0 引言

1982年，粗糙集理论由Pawlak教授［1］首次提出。这是一种用来处理不确定、不精确信息的新型数学方法。 粗糙集理论［2］利用上下近似的方式对集合进行刻画，并把整个论域划分为三部分。基于此，Yao［3］提出了三支决策的思想，认为从正域中得到的规则表示对决策的接受，从边界区域获得的规则代表了决策的延迟，从负域得到的规则表示对决策的拒绝。三支决策思想的提出，为将粗糙集理论运用到实际的决策问题上提供了理论依据。

属性约简［4］是粗糙集领域研究的一项重要内容，其目的是在保证属性集合对知识库划分能力不变的前提下，对冗余属性进行删除。基于等价关系提出的粗糙集模型只能对离散型数据进行处理，而在实际应用中却有大量的连续数据集合［5］。因此，Lin［6］在信息粒化、粒度的基础上提出邻域关系。胡清华等人［7］基于Lin的研究成果，提出了一种邻域粗糙集模型，用邻域关系代替原有的等价关系来处理连续型數据。在属性约简过程中，能否准确度量属性重要性十分关键。典型的属性重要性定义方法主要有基于Pawlak［8］和基于条件熵［9］两类。但这两种方法度量的都是核属性重要性，而非核属性的重要性均为零。叶军等人［10］以分辨矩阵为基础，提出了一种新的属性重要性定义方法。该方法既能度量核属性重要性，也能度量非核属性重要性，避免了非核属性重要性都为零的情况。季雨瑄等人［11］把等价关系下的分辨矩阵拓展到邻域粗糙集中，属性的重要性函数是根据条件属性在邻域分辨矩阵中出现的频次和比例而构造的，并以此作为启发性因子，提出了一种新的启发式属性约简算法。

上述模型都是以精度为目标，但实际应用中不仅需要关注数据的分类精度，也要关注获取数据的代价，即测试代价［12］。虽然属性集越多，分类精度会越高，但同时也会增加测试代价［13］。因此，在属性约简的过程中需要考虑测试代价，只有这样才能使算法更加适应实际问题。刘琼等人［14］重新定义了基于区间值邻域的熵结构，构造了区间值系统下的代价敏感函数，并提出了基于代价敏感的区间值特征选择方法。Fang等人［15］基于三支决策和分辨矩阵，提出了解决测试代价近似属性约简问题的框架，并设计了测试代价属性约简算法的添加策略和删除策略。文献［16～18］研究了基于测试代价的约简算法，用于解决多属性约简问题。

目前在邻域粗糙集中引入测试代价的研究较少。基于此，本文结合三支决策思想，将测试代价融入邻域粗糙集下的属性约简算法，提出了一种基于测试代价的三支邻域属性约简算法。

1 预备知识

1.1 邻域粗糙集

定义1［7］ 给定论域U={x1，x2，…，xn}，C为条件属性，D为决策属性，V是属性值的集合，f=U×（C∪D）→V是信息函数，δ（0≤δ≤1）为邻域半径，则称NDS=（U，C∪D，V，f，δ）是一个邻域决策系统。

3.2 邻域半径δ取值分析

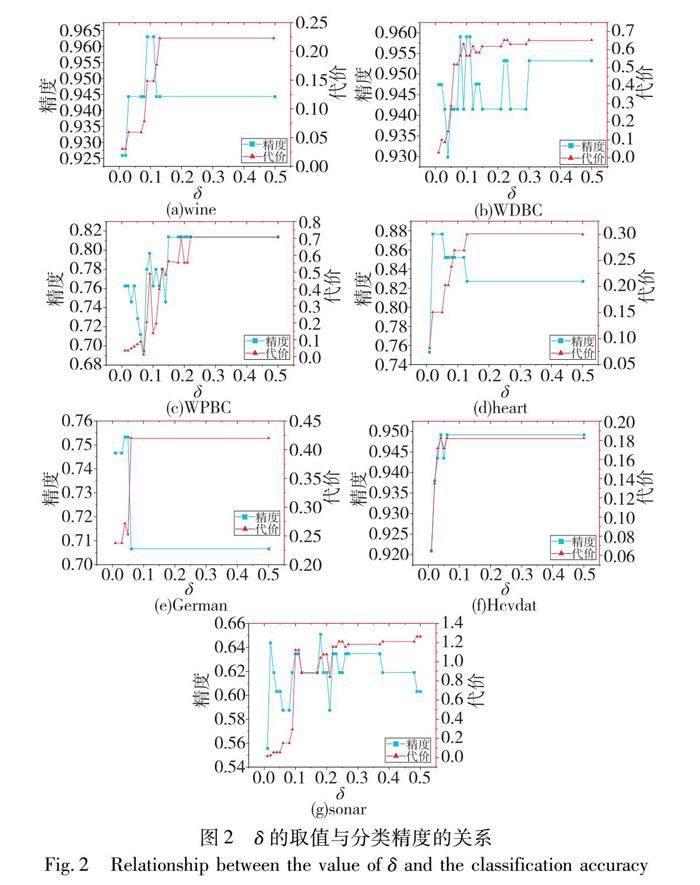
δ的取值直接影响属性约简的结果。在不同的δ取值下，算法得到的属性约简不同，这会造成根据属性约简进行分类后得到的分类精度不同［21］。本文在［0，1］内按0.01增进，采用高斯朴素贝叶斯分类算法，δ取值与分类精度的关系如图2所示。

图2（a）～（h）描述了在不同的δ取值下，数据集约简后的分类精度和获取相应属性所需代价值。随着δ的增大，各数据集的分类精度和属性代价最后均趋于稳定并涵盖了属性集合中的所有属性。由图2可知，当δ取值为0.03～0.05时，数据集的分类精度较高且属性代价较小，本文选取δ=0.05。

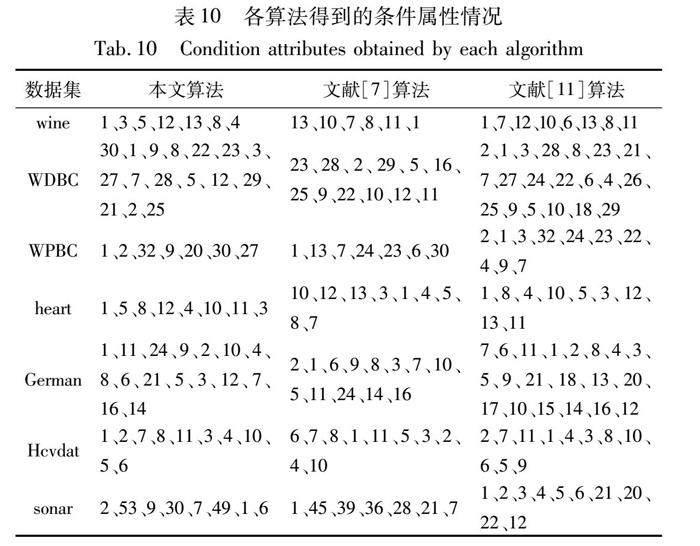
3.3 实验结果分析

将本文算法与文献［7，11］算法进行对比，三种算法进行属性约简后所得条件属性情况如表10所示。从表10可以发现，本文算法与文献［7，11］算法约简后得到的条件属性个数均有明显减少，说明三种算法都可以达到属性约简的目的，具有有效性。分别使用这三种算法对数据集进行属性约简， 统计各自对应的属性约简长度、测试代价、分类精度和运行时间。实验结果如图3～6所示。

观察图3可知，本文算法得到的属性约简长度均小于文献［11］的约简长度。在wine、WDBC、German、sonar数据集中，虽然本文算法的约简长度大于文献［7］，但在WPBC和Hcvdat数据集中，本文算法和文献［7］得到的属性约简长度相同，在heart数据集中，本文算法得到的属性约简长度在三种算法中最短。由图4可知，本文算法所得约简测试代价最小。在图5中可以发现，三种算法的分类精度较为接近且精度较高。图6中，代表本文算法的折线整体位于其他两条折线的下方，说明本文算法在运行过程中所用时间最短，效率最高。

综上可知，相较于文献［7，11］算法，采用本文算法进行属性约简后得到的属性约简个数适中，分类精度较高且运行时间较短。

4 实例分析

为了验证本文算法的实用性，将其应用在财政收入预测中。所采用的数据均来自《国家统计年鉴》，数据时间为2000—2021年，详细数据如图7所示。参考相关文献资料［22］，选取13个影响财政收入（y）的主要因素。

本文选择了13个可能影响财政收入的指标，数据维度较多，需要对数据进行降维处理。假设本章数据集中各属性的测试代价全部服从N（0.02，0.01），据此随机生成属性测试代价，具体数值如表11所示。

分别使用本文构建的属性约简算法、文献［7，11］算法对影响财政收入的因素进行约简，结果如表12所示。

根据表12可以发现，本文构建的基于测试代价的三支邻域属性约简算法得到的属性约简集合付出的代价最小，且算法的运行时间最短。

基于本文构建的基于测试代价的三支邻域属性约简算法得到的约简结果，将影响财政收入的影响因素由初始的13个缩减为3个，分别为就业人员总数x1、城镇居民人均消费性支出x2、年末总人口x3。将这三个因素作为多元线性回归模型的样本特征，构建多元线性回归模型，得到我国财政收入预测模型为

y=0.033+4.488x1+1.591x2-5.802x3（17）

由表13中F检验的结果分析可以得到，显著性P值为0.000***，水平上呈现显著性，拒绝回归系数为0的原假设，因此模型基本满足要求。

我国财政收入预测模型的拟合效果图如图8所示。

由表14可知，我国财政收入预测模型的平均相对误差为0.082，R2为0.995，调整后R2为0.994，说明采用本文算法的财政收入预测模型平均误差较小且拟合质量高，模型具有良好的参考性和应用价值。

5 结束语

本文将三支决策思想融入邻域粗糙集属性约简算法中， 提出一种基于测试代价的三支邻域属性约简算法。算法利用各属性在邻域分辨矩阵中出现的频次及比例计算属性重要性，并在此基础上考虑属性的测试代价构造性价比指标，以此作为三支决策的评价函数，对属性进行三分。算法有效地解决了属性约简问题，与同类算法相比，还具有运行时间短、分類效率高的特点。最后，将本文算法应用于财政收入预测中，得到的财政收入预测模型通过了F检验，平均误差较小且拟合程度较好，说明了本文算法的有效性和实用性。

由于UCI数据集中并没有给出各个属性相应的测试代价，所以经常采用分布函数随机生成测试代价。不同的测试代价分布会对约简结果产生影响。常用的测试代价分布有均匀分布、正态分布和帕累托分布。为方便计算，本文中采用正态分布函数生成测试代价。后续工作中，将研究采用均匀分布函数和帕累托分布函数生成测试代价时本文算法的约简性能。

参考文献：

［1］Pawlak Z. Rough sets［J］. International Journal of Computer and Information Sciences， 1982，11（5）： 341-356.

［2］胡成祥， 张莉， 黄晓玲， 等. 面向属性变化的动态邻域粗糙集知识更新方法［J］. 山东大学学报： 理学版， 2023，58（7）： 37-51. （Hu Chengxiang， Zhang Li， Huang Xiaoling， et al. Dynamic neighborhood rough sets approaches for updating knowledge while attributes generalization［J］. Journal of Shandong University： Natural Science， 2023，58（7）： 37-51.）

［3］Yao Yiyu. Three-way decisions with probabilistic rough sets［J］. Information Sciences， 2010，180（3）： 341-353.

［4］Wang Zhen， Shi Chengjun， Wei Ling， et al. Tri-granularity attribute reduction of three-way concept lattices［J］. Knowledge-Based Systems， 2023，276.

［5］杨洁， 匡俊成， 王国胤， 等. 代价敏感的多粒度邻域粗糙模糊集的近似表示［J］. 计算机科学， 2023，50（5）： 137-145. （Yang Jie， Kuang Juncheng， Wang Guoyin， et al. Cost-sensitive multigra-nulation approximation of neighborhood rough fuzzy sets［J］. Computer Science， 2023，50（5）： 137-145.）

［6］Lin T Y. Granular computing on binary relations I： data mining and neighborhood systems［J］. Rough Sets in Knowledge Discovery， 1998，1（1）： 107-121.

［7］胡清华， 于达仁， 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简［J］. 软件学报， 2008，19（3）： 640-649. （Hu Qinghua， Yu Daren， Xie Zongxia. Numerical attribute reduction based on neighborhood granulation and rough approximation［J］. Journal of Software， 2008，19（3）： 640-649.）

［8］盛茹雪， 李红宇， 姜春茂， 等. 一种基于序贯三支决策的属性约简方法研究［J］. 模糊系统与数学， 2021，35（6）： 48-65. （Sheng Ruxue， Li Hongyu， Jiang Chunmao， et al. An attribute reduction method based on sequential three-way decision［J］. Fuzzy Systems and Mathematics， 2021，35（6）： 48-65.）

［9］张晓燕， 匡洪毅. 区间值序决策表的条件熵属性约简［J］. 山西大学学报： 自然科学版， 2023， 46（1）： 101-107. （Zhang Xiao-yan， Kuang Hongyi. Attribute reduction based on conditional entropy in interval valued ordered decision table［J］. Journal of Shanxi University： Natural Science， 2023，46（1）： 101-107.）

［10］叶军， 朱华生， 黎敏. 一种属性重要性定义方法及其在约简中的应用［J］. 计算机应用研究， 2016， 33（7）： 2075-2078，2086. （Ye Jun， Zhu Huasheng， Li Min. A kind of attribute importance defined method and its application in attribute reduction［J］. Application Research of Computers， 2016，33（7）： 2075-2078，2086.）

［11］季雨瑄， 葉军， 杨震宇， 等. 结合分辨矩阵改进的邻域粗糙集属性约简算法［J］. 山东大学学报： 工学版， 2022，52（4）： 99-109. （Ji Yuxuan， Ye Jun， Yang Zhenyu， et al. An improved neighborhood rough set attribute reduction algorithm combined with resolution matrix［J］. Journal of Shandong University： Engineering Science， 2022，52（4）： 99-109.）

［12］吴迪， 廖淑娇， 范译文. 协调多尺度决策系统中基于测试代价的属性与尺度选择［J］. 模式识别与人工智能， 2023，36（5）： 433-447. （Wu Di， Liao Shujiao， Fan Yiwen. Attribute and scale selection based on test cost in consistent multi-scale decision systems［J］. Pattern Recognition and Artificial Intelligence， 2023，36（5）： 433-447.）

［13］吕艳娜， 苟光磊， 张里博， 等. 深度置信网络的代价敏感多粒度三支决策模型研究［J］. 计算机应用研究， 2023，40（3）： 833-838. （Lyu Yanna， Gou Guanglei， Zhang Libo， et al. Research on cost-sensitive multi-granularity three-way decision model for deep belief network［J］. Application Research of Computers， 2023，40（3）： 833-838.）

［14］劉琼， 代建华， 陈姣龙. 区间值数据的代价敏感特征选择［J］. 南京大学学报： 自然科学版， 2021，57（1）： 121-129. （Liu Qiong， Dai Jianhua， Chen Jiaolong. Cost-sensitive feature selection for interval-valued data［J］. Journal of Nanjing University： Natural Scicence， 2021，57（1）： 121-129.）

［15］Fang Yu， Min Fan. Cost-sensitive approximate attribute reduction with three-way decisions［J］. International Journal of Approximate Reasoning， 2019，104： 148-165.

［16］张清华， 庞国弘， 李新太， 等. 基于代价敏感的序贯三支决策最优粒度选择方法［J］. 电子与信息学报， 2021，43（10）： 3001-3009. （Zhang Qinghua， Pang Guohong， Li Xintai， et al. Optimal granularity selection method based on cost-sensitive sequential three-way decisions［J］. Journal of Electronics & Information Techno-logy， 2021， 43（10）： 3001-3009.）

［17］邓大勇， 刘月铮， 肖春水. 决策系统簇的平均代价敏感并行约简［J］. 浙江师范大学学报： 自然科学版， 2023，46（1）： 7-17. （Deng Dayong， Liu Yuezheng， Xiao Chunshui. A study of average cost-sensitive parallel reducts in a family of decision systems［J］. Journal of Zhejiang Normal University： Natural Science， 2023，46（1）： 7-17.）

［18］刘鑫， 胡军， 张清华. 属性组序下基于代价敏感的约简方法［J］. 南京大学学报： 自然科学， 2020，56（4）： 469-479. （Liu Xin， Hu Jun， Zhang Qinghua. Attribute reduction based on cost sensitive under attribute group order［J］. Journal of Nanjing University： Natural Science， 2020，56（4）： 469-479.）

［19］Fang Yu， Gao Cong， Yao Yiyu. Granularity-driven sequential three-way decisions： a cost-sensitive approach to classification［J］. Information Sciences， 2020，507： 644-664.

［20］Yao Yiyu. Three-way decisions and cognitive computing［J］. Cognitive Computation， 2016，8（4）： 543-554.

［21］Li Baizhen， Wei Zhihua， Miao Duoqian， et al. Improved general attribute reduction algorithms［J］. Information Sciences， 2020，536： 298-316.

［22］任晶晶， 高上彬. 基于SVR的吕梁市地方财政收入预测模型［J］. 信息技术与信息化， 2022 （1）： 46-49. （Ren Jingjing， Gao Shangbin. Prediction model of local fiscal revenue in Lyuliang based on SVR［J］. Information Technology and Informatization， 2022（1）： 46-49.）