双区型仓库订单分批与拣选协同优化研究

张艳菊 李群 张彭涵 李蕊

摘 要：針对订单分拣效率低下导致商品出库缓慢的问题，提出一种基于双区型仓库订单分批与拣选的协同优化模型，设计求解模型的CWDP-BSA（clarke-wright and dynamic programming & backtracking search algorithm）协同优化算法。在节约算法中引入快速排序法对订单组合的距离节约值排序，考虑AGV承载量，运用多阶段决策过程最优策略得出状态转移方程求解订单分批模型，确定初始分批方案；并采取多因子选择的回溯搜索算法求解拣选路径模型，以此确定初始拣选方案。再以以上两方案为基础，建立新的基于订单时间窗的订单分批和拣选协同优化模型并求解，进一步优化订单分批和拣选方案。最后通过对比实验得出，平均每批次订单的拣选距离减少了约24.56%，优化后的拣选时间比优化前缩短了约11.4%，在求解不同规模算例时，CWDP-BSA算法的求解结果优于CPLEX软件和其他算法，验证了模型与算法的稳定性和有效性。实验表明，协同优化后的订单分批与物品拣选策略能够有效提升订单出库效率。

关键词：双区型仓库； 订单分批拣选； 协同优化； 节约算法； 回溯搜索优化算法； CWDP-BSA算法

中图分类号：F252;TP18   文献标志码：A

文章编号：1001-3695（2024）03-015-0746-10

doi：10.19734/j.issn.1001-3695.2023.07.0326

Research on collaborative optimization of order batching andpicking in two-block warehouse

Zhang Yanjua，b，c， Li Quna， Zhang Penghana， Li Ruia

（a.School of Business Administration， b.Management Science & Engineering Research Institute， c.Modern Enterprise System Innovation Research Center， Liaoning Technical University， Huludao Liaoning 125105， China）

Abstract：In response to the problem of slow delivery of goods due to low order sorting efficiency， this paper proposed a collaborative optimization model based on two-block warehouse order batching and picking，and designed a multi-stage CWDP-BSA algorithm to solve the model. In the saving algorithm， it introduced quick sorting method to sort the distance savings of order combinations. Considering the carrying capacity of AGV， under the guidance of the optimal strategy in the multi-stage decision-making process，it obtained the state transition equation to solve the order batch model and determine the initial batch plan. And it adopted a multi factor selection backtracking search algorithm to solve the picking path model， in order to determine the initial picking plan. Based on the two schemes， establishing and solving a collaborative optimization model for order batching and picking based on order time windows were to further optimize order batching and picking schemes. Finally， through comparative experiments， it can reduce the average picking distance of each batch of orders by about 24.56%， and shorten the optimized picking time by about 11.4% compared to before. When solving examples of different scales， the CWDP-BSA algorithm performs better than CPLEX software and other algorithms， which verifies the stability and effectiveness of the model and algorithm. Experiments show that the collaborative optimization of order batching and item picking strategies can effectively improve the efficiency of order delivery.

Key words：two-block warehouse; order batch picking; collaborative optimization; Clarke-Wright algorithm; backtracking search algorithm; CWDP-BSA algorithm

0 引言

近年来，在线销售增长显著，订单向多品种、高频次、多样化的模式转变，涌现出了单笔订单规模小、订单总体数量大、品种数目多且响应时间严格等特点。同时，消费者对及时配送的要求也不断提高，加大了各电商企业的物流服务压力。相关研究发现，在整体的物流仓储系统中，拣选作业的劳动量占总作业量的60%［1］，而且传统的拣选方式效率低、错误率高［2］。可见，需要更加高效的拣选作业方法以提升物流仓储中心的运作效率，而分批和拣选环节所需时间占拣选作业总时间的比重最高，因此对订单分批和拣选效率提升的研究有着重要的实践意义。

国内外学者一般将订单分批策略和拣选路径规划作为独立的问题分别研究，均取得了较丰富的研究成果。有关订单分批策略的研究，订单批处理问题（OBP）的目标是将客户订单分组到相应批次中去，从而使通过矩形仓所有路程的总长度最小化［3］，对批次的合理排序可以最大程度地减少总作业时间。针对在线情景下的订单批处理问题，Cristiano等人［4］提出了适用于平行及两个或两个以上过道的矩形网格存储区的方法。Mehrdad等人［5］考虑了具有多个拣货员的在线订单批处理问题（OOBP），其中所有批次的最大完成时间须达到最小化。关于订单分批的方法，Cals等人［6］提出了一种深度强化学习（DRL）方法和启发式方法，通过分析怎样以及何时对客户的订单进行分批，从而提高作业效率，使订单准时到达。公斌［7］采用节约算法来解决城市物流配送路径优化问题。

有关拣选路径的研究，Namrata等人［8］解决了仓库中的拣选路径优化问题，最大限度地减少了旅行时间和距离。由于仓储位置和拣选路径问题是两个相互依赖的问题，Silva等人［9］建立了集成仓储位置与订单拣选问题的模型，并考虑了返回、S形、中点和最大间隙四种路由策略。针对多区型仓库的拣货路线优化问题，张水旺等人［10］对多区型仓库布局结构、拣选路径等问题进行了明确的定义，建立了多区型仓库下的拣货路线优化模型。关于路径规划的方法，Sebo等人［11］针对最小化拣货距离的问题，介绍了遗传算法的性能及其与其他路由策略（如启发式算法和给定假设下的算法等）的比较。翟梦月等人［12］提出了一种变邻域-禁忌搜索算法，分别通过改变商品种类的分散程度和商品种类-数量配比来规划订单拣选路径。

尽管订单分批和拣选路径的优化问题在学术界已有较为深刻的研究，但是考虑两者协同优化的研究相对较少。现有研究主要从其他作业环节的协同合作出发，唐坚强等人［13］针对订单拆分和限时配送問题进行研究，分析出了考虑多仓库订单拆分与异构车辆路径的联合优化方法。李彤等人［14］针对不确定需求下的循环取货问题，提出了多车型最优路径-装载协同优化的复合解决方案。通过上述研究可以发现，订单分批和拣选的现有研究成果对本文具有重要的指导意义，但仍存在一些不足：a）对于分批策略来说，从“货到人”和“人到货”两个角度出发，有学者考虑到采用节约里程法求解订单分批策略，但节约法更加强调路程的节约，忽视了行程中的时间因素，导致分批结果效率不高；b）对于拣选路径来说，优化路径的方法大多采用遗传算法、禁忌搜索算法等，实际上这类优化方法效率并不高且容易陷入局部最优，需要寻找搜索能力更强的方法进行优化；c）对于协同研究来说，现有研究成果主要考虑了订单拆分和配送路径的协同，以及货物装载和配送路径的协同，关于订单分批与拣选路径的协同研究较少。

综上所述，针对双区型仓库背景下的订单分批与拣选路径问题，建立订单分批与拣选的协同优化模型，设计CWDP-BSA多阶段算法对模型进行求解。在实验分析部分验证了模型和算法的有效性与实用性。本文的主要创新点在于：a）为提升拣选作业效率，考虑订单分批和物品拣选是连续的整体过程，提出订单分批与物品拣选协同优化的解决思想；b）在模型构建方面，通过对拣选作业环节中各部分的关系进行耦合分析，进而提出订单分批和拣选路径协同优化的数学模型，该模型与传统拣选模型的区别在于，将订单分批和路径规划归为一个整体，并构建了两者间联系实现协同优化的思想；c）在算法求解方面，首先针对求解订单分批和拣选路径的优化方案集，设计了节约动态规划算法和回溯搜索优化算法，其次针对求解协同优化模型设计了多阶段算法CWDP-BSA。通过实验得出，目标值的波动处于±5%，验证了该协同优化算法的稳定性。同时，在真实数据集上进行实验分析，得出总拣选时间和拣选距离分别减少约11.4%和24.56%；利用合成数据集对分批次拣选时间和总拣选时间进行对比实验得出，CWDP-BSA算法的性能优于其他三种算法，验证了该协同优化算法的有效性。

1 问题描述及建模

1.1 问题描述

本文所研究的协同优化问题可以描述为：以双区型仓库为场景，在出库的所有流程中，对订单分批和拣选两个连续的工作环节进行协同优化，给出合理的分批方案和拣选路径方案，使某一规定时间段内n个订单能够完成拣选且拣选总时间最短。具体思路为：在订单分批时重点考虑AGV载重量，并规划距离较短的路径为初始分批和拣选方案；根据协同优化思想，由实际的订单时间窗划分最优分批和拣选方案，再依据方案进行拣选作业。一般流程为：AGV从仓库入口处出发，根据出库请求与优化后的拣选批次和拣选路线，分批次有序地进行拣选作业。具体订单分批和拣选处理流程如图1所示。

本文以双区型仓库为例，该仓库由两个布局相同的拣选区域和一定数量的等长巷道及货架组成，中间的主通道（过道）把仓库平均分为两个区，两边各有一条平行于主通道的边通道（过道和过道），相应的双区型仓库平面图如图2所示。设双区型仓库过道宽a=2 m，存储货位的长和宽分别为b=c=1 m，巷道之间的宽d=1.5 m，每一区域的巷道总数都是10条且每条巷道长度为10 m。每条巷道的两侧货位都可以进行拣选作业，每列又都包含3个垂直货位，即每排货架有60个货位，每条巷道左右两边的货位数为120个。给定每一个货物的储位编码方式为［区号，巷道，左右号，行号，货位号，体积］，巷道按照从左到右的顺序依次进行编码，每条巷道两侧的货位从前往后依次编码，分别表示为1，2，3，…，10，得到储位编码［x1，x2，x3，x4，x5，x6］。例如［1，3，1，2，10，1］表示1区第三条巷道的左侧第二行10货位，该待拣选点上的货物体积为1单位，出入口的编号是［0，0，0，0，0，0］。忽略拣选时的货位拣选垂直移动，拣选一个品项所需的时间为3 s，自动导引车的行走速度为1 m/s。考虑对双区型仓库订单分批与拣选协同优化问题的分析，给出相关定义如下：

定义1 拣选距离。拣选距离D为拣选所有批次商品经过的总距离，包括行走过道的距离d1、行走巷道的距离d2以及穿越货位的距离d3，即D=d1+d2+d3。给定［x1，x2，x3，x4，x5］和［x′1，x′2，x′3，x′4，x′5］为两个待拣选订单编号，则行走过道的距离d1=|x′1-x1|×a；将穿越巷道时两排货架的距离加入到计算中，那么行走巷道的距离d2=|x′2-x2|×（d+2b）；不考虑垂直方向的移动距离，穿越货位的距离d3分三种情况进行如下讨论：

a）当两个需要被拣选的货位是同一区域且同一巷道时，所要行走的距离为两个货位之间的距离，则d3=|x′3-x3-1|×c。

b）当两个待拣商品的货位在相同的区域而在不同的巷道时，行走距离的计算方法是取S形策略与混合型策略中的较小值，此时，给定d3=min{20-x′3-x3，x′3+x3-2}。

c）当两个待拣选商品的货位不在同一区域时，按照上述混合型策略进行求值，取值为两者之间的最小值，此时d3=min{|x′3-x3|，40-x′3-x3}。

定义2 拣选时间。拣选时间t是完成订单拣选动作的时间，包括寻找货品的时间ttravel和拣取货品的时间tpick，t=ttravel+tpick。通过降低寻找和拣取货品的时间可以减少总拣选时间t。

定义3 仓库网络。仓库网络由一个坐标图A（X，Y）表示，其中X为仓库过道长度，Y为两区域宽度。拣选过程的行走路径，即每条长与宽的边xr、yr都与拣选时间ttravel和tpick相关联。

定义4 自动导引车AGV。一辆自动导引车w=〈Cn，C〉有一个拣选订单的容量Cn和一个最大容量C（一辆AGV一次可以装载的最大货物体积）。W={w1，…，w|w|}代表所有的AGV。

定义5 请求。请求由r=〈sr，fr，or，pr，dr，tr，cr〉表示，其起点和终点分别为sr与fr，订单信息为or，最优排列批次为pr，AGV每次装载体积为cr，根据分批结果进行拣选得到的最小拣选距离为dr，最优拣选时间为tr。

定义6 路线。自动导引车的路线由Rw=〈l0，…，ln〉表示，l0，…，ln是Rw的起点和终点的有序序列，即li∈{sr|r∈Rw}∪{fr|r∈Rw}。如果一条路线是可行的，需满足：a）r∈Rw，sr在路线Sw中的fr之前；b）r∈Rw，w到达fr的时间较S形拣选策略更小，拣选时间达到最优；c）任何时候，已拣取并装载的货物体积（即请求的每批次大小）不超过自动导引车w的最大容量C。

示例1 为了更好地说明所研究问题，设置七个等待拣选的订单Or进行说明。

表1为订单信息，表2为根据拣选请求r得到的订单优化前后的分批结果、拣货路径。拣选请求r为：自动导引车w从Sr出发，根据订单信息O1～O7，在满足w=〈Cr，C〉的条件下求解最优排列批次pr，同时求出每批次最小拣选距离dr所在的拣选路线Rw，履行每批次拣选路线Rw，最终得出最优拣选时间tr，在完成订单分批与拣选后回到fr。

假设将订单以常用的顺序分批方法进行分批，在满足体积约束的条件下得到批次划分后，以S形行走策略为例对物品拣选的路径进行计算。图2的黑色部分为第一批次的商品储位，图中路线为第一批次的行走路线Rw1，灰色部分和阴影部分分别为第二、三批次的商品储位，那么，优化前分批次拣选路线如图3（a）～（c）所示，计算出优化前第一批次的总时间t1，即ttravel+tpick=139 s，第二、三批次的行走方式与第一批次相同，计算得出第二、三批次的总时间t2、t3分别为245 s、210  s。

而这种订单分批和拣选策略的效率并不高，依据拣选请求r，考虑将订单进行连接，把经过但没有出现在路线Rw上的订单按照次序插入到拣选路线中，直到全部的订单都被安排完拣选路线时结束。例如，将批次2中订单4编码［1，2，1，2，7，10］的货物插入至批次1中订单2编码［1，2，1，1，6，9］的货物后，不断插入直至每一批次拣选货物饱和，形成优化后的订单分批方案，如表2所示。根据新的分批方案，协同优化待拣选商品间的总距离，根据最短距离划定拣选路线，形成订单分批和拣选协同优化后的解决方案，如图3（d）～（f）所示。计算出优化后第一批次耗费的总时间t1=ttravel+tpick=149 s，第二、三批次的总时间t2、t3分别为146 s、95 s。可以看出，协同优化后的分拣总时间明显少于优化前所需要的总时间。由上述订单分批与拣选路径协同优化后所求得的结果可知，优化策略明显提高了作业效率。可以想象，随着订单规模的扩大，优化分批和拣选策略将会节省更多时间，说明传统分批方式与物品拣选策略存在弊端，本文提出的协同优化策略具有一定的可行性。

1.2 問题假设

为了减少非必要因素对分批和拣选问题的影响，使模型更具有针对性与实用性，同时起到简化模型构建与降低问题计算复杂程度的作用，对模型进行如下假设：a）每种商品仅有一个存储的位置；b）每个订单中的商品仅属于一个批次，不被分割到两个批次中；c）不将货物在货架上的垂直移动纳入拣选距离的计算中，垂直移动距离不会对拣选人员的拣选距离产生影响；d）所有的AGV从入口统一出发，拣选完成后返回入口，整个过程形成一个闭合回路；e）不考虑紧急插单的情况；f）订单中拣选的商品不会出现缺货的情况。

1.3 模型的参数与变量

本文模型使用到的集合含义、参数说明分别如表3、4所示，决策变量如下：

3 实验结果与分析

3.1 实验介绍

本文CWDP-BSA协同优化算法使用MATLAB R2022b编程，采用CPLEX作为模型求解器，所有实验环境均在Intel CoreTM i7-6 500U CPU 64位计算机上运行。为了更好地对比较结果进行分析，本文基于某电商企业订单高峰期内记录的订单数据的实际情况，生成100个订单作为测试算例，商品数量总计576件，参数设置已在1.1节中详细阐述，提取部分订单数据如表5所示。

3.2 订单分批和拣选协同优化结果对比分析

根据本文的模型和算法，分别对双区型仓库中的原始分拣策略和协同优化策略进行比较分析：按照顺序分批的方式将100个订单进行分批，共分成37个批次，由于受AGV容量限制，每批次包含1～5个订单不等；按订单顺序进行划分，得到优化前的订单分批结果；在相同的情景与订单数量中，用本文算法再进行求解。优化前后的部分订单分批结果与优化后每批次订单的拣选路径如表6所示。

可以发现，采用CWDP-BSA协同优化算法得出的结果与采用顺序分拣策略所得结果有显著不同。在CWDP-BSA协同优化算法中，将一个时间段看作时间窗，在该时间窗内到达的订单不是按照订单到达的时间顺序进行批次划分，而是综合考虑这一段时间内的所有订单，把订单中所包含商品的体积作为考虑因素，并将同一订单中的商品作为一个整体来进行相应的批次划分，得出优化后的订单分批结果，再根据协同优化思想使每一批次订单在一条最优最短的路径上完成拣选工作，从而使所有批次订单拣选总距离最小，同时花费更低的拣选时间。本节针对拣选距离和拣选时间，将100个订单的算例分别采用CWDP-BSA协同优化方法和不涉及协同优化的顺序拣选策略进行对比实验。选取前10个批次的订单进行拣选距离对比分析，如表7所示。以批次5为例，优化前批次内订单包含18件商品，以S形拣选策略拣选商品的顺序分别为［1，6，2，2，1，4］→［2，5，1，3，4，6］→［2，6，2，1，8，4］→［1，7，2，1，1，4］→［2，7，1，2，3，3］→［2，7，2，3，2，7］→［2，2，1，3，1，6］→［1，4，2，2，1，10］→［2，4，2，1，6，7］→［2，3，2，1，1，10］→［2，7，1，2，2，7］→［2，4，1，3，2，6］→［1，5，1，3，6，10］→［2，3，1，2，6，7］→［2，4，2，1，4，7］→［2，7，1，1，5，6］→［2，3，1，2，9，4］→［2，1，1，1，6，1］，根据定义1中对拣选距离计算方程式的定义d=|x′1-x1|×a+|x′2-x2|×（d+2b）+|x′3-x3-1|×c，得出优化前批次5的拣选距离为248 m；使用CWDP-BSA算法优化后批次内所含订单的拣选顺序为［1，1，1，3，2，6］→［2，1，1，1，6，1］→［2，1，2，2，2，9］→［2，2，2，3，5，4］→［2，3，1，2，6，7］→［2，3，1，2，9，4］→［2，3，1，3，5，8］→［2，4，2，1，4，7］→［2，4，2，1，4，8］→［2，4，1，3，9，5］→［2，4，1，3，8，1］→［2，5，2，1，5，7］→［2，5，2，1，6，9］→［2，7，2，3，4，6］→［2，7，2，1，3，3］→［2，7，1，1，5，6］→［1，5，2，1，3，7］→［1，7，2，2，1，1］→［1，7，2，2，5，8］→［1，6，1，1，6，5］→［1，5，1，3，7，7］→［1，5，2，2，4，6］→［1，5，2，2，5，8］，经协同优化后，批次5中23件商品的拣选距离为191 m。与优化前的结果相比，虽然优化后批次内增加了5件商品，但商品的拣选距离却缩短了约22.98%，且10个批次订单拣选距离的平均优化百分比为24.56%，说明协同优化算法能够很好地缩短拣选距离，对降低拣选时间有较大的帮助。

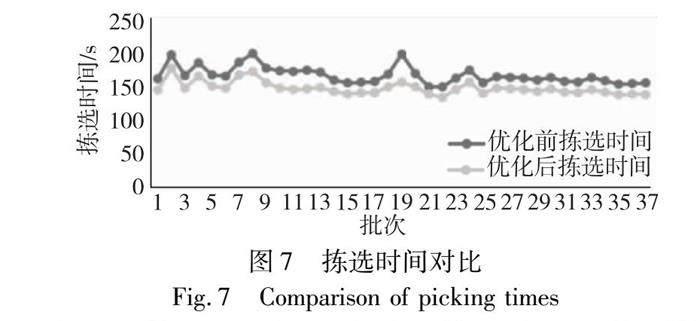
为了清晰地看出拣选作业缩短的时间，先求出初始未经过改进的分批与拣选路径所需时间，再求协同优化后每批次所需要的最短拣选时间，最后将每批次的最短拣选时间相加得到目标函数值，即拣选的最小总时间，对比结果如图7所示。

根据对比结果可以发现，在分批拣选时间上，协同优化后的每一个批次拣选时间都小于优化前，除了个别批次的时间优化百分比较低以外，剩余批次时间优化百分比均在10%～20%，具有明显的优化效果。在总拣选时间上，协同优化也呈现出了较好的优化效果，如表8所示的计算结果，在使用顺序分批和S形拣选策略的情况下，所计算的拣选总时间为6 267 s；经过订单分批和拣选路径协同优化后，所求得的最小拣选时间为5 551 s。由此可以计算出优化后的拣选时间比优化前缩短了716 s，也就是说，协同优化方法较初始分拣策略缩短了约11.4%的拣选作业时间，说明所提出的协同优化思路行之有效，能够得到合理的分批和拣选结果。

3.3 算法有效性分析

为验证不确定环境下的协同优化模型和CWDP-BSA算法的有效性，通过调整订单规模（Q）、订单商品种类（K）、AGV数量（W）三个参数，分别进行小规模仿真实验和大规模仿真实验。相关参数设置如表9所示。

3.3.1 小规模仿真实验

本节考虑订单商品种类多樣化、AGV自动导引车数量不定的特点生成随机数据，对10组订单规模为10的小算例进行测试。其中，Q为订单规模，K为商品种类，W为AGV数量，PT表示拣选总时间，RT表示运行时间，GAP表示CWDP-BSA算法求解结果与CPLEX求解结果的偏差，求解方法为（PT（CWDP-BSA）-PT（CPLEX））/PT（CPLEX）×100%。由于模型的约束条件和参数过多，在有限时间内，CPLEX求解器不能全部精确求解，部分算例也无法得到最优解，所以，本文设置CPLEX的最大运行时间限制为3 600 s，CPLEX和CWDP-BSA的小规模算例求解结果如表10所示。

以PT和RT为衡量指标，“*”表示两求解方法对比下更优的运行结果，GAP值表示CWDP-BSA算法的求解效果优于CPLEX。从结果来看，有6个算例的CWDP-BSA结果比CPLEX结果更优，拣选时间结果相差最大达7.08%；有4个算例的CWDP-BSA结果与CPLEX结果相同。从求解时间来看，CWDP-BSA的运行时间均小于或等于CPLEX。而CPLEX对于6个请求在

3 600 s内已经很难得到最优解，CWDP-BSA却可以在5 s内得到可接受的有效解，说明本文协同优化模型及CWDP-BSA算法行之有效。

为了验证算法的稳定性，使用CWDP-BSA协同优化算法和CPLEX求解器进行了10次运算。目标函数值波动情况如图8所示。该结果表明，在多次运算中两求解方法的目标值波动都处于±5%，但CWDP-BSA相较于CPLEX，求解波动更小，由此可以看出，本文方法的稳定性更好。

3.3.2 大规模仿真实验

在10次独立运算程序后，本节将实验求解所用的最大订单规模扩大到100个。为进一步验证算法的有效性，共进行两项实验，一是对CWDP-BSA和不同算法之间的效果进行比较，二是将本文协同优化算法和单独优化方法进行比较研究。

假设订单规模分别为10、30、50、70、100，其他参数相同的情况下，将CWDP-BSA算法与遗传算法（GA）、嵌套遗传算法（FNGA）进行对比实验。遗传算法是解决订单分批和拣选问题中最常用的方法，嵌套遗传算法在遗传算法的基础上进行改进，其收敛速度更快，文献［27］运用嵌套遗传算法进行运算，验证了其良好的收敛性和稳定性。在此基础上，本文将以上算法进行对比分析，如图9所示，结果发现CWDP-BSA算法和嵌套遗传算法比普通遗传算法效果更优，尽管嵌套遗传算法也能大大降低分批和拣选作业的时间，但所求得的拣选时间仍在任意订单规模中高于CWDP-BSA算法，该实验证明了CWDP-BSA算法的有效性。

为了验证协同优化研究的优越性，本文将CWDP-BSA算法与以下三种单独求解算法进行比较。所有对比算法均采用相同运行参数和环境，不同之处在于：算法A采用顺序分批和S形拣选策略，是仓库内常用的拣货方式；算法B采用CWDP节约与动态规划算法优化订单分批，采用S形拣选策略进行拣选作业；算法C采用BSA回溯搜索算法优化拣选路径，采用顺序分批的方式进行订单分批。三种算法均不涉及订单分批和拣选的协同优化。而算法CWDP-BSA采用CWDP算法优化分批方案，并采用BSA算法优化每一批次的拣选路径，使双区型仓库内的分拣作业得到协同优化。对各项算例取平均值作为实验结果，对比结果如图10所示。

通过对比实验结果可以发现，本文CWDP-BSA算法在分批次拣选时间和总拣选时间上都有较好的表现。用顺序分批和S形拣选策略且不涉及订单分批和拣选协同优化的算法A得到的分批次拣选时间和总拣选时间用时最长；单独优化分批方案的CWDP算法和单独优化拣选路径的BSA算法求解得出的拣选时间效果相似，CWDP比BSA算法性能好一些；采取订单分批和拣选协同优化的CWDP-BSA算法求解的分批次拣选时间和总拣选时间在四种算法中最短，并且表现出了良好的性能特征。具体实验结果如图10所示。

a）订单规模Q的作用。在AGV数量固定的情况下，随着订单规模的不断扩大，四种算法的分批次拣选时间和总拣选时间总趋势都在不断增加且总拣选时间的增幅较大，其中算法A所花费的拣选时间大于其余三种算法，算法C所得的拣选时间仅次于算法B，算法CWDP-BSA表现出更好的性能，在分批次拣选时间和总拣选时间上都低于其他算法。

b）商品种类K的作用。在订单规模固定的情况下，商品种类的增多会使订单中商品储位变多，从而使商品间位置更加复杂、拣选距离增加。然而，算法CWDP-BSA在商品种类不断增多时，分批次拣选时间和总拣选时间都低于其他三种算法，在总拣选时间上，CWDP-BSA算法节省的时间呈现出越来越多的趋势。

c）AGV数量W的作用。在订单规模固定的情况下，AGV数量的增多会直接对总拣选时间有明显的影响。由图10的实验结果可以发现，AGV数量增多使总拣选时间不断下降。算法A拣选时间最长，其次是算法B和C，算法CWDP-BSA的總拣选时间最短。由于每个批次只能由一辆AGV进行拣选，所以AGV总数量的变化不会对分批次拣选时间产生影响，但在此情况下，由CWDP-BSA算法求解的分批次拣选时间仍然低于其余三种算法，说明在该数据集中CWDP-BSA协同优化算法的求解效果优势明显。

4 结束语

本文针对仓库传统订单分拣作业效率低、成本高且订单量不断激增的现状，以拣选距离和拣选时间最小化为目标，建立协同优化模型并设计CWDP-BSA算法求解，最后通过实验验证了模型与算法的有效性，可得出以下结论：

a）考虑现有的订单履约流程，建立了针对订单分批与拣选的协同优化模型，所得出的订单分批和拣选方案能够有效提高拣选作业效率，降低双区型仓库的运营成本。

b）在所设计的CWDP-BSA协同优化算法中，将快速排序法与节约动态规划思想相结合，并采用多因子选择的回溯搜索优化算法得到订单批次和路径的初始解，基于订单时间窗约束得到分批和拣选方案的近似最优解。该方法有效增强了算法的寻优能力，提高了求解质量。

c）通过协同优化算法和单独优化算法的对比实验及不同规模下的算例实验，验证了CWDP-BSA协同优化算法的有效性和稳定性，为求解仓库订单分批和路径协同优化问题提供了新的有效算法。

本文考虑了固定订单情景下的订单分批与拣选路径协同优化的问题，而随着订单需求个性化的发展，未来研究可以将发生缺货、订单拆分或紧急插入等情况纳入考虑范围，以此进一步提高优化决策的科学性。

参考文献：

［1］Tompkines J A， White J A， Bozer Y A， et al. Facilities planning［M］. New Jersey： Wiley， 2003.

［2］Wang Yanyan， Wu Yaohua， Liu Peng. Sorting task optimization of automatic sorting system［J］. Journal of Mechanical Engineering， 2011，47（20）：10-17.

［3］Ivan ， Sergej K， Michael S. A hybrid of adaptive large neighborhood search and tabu search for the order-batching problem［J］. European Journal of Operational Research， 2018，264（2）： 653-664.

［4］Cristiano A V， John E B. Order batching using an approximation for the distance travelled by pickers［J］. European Journal of Operational Research， 2020，284（2）： 460-484.

［5］Mehrdad A， Yahia Z M， Ali M. A rule-based heuristic algorithm for online order batching and scheduling in an order picking warehouse with multiple pickers［J］. RAIRO-Operations Research， 2020，54（1）： 101-107.

［6］Cals B， Zhang Yingqian， Dijkman R， et al. Solving the online ba-tching problem using deep reinforcement learning［J］. Computers & Industrial Engineering， 2021，156： 107221.

［7］公斌. 城市物流配送系統改造更新的优化设计［J］. 统计与决策， 2009（3）： 60-63. （Gong Bin. Optimization design of urban logistics distribution system transformation and renewal［J］. Statistics and Decision， 2009（3）： 60-63.）

［8］Namrata S， Bhawesh S， Sung H C. Route optimization for warehouse order picking operations via vehicle routing and simulation［J］. SN Applied Sciences， 2020，2（2）： 311-329.

［9］Silva A， Coelho L C， Darvish M， et al. Integrating storage location and order picking problems in warehouse planning［J］. Transportation Research Part E， 2020，140： 102003.

［10］张水旺， 谢浩， 付林萍， 等. 考虑车载容量的多区型仓库拣货路径优化研究［J］. 系统科学与数学， 2021，41（1）： 238-253. （Zhang Shuiwang， Xie Hao， Fu Linping， et al. Research on optimization of picking path for multi zone warehouse considering vehicle capacity［J］. System Science and Mathematics， 2021，41（1）： 238-253.）

［11］Sebo J， Busa J J. Comparison of advanced methods for picking path optimization： case study of dual-zone warehouse［J］. International Journal of Simulation Modeling， 2020，19（3）： 410-421.

［12］翟梦月， 王征， 李延通， 等. 可移动货架仓储系统中商品储位分配问题研究［J］. 中国管理科学， 2023，31（3）： 167-176. （Zhai Mengyue， Wang Zheng， Li Yantong， et al. Research on the allocation of commodity storage space in mobile shelf storage systems［J］. Chinese Journal of Management Science， 2023，31（3）： 167-176.）

［13］唐坚强， 祁超， 王红卫. 带时间窗的多仓库订单拆分与异构车辆路径联合优化方法［J］. 系统工程理论与实践， 2023，43（5）： 1446-1464. （Tang Jianqiang， Qi Chao， Wang Hongwei. A joint optimization method for multi warehouse order splitting and heteroge-neous vehicle paths with time windows［J］. Systems Engineering-Theory & Practice， 2023，43（5）： 1446-1464.）

［14］李彤， 崔晶. 不确定需求环境下的路径-装载协同优化研究［J］. 系统工程理论与实践， 2021，41（10）： 2561-2580. （Li Tong， Cui Jing. Research on path loading collaborative optimization in uncertain demand environments［J］. Systems Engineering-Theory & Practice， 2021，41（10）： 2561-2580.）

［15］李曉春， 钟雪灵， 王雄志， 等. 双旋转货架拣货作业优化设计［J］. 管理工程学报， 2012，26（3）： 114-121. （Li Xiaochun， Zhong Xueling， Wang Xiongzhi， et al. Optimization design of picking operation for double rotating shelves［J］. Journal of Management Engineering， 2012，26（3）： 114-121.）

［16］Merve C T. A fuzzy multi-criteria approach based on Clarke and Wright savings algorithm for vehicle routing problem in humanitarian aid distribution［J］. Journal of Intelligent Manufacturing. 2023，34（5）： 2241-2261.

［17］Stuart D. Richard Bellman on the birth of dynamic programming［J］. Operations Research， 2002， 50（1）： 48-51.

［18］庄燕玲， 孙玉姣， 朱涛， 等. 移动货架系统多机器人“存-取货架”调度优化方法［J］. 系统工程理论与实践， 2023，43（2）： 488-508. （Zhuang Yanling， Sun Yujiao， Zhu Tao， et al. Optimization method for multi robot “storage retrieval” scheduling in mobile shelf system［J］. Systems Engineering-Theory & Practice， 2023，43（2）： 488-508.）

［19］Martin A， Martin D， Clemens H， et al. Dual-pivot quicksort： optimality， analysis and zeros of associated lattice paths［J］. Combina-torics Probability and Computing， 2019，28（4）： 485-518.

［20］Civicioglu P. Backtracking search optimization algorithm for numerical optimization problems［J］. Applied Mathematics and Computation， 2013， 219（15）： 8121-8144.

［21］王超， 高扬， 刘超， 等. 基于回溯搜索优化算法求解带时间窗和同时送取货的车辆路径问题［J］. 计算机集成制造系统， 2019， 25（9）： 2237-2247. （Wang Chao， Gao Yang， Liu Chao， et al. Solving vehicle routing problem with time window and simultaneous deli-very and pickup based on backtracking search optimization algorithm［J］. Computer Integrated Manufacturing System， 2019，25（9）： 2237-2247.）

［22］Song Xianhai， Zhang Xueqiang， Zhao Sutao， et al. Backtracking search algorithm for effective and efficient surface wave analysis［J］. Journal of Applied Geophysics， 2015，114： 19-31.

［23］El-Fergany A. Optimal allocation of multitype distributed generators using backtracking search optimization algorithm［J］. International Journal of Electrical Power & Energy Systems， 2015，64（64）： 1197-1205.

［24］Modiri-delshad M， Rahim N A. Solving non-convex economic dispatch problem via backtracking search algorithm［J］. Energy， 2014， 77： 372-381.

［25］董海， 徐晓鹏. 离散回溯搜索算法求解多柔性作业车间调度［J］. 运筹与管理， 2022，31（1）： 87-91. （Dong Hai， Xu Xiaopeng. Discrete backtracking search algorithm for multi flexible job shop scheduling［J］. Operations Research and Management， 2022，31（1）： 87-91.）

［26］胡中波， 王旭鹏. 求解测试用例自动生成问题的多因子回溯搜索优化算法［J］. 计算机应用， 2023， 43（4）： 1214-1219. （Hu Zhongbo， Wang Xupeng. A multifactor backtracking search optimization algorithm for solving the problem of automatic test case generations［J］. Journal of Computer Applications， 2023，43（4）： 1214-1219.）

［27］孙军艳， 陈智瑞， 牛亚儒， 等. 基于嵌套遗传算法的拣货作业联合优化［J］. 计算机应用， 2020，40（12）： 3687-3694. （Sun Junyan， Chen Zhirui， Niu Yaru， et al. Joint optimization of picking operations based on nested genetic algorithm［J］. Journal of Computer Applications， 2020，40（12）： 3687-3694.）