基于虚拟阻抗的模块化直流电源并联均流控制研究
王敬莆
(国网山东省电力公司枣庄供电公司,山东 枣庄 277000)
0 引 言
随着电力电子技术的迅猛发展,直流电源在众多领域中应用广泛。然而,在模块化直流电源并联运行时,由于模块间参数差异、负载变化等导致的均流问题,会影响电源系统的稳定运行。当前,国内外已有多种并联均流控制方法被提出和研究,张豪等人针对谐振元件参数偏差引起的LLC 谐振变换器电流不均衡的问题,将二次侧的同步整流替换成可控整流方式,形成均流控制环路[1];杨玉岗等人为解决并联Boost 变换器全占空比范围内不均流问题,设计一种不对称占空比的均流控制方法,无须增加电流传感器就可以实现并联变换器之间的电流共享[2];董汉菁等人利用混合控制式交错并联LLC 谐振技术,实现LLC 谐振变换器的均流控制,解决了电动汽车充电模块效率低、功率小等问题[3]。但是,这些方法应用于模块化直流电源并联交流控制时效果不尽如人意,所以本次研究旨在深入探究实现基于虚拟阻抗的模块化直流电源并联均流控制方法,为各领域的电力电子设备提供更加可靠的电力保障,为相关领域的发展提供有力支持。
1 检测模块化直流电源并联运行时的环流
环流的存在不仅会降低电源的效率,还会对电源的稳定性和可靠性产生不良影响。因此,进行模块化直流电源并联均流控制至关重要[4]。首先,在模块化直流电源并联运行过程中,检测各并联模块间的电流环流。以两个直流电源模块并联运行为例,假设两个模块的输出电压分别为U1、U2,输出电流分别为I1、I2[5]。在该模块化直流电源的并联运行过程中,产生环流时,并联系统的等效模型为
式中:U'表示模块化直流电源并联系统的负荷电压;R1、R2分别表示两个直流电源模块的线路阻抗;R3表示并联系统的输出阻抗。
同时,定义模块化直流电源并联系统中各模块间的环流为
式中:I0表示模块化直流电源并联系统中的环流理论定义值。
模块化直流电源并联运行时的实际环流,具体计算公式为
式中:I0'表示模块化直流电源并联系统中环流实际检测值。
由式(3)可知,模块化直流电源并联系统中环流的大小主要取决于各模块输出电压的差异和线路阻抗,以此作为后续环流抑制的理论依据。
2 设计虚拟阻抗
在模块化直流电源并联时,通常要求并联系统中电流环流的有效值在负载电流有效值的3%以下,但如果并联的直流电源模块输出的阻抗差异较大,系统电流环流就会超出限值。基于该原理,文章引入虚拟阻抗技术抑制模块化直流电源的并联环流。假设引入虚拟阻抗之后,整个模块化直流电源并联系统的输出阻抗为R(t),则其计算公式为
式中:G(t)表示传递函数;R4(t)表示引入的虚拟阻抗;R5(t)表示模块化直流电源并联控制结构的输出阻抗。
由式(4)可知,在引入虚拟阻抗之后,整个模块化直流电源并联系统的输出阻抗呈增加状态,导致环流对并联系统控制结构的给定电压变化非常敏感,不利于后续环流抑制调节。为了抑制环流的瞬间冲击,文章设计了一种纯阻性虚拟阻抗,通过调整可调电阻的阻值,精确控制虚拟阻抗[9]。在纯阻性虚拟阻抗的设计应用中,已知模块化直流电源并联系统中的虚拟阻抗是一个比例-积分(Proportional-Integral,PI)控制环节,因此可以计算出环流阻抗为
式中:R6(t)表示环流阻抗;μ1表示等效增益;μ2、μ3分别表示两个直流模块电流内环的比例系数;L表示电感;r表示电阻值;t表示时间。
一般来说,模块化直流电源并联系统参考电压的变化值和环流的变化值是一个纯比例关系,根据环流瞬时值即可计算出参考电压需要变化的瞬时值。
3 引入虚拟阻抗抑制并联电源环流
完成纯阻性虚拟阻抗的设计后,即可将该虚拟阻抗引入模块化直流电源并联系统的控制结构,抑制环流。文章在模块化直流电源并联系统的控制结构中引入纯阻性虚拟阻抗,促使给定的输出电压变化值和输出电流瞬时值成正比例。引入虚拟阻抗后的直流电源并联系统控制结构的数学模型为
式中:U0(t)表示模块化直流电源并联系统控制结构的输出电压;U0'(t)表示未引入虚拟阻抗的控制结构的给定电压瞬时值;I3(t)表示模块化直流电源并联系统的负载电流。
为使各直流电源模块之间的输出电流达到均衡状态,需要将各直流电源模块之间的输出环流控制为0。为了让模块化直流电源并联系统环流趋于0,将虚拟阻抗代入环流阻抗的表达式,促使控制结构中的环流阻抗R6(t)调整到足够大的值,此时环流I0'的表达式为
式中:G1(t)表示模块化直流电源并联系统双闭环控制结构的传递函数;G2(t)表示模块化直流电源并联系统的传递函数;G3(t)表示频率到点电压的传递函数;G4(t)表示等效输出电压和实际输出电压之间的传递函数;R7(t)表示模块化直流电源并联系统的阻抗和。
假设各直流电源模块间的参考电压一致,如果设置的环流阻抗足够大,那么模块化直流电源并联系统中各模块之间的容差可以忽略,进而达到输出均流目的,也就是近似得到
式中:In表示并联系统中第n个直流电源模块的输出电流。
总而言之,在直流电源并联系统控制结构中加入虚拟阻抗,可以等效为在并联系统电压控制环路中引入环流反馈。
4 仿真实验
4.1 仿真准备
为了验证设计方法的可行性,利用MATLAB 仿真软件对其进行仿真实验,搭建模块化直流电源并联系统的仿真模型,如图1 所示。
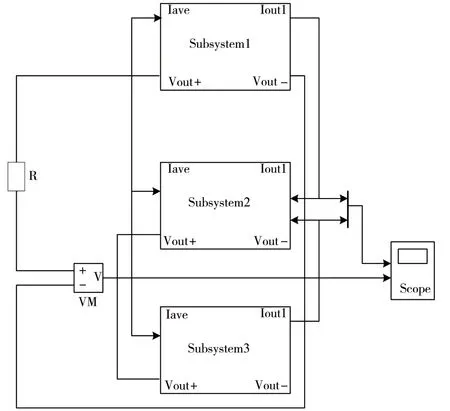
图1 模块化直流电源并联系统仿真模型
由图1 可知,本次实验中搭建了3 个直流电源模块并联的仿真模型。在该仿真模型的直流电源模块空载运行过程中,突加一组2.1 Ω 的电阻负载,此时得到各模块的输出电流仿真波形,如图2 所示。

图2 未采用均流控制的负载电流仿真波形
由图2 可知,未采用均流控制策略时,模块化直流电源并联系统在突加负载后,各模块的负载电流分配不均,模块一承担3.35 A,模块二承担10.82 A,模块三承担16.71 A,导致各模块的输出特性有显著差异。在总负载较大的情况下,这种情况可能导致某个模块过载,而其他模块的容量未被充分利用。因此,该模块化直流电源并联系统需要引入均流控制策略。
4.2 实验结果
以本文设计的基于虚拟阻抗的均流控制方法为实验组,选择基于数字信号处理器(Digital Signal Processor,DSP)的均流控制方法和基于动态稳定控制系统(Dynamic Stability Control,DSC)的均流控制方法为对照组。然后,采用各方法处理并联系统仿真模型中的各直流电源模块的负载电流,所得均流控制后模块化直流电源并联系统的负载电流仿真波形对比如图3 所示。

图3 均流控制后的负载电流仿真波形
图3 显示了3 种均流控制方法下的模块电流分布。其中:DSC 方法下,模块间的最大偏差为3.01 A;DSP 方法下,最大偏差为4.16 A;虚拟阻抗方法下,最大偏差仅为0.58 A。显然,与DSC 和DSP 相比,虚拟阻抗方法在均流效果上表现更佳。这说明,本文研究的基于虚拟阻抗的均流控制方法具有一定的实用价值。
5 结 论
文章引入虚拟阻抗技术设计一种模块化直流电源并联均流控制方法,通过仿真实验的形式验证了该方法具有优越的均流控制效果。虽然文章已经取得一定研究成果,但是仍存在一些不足之处。未来研究工作将致力于解决这些问题,并进一步探究虚拟阻抗与其他控制策略的结合方式,实现更高效、更稳定的模块化直流电源并联均流控制。

