用户负荷不确定下输电网优化规划方法研究
王 惟
(国网江苏省电力有限公司泰州供电分公司,江苏 泰州 225300)
0 引 言
用户负荷是电网运行的基础,其变化直接影响着电网的稳定性和经济性。因此,在用户负荷不确定的条件下,如何进行输电网的优化规划,保证电网的安全、稳定、经济运行,是当前急需解决的问题。传统的输电网规划方法忽略了用户负荷的不确定性,导致规划方案在实际运行中可能面临众多问题。同时,传统方法过于依赖历史数据,而忽略未来负荷的变化和不确定性,在处理复杂的多目标优化问题时,难以找到综合最优解[1]。因此,文章提出用户负荷不确定下的输电网优化规划方法研究。
1 分析用户负荷不确定性
在输电网优化规划中,需要充分考虑用户负荷的不确定性。通过引入Vague 软集理论,从论域与参数集两方面融合不同准则,刻画具有不确定、不精准及不完备特征的用户负荷不确定性因素[2]。Vague 软集利用论域内不确定性元素的真隶属度函数t(x)、伪隶属度函数f(x)及未知信息测度τ(x)来分别表达对用户负荷不确定因素的支持、反对及未知的程度。因此,x对论域D内所有元素的Vague 集构成的集合具有三维信息,即[t(x),f(x),τ(x)],可以简记为[t(x),1-f(x)]。Vague 软集通过区间[t(x),1-f(x)]刻画论域D内各用户负荷不确定集的不确定性程度,其值介于t(x)和1-f(x)之间。设定论域D为非空有限集合,E为用户负荷不确定集,含m个不确定性因素的不确定集合表示为
2 优化输电网结构
针对电网结构优化这一复杂的非线性优化问题,文章提出一种基于节点划分方法和目标级联分析(Analysis Target Cascading,ATC)方法的输电网结构优化(Optimal Transmission Switching,OTS)数学模型。为保持通用性,采用节点撕裂方法,将输电网划分为区域A、B、C 子模块,并对其进行建模[3-4]。
以输电网中传统机组的发电费用最小为目标,建立目标函数为
式中:Cg为单元机组发电总费用;分别为A 区、B 区、C 区单元机组g的发电费用成本函数;分别为A 区、B 区、C 区传统单元机组集合;分别为A 区、B 区、C 区单元机组g的输出功率。
研究输电网约束条件,包括发电机组功率的限制、爬坡限制及节点功率均衡限制。
发电机组功率的限制的公式为
爬坡限制的公式为
节点功率均衡限制的公式为
文章采用短路点自阻抗分析,研究用户负荷不确定下的输电网短路电流超限情况。输电网站点正序等值网络如图1 所示。
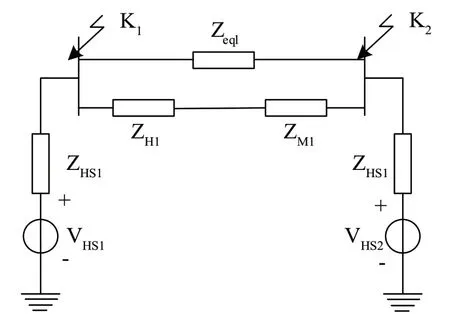
图1 输电网站点正序等值网络
图1 中,ZH1和ZM1为变压器T 型等值电路的正序阻抗,负荷越大,变压器数量越多,其阻抗值就越小;Zeq1是等值的联络阻抗,即220 kV 母线经过500 kV 线再返回220 kV 节点的等值阻抗,随着输电网距离的增加而减小;ZHS1是无电磁输电网的变电站对地的正序阻抗,它反映输电网中各变电站对故障点的传递阻抗,且随着电网联接程度的增加,传递阻抗的幅值逐渐减小;ZMS1表示220 kV 母线到地面的正序阻抗,随着220 kV 母线接入变电站数量的增加,母线的阻抗逐渐减小[5]。短路电流限制措施的主要作用如表1 所示。

表1 限制短路电流措施的主要作用
设计一个上、下两层的系统架构,并将其分解,如图2 所示。

图2 上、下层系统的分解
图2 中:上层系统是A 区,下层系统是B 区、C区;t是一个向量,它是一个由高层系统传送给低层系统的目标矢量;r是由低层系统传递给高层系统的一个响应变量。通过调节上、下层系统的决策数量,使其达到最小,从而优化整个输电网结构。
3 多目标输出输电网规划结果
在目标函数转化为适应度函数的迭代过程中,针对输电网不连通或过负荷情况,分别采用不同的惩罚函数。输电网不连通情况下配置的惩罚函数要远远大于过负荷情况下的惩罚函数,这样的设置旨在使算法在搜索最优解时,能够优先避开输电网不连通和过负荷的情况。只有找到的最优解满足所有约束条件时,算法才会认为该解为有效解,并继续寻找适应度函数在解空间中的全局最优解。这样的设计能够确保算法的有效性和准确性,从而提高输电网优化问题的求解质量[6]。
首先,在解空间中初始化粒子的位置和速度,随机生成输电网架方案,设定输电网架潜在路线数为粒子维数d和所有可能网架方案粒子总数M。其次,在各个粒子形成输电网方案后,惩罚由输电网结构不合理导致的过负荷粒子方案,剔除由输电网网络不连通导致的潮流不收敛粒子方案。再次,对剩余粒子对应的输电网架方案进行潮流计算,并计算该网络的过负荷程度。最后,进行各粒子更新,并按照Tent 混沌映射公式对最优位置Pg=(pg1,pg2,…,pgn)进行映射,将Pgi(i=1,2,…,n)映射到[0,1][7]。在此基础上,利用Tent 方程迭代混沌序列,并将其反演至原始解空间,再进行迭代,从而获得新的混沌序列。直到满足算法预设的最大迭代次数。通过优化输电网规划,可以合理安排电力系统的运行方式和供电计划,从而提高供电的可靠性和稳定性。
4 实 验
为验证文章提出的用户负荷不确定下输电网优化规划方法的有效性,开展对比实验,比较优化方法使用前后输电网供电的可靠性。文章实验参数设置如下:最大负荷为1 000 ~2 000 MW,最小负荷为500 ~800 MW,最大传输容量为2 000 ~3 000 MW,节点数为50 ~100,支路数为100 ~200,目标函数权重系数为0.5 ~1.5,时间步长为6。优化方法使用前后的输电网供电可靠性对比结果如表2 所示。
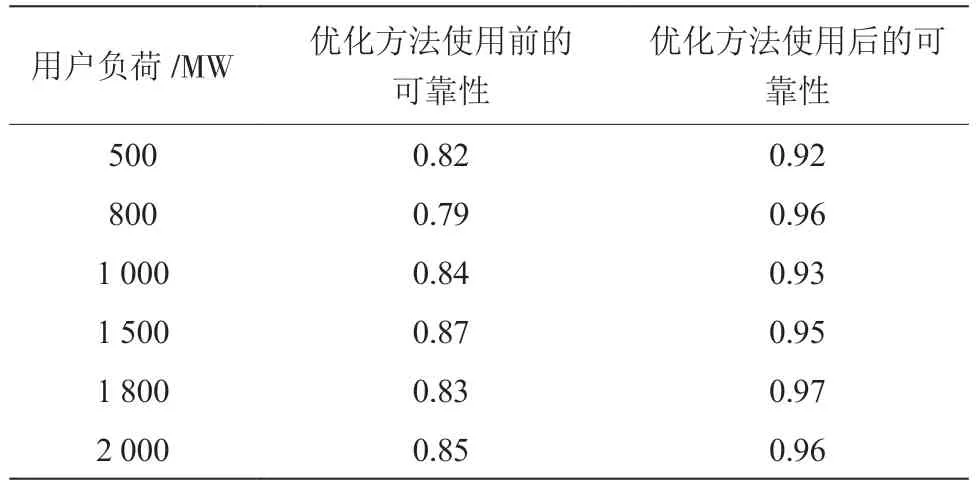
表2 优化方法使用前后的可靠性对比结果
通过表2 可以看出,优化前的输电网供电可靠性范围为0.79 ~0.87,使用文章设计的输电网优化规划方法后,用户负荷对可靠性的影响较少,输电网供电的可靠性都在0.92 以上,有效提高了输电网供电的可靠性。
5 结 论
文章通过深入分析用户负荷的不确定性,制定输电网优化规划方案,增强输电网供电的可靠性。通过明确适应度函数,使用算法来搜索最优解,优化输电网结构。考虑各种目标、约束及解决方案,对多目标进行整合和呈现。实验结果表明,文章设计方法能够有效提高供电可靠性,且输电网优化规划方法更加合理。这一研究为用户负荷不确定下输电网优化规划领域提供重要的参考和指导,具有实际应用价值。

