环境参数对风电齿轮箱传动系统疲劳损伤的影响

伍源 朱才朝 谭建军 宋朝省 张会阳

收稿日期：2022-01-23

网络出版日期：2022-05-07

基金项目：重庆市自然科学基金资助项目（cstc2020jcyj-msxmX0710）；中央高校基本科研业务费资助项目（2020CDJ-LHSS-008，2021CDJCGJ008）。

作者简介：伍源（1997—），男，硕士研究生，主要研究方向为风电机组疲劳损伤分析，（E-mail）2284391610@qq.com。

通信作者：朱才朝，男，教授，博士生导师，（E-mail）cczhu@cqu.edu.cn。

摘要：在风电机组全寿命周期内，长期风速概率分布会使风电齿轮箱传动系统动载荷出现随机特性，影响其疲劳损伤预估精度。笔者提出了一种考虑长期风速概率分布特征的风电齿轮箱传动系统疲劳损伤预估方法，通过建立大功率海上风电机组OpenFAST-SIMPACK联合仿真模型，计算不同平均风速与湍流强度组合工况下的风电齿轮箱传动系统齿轮短期疲劳损伤，进而采用代理模型技术重构“平均风速、湍流强度-短期疲劳损伤”映射关系，预测齿轮长期疲劳损伤。研究结果表明：风电齿轮箱传动系统低速级太阳轮容易发生接触疲劳失效；在额定风速以下，低速级太阳轮短期疲劳损伤与平均风速呈正相关，在额定风速附近，平均风速与湍流强度的随机特性均会增大其长期疲劳损伤不确定性，增大其疲劳失效风险。

关键词：风电齿轮箱；传动系统；疲劳损伤；随机特性

中图分类号：TH113          文獻标志码：A           文章编号：1000-582X（2024）03-132-13

大功率海上风电机组是目前最有效地开发海上风能资源的重大海洋工程装备之一。风电齿轮箱是风电机组中传递力与运动的关键传动装置。据统计，海上风电齿轮箱故障率比陆上高5%以上^[1]。这是由于海面粗糙度比陆地小，海表风速大、季节性变化明显，因而由风剪切效应造成的作用在风电齿轮箱的气动载荷波动幅值大、随机性强，造成海上风电齿轮箱疲劳失效间隔时间短^[2]。同时，海上风电装备运维成本比陆上高10%以上^[1]，对海上风电齿轮箱可靠性设计提出了更高要求。因此，开展考虑长期风速概率分布特征的风电齿轮箱传动系统疲劳损伤随机特性分析对指导海上风电齿轮箱设计、提高其可靠性具有重要意义。

近年来，国内外学者对风电齿轮箱传动系统疲劳损伤开展了大量研究。Dong等^[3]分别建立风电机组整机动力学模型和齿轮箱动力学模型，利用解耦方法计算了不同风速作用下风电机组全局气动载荷，分析了不同气动载荷作用下风电齿轮箱传动系统齿轮接触应力概率分布特征；向东等^[4]建立随机风载作用下风电齿轮箱传动系统短期疲劳损伤计算模型，分析了随机风速下各齿轮的短期弯曲疲劳与接触疲劳损伤；Nejad等^[5-7]针对风电齿轮箱传动系统疲劳损伤分析开展了大量研究，包括考虑长期风速概率分布的10 MW与5 MW风电齿轮箱传动系统齿轮长期疲劳损伤计算模型、考虑随机波浪作用下4种浮式平台对风电齿轮箱传动系统长期疲劳损伤影响等；熊中杰^[8]建立考虑时变啮合刚度和阻尼的齿轮箱动力学模型，分析不同风速、不同载荷类型下的风电齿轮箱疲劳损伤规律。文献[3-8]报道了有效预测风电齿轮箱传动系统长期疲劳损伤的方法，通过等间距离散平均风速，计算各风速工况下的齿轮短期疲劳损伤后加权求和得到长期疲劳损伤，但离散间距取值主要依靠设计者经验，离散后所需仿真的环境参数组合工况数量多，计算耗时。

为了提高传动系统长期疲劳损伤的计算效率，部分学者将多项式响应面（polynomial response surface，PRS）、克里金（kriging，KRG）、人工神经网络（artificial neural network，ANN）和径向基函数（radial basis function，RBF）等代理模型方法引入到复杂系统动力学分析中^[9-12]。Juan等^[13]建立了环境参数与风电机组等效疲劳载荷和发电量之间的PRS代理模型，并开展环境参数全局灵敏度分析；Li等^[14]考虑风浪等环境工况相关性，利用KRG代理模型预测漂浮式风电机组系泊缆、塔架底座和顶部横截面的长期疲劳损伤；Zhang等^[15]利用ANN和KRG等代理模型计算动态环境载荷下浮式风电机组系泊线的疲劳失效概率；Wilkie等^[16]利用高斯过程回归代理模型预测了海上风电机组疲劳损伤、疲劳可靠性等性能，分析风和波浪等环境参数对性能指标的影响。文献[13-16]报道了高效的风电机组疲劳损伤分析的计算方法，但忽略了平均风速与湍流强度概率分布对风电齿轮箱传动系统疲劳损伤随机特性的影响。

笔者考虑随机风速与风电机组拓扑结构，建立大功率海上风电机组OpenFAST-SIMPACK联合仿真模型；考虑长期风速概率分布特征，利用Copula函数构建平均风速-湍流强度联合概率分布，建立平均风速-湍流强度关键工况集合，计算对应的风电齿轮箱传动系统齿轮短期疲劳损伤；采用代理模型技术重构“平均风速、湍流强度-疲劳损伤”映射关系，预测齿轮长期疲劳损伤。

1海上风电机组OpenFAST-SIMPACK联合仿真建模

1.1风电机组结构及运行原理

图1所示为某型风电机组齿轮箱传动系统结构及原理。海上风电机组主要由风轮、主轴、齿轮箱、发电机、塔筒及塔架等组成。在随机风速作用下，叶片将风能转变为机械能，并通过主轴驱动齿轮箱转动。齿轮箱主要包括低速级、中间级和高速级三级传动结构，其中低速级和中间级为行星斜齿轮传动，高速级为平行轴斜齿轮传动。发电机通过联轴器与高速轴相连。海上风电机组基本设计参数如表1所示，风电齿轮箱主要设计参数如表2所示。

1.2OpenFAST-SIMPACK联合仿真模型

图2所示为大功率海上风电机组OpenFAST-SIMPACK联合仿真模型，主要包括2类不同层级的子模型，即风电机组整机全局耦合模型与风电齿轮箱传动系统动力学模型。首先，利用OpenFAST^[17]建立大功率海上风电机组整机全局耦合模型，控制策略采用变速-变桨控制^[18]；为了提高计算效率，风电齿轮箱传动系统简化为传动比。然后，利用SIMPACK^[19]建立风电齿轮箱传动系统动力学模型，其中齿轮副采用切片理论建模、传动轴与行星架简化为刚体，轴承利用6×6刚度矩阵模拟；发电机和联轴器采用集中质量单元建模^[20]。

为了实现OpenFAST-SIMPACK联合仿真，利用Matlab动态修改OpenFAST风电机组整机全局耦合模型工况.inp文件，计算任意给定平均风速-湍流强度环境参数下的风电机组轮毂处6自由度气动载荷；利用Matlab将气动载荷文件格式转为SIMPACK风电齿轮箱传动系统动力学模型载荷.afs文件，并同时调用其宏命令.sjs文件进行仿真，计算风电齿轮箱传动系统齿轮副动态啮合力。

2考虑长期风速分布的风电齿轮箱传动系统疲劳损伤预估

2.1长期风速概率分布

根据IEC61400-1标准^[21]，将10 min时序风速的平均值作为平均风速，其概率密度函数通常服从威布尔分布

2.2关键环境工况

为了从中高效地抽选权重占比较高的平均风速-湍流强度环境参数组合工况，结合拉丁超立方抽样法^[27]与最大差异法^[28]两者优点，建立图3所示关键环境工况分析流程，以保证在抽样样本数量较少的条件下，同时保持各抽样维度均匀性与差异最大性，具体步骤如下。

2.3齿轮长期疲劳损伤

3结果讨论与分析

根据中国某海上风电场历年风速统计数据，建立平均风速-湍流强度联合概率密度函数，并选取关键环境工况，分别计算各关键环境工况下风电齿轮箱传动系统齿轮副动态啮合力（各工况仿真时间100 s），并计算齿轮短期和长期疲劳损伤；最后分析环境参数对齿轮短期和长期疲劳损伤的影响规律。

3.1环境参数对风电齿轮箱传动系统齿轮短期疲劳损伤影响

图6与图7分别为平均风速概率密度函数和湍流强度概率密度函数，其中平均风速威布尔分布函数为，湍流强度伽马分布函数为。

图8所示为平均风速与湍流强度之间的相关性。从图中可以看出，平均风速与湍流强度彼此之间存在明显的“上尾相关性”，符合Gumbel Copula函数特征，因此，根据式（3）和（4）可得平均风速-湍流强度联合概率密度函数，如图9所示。

图10所示为平均风速、湍流强度分别对低速级太阳轮接触与弯曲应力均值与方差的影响。从图10（a）中可以看出，当平均风速低于额定风速时，低速级太阳轮接触与弯曲应力均值随平均风速增加而增大；當平均风速高于额定风速时，接触与弯曲应力均值基本稳定；低速级太阳轮接触应力均值远大于弯曲应力均值。从图10（b）中可以看出，接触应力方差在10～40 MPa波动，弯曲应力方差在0～25 MPa波动，总体上，低速级太阳轮接触应力方差大于弯曲应力方差。

图11所示为在额定风速（平均风速9.58 m/s，湍流强度0.11）作用下风电齿轮箱传动系统各级齿轮短期接触与弯曲疲劳损伤。可以看出，低速级太阳轮的短期接触疲劳损伤最大，同时各级齿轮短期接触疲劳损伤均大于弯曲疲劳损伤。

图12所示为平均风速、湍流强度对低速级太阳轮短期接触与弯曲疲劳损伤的影响。从图12（a）中可知，当平均风速低于额定风速时，低速级太阳轮短期接触与弯曲疲劳损伤随平均风速增加而增大；当平均风速高于额定风速时，平均风速对其影响较小。其主要原因是当风速低于额定风速时，风电机组以追踪最佳风能利用系数运行，载荷变化明显；当风速高于额定风速时，由于变桨系统限制了风电机组功率超发，载荷较为稳定。从图12（b）中可以看出，当平均风速低于8.0 m/s时，低速级太阳轮短期接触与弯曲疲劳损伤主要受平均风速影响，湍流强度影响较小；当平均风速在8.0～9.5 m/s时，其损伤会随着湍流强度的增加而增大；当平均风速高于9.5 m/s时，由于控制策略作用，湍流强度对其损伤影响较小。

3.2环境参数对风电齿轮箱传动系统齿轮长期疲劳损伤影响

为了验证本文方法计算结果的精度与效率，将本文方法与常规方法计算的齿轮长期疲劳损伤进行对比分析，如式（15）所示。在常规计算方法中，在平均风速3～25 m/s、湍流强度0～0.25的区间内，以平均风速间隔0.75 m/s、湍流强度间隔0.05选取115个环境参数组合工况，直接根据概率累加计算风电齿轮箱传动系统齿轮长期疲劳损伤。

图13所示为本文方法与常规方法计算的风电齿轮箱传动系统齿轮长期疲劳损伤计算结果与误差对比。从图中可以看出，本文方法与常规方法计算的结果误差小于8%。整个仿真分析在一台CPU型号为i7-4790K，主频为4.00 GHz的台式计算机上完成，其中常规方法计算耗时约72 h，而本文方法计算仅耗时约20 h，效率提高260%。

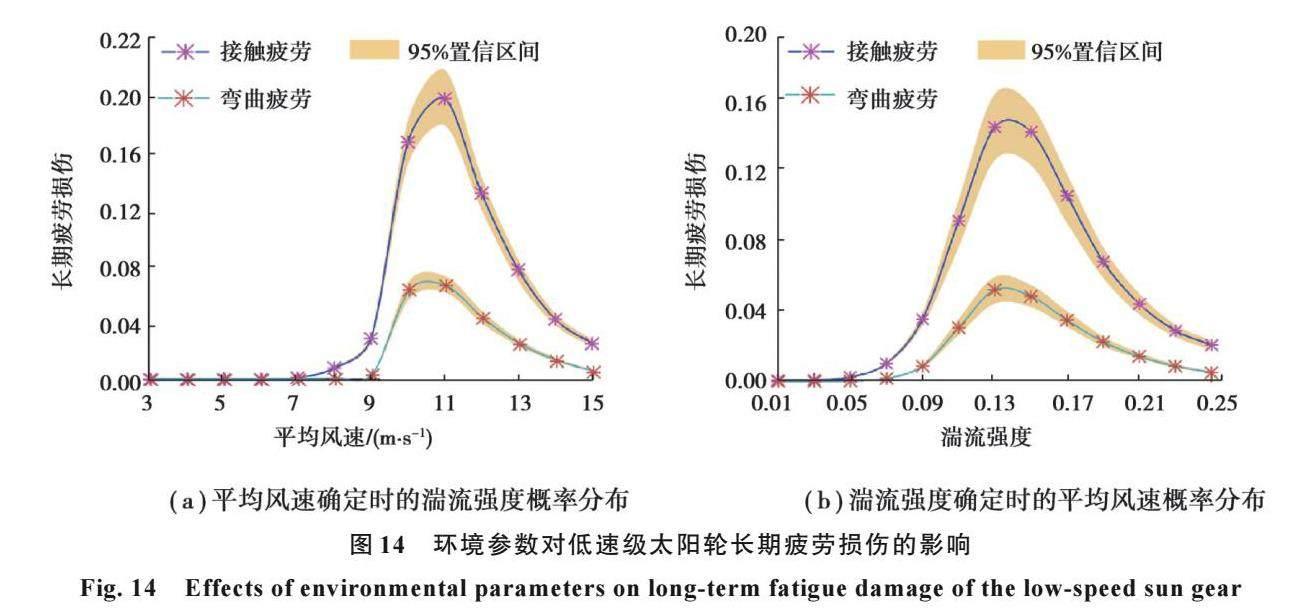
图14所示为平均风速、湍流强度对低速级太阳轮长期接触与弯曲疲劳损伤随机特性的影响。其中，黄色阴影部分表示当平均风速确定，湍流强度概率分布如图14（a）时，或当湍流强度确定，平均风速概率分布如图14（b）时，95%置信区间内的齿轮长期疲劳损伤。从图14（a）中可以看出，低速级太阳轮长期接触与弯曲疲劳损伤随着平均风速的增加而先增后减，同时由于湍流强度的随机性，尤其当平均风速位于10～11 m/s时齿轮长期疲劳损伤出现明显的随机不确定性。从图14（b）中可以看出，低速级太阳轮长期接触与弯曲疲劳损伤随湍流强度的增加也呈现出先增后减的趋势；当湍流强度在0.14附近时齿轮长期疲劳损伤最大，同时其随机不确定性也越明显，疲劳失效风险增大。

4结  论

笔者考虑长期风速概率分布特征，建立了大功率海上风电机组OpenFAST-SIMPACK联合仿真模型，通过关键环境工况分析，计算对应的风电齿轮箱传动系统齿轮短期疲劳损伤，基于代理模型预测齿轮长期疲劳损伤，得出结论如下：

1） 通过关键环境工况选取与基于代理模型的风电齿轮箱传动系统齿轮长期疲劳损伤计算，相对于常规方法，其计算效率可以提高260%，且误差小于8%。

2） 风电齿轮箱传动系统各级齿轮接触疲劳损伤均高于弯曲疲劳损伤，其中低速级太阳轮接触疲劳损伤最大，易发生疲劳失效。

3） 在额定风速以下时，低速级太阳轮短期疲劳损伤与平均风速呈正相关，而在额定风速附近时，其主要受湍流强度影响；平均风速与湍流强度的随机特性会增大低速级太阳轮长期疲劳损伤不确定性。

参考文献

［1］  李垚， 朱才朝， 陶友传， 等. 风电机组可靠性研究现状与发展趋势[J]. 中国机械工程， 2017， 28（9）： 1125-1133.

Li Y， Zhu C C， Tao Y C， et al. Research status and development tendency of wind turbine reliability[J]. China Mechanical Engineering， 2017， 28（9）： 1125-1133. （in Chinese）

［2］  王磊. 海上风电机组系统动力学建模及仿真分析研究[D]. 重庆： 重庆大学， 2011.

Wang L. Study on systematic dynamic model and simulation for offshore wind turbine[D]. Chongqing： Chongqing University， 2011. （in Chinese）

［3］  Dong W B， Xing Y H， Moan T， et al. Time domain-based gear contact fatigue analysis of a wind turbine drivetrain under dynamic conditions[J]. International Journal of Fatigue， 2013， 48： 133-146.

［4］  向东， 蒋李， 沈银华， 等. 风电齿轮箱在随机风载下的疲劳损伤计算模型[J]. 振动与冲击， 2018， 37（11）： 115-123.

Xiang D， Jiang L， Shen Y H， et al. Fatigue damage calculation model for wind turbine gearboxes under random wind loads[J]. Journal of Vibration and Shock， 2018， 37（11）： 115-123. （in Chinese）

［5］  Nejad A R， Gao Z， Moan T. On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains[J]. International Journal of Fatigue， 2014， 61： 116-128.

［6］  Nejad A R， Bachynski E E， Kvittem M I， et al. Stochastic dynamic load effect and fatigue damage analysis of drivetrains in land-based and TLP， spar and semi-submersible floating wind turbines[J]. Marine Structures， 2015， 42： 137-153.

［7］  Wang S S， Nejad A R， Moan T. On design， modelling， and analysis of a 10-MW medium-speed drivetrain for offshore wind turbines[J]. Wind Energy， 2020， 23（4）： 1099-1117.

［8］  熊中杰. 隨机风速下风力发电机组齿轮箱疲劳断裂寿命研究[D]. 南京： 南京理工大学， 2019.

Xiong Z J. Research on fatigue fracture life of wind turbine gearbox under random wind[D]. Nanjing： Nanjing University of Science and Technology， 2019. （in Chinese）

［9］  Heidebrecht A， MacManus D G. Surrogate model of complex non-linear data for preliminary nacelle design[J]. Aerospace Science and Technology， 2019， 84： 399-411.

［10］  Palmer K， Realff M. Metamodeling approach to optimization of steady-state flowsheet simulations： model generation[J]. Chemical Engineering Research and Design， 2002， 80（7）： 760-772.

［11］  Jia Z Y， Davis E， Muzzio F J， et al. Predictive modeling for pharmaceutical processes using kriging and response surface[J]. Journal of Pharmaceutical Innovation， 2009， 4（4）： 174-186.

［12］  Milovanovi? S， von Sydow L. A high order method for pricing of financial derivatives using radial basis function generated finite differences[J]. Mathematics and Computers in Simulation， 2020， 174： 205-217.

［13］  Murcia J P， Réthoré P E， Dimitrov N， et al. Uncertainty propagation through an aeroelastic wind turbine model using polynomial surrogates[J]. Renewable Energy， 2018， 119： 910-922.

［14］  Li X A， Zhang W. Probabilistic fatigue evaluation of floating wind turbine using combination of surrogate model and copula model[C]//Proceedings of the AIAA Scitech 2019 Forum， San Diego， California. Reston， Virginia： AIAA， 2019： AIAA2019-0247.

［15］  Zhao Y L， Dong S. Probabilistic fatigue surrogate model of bimodal tension process for a semi-submersible platform[J]. Ocean Engineering， 2021， 220： 108501.

［16］  Wilkie D， Galasso C. Impact of climate-change scenarios on offshore wind turbine structural performance[J]. Renewable and Sustainable Energy Reviews， 2020， 134： 110323.

［17］  Jonkman B， Jonkman J. FAST v8. 16.00 a-bjj[EB/OL]. 2016-07-16[2021-12-20]. https：//openfast.readthedocs.io/en/v3.5.2/_downloads/5f2ddf006568adc9b88d8118dc3f1732/FAST8_README.pdf.

［18］  陳旭， 朱才朝， 宋朝省， 等. 紧急停机工况下风力发电机系统动态特性分析[J]. 机械工程学报， 2019， 55（5）： 82-88.

Chen X， Zhu C C， Song C S， et al. Dynamic characteristics analysis of wind turbine under emergency shutdown events[J]. Journal of Mechanical Engineering， 2019， 55（5）： 82-88. （in Chinese）

［19］  陈岩松， 朱才朝， 谭建军， 等. 多工况下兆瓦级海上风电齿轮箱均载性能优化设计[J]. 重庆大学学报， 2022， 45（09）： 1-14.

Chen Y S， Zhu C C， Tan J J， et al. Optimal design of load sharing performance of megawatt level offshore wind turbine gearbox under multi-operating conditions[J]. Journal of Chongqing University， 2022， 45（09）： 1-14.（in Chinese）

［20］  刘华朝， 朱才朝， 柏厚义. 轮齿修形对兆瓦级风电齿轮箱NVH性能的影响[J]. 振动与冲击， 2016， 35（24）： 158-163， 188.

Liu H C， Zhu C C， Bai H Y. The effect of gear modification on the NVH characteristics of a megawatt level wind turbine gearbox[J]. Journal of Vibration and Shock， 2016， 35（24）： 158-163， 188. （in Chinese）

［21］  International Electrotechnical Commission. Wind turbines - Part 1： design requirements ： IEC 61400-1：2005 [S]. IEC， 2006.

［22］  Li H X， Cho H， Sugiyama H， et al. Reliability-based design optimization of wind turbine drivetrain with integrated multibody gear dynamics simulation considering wind load uncertainty[J]. Structural and Multidisciplinary Optimization， 2017， 56（1）： 183-201.

［23］  龚伟俊， 李为相， 张广明. 基于威布尔分布的风速概率分布参数估计方法[J]. 可再生能源， 2011， 29（6）： 20-23.

Gong W J， Li W X， Zhang G M. The estimation algorithm on the probabilistic distribution parameters of wind speed based on Weibull distribution[J]. Renewable Energy Resources， 2011， 29（6）： 20-23. （in Chinese）

［24］  Sklar A. Fonctions de repartition an dimensions et leurs marges[J]. Publ. inst. statist. univ. Paris， 1959， 8： 229-231.

［25］  涂志斌， 黄铭枫， 楼文娟， 等. 基于Copula函数的风浪多方向极限状态曲线[J]. 振动与冲击， 2021， 40（14）： 1-9， 46.

Tu Z B， Huang M F， Lou W J， et al. Dimensional environmental contour lines of the wind and wave based on Copula functions[J]. Journal of Vibration and Shock， 2021， 40（14）： 1-9， 46. （in Chinese）

［26］  侯亚楠. Copula函数的估计及其应用[D]. 武汉： 华中科技大学， 2013.

Hou Y N. The estimation and application of copula function[D]. Wuhan： Huazhong University of Science and Technology， 2013. （in Chinese）

［27］  Khowaja K， Shcherbatyy M， H?rdle W K. Surrogate models for optimization of dynamical systems[EB/OL]. 2021： arXiv： 2101.10189. https：//arxiv.org/abs/2101.10189.pdf.

［28］  Martini M， Guanche R， Armesto J A， et al. Met-ocean conditions influence on floating offshore wind farms power production[J]. Wind Energy， 2016， 19（3）： 399-420.

［29］  周金宇， 谢里阳， 韩文钦， 等. 基于Nataf变换的载荷相关系统风险预测方法[J]. 机械工程学报， 2009， 45（8）： 137-141.

Zhou J Y， Xie L Y， Han W Q，et al. Method for syetem risk prediction with load dependency based on nataf transformation[J]. Journal of Mechanical Engineering， 2009， 45（8）： 137-141. （in Chinese）

［30］  張立波， 程浩忠， 曾平良， 等. 基于Nataf逆变换的概率潮流三点估计法[J]. 电工技术学报， 2016， 31（6）： 187-194.

Zhang L B， Cheng H Z， Zeng P L， et al. A three-point estimate method for solving probabilistic load flow based on inverse Nataf transformation[J]. Transactions of China Electrotechnical Society， 2016， 31（6）： 187-194. （in Chinese）

［31］  International Organization for Standardization. Calculation of load capacity of spur and helical gears - Part 6： calculation of service life under variable load： ISO 6336-6：2006 [S]. Switzerland： International Organization for Standardization， 2006．

［32］  International Organization for Standardization. Calculation of load capacity of spur and helical gears - Part 2： calculation of surface durability （pitting）： ISO 6336-2：2006 [S]. Switzerland： International Organization for Standardization， 2006．

［33］  International Organization for Standardization. Calculation of load capacity of spur and helical gears - Part 3： calculation of tooth bending strength： ISO 6336-3：2006 [S]. Switzerland： International Organization for Standardization， 2006.

［34］  Miner M A. Cumulative damage in fatigue[J]. Journal of Applied Mechanics， 1945， 12（3）： A159-A164.

［35］  International Organization for Standardization. Calculation of load capacity of spur and helical gears - Part 5： strength and quality of materials： ISO 6336-5：2003 [S]. Switzerland： International Organization for Standardization， 2003．

［36］  龍腾， 刘建， Wang G G， 等. 基于计算试验设计与代理模型的飞行器近似优化策略探讨[J]. 机械工程学报， 2016， 52（14）： 79-105.

Long T， Liu J， Wang G G， et al. Discuss on approximate optimization strategies using design of computer experiments and metamodels for flight vehicle design[J]. Journal of Mechanical Engineering， 2016， 52（14）： 79-105. （in Chinese）

［37］  Okpokparoro S， Sriramula S. Uncertainty modeling in reliability analysis of floating wind turbine support structures[J]. Renewable Energy， 2021， 165： 88-108.

［38］  Rashki M， Azarkish H， Rostamian M， et al. Classification correction of polynomial response surface methods for accurate reliability estimation[J]. Structural Safety， 2019， 81： 101869.

［39］  Wang H， Li W B， Qian Z H， et al. Reconstruction of wind pressure fields on cooling towers by radial basis function and comparisons with other methods[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2021， 208： 104450.

［40］  Bhosekar A， Ierapetritou M. Advances in surrogate based modeling， feasibility analysis， and optimization： a review[J]. Computers & Chemical Engineering， 2018， 108： 250-267.

（编辑  吕建斌）