锚杆-围岩结构的耦合振动和减振

李苗苗 王卫 李英民

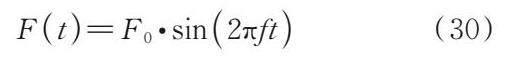
DOI： 10.11835/j.issn.2096-6717.2021.255

收稿日期：2021?09?03

基金项目：国家自然科学基金（51638002）

作者简介：李苗苗（1996- ），女，主要從事防灾减灾工程与防护工程研究，E-mail：1531146239@qq.com。

通信作者：李英民（通信作者），男，教授，博士生导师，E-mail：liyingmin@cqu.edu.cn。

Received： 2021?09?03

Foundation item： National Natural Science Foundaton of China （No. 51638002）

Author brief： LI Miaomiao （1996- ）， main research interests： disaster prevention and reduction engineering and protective engineering， E-mail： 1531146239@qq.com.

corresponding author：LI Yingmin （corresponding author）， professor， doctorial supervisor， E-mail： liyingmin@cqu.edu.cn.

摘要：锚杆支护是隧道施工中常见的支护手段，而随着施工工况日趋复杂，锚杆与围岩的组合结构也承受着各类动力荷载的影响。针对隧道中单根锚杆的受力特性有较多研究，而对于锚杆和围岩组合体的动力特性研究较少。对锚杆-围岩结构进行整体分析，简化出一种巷道顶板锚杆支护模型，结合动力学双梁理论，建立并求解出模型动力学方程；运用MATLAB软件进行数值模拟，研究不同支护参数下结构的自振特性以及在外荷载作用下的动力响应，提出减振措施；利用有限元软件GTS NX建立二维模型，验证支护体系的安全性。结果表明：锚杆-围岩结构的动力特性与锚固段长度、锚杆间距和锚杆直径有关。在所建模型中，随着锚固段长度与锚杆间距的适当增加，结构动力响应明显减弱；随着锚杆直径的变化，结构动力特性的变化情况较复杂，结构不同部位的动力响应变化趋势差别较大。

关键词：锚杆支护；围岩振动；减振措施；双梁结构

中图分类号：U455.7     文献标志码：A     文章编号：2096-6717（2024）02-0051-09

Coupling vibration and vibration reduction of anchor-surrounding rock structure

LI Miaomiao¹， WANG Wei²， LI Yingmin¹

（1. School of Civil Engineering， Chongqing University， Chongqing 400045， P. R. China； 2. China State Construction Engineering Co.， Ltd.， Beijing 100037， P. R. China）

Abstract： Bolt support is a common means in tunnel construction， and with the increasing working condition complexity， the combined structure of bolt and surrounding rock is also subjected to various dynamic loadings.  In the past， researches focused on the mechanical characteristics of single bolt in tunnel， but there are few on the dynamic characteristics of the combination of bolt and surrounding rock. In this paper， the overall analysis of the bolt-surrounding rock structure， with a simplified roadway roof bolt-supporting model， combined with the dynamic double beam theory， was established to solve the dynamic model equation; MATLAB was used for numerical simulation to study the natural vibration characteristics of the structure under different supporting parameters and the dynamic response under the external load， and the vibration reduction measures were proposed. Finally， GTS NX is used to verify the safety of the supporting system. The results show that the dynamic characteristics of rock bolt-surrounding rock structure are related to the length of anchor segment， the distance between bolts and the diameter of bolts. In the model established in this paper， the dynamic response of the structure decreases obviously with the proper increase of anchorage length and bolt spacing. With change of bolt diameter， the dynamic characteristics of the structure are becoming complicated， and the dynamic response of different parts of the structure varies greatly.

Keywords： bolt support； vibration of surrounding rocks； vibration reduction measures； double-beam structure

隧道与地下煤矿常常面临着支护问题，如何保证结构不垮塌，如何保证围岩的稳定性是这些建筑工程需要重点考虑的问题。

康红普^[1]总结了新中国成立70年来中国煤矿巷道围岩控制领域取得的主要研究成果，重点介绍了预应力锚杆支护理论及支护应力场的概念；康红普等^[2-3]采用理论计算、数值模拟及室内试验等方法，研究了锚杆形状、参数对其锚固力、安装阻力的影响以及钢筋、尾部螺纹、托板材料与几何参数对锚杆构件的力学性能的影响；王爱文等^[4]在传统锚杆的基础上增加吸能装置，通过解析方法研究得到锚杆端部位移阻抗函数的表达式，并发现增加吸能装置的支护系统在冲击荷载作用下的稳定性得到较大提高；胡帅伟等^[5]采用结构动力学理论，推导出锚杆在爆破地震波作用下的振动规律，研究了黏结式锚杆在爆破动荷载作用下的动力响应特征；吉凌等^[6]借助数值模拟与现场测试方法，揭示了隧道开挖爆破作用下围岩的振动响应特征，基于此特征进一步研究隧道爆破作用下不同位置沿开挖轴线方向损伤范围的分布，并提出围岩爆破振动速度控制值；李壮等^[7]采用分离式霍普金森压杆试验研究了不同预紧力作用下锚固体的冲击破坏响应，获得了锚固体的动态应力-应变曲线，分析了预紧力对锚固体动载变形与强度特征的影响，以及冲击破坏过程中裂纹扩展与锚杆动态应变演化特征；He等^[8]发明了一种恒阻大变形锚杆，可更好地控制深部巷道的大变形；Spearing等^[9]介绍了一种现场测试锚杆各项参数的技术；Zhang等^[10]运用现场监测和数值模拟的方法研究了长壁工作面开采期间锚杆的应力变化，并对其设计进行了改进；刘海雁等^[11]采用正交数值模拟方法，系统研究不同锚杆长度、预紧力及顶角锚杆安装角度下的塑性区体积、顶底板移近量和两帮收敛量的变化规律，為巷道锚杆支护设计和优化提供了新的视角；张明磊等^[12]将模糊数学和可拓学相结合，对巷道支护参数进行了优化设计；赵东平等^[13]对近40年公开发表的隧道锚杆研究论文进行统计和分析发现，既有研究大多聚焦于锚杆的受力特性以及单根锚杆的理论计算问题，关于系统锚杆力学机理及系统锚杆与围岩形成的复合承载拱承载机理仅有少量研究。

综上所述，锚杆支护已成为巷道围岩控制的主体方式，解决了一般条件下的巷道支护问题。但目前关于隧道锚杆研究尚不充分，大多聚焦于锚杆的受力特性以及单根锚杆的理论计算问题，研究成果明显偏少，且尚未形成统一认识。特别是在锚杆的设计参数方面，研究采用的主要方法是经验类比法，精细定量的设计方法和合理有效的优化方法成为巷道支护的研究热点。笔者基于隧洞中客观存在的松动圈现象，考虑中松动圈下的悬吊机理，采用结构力学模式的核心观点，即结构-荷载观点，抽象出锚杆-围岩整体结构的力学模型，结合结构动力学中的双梁理论，研究耦合振动作用，系统分析不同支护参数对围岩振动的影响，探究降低围岩动力反应的关键参数，并尝试给出减振优化措施。

1 锚杆-围岩结构耦合振动模型的建立及求解

1.1 建立模型

考虑岩土体、地应力的复杂性，采用以下简化假设：1）分析对象针对隧洞顶板；2）使用过程中锚杆不出现断裂失效、拔出失效；3）上方岩梁横截面高度受锚固段长度控制。

隧洞基本条件假设为：Ⅲ级围岩，开挖跨度B=15m，埋深15 m，考虑厚度为100 cm的中松动圈，见图1（a）。分析采用的模型如图1（b）所示：将锚杆-围岩结构看作由上部两端固定的梁和下部两端自由的梁，通过弹簧（锚杆）连接而成的一种双梁模型。

需要指出的是，隧道开挖后，围岩自身具备一定的强度和承载能力，而在模型简化中仅把松动圈范围内的围岩视作荷载，同时未考虑周边围压对隧道顶板松动圈范围内的岩土体产生的约束作用，认为锚杆起悬吊作用，支护松动圈范围内的围岩。故模型是一种不利工况的考虑，在工程上相对安全保守。

1.2 锚杆-围岩结构模型的参数优化

求解上述模型的耦合振动，需要用到的参数为：梁间锚杆的分布刚度、上下部岩梁的弹性模量和惯性矩、密度、横截面积等。

1）分布刚度

采用文献[14]所介绍的方法计算锚杆刚度。

将锚杆刚度分布在跨度范围内，得到双梁间锚杆的分布刚度

式中：k_T为岩石锚杆的刚度；L_a为锚固长度；L_f为自由段长度；β为锚杆与竖直方向的夹角；S为开挖跨度；d为锚杆布置间距。

2）弹性模量E

目前中国围岩分级方法主要采用BQ国标法，而国际上对围岩分级比较通行的是RMR系统。有不少学者对两种体系指标的换算给出了研究分析。其中邬爱清等^[15]基于200多组实测数据，通过回归分析建立了BQ与RMR之间的关系式

许宏发等^[16]根据内摩擦角和变形模量的等效原则，通过比较RMR和BQ对内摩擦角和变形模量的表达，给出RMR和BQ之间的关系式

取Ⅲ级围岩对应的BQ=400，带入式（4）和式（5），分别得到RMR=52.38和RMR=51.60，取二者平均值RMR=52。

根据Serafim等^[17]的研究，当RMR值小于等于55时，相应岩体的弹性模量取为

带入数据，得Ⅲ级围岩岩体的弹性模量为E₁=11 220.2 MPa。

开挖过程中的扰动会引起岩体中原生结构面以及微隐裂痕的张开和错动，使得开挖后松动圈岩体的弹性模量E₂＜E₁。参考有关实测数据，在吉图珲客运专线的小盘岭2号隧道中，与岩体最大弹性模量（岩块弹性模量）相比，开挖后围岩软弱方向的弹性模量仅为最大弹性模量的29.3%^[18]。故取下方岩梁的弹性E₂=0.5E₁=5 610.1 MPa 。

3）惯性矩I

计算惯性矩时，下方岩梁的横截面高度取松动圈厚度100 cm。

一定能级的波仅对一定范围内的岩体产生作用，即耦合振动并不会对隧洞顶板上方全部岩体产生影响，所以上方岩梁惯性矩的计算涉及耦合振动影响范围的确定。目前与本文相似的研究方向较少，对于锚杆-围岩的耦合振动影响范围没有可直接参考的研究。但注意到锚固段注浆体的受力特点为：在锚固段与自由段连接处剪切应力最大，沿锚固段方向迅速衰减，在锚固段注浆体后半段接近于零。考虑振动时注浆体后半段也会受力，即锚杆带动整个注浆段开始振动。于是假定上部岩梁横截面高度由锚固段长度决定，其惯性矩可表示为

1.3 锚杆-围岩结构耦合振动模型求解

从能量角度出发，借鉴双梁结构振动问题的求解方法，求解出锚杆-围岩组合结构的自振频率、振型、受迫振动等动力特性的解。

任意边界条件下无阻尼系统双梁结构的自由振动模型如图2所示。

考虑到梁间通过弹性层的耦合作用，双梁的运动方程为

式中：ω_n为双梁结构的第n阶自振频率；Α_nj、Β_nj、D_n、P_nj、β_nj為与第n阶自振频率有关的未知常数。将式（21）带入式（13）定义的实际边界条件中，可得到8个代数方程，其矩阵形式可表示为

式中：为未知常数矩阵；[E]_8×8是与边界条件有关的系数矩阵。

若使式（22）有非零解，则要求系数矩阵行列式等于零，也即|E|=0。此处利用半解析的方法和切割法可求得常数ω、Α、Β、P、β的值。边界条件系数矩阵[E]_8×8与结构的实际支承状态有关。模型为上梁两端固支、下梁两端自由，其对应的矩阵[E]_8×8如式（23）所示。

此外，自由振动中的参数D可通过能量平衡方程和振型正交条件求出。

最终，双梁结构自由振动时，求得上下梁振动的解为

在此基础上，进行双梁结构受迫振动问题的求解。受迫振动的求解与自由振动类似，设受迫振动情况下双梁结构的特解为

式中：分别是与n阶自振频率有关的上下梁振型函数，通过自由振动求解已知。T_n（t）是与n阶自振频率有关待求解的时间函数。

利用振型正交性可以得到式（27）的微分方程。

利用杜哈梅积分可以求得式（27）微分方程的特解为

2 锚杆-围岩结构耦合振动的数值模拟

2.1 锚杆-围岩结构自由振动的数值模拟

基础算例的支护参数设定为：锚杆杆体材料采用HRB400级普通热轧左旋无纵肋螺纹钢，锚固段灌浆采用M25水泥砂浆，锚固段长度取1.5 m，自由段长度1 m，锚杆间距1.5 m；选取钻孔直径28 mm，锚杆直径20 mm。利用MATLAB软件计算得出前5阶自振频率依次为：55.975 647、66.107 850、77.128 141、113.934 32、135.487 375 Hz。

1）杆体材料对结构自振的影响

锚杆支护材料的强度等级一般取HRB335级、HRB400级和HRB500级钢筋，其弹性模量的取值均为200 GPa。通过式（2）可以看出，杆体弹性模量相同，单根锚杆刚度、梁间锚杆分布刚度也相同。同时，改变钢筋等级也不会引起其他参数的改变。不考虑锚杆断裂失效，在一定范围内提高杆体钢筋强度，并不会对锚杆-围岩结构的耦合振动造成影响。

2）灌浆材料对结构自振的影响

灌浆材料的改变主要会引起锚固段组合体弹性模量值的变化，但与杆体弹性模量相比，灌浆材料弹性模量过小，可以忽略不计。因此，保证锚杆正常工作的情况下，一定范围内增大水泥砂浆的标号对锚杆-围岩结构的耦合振动特性造成的影响可以忽略不计。

3）钻孔直径对结构自振的影响

其他支护参数不变，钻孔直径分别取为23、25、30、32、35 mm，计算出不同钻孔直径下，梁间锚杆分布刚度为：11 170.56、11 170.46、11 171.34、11 171.00、11 171.44 kN/m²。可见，在一定范围内增大钻孔直径对梁间的分布刚度K及其他参数几乎无影响，进而对锚杆-围岩结构的耦合振动无影响。

4）锚固段长度、锚杆间距及锚杆直径对结构自振的影响

其他支护参数不变，依次分别改变锚固段长度、锚杆间距及锚杆直径，得到锚杆-围岩结构的自振频率ω随锚固段长度、锚杆间距及锚杆直径的变化趋势，如图3所示。

由图3可知，前3阶频率较为接近，第4、第5阶频率有明显增长。随着锚固段长度的增加，结构的前4阶自振频率均呈现减小趋势，而第5阶自振频率呈现出增大趋势，如图3（a）所示；随着锚杆间距的增大，结构前五阶自振频率均呈现下降趋势（如图3（b）所示；随着锚杆直径的增大，锚杆-围岩结构的前5阶自振频率均呈现上升趋势，如图3（c）所示。

2.2 锚杆-围岩结构受迫振动的数值模拟

通过对结构自由振动的分析发现：锚固段长度、锚杆间距及锚杆直径会对锚杆-围岩结构的振动特性产生影响。因此，对结构的受迫振动分析仅针对上述3个因素进行。

为模拟锚杆-围岩结构的受迫振动情况，在上述模型（图1）中上方岩梁的中点加一简谐荷载

参考文献[19]的相关研究成果，考虑地面100 kg当量的炸药作用，结构距地面15 m，爆炸产生的压强大约为0.1 MPa。拟合曲线如图4所示。该爆炸将在结构中引起1 500 kN的作用力，取F₀=1 500 kN。f为外界激励荷载的频率。

2.2.1 基础算例下结构受迫振动的动力响应

利用MATLAB软件计算得出基础算例支护参数下，结构上下岩梁中点处的位移响应随外界激励荷载频率的变化情况，如图5所示。由图5可知，上下岩梁中点处位移对频率的响应图形与该种情况下结构自由振动的振型相呼应，侧面证明了数值模拟的正确性。

2.2.2 锚固段长度、锚杆间距及锚杆直径对结构动力响应的影响

其他条件不变，依次分别改变锚固段长度、锚杆间距及锚杆直径，观察锚杆-围岩结构在不同频率激励荷载作用下的动力响应，得到上下岩梁动力反应最大值的变化情况如图6所示。

随着锚固段长度增大，锚杆-围岩结构的动力反应最大值呈减小趋势，如图6（a）、（b）所示。特别是当锚固段长度由1.0 m增大到1.5 m时，上梁的动力反应最大值缩减超过77%，下梁的动力反应最大值缩减超过67%；当锚固段长度增加到2.5 m时，对动力反应的减弱已达到较高水平；继续增加锚固段长度，结构动力反应缩减得十分缓慢，减震效果不再显著。同时，增加锚固段长度使得材料使用量增多，从经济上考虑也不实用。

随着锚杆间距的增大，结构上下梁的动力反应呈现出先减小后增大的趋势。

如图6（c）所示，锚杆间距取1.5 m时，上梁动力反应最小。其中，锚杆间距由1.0 m增大到1.5 m时，其动力反应缩减了约26%；增大到2.2 m时，其动力反应增大了约11%。

如图6（d）所示，锚杆间距取2.2 m时，下梁动力反应最小。其中，锚杆间距由1.0 m增大到1.5 m时，其动力反应缩减了约10%；增大到2.2 m时，其动力反应缩减了约77%。综合考虑，针对所分析的锚杆-围岩结构，当锚杆间距取2.2 m左右时最为合理。

增大锚杆直径对锚杆-围岩结构的影响较复杂：如图6（e）所示，随着锚杆直径增大，上梁动力反应呈现出先减小后增大的趋势：当锚杆直径由14 mm增大到22 mm时，其动力反应持续降低到最小值，缩减了约36%；继续增加锚杆直径，上梁动力反应呈现出增大趋势。如图6（f）所示，随着锚杆直径增大，下梁动力反应持续增大。当锚杆直径由14 mm增大到22 mm时，其动力反应增大了约37%。

由此可见，对于锚杆-围岩整体结构而言，增大锚杆直径会使上下梁的动力反应朝着相反的方向发展，并且变化幅度近乎一致。但考虑到上下梁的动力反应对于结构的整体安全来说有权重上的差别，即下方岩梁的动力反应更加需要被关注。因此，在锚杆能提供必要强度的前提下，可将锚杆直径适当减小。

2.2.3 支护参数优化的安全性验算

需要指出的是，上述参数优化是从锚杆-围岩系统的减震角度出发考虑。与此同时，也应该关注到锚杆支护本身能否达到安全使用的要求。为此，在本文讨论的背景下，结合得到的优化参数，也即锚杆锚固段长度2.5 m、锚杆间距2.2 m，锚杆直径0.02 m，利用有限元软件GTS NX建立二维模型，验证支护体系的安全性，如图（7）所示。

其中，岩土材料采用平面应变单元，采用理想弹塑性本构，以摩尔-库倫强度理论为屈服准则。所讨论的岩土材料为Ⅲ级围岩，其物理力学参数参照《公路隧道设计规范  第一册  土建工程》（JTG  33701—2018）中的围岩物理力学参数输入。锚杆采用HRB400钢筋材料，弹性本构，锚固段与围岩材料节点耦合，自由段仅在端点处与悬吊的围岩节点耦合。

计算中，假定松动圈范围内岩土体处于松动状态，也即与上部围岩脱离，以此考虑锚杆支护的不利工况。

经计算得出锚杆的轴向应力图，如图（8）所示，锚杆最大拉应力发生在自由段，为352 MPa，尚处于HRB400级钢筋的抗拉强度标准值400 MPa的强度范围之内，说明上述出于减震考虑得到的优化参数能满足锚杆支护的安全使用要求。

3 结论

1）在满足使用要求的前提下，改变锚杆杆体材料强度、灌浆材料强度和钻孔直径对于锚杆-围岩结构的动力特性几乎无影响。

2）随着锚固段长度的增加，锚杆-围岩结构的动力响应呈现较明显的降低趋势，在算例中，当锚固段长度增加到2.5 m之后，其对结构整体的减振影响不再显著。在进行锚杆支护设计时，可以设置一个相对合适的锚固段长度来达到较好的减振效果。

3）随着锚杆间距的增加，锚杆-围岩结构的动力响应呈现先减小后增大的趋势。在进行锚杆支护设计时，可以通过改变锚杆间距来达到较好的减振效果。

4）锚杆直径对锚杆-围岩结构振动产生的影响比较复杂：随着锚杆直径的增加，结构上部的动力响应先减小后增大，结构下部的动力响应持续增大。从实际出发，降低锚杆-围岩结构下部的动力响更能保证工程的安全。所以，在保证结构强度的前提下，建议适当减小锚杆直径，以达到减振的目的。另外，使用小直径锚杆，也可实现经济上的节约。

参考文献

[1]  康红普. 我国煤矿巷道围岩控制技术发展70年及展望[J]. 岩石力学与工程学报， 2021， 40（1）： 1-30.

KANG H P. Seventy years development and prospects of strata control technologies for coal mine roadways in China [J]. Chinese Journal of Rock Mechanics and Engineering， 2021， 40（1）： 1-30. （in Chinese）

[2]  KANG H P， YANG J H， MENG X Z. Tests and analysis of mechanical behaviours of rock bolt components for China，s coal mine roadways [J]. Journal of Rock Mechanics and Geotechnical Engineering， 2015， 7（1）： 14-26.

[3]  康红普， 林健， 吴拥政， 等. 锚杆构件力学性能及匹配性[J]. 煤炭学报， 2015， 40（1）： 11-23.

KANG H P， LIN J， WU Y Z， et al. Mechanical performances and compatibility of rock bolt components [J]. Journal of China Coal Society， 2015， 40（1）： 11-23. （in Chinese）

[4]  王爱文， 潘一山， 赵宝友， 等. 吸能防冲锚杆索-围岩耦合振动特征与防冲机理[J]. 煤炭学报， 2016， 41（11）： 2734-2742.

WANG A W， PAN Y S， ZHAO B Y， et al. Coupling vibration characteristics of rock mass and energy-absorption bolt and its anti-impact mechanism [J]. Journal of China Coal Society， 2016， 41（11）： 2734-2742. （in Chinese）

[5]  胡帅伟， 陈士海. 爆破振动下围岩支护锚杆动力响应解析解[J]. 岩土力学， 2019， 40（1）： 281-287.

HU S W， CHEN S H. Analytical solution of dynamic response of rock bolt under blasting vibration [J]. Rock and Soil Mechanics， 2019， 40（1）： 281-287. （in Chinese）

[6]  吉凌， 周传波， 张波， 等. 大断面隧道爆破作用下围岩动力响应特性與损伤效应研究[J]. 铁道学报， 2021， 43（7）： 161-168.

JI L， ZHOU C B， ZHANG B， et al. Study on dynamic response and damage effect of surrounding rock in large tunnel under blasting excavation [J]. Journal of the China Railway Society， 2021， 43（7）： 161-168. （in Chinese）

[7]  李壮， 王俊， 宁建国， 等. 预紧力对锚固体抗动载冲击能力影响的试验研究[J]. 中国矿业大学学报， 2021， 50（3）： 459-468.

LI Z， WANG J， NING J G， et al. Experimental research on influence of pre-tension on dynamic load impact resistance of anchorage body [J]. Journal of China University of Mining & Technology， 2021， 50（3）： 459-468. （in Chinese）

[8]  HE M C， GONG W L， WANG J， et al. Development of a novel energy-absorbing bolt with extraordinarily large elongation and constant resistance [J]. International Journal of Rock Mechanics and Mining Sciences， 2014， 67： 29-42.

[9]  SPEARING A J S， HYETT A J， KOSTECKI T， et al. New technology for measuring the in situ performance of rock bolts [J]. International Journal of Rock Mechanics and Mining Sciences， 2013， 57： 153-166.

[10]  ZHANG K， ZHANG G M， HOU R B， et al. Stress evolution in roadway rock bolts during mining in a fully mechanized long wall face， and an evaluation of rock bolt support design [J]. Rock Mechanics and Rock Engineering， 2015， 48（1）： 333-344.

[11]  刘海雁， 左建平， 刘德军， 等. 基于正交矩阵分析的巷道锚杆支护优化[J]. 采矿与安全工程学报， 2021， 38（1）： 84-93.

LIU H Y， ZUO J P， LIU D J， et al. Optimization of roadway bolt support based on orthogonal matrix analysis [J]. Journal of Mining & Safety Engineering， 2021， 38（1）： 84-93. （in Chinese）

[12]  张明磊， 张益东， 季明， 等. 基于模糊可拓综合评价方法的巷道支护参数优化[J]. 采矿与安全工程学报， 2016， 33（6）： 972-978.

ZHANG M L， ZHANG Y D， JI M， et al. Roadway support parameter optimization based on fuzzy extension synthetic evaluation [J]. Journal of Mining & Safety Engineering， 2016， 33（6）： 972-978. （in Chinese）

[13]  赵东平， 王卢伟， 喻渝， 等. 隧道系统锚杆研究现状与发展方向[J]. 土木工程学报， 2020， 53（8）： 116-128.

ZHAO D P， WANG L W， YU Y， et al. Research status and development direction of tunnel system bolt [J]. China Civil Engineering Journal， 2020， 53（8）： 116-128. （in Chinese）

[14]  令狐可， 武运成， 贾乾祥. 岩石锚杆水平刚度系数的计算方法[J]. 建筑技术， 2006， 37（11）： 860-862.

LINGHU K， WU Y C， JIA Q X. Calculation method for horizontal stiffness coefficient of rock anchor [J]. Architecture Technology， 2006， 37（11）： 860-862. （in Chinese）

[15]  邬爱清， 柳赋铮. 国标《工程岩体分级标准》的应用与进展[J]. 岩石力学与工程学报， 2012， 31（8）： 1513-1523.

WU A Q， LIU F Z. Advancement and application of the standard of engineering classification of rock masses [J]. Chinese Journal of Rock Mechanics and Engineering， 2012， 31（8）： 1513-1523. （in Chinese）

[16]  许宏发， 陈锋， 王斌， 等. 岩体分级BQ与RMR的关系及其力学参数估计[J]. 岩土工程学报， 2014， 36（1）： 195-198.

XU H F， CHEN F， WANG B， et al. Relationship between RMR and BQ for rock mass classification and estimation of its mechanical parameters [J]. Chinese Journal of Geotechnical Engineering， 2014， 36（1）： 195-198. （in Chinese）

[17]  SERAFIM J L， PEREIRA J P. Considerations of the geomechamics classification of Bieniawski [C]// Proceedings of the International Symposium Engineering Geology and Underground Construction. Lisbon： Portugal， 1983： 33-44.

[18]  郗鵬程， 伍法权， 包含. 基于统计岩体力学的隧道围岩分级方法[J]. 地下空间与工程学报， 2018， 14（1）： 131-137.

XI P C， WU F Q， BAO H. A tunnel surrounding rock masses classification method based on statistic mechanics of rock masses [J]. Chinese Journal of Underground Space and Engineering， 2018， 14（1）： 131-137. （in Chinese）

[19]  罗昆升， 王勇， 赵跃堂， 等. 地铁区间隧道在地面爆炸荷载作用下的数值模拟[J]. 解放军理工大学学报（自然科学版）， 2007， 8（6）： 674-679.

LUO K S， WANG Y， ZHAO Y T， HUANG L K.， et al. Numerical simulation of section subway tunnel under surface explosion [J]. Journal of PLA University of Science and Technology （Natural Science Edition）， 2007， 8（6）： 674-679. （in Chinese）

（编辑  王秀玲）