露天矿山岩质边坡软弱夹层赋存状态影响边坡稳定性规律研究

樊鸿志 王光进 蓝蓉 刘明生

doi：10.11835/j.issn.1000.582X.2024.04.003

收稿日期：2023-11-01

基金项目：国家自然科学基金资助项目（52174114）；国家磷资源开发利用工程技术研究中心开放基金资助项目（NECP2022-07）。

Foundation：Supported by National Natural Science Foundation of China （52174114）， and the Open Foundation of the National Engineering Research Center for Phosphorus Resources Development and Utilization （NECP2022-07）.

作者簡介：樊鸿志（1998—），男，硕士研究生，主要从事矿山边坡灾害研究，（E-mail）2278620781@qq.com。

通信作者：王光进，男，教授，博士生导师，主要从事矿山岩土边坡灾害预警研究，（E-mail）wangguangjin2005@163.com。

摘要：软弱夹层作为一种典型地质结构是影响整个边坡安全稳定性的关键因素。为了更好地分析软弱夹层的性质及对边坡稳定性的影响，针对某含软弱夹层矿山露天岩质边坡，运用正交对照法对边坡软弱夹层的埋深、倾角、数量及夹层间结构面间距等4种夹层赋存状态，进行变量4×4正交模拟，揭示了不同赋存状态下边坡稳定性及变形规律。研究结果表明，1）边坡软弱夹层的赋存状态对边坡稳定性有显著影响，随软弱夹层埋藏深度的增加边坡安全系数随之增大，当埋深达到一定值后，边坡安全系数趋于稳定；2）随着软弱夹层角度的增大，破坏机制表现为层间错动、顺层蠕滑和沿软弱结构面的剪切滑移递进式变化；3）随软弱夹层层数增多，边坡整体性下降致使变形不均匀，边坡安全系数减小，水平方向位移增大；4）对比同等埋深结构面间距较小的软弱夹层边坡，结构面间距对边坡安全系数的影响较小。

关键词：露天边坡；软弱夹层；赋存状态；安全稳定性；边坡变形

中图分类号：TD804           文献标志码：A            文章编号：1000-582X（2024）04-022-12

Influence of the occurrence state of soft interlayer on the rock slope of open-pit mine

FAN Hongzhi1， WANG Guangjin1，2， LAN Rong3， LIU Mingsheng3

（1. Faculty of Land Resources Engineering， Kunming University of Science and Technology， Kunming 650093， P. R. China; 2. Yunnan International Technology Transfer Center for Mineral Resources Development and Solid Waste Resource Utilization， Kunming 650093， P. R. China; 3. China Nonferrous Metal Industry Kunming Survey Design Institute Co.， Ltd.， Kunming 650051， P. R. China）

Abstract： As a typical geological structure， a soft interlayer is a key factor affecting the safety and stability of the entire slope. In order to better analyze the properties of soft interlayers and their influence on slope stability， the orthogonal control method was used to simulate four occurrence states of the sandwich depth， inclination angle， quantity and structural surface spacing between the layers of the slope with a soft interlayer in a mine open-pit rock slope. A 4×4 orthogonal simulation was carried out and the stability and deformation law of the slope were revealed under different occurrence states. The results show that： 1） the occurrence state of the soft and weak interlayer of the slope has a significant impact on the stability of the slope. The safety factor of the slope increases with the increase of the burial depth of the soft interlayer， and the safety factor tends to stabilize after the burial depth reaches a certain level. 2） With the increase in the angle of the soft interlayer， the failure mechanism is manifested as interlayer mismotion， creep slip along the layer and progressive change of shear-slip along the soft structural surface. 3） The increase in the number of soft interlayer layers leads to an overall decline in the slope with uneven deformation， a decrease in the safety factor of the slope， and an increase in horizontal displacement. 4） For the soft sandwich slope with the same buried depth， structural surface spacing has less influence on the slope safety factor when the spacing is small.

Keywords： open slopes; weak interlayer; endowment status; security and stability; slope deformation

矿山开采过程中常遇到边坡含软弱夹层的问题，这种岩质边坡的存在对矿山的稳定性和变形产生了重大影响。软弱夹层具有较低的强度和稳定性，容易出现滑动、断裂和塌陷等不稳定现象。因此，矿山边坡的稳定性和变形特征与软弱夹层的状态密切相关[1]。

目前，相关学者关于软弱夹层对边坡稳定性及变形的研究已取得一定的进展。例如，王来贵等[2]结合工程实例以露天矿山剖面为研究对象，模拟含软弱夹层顺层岩质边坡的变形、破坏及滑动演化过程；宋洋等[3]利用缩尺实验开展考虑夹层埋深、岩层倾角、含水率因素影响下岩体剪切蠕变特性实验；陈权川等[4]运用一种基于尖点突变理论的突变级数法，对边坡软弱夹层的6个因素进行正交实验，得出影响含软弱夹层缓倾顺层岩质边坡稳定性的主控因素的敏感程度大小顺序；Tien等[5]对软弱夹层倾角及其岩石强度和弹性模量的关系进行了探究，并建立了能够反映软弱夹层倾角作用的破坏准则。刘杨等[6]基于饱和-非饱和渗流理论，模拟降雨工况下矿山边坡的渗流过程，得出软弱夹层会阻碍降雨渗流通道，导致孔压曲线发生变形；Zheng等[7]通过不同频率下循环三轴载荷实验对不同倾角的非连续节理泥岩试样进行研究，裂隙沿节理向试样的两端扩展导致泥岩试样产生损伤；范昊等[8]利用工程地质分析和颗粒离散元软件MatDEM对比分析了含和不含软弱夹层2种开挖情况，得出软弱夹层的存在会对边坡开挖的稳定性产生较大的影响；范刚等[9]、Chen等[10]和Wang等[11]设计开展了软弱夹层振动台模型实验，分析地震作用下含软弱夹层顺层岩质斜坡动力响应规律；Fan等[12]研究了含软弱夹层岩质边坡在反倾和顺层下的动力响应规律，并对比分析了2种边坡的破坏机制；Zhu等[13]采用传感等技术对边坡应变特征进行实时监测，从而更精确地对边坡稳定性进行评价。张社荣等[14]基于Sarma极限平衡法和有限元强度折减法分析岩质边坡在不同条件下的安全系数变化规律，揭示了多层软弱夹层边坡岩体的破坏机制及稳定性特征；尤耿明等[15]和Zhu等[16]系统分析了软弱夹层赋存状态多因素影响下边坡的位移变形演化规律及夹层蠕变规律，并借助Burgers本构模型，探讨了含软弱夹层矿山边坡的长期稳定性。

基于此，由于地质构造环境的不同，软弱夹层岩质边坡影响因素各异，主要有以下几类：1）岩体与软弱夹层的物理力学性质；2）软弱夹层几何参数（埋深、倾角、夹层数量、夹层间结构面间距等）；3）初始地应力、水文气象、地震和人工作用等。但是关于露天矿山岩质边坡软弱夹层赋存状态对边坡稳定性及变形的影响的研究深度与系统性还不够，因此，以云南某露天矿山含软弱夹层岩质开采边坡为基础，研究矿山岩质边坡软弱夹层赋存状态对边坡稳定性及变形的影响。基于Bishop法和有限元强度折减法，探讨岩质边坡在不同软弱夹层埋深、倾角、夹层数量、夹层间结构面间距条件下的安全系数与边坡位移的变化规律，从而揭示含软弱夹层岩质边坡的变形及稳定性特征。力求通过分析边坡的稳定性和变形特征，为矿山设计及施工提供科学依据，减少矿山灾害的发生[17]。

1 工程概况及模型建立

1.1 工程概况

云南某大型磷资源露天开采矿山，边坡岩体结构类型为层状结构，层间有水云母黏土岩软弱夹层发育。其边坡岩体主要为白云岩及砂质白云岩，含有2层水云母黏土岩软弱夹层。此类软弱夹层含泥质、粉砂质物质，因此岩体抗风化能力差，层面黏结性差。岩体常规物理力学参数如表1所示。

1.2 模型建立

该典型矿山含软弱夹层岩质边坡呈东-西走向。该矿山边坡上部已经开挖成了5个台阶，分别是2190平台、2160平台、2130平台、2100平台和2070平台。边坡角度约为45°，边坡的最大高差为160 m。剖面位置选取边坡整体最大高程处，剖面包含软弱夹层及边坡所有平台且平台较为清晰，因此选取此剖面具有较好的代表性。典型剖面选取如图1所示。

剖面模型长230 m，选取高程2 030～2 190 m，总高度H=160 m，厚度25 m，软弱夹层厚度为h=3.61 m，夹层夹角为15°。采用犀牛软件建模与网格划分（网格边长1～5 m），共26 509网格38 797节点，并将边坡模型导入到FLAC 3D中得到，剖面模型图如2所示。边坡在自然工况下设置边界条件为左右两侧施加法向约束，上部为自由边界，下部为底板固定约束。

2 软件模拟

2.1 方法介绍

2.1.1 Bishop法

Bishop法是一种极限平衡条分法，将圆弧滑面垂直方向分成n条，该法忽略竖向条间剪力，根据整体力矩平衡条件求解安全系数。由于该方法满足土条间的水平推力平衡条件，其精度要高于瑞典圆弧法。Bishop法力学模型如图3所示。

该法的计算参数：Fs为滑面安全系数、R为圆弧滑面半径、bi为第i条块宽度、Wi为第i条块重力、αi为第i条块圆弧底面倾角、Xi和Xi+1为第i与i+1条块间横向力、Ei和Ei+1为第i与i+1条块间纵向力、Ti为第i条块圆弧底面剪力、Ni为第i条块法向作用力、ui为第i条块孔隙水压力。其计算公式为：

，    （1）

。    （2）

式中：Ei及Xi表示法向及切向條间力；Wi为i条块自重；Qi为水平力；ci为材料黏结力和i为材料内摩擦角；ei为第i条块重心到滑弧圆心的垂直距离。

2.1.2 强度折减法

传统强度折减法是一种常用于边坡稳定性分析的方法，其原理基于材料的强度折减。在应用该方法时，首先建立边坡的力学模型，再根据不同的受力情况（如坡面滑动、坡脚滑移等），计算出边坡在不同情况下的安全系数。然后，按照一定的强度折减系数，将边坡的强度参数进行折减，重新计算安全系数，直到得到符合要求的安全系数，即为边坡安全系数[18]。

强度折减系数的计算公式如下，

，    （3）

式中：k为强度折减系数；m为强度折减的比例；n为强度折减的次数。在边坡稳定性分析中，通常将m取为较小的值（如0.1），n取为较大的值（如10），以保证计算结果的精度。

强度折减后的边坡强度参数可以用以下公式计算：

，    （4）

。    （5）

式中：C'和φ'分别为强度折减后的剪切强度和内摩擦角；C和φ为原始的剪切强度和内摩擦角。在计算边坡安全系数时，需要使用强度折减后的强度参数进行计算。

2.2 模拟方案设计

根据对矿山现场勘察结果及其勘察地形图，在采场边坡带有软弱夹层的凌空面选取代表性剖面作为研究对象，如图2剖面结构图。依托大量工程案例并结合所研究矿山边坡实际工程背景，基于Bishop法与强度折减法对含软弱夹层矿山岩质边坡的夹层埋藏深度、夹层倾角、夹层数量及夹层间结构面间距4种软弱夹层赋存几何状态进行数值模拟研究（见图4），模拟方案如表2所示，其中，h=3.61 m为单层夹层厚度，H=160 m为选取截面的总高程，物理力学性质参数如表1所示，力求探究在软弱夹层不同几何赋存状态下含软弱夹层岩质边坡稳定性的内在规律。

3 软弱夹层赋存状态对边坡稳定性影响

3.1 埋藏深度影响分析

基于Bishop法与强度折减法分析矿山岩质边坡软弱夹层不同埋深对边坡稳定性的影响。采取固定15°倾角，软弱夹层为2层，夹层间结构距离2h=7.22 m，选取截面右侧上层软弱夹层埋深作为研究基准点，分别取距离上凌空面0.1H=16 m、0.3H=48 m、0.5H=80 m、0.7H=112 m（H=160 m为选取截面的总高程）作为研究对象，如图4（a）所示。采用FLAC 3D软件研究其安全系数与水平方向位移变化情况，同时对照其在x（水平）方向位移云图，如图5所示。

由图5可以看出，软弱夹层埋藏深度从0.1H到0.5H时，安全系数与软弱夹层埋藏深度呈正相关，软弱夹层埋藏深度越浅其对边坡稳定性影响越大。随着深度加深，对应安全系数增大，当埋藏深度达到一定值（0.5H=80 m）时，边坡稳定性系数保持不变。基于此，当软弱夹层深度在达到一定值时，对边坡稳定性影响微小至可忽略不计。2种方法对比可知，2种方法所得安全系数大小相近，由于Bishop法没有考虑岩体本身的变形，其计算所得的安全系数略大于强度折减法的计算结果，而当安全系数较小时，这种差距会增大。边坡软弱夹层埋藏深度与边坡x方向最大位移呈负相关，随着埋藏深度的增加，水平方向位移减小与安全系数增大相对应。

结合图6可知，软弱夹层埋深对含软弱夹层岩质边坡失稳破坏变形的影响明显，随着埋深的逐渐增大，含软弱夹层岩质边坡水平方向位移减小，最大位移区集中在软弱夹层的出露位置，在边坡最上层软弱夹层出露位置呈现最大水平位移区域，位移方向主要是沿软弱夹层方向进行顺层滑移，且滑移面的滑出口位于软弱夹层出露位置。

当软弱夹层埋藏深度为0.5H=80 m时，软弱夹层对边坡水平方向位移影响较小，位移主要受基岩位移的影响；当软弱夹层埋藏深度为0.7H=112 m时，软弱夹层埋深已经低于边坡整体滑移带，对边坡水平位移基本不产生影响。

3.2 岩层倾角影响分析

在本节中，以图2（a）边坡剖面模型图做基础，基于Bishop法与强度折减法探讨含软弱夹层的岩质边坡在不同倾角下，软弱夹层赋存状态对边坡岩体变形机制及稳定性的影响。考虑到软弱夹层其他几何状态对边坡稳定性的影响，采用控制变量法，选取2条软弱夹层，埋深控制在0.5H=80 m，倾角取5°～35°，不同倾角模型如图4中文格式（b）所示。

经计算，在5°～35°倾角下，软弱夹层边坡安全系数与最大水平位移如图7所示，Bishop法与强度折减法计算所得边坡安全系数随软弱夹层角度变化规律基本一致，软弱夹层角度在5°～35°范围内与边坡安全系数

呈现负相关，随着夹层角度增加，安全系数值减小。当倾角大于15°时，边坡安全系数呈加快下降趋势且角度越大安全系数减小越快。由于2种方法计算原理不同，故计算所得安全系数具有一定的差别，当软弱夹层倾角在5°和35°时差距较大。Bishop法所求安全系数大于同倾角下强度折减法计算结果，这主要是由于Bishop法基于极限平衡原理，假定边坡为剪切破坏。而强度折减法在抗剪强度一定的情况下，上部岩体易出现拉裂破坏，因为岩体的抗拉强度较小，强度折减法所得的安全系数相对较小[14]。软弱夹层角度在5°～35°范围内与边坡水平方向位移呈现正相关，随着夹层倾角增加水平最大位移值逐渐增大。

不同软弱夹层倾角条件下边坡的x方向位移与应变区域位置差异较大，如图8所示，随着软弱夹层倾角的增大，边坡滑裂带逐渐变浅，较大应变区域面积增大且集中于软弱夹层上部，滑出口逐渐向坡址推进；由边坡x方向位移云图看出，随软弱夹层倾角增大边坡岩体破坏大致经历层间错动、顺层蠕滑和沿软弱结构面的剪切滑移几个阶段。

3.3 夹层数量的影响分析

对含有软弱夹层的边坡，边坡中含有软弱夹层的数量对其稳定性有较大的影响，以软弱夹层层数2～5层为例，如图4（c）所示，基于Bishop法与强度折减法探讨软弱夹层层数对多层软弱夹层边坡岩体破坏机制及其穩定性的影响，其边坡内软弱夹层角度为15°，在2～5层软弱夹层不同工况下计算结果如图9所示。

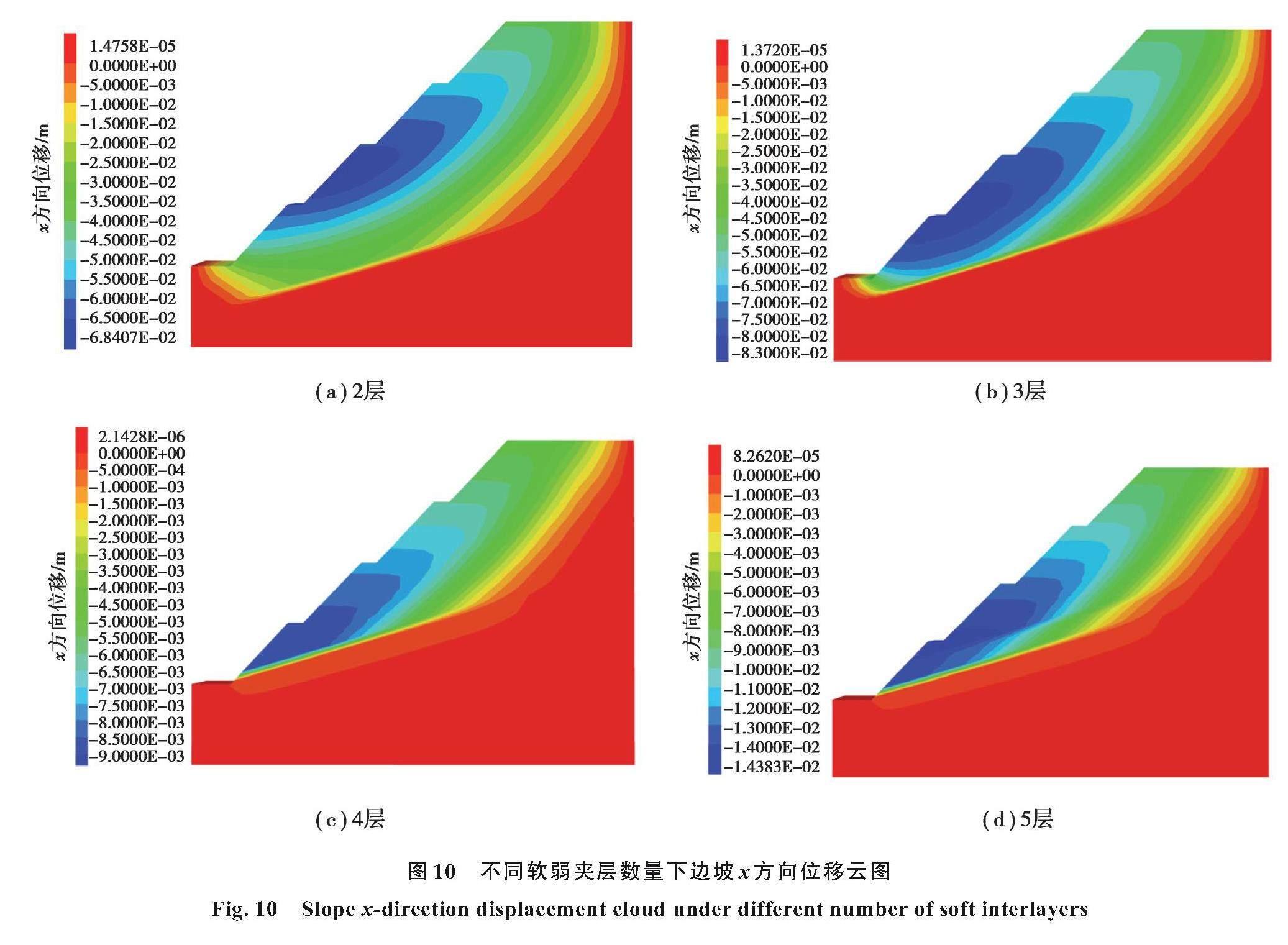
控制软弱夹层角度及层间厚度研究不同软弱夹层数量对矿山开采边坡稳定性的影响，如图9所示。基于Bishop法与强度折减法，软弱夹层数量在2～5层时边坡安全系数变化趋势基本相同，当边坡中存在的软弱夹层数量增加，会导致边坡整体刚度降低从而使得边坡安全系数减小，且边坡安全系数下降趋势加快，软弱夹层层数为2层时安全系数最大，边坡最稳定。随边坡软弱夹层层数的增加，x方向位移随之增大，在从4层增加到5层阶段，x方向位移变化尤为明显，最大位移达到14.383 mm，由此看出软弱夹层数量对边坡稳定性起负面作用。

由图10看出，边坡变形区域主要集中在最上层软弱夹层，潜在破坏面主要集中在前缘，受最上层软弱夹层影响较大；对比图10，随着边坡内软弱夹层数量增加，边坡整体刚度下降使得边坡在受到外力作用时更容易发生水平方向的位移[19]。从图10（d）看出，多层软弱夹层的存在会导致边坡的整体变形不均匀，可能引起边坡的局部滑动或变形集中。

3.4 结构面间距影响分析

对含软弱夹层的边坡，不同结构面间距条件下边坡的安全系数存在一定差距。以边坡软弱夹层2层，倾角15°为例，模型图如图4（d）所示，下层软弱夹层位置不变探讨软弱夹层结构面间距对边坡稳定性的影响。由图11可知，边坡变形主要受上层软弱夹层埋深影响，故为排除软弱夹层埋深变化对模拟结果的影响对比同等埋深下软弱夹层结构面间距为2h（h=3.61 m为单层夹层厚度）的边坡，计算结果如图12所示（1为不同软弱夹层结构面间距数据、2为同埋深下软弱夹层结构面间距2h对照数据）。

由图11～12可知，在不同夹层间距条件下，基于Bishop法与强度折减法2种方法所求得安全系数的变化规律基本一致，边坡安全系数均随着结构面间距增大而减小，边坡稳定性随之下降；对比同等埋深下2h软弱夹层间距的安全系数与x方向位移，随着夹层间结构面间距的增加（对比较小间距）边坡安全系数减小，对比图12，x方向位移1和2，边坡x方向位移差值随着软弱夹层间距增大而变大，其主要由下部软弱夹层对基岩的扰动导致边坡整體稳定性下降[20]。由图11（c）（d）的对比可知软弱夹层结构面间距在6h～8h之间时，上层软弱夹层出露位置从坡址提升到临空面出露，此时x方向位移变化较大，且对应边坡安全系数也下降较快。

4 结  论

1）软弱夹层埋深对含软弱夹层岩质边坡稳定性影响显著，随着软弱夹层埋藏深度的增加，边坡安全系数增加的同时水平位移减小，在埋深较浅时，软弱夹层对边坡稳定性影响较为显著；随埋深的增大，软弱夹层对边坡稳定性影响逐渐减小，当埋深达到一定深度后，边坡安全系数增加缓慢，水平方向位移变化也随之下降。当软弱夹层埋藏深度大于0.5H时，在此深度下，边坡稳定性几乎不受软弱夹层控制。

2）软弱夹层倾角在5°～35°范围内时，随软弱夹层倾角的增加，边坡岩体破坏大致经历层间错动、顺层蠕滑和沿软弱结构面剪切滑移几个阶段；且边坡滑裂带逐渐变浅，较大应变区域面积增大且集中于软弱夹层上部，滑出口逐渐向坡址推进，边坡稳定性下降。

3）软弱夹层层数对边坡水平方向位移影响较大，随软弱夹层层数增多，边坡安全系数减小，水平方向位移增大；且边坡整体刚度下降使得边坡在受到外力作用时更容易发生水平方向的位移，多层软弱夹层的存在会导致边坡的整体变形不均匀；边坡潜在滑移面主要集中在前缘，受最上层软弱夹层影响较大。

4）对比同等埋深较小结构面间距软弱夹层边坡，结构面间距对边坡安全系数的影响较小。在边坡软弱夹层结构面间距不同的情况下，边坡变形破坏机制基本一致，边坡稳定性主要受最上层软弱夹层埋深位置影响。下层软弱夹层对基岩的扰动导致边坡水平位移增加，结构面间距的增大会导致边坡整体的刚度降低从而导致安全系数减小。

参考文献

［1］  张家明. 含软弱夹层岩质边坡稳定性研究现状及发展趋势[J]. 工程地质学报， 2020， 28（3）： 626-638.

Zhang J M. State of art and trends of rock slope stability with soft interlayer[J]. Journal of Engineering Geology， 2020， 28（3）： 626-638. （in Chinese）

［2］  王来贵， 马玮航， 赵娜， 等. 含软弱夹层顺层岩质边坡变形-滑动演化过程研究[J]. 辽宁工程技术大学学报（自然科学版）， 2023， 42（2）： 129-135.

Wang L G， Ma W H， Zhao N， et al. Deformation-sliding evolution process of bedding rock slope with weak interlayer[J]. Journal of Liaoning Technical University （Natural Science）， 2023， 42（2）： 129-135.（in Chinese）

［3］  宋洋， 马旭琪， 赵常青， 等. 隐伏非贯通软弱夹层岩质边坡剪切蠕变特征及稳定性研究[J]. 岩土工程学报， 2024， 46（4）：755-763.

Song Y， Ma X Q，Zhao C Q， et al. Shear creep characteristics and stability of rock slopes with concealed noninterpenetrated weak interlayer[J]. Chinese Journal of Geotechnical Engineering， 2024， 46（4）：755-763.（in Chinese）

［4］  陈权川， 王安礼， 邬忠虎， 等. 基于尖点突变理论的含软弱夹层缓倾顺层岩质边坡稳定性研究[J]. 河南理工大学学报（自然科学版）， 2022， 41（6）： 188-195.

Chen Q C， Wang A L， Wu Z H， et al. Study on stability of gently inclined bedding rock slope with weak interlayer based on cusp catastrophe theory[J]. Journal of Henan Polytechnic University （Natural Science）， 2022， 41（6）： 188-195.（in Chinese）

［5］  Tien Y M， Kuo M C. A failure criterion for transversely isotropic rocks[J]. International Journal of Rock Mechanics and Mining Sciences， 2001， 38（3）：399-412.

［6］  刘杨， 彭亮， 祝鑫， 等. 降雨條件下含缓倾软弱夹层矿山高边坡稳定性分析[J]. 矿业研究与开发， 2022， 42（7）： 71-79.

Liu Y， Peng L， Zhu X， et al. Stability analysis of high slope with gently inclined weak interlayer under rainfall condition in mine[J]. Mining Research and Development， 2022， 42（7）： 71-79.（in Chinese）

［7］  Zheng Q S， Liu E L， Yu D， et al. Fatigue and damage properties of non-consecutive jointed mudstone samples subjected to cyclic triaxial loading[J]. Bulletin of Engineering Geology and the Environment， 2020， 79（5）： 2467-2481.

［8］  范昊， 肖诗荣， 魏瑞琦， 等. 软弱夹层对某矿山边坡稳定性的影响分析[J]. 三峡大学学报（自然科学版）， 2022， 44（1）： 54-59.

Fan H， Xiao S R， Wei R Q， et al. Analysis of influence of weak interlayer on slope stability of a mine[J]. Journal of China Three Gorges University （Natural Sciences）， 2022， 44（1）： 54-59.（in Chinese）

［9］  范刚， 张建经， 付晓， 等. 含软弱夹层顺层岩质边坡动力破坏模式的能量判识方法研究[J]. 岩土工程学报， 2016， 38（5）： 959-966.

Fan G， Zhang J J， Fu X， et al. Energy identification method for dynamic failure mode of bedding rock slope with soft strata[J]. Chinese Journal of Geotechnical Engineering， 2016， 38（5）： 959-966.（in Chinese）

［10］  Chen Z L， Hu X， Xu Q. Experimental study of motion characteristics of rock slopes with weak intercalation under seismic excitation[J]. Journal of Mountain Science， 2016， 13（3）： 546-556.

［11］  Wang K L， Lin M L. Initiation and displacement of landslide induced by earthquake： a study of shaking table model slope test[J]. Engineering Geology， 2011， 122（1/2）： 106-114.

［12］  Fan G， Zhang J J， Wu J B， et al. Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table[J]. Rock Mechanics and Rock Engineering， 2016， 49（8）： 3243-3256.

［13］  Zhu H H， Wang Z Y， Shi B， et al. Feasibility study of strain based stability evaluation of locally loaded slopes： insights from physical and numerical modeling[J]. Engineering Geology， 2016， 208： 39-50.

［14］  张社荣， 谭尧升， 王超， 等. 多层软弱夹层边坡岩体破坏机制与稳定性研究[J]. 岩土力学， 2014， 35（6）： 1695-1702.

Zhang S R， Tan Y S， Wang C， et al. Research on deformation failure mechanism and stability of slope rock mass containing multi-weak interlayers[J]. Rock and Soil Mechanics， 2014， 35（6）： 1695-1702.（in Chinese）

［15］  尤耿明， 王光进， 刘文连， 等. 矿山边坡软弱夹层赋存状态及蠕变特性对边坡稳定性影响研究[J]. 金属矿山， 2021（12）： 200-206.

You G M， Wang G J， Liu W L， et al. Study on the influence of occurrence state and creep characteristics of weak interlayer on mine slope stability[J]. Metal Mine， 2021（12）： 200-206.（in Chinese）

［16］  Zhu S N， Yin Y P， Li B， et al. Shear creep characteristics of weak carbonaceous shale in thick layered Permian limestone， southwestern China[J]. Journal of Earth System Science， 2019， 128（2）： 28.

［17］  方慶红. 含缓倾软弱夹层露天高边坡坡态控制参数优化及稳定性研究[D]. 武汉： 武汉科技大学， 2021.

Fang Q H. Optimization of slope state control parameters and stability study of open-pit high slope with gently inclined weak interlayer[D].Wuhan： Wuhan University of Science and Technology， 2021. （in Chinese）

［18］  郑川. 软弱夹层条件下岩质边坡稳定性分析与治理方案研究[D]. 重庆： 重庆交通大学， 2020.

Zheng C. Stability analysis and treatment scheme of rock slope under the condition of weak interlayer[D].Chongqing： Chongqing Jiaotong University， 2020. （in Chinese）

［19］  戴加祺. 含软弱夹层的岩质边坡稳定性影响因素的定性分析[J]. 西部探矿工程， 2017， 29（12）： 13-15， 19.

Dai J Q. Qualitative analysis of influencing factors on stability of rock slope with weak interlayer[J]. West-China Exploration Engineering， 2017， 29（12）： 13-15， 19.（in Chinese）

［20］  穆成林. 顺层岩质高边坡开挖过程变形失稳演化机制及预测评价研究： 以织金石化场区边坡为例[D]. 成都： 成都理工大学， 2017.

Mu C L. Study on deformation and instability evolution mechanism and prediction evaluation of bedding rock high slope during excavation： a case study of Zhijin petrochemical field slope[D].Chengdu： Chengdu University of Technology， 2017.    （in Chinese）

（编辑  郑洁）