多视角探究2024 年大湾区一模高三数学卷填空压轴题
广东省中山市实验中学(528400) 杨沛娟
大湾区2024 年第一次模拟考试,是广东中山、珠海、江门、韶关等7 市共10 多万学生参加的联考,其试题既有经典呈现,又有体现创新的新型试题.笔者选择该卷颇具经典的填空压轴题,从六个视角进行探究.
1 试题探究
1.1 数形结合
数形结合是研究某些数学问题的首选思想和方法,是通过将抽象的数学概念、定理或问题等与直观的几何图形相结合,以便于理解和解决问题.本题可以结合已知条件与目标函数的几何特征,构造相关图形进行研究.已知函数是抛物线,目标函数可以采用多种方式构造,下面给出解法1 与解法2.
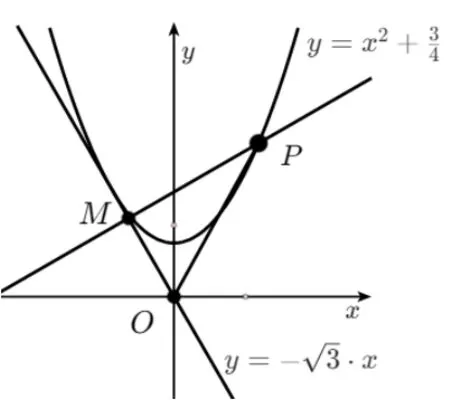
图1
评析此解法需要用到点到直线距离公式,两点间距离公式及直角三角形中的余弦定义式,需要的转化较多,对学生思维的聚焦和发散都有较高要求,借助信息技术动态展示较好理解.
解法2令则过点P(x,y) 的直线l为, Z 为直线l 的纵截距, 根据题意, 现只考虑Z > 0 的情形, 又为点P(x, y) 原点的距离, 如图2 所示.
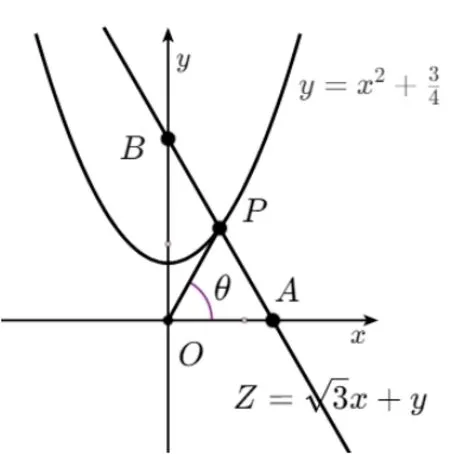
图2
由正弦定理得
评析分母表示点P(x,y)原点的距离,很容易想到分子是否具备几何意义呢? 取目标函数此时Z为直线l的纵截距.此解法与解法1 都是将代数问题转化为几何问题,最后再回归到代数方法解决问题,都体现了数形结合的思想.
1.2 三角函数
利用三角函数求最值是解决最值问题的常用方法,本题将式子合理拆解后,可以利用三角函数定义转化为三角函数求最值问题.
评析此解法主要利用三角函数定义及最值的求法,涉及到基本不等式的基本用法,总体来说比较容易理解和掌握.关键是学生掌握了转化与化归的思想,结合所求式子特征能够进行合理转化.
1.3 向量方法
向量法是解决最值问题的常用方法,本题有所求式子结构联想到向量的夹角公式,转化为求夹角余弦值的最大值问题.
评析此解法涉及到向量的夹角公式和抛物线的切线问题,是学生比较容易掌握的知识点,也是高考热门考点,需要学生熟练掌握.关键点同视角2 类似,要求合理联想,恰当转化.
1.4 导数方法
研究函数的极值,常规方法之一是对函数求导,分析出函数的单调区间,从而得到函数极值.此题的函数表达式较为复杂,能否求导研究呢? 下面给出解法5 直接求导,解法6降次求导.
评析直接对分子和分母均为4 次的函数表达式求导,按函数除法的求导法则逐步求导,在导函数分子的运算过程中,逐步提取公因式,并采用分组分解的方法研究的因式,最难想到的是.对导函数进行因式分解之后,则非常容易得到单调区间,从而得到极值,但该方法计算量大,对考生要求较高.下面给出一种更简洁的导数方法,通过换元后降次,将复杂函数式化为另一个简单函数,然后再进一步通过求导方法研究函数在相应区间上的极值.
评析此解法本质上同解法5 相同,都是利用导数解决问题,只是在解题过程中运用了换元进行降次处理.如何想到换元呢? 观察所研究分式函数,分子与分母都是四次函数,分子分母同时除以x2,经历变形后均含有表达式从而想到令将分子分母的4 次函数降为2 次函数,再求导后研究极值,计算量少了许多.
1.5 换元方法
基本不等式是解决最值问题的常用方法,笔者在用解法6 进行解答时考虑到是否可以用基本不等式求解,下面给出经过换元处理后,利用基本不等式和双勾函数进行求解的两种方法.
评析此解法本质上同解法7 相同,只是处理方式不同.齐次化处理较容易想到,换元后,利用基本不等式和双勾函数求解,是对学生运算素养和思维能力的很好地考查,学生不易掌握该方法.
1.6 高等数学视野
初等数学问题也可以用高等数学知识解决.本题可以用高等数学中的拉格朗日乘数法进行解答.在介绍解法前,先介绍拉格朗日乘数法的定义: 设给定二元函数z=f(x,y)和附加条件φ(x,y)=0,为寻找z=f(x,y)在附加条件下的极值点,构造拉格朗日函数F(x,y,λ)=f(x,y)+λφ(x,y),其中λ为参数.令F(x,y,λ)对x,y和λ的一阶偏导数等于零,即
评析拉格朗日乘数法适用于求解带有等式约束的最优化问题,涉及到偏导数和方程组的求解,这种高等数学视野下的解法可能会导致计算变得更加复杂.相比之下,初等解法会更加简单和直接,多数学生也更容易接受,对于尖子生可以适当拓展.
2 试题溯源
清华大学在2019 年自主招生考试中出现过类似题目,只是约束条件略有不同,下面给出该题及变式,请读者自行研读与解答.
在高中数学教学和学习中,一题多解是常见的现象,这不仅仅是因为数学问题本身可能存在多种解决途径,也因为不同的解题方法能够相互启发,提供不同的视角和深入的理解,这些多样的解题方法并非孤立存在,而是构成了一个相互关联的网络.在这个网络中,每一种方法都扮演着特定的角色,它们既可以独立解决问题,也可以联合起来提供更为强大的解题能力.这种对立统一的关系是数学解题过程中的一大特点,它要求学生在面对问题时能够灵活地运用和转换不同的方法.试题的溯源引导及变式训练可以促进学生对试题的深入理解,在学习过程中形成更为扎实和系统的数学知识结构,更好的把握数学本质,促进数学核心素养的生成.
为了有效地解决数学问题,教师应该致力于培养学生的灵活思考能力.这意味着学生不仅要掌握各种解题技巧,还要能够根据问题的具体情形,选择最合适的方法.这需要学生具备深厚的数学基础知识,对数学概念、原理和定理等有深刻的理解,以及丰富的解题经验.同时,学生还需要能够深入分析问题的本质,识别问题的核心结构,这样才能从根本上提出创新和高效的解决方案.
在提出解决方案后,解题过程并没有结束.交流、反思和总结是解题过程中不可或缺的环节.通过与他人交流,学生可以了解不同的解题方法和思路,拓宽自己的视野.反思和总结则是个人内化的过程,它帮助学生巩固已学知识,提升解题技巧,并对未来的问题解决提供指导.有效的自我评估能够促使学生对自己的解题过程进行批判性思考,从而在未来的学习中取得更大的进步.
高中数学题目的解题过程是一个综合性的思维活动,它不仅需要学生具备扎实的数学基础和灵活的解题思维,还需要学生不断地实践和反思.通过对经典题目的深入探究,学生可以提升自己的解题能力,这不仅包括具体的技巧和方法,还包括对数学思想的理解和应用.在这个过程中,教师的引导和同伴的互助都是非常宝贵的资源.通过这样的学习和训练,学生将能够在数学乃至其他领域展现出更高的问题解决能力.

