基于BO-DKELM的滚动轴承故障诊断
聂新华,秦玉峰,李尚璁
(海军航空大学 岸防兵学院,山东 烟台 264001)
0 引言
旋转机械设备目前正广泛应用于电力、制造和航空等各种工业部门中[1-2]。作为故障诊断领域的一个主要问题,滚动轴承的故障诊断已引起研究人员的广泛关注[3-7]。随着机械设备的复杂化和智能化,设备中普遍安装了大量传感器,这些传感器能够采集到丰富的运行数据。智能故障诊断算法能够挖掘这些数据的深层特征并将其应用于设备的故障诊断中,因此基于数据驱动的故障诊断方法受到了广泛关注并取得了丰硕成果[8-10]。基于深度学习的诊断方法是一种典型的数据驱动方法,该方法通过训练神经网络直接建立样本到故障类别的映射关系,而无需人工提取故障特征,具有更强的适用性。
分类器作为智能故障诊断过程中的关键因素,直接影响着故障诊断的精度。极限学习机(ELM,extreme learning machine)是一种单隐层前馈神经网络(SLFN,single hidden layer forward neural network)学习方法。在网络训练过程中,ELM随机初始化输入权重和偏置并得到相应的输出权重,且不需要更新输入权重和隐层阈值,因此相比于传统的神经网络,ELM具有学习速度快的优点[11-13]。大量研究成果表明:相比于BP神经网络和支持向量机,ELM具有更快的训练速度和更好的泛化能力[14-16],因此ELM在智能故障诊断中具有广泛的应用前景。Gao等人[17]提出了一种集成ELM故障诊断模型;Lei等人[18]将本征时间尺度分解技术与核极限学习机(KELM,Kernel extreme learning machine)相结合对铣削刀具磨损情况进行分类;Chen等人[19]提出了一种求和高斯极限学习机,并成功地应用于输电线路故障诊断;Li等人[20]将ELM与自动编码器(AE,auto encoder)相结合,提出了一种基于稀疏保邻域深度极限学习机的滚动轴承故障诊断新算法;Rodriguez等人[21]提出了一种结合平稳小波变换和奇异值分解的ELM算法对滚动轴承故障进行故障诊断;Ye等人[22]提出了一种基于稀疏贝叶斯极限学习机的故障诊断方法。ELM或KELM等故障诊断模型具有学习速度快、鲁棒性强等优点,然而上述文献未考虑故障诊断模型中的超参数对故障诊断结果的影响,如果超参数设置的不合适可能导致最终的故障诊断结果准确率较低。
针对上述问题,本文提出了一种基于BO-DKELM(Bayesian Optimization-deep Kernel Extreme Learning Machine)的滚动轴承故障诊断方法。由于KELM具有学习速度快、泛化能力强等优点,同时考虑到AE能够充分学习输入数据隐含特征的特点,将AE与KELM进行结合,构建了DKELM模型。DKELM模型中超参数较多,若通过手动随机设置超参数的取值往往无法得到最优的结果。因此进一步利用贝叶斯优化算法对DKELM的超参数进行寻优,构建BO-DKELM故障诊断模型,旨在提高DKELM的故障诊断性能,提高系统的故障诊断能力。
1 DKELM故障诊断模型构建
1.1 KELM基本理论
ELM模型的网络结构与SLFN一致,其区别在于ELM在训练阶段不采用传统BP神经网络中的梯度下降的算法,而采用随机的输入层权重和偏置,输出层权重则通过广义逆矩阵理论计算得到,在计算得到所有节点的权值和偏差后便完成了ELM的训练。区别于传统BP神经网络中的梯度下降算法,ELM以任意连续的概率分布随机对隐含层中权值W和偏置b进行初始化,通过非线性激活函数将输入数据映射到新的高维空间,然后基于最小逼近平方差方法求解输出层权重β。ELM算法具体分析如下:

(1)
式中,βi为连接隐含层与输出层的输出权重;g为激活函数,表示隐含层对于输入样本的响应方式。wi=[wi1,wi2,…,win]T为连接第i个隐含层节点和输入节点之间的权重;bi为偏置。ELM的网络结构如图1所示。

图1 ELM网络结构

(2)
上述方程可以用矩阵形式进行表示:
Hβ=T
(3)
(4)

β*=H+T
(5)
式中,H+表示隐含层输出矩阵H的Moore-Penrose广义逆。
上述方法是基于训练误差最小情况下进行计算的,容易产生过拟合的现象,从而无法获得最优的分类效果。因此对问题进行折中考虑,使得训练误差和输出权值同时达到最小化:
(6)
式(6)可以改写为:
(7)
其中:ξi是第i个样本xi与隐含层输出之间的误差;C1为正则化系数,用来控制误差在最小化问题中的占比。根据KKT条件,引入拉格朗日乘子求解公式:
(8)
其中:αij为拉格朗日乘子。求解公式的优化条件可得:
(9)
根据公式(9)可得如下方程组:
(10)
公式(10)等价于:
(11)
其中:I为单位矩阵。结合公式(5)可以得到ELM网络的输出权值的最小二乘解:
(12)
传统ELM模型采用单隐层结构,在隐含层中设置一定数量的神经元节点,通过非线性激活函数将输入数据映射到高维特征空间,并且数据样本在被映射到高空间后能够线性分离,这与前文中核方法的原理是一致的。所以可以根据核方法基本定理,将ELM对输入矩阵的非线性映射过程利用核函数进行替换,从而提高ELM的非线性逼近能力和稳定性。因此,将核函数引入到ELM中,提出如下KELM算法:
首先应用Mercer’s条件定义核矩阵[23]:
Kij=hi·hj=k(xi,xj)
(13)
其中:Kij为核矩阵K中第i行第j列元素。通过核函数k(xi,xj)将输入样本从n维输入空间映射到高维特征空间。核函数包括RBF核函数、线性核函数和多项式核函数等,通常设定为RBF核:
(14)
式中,δ为核宽度。核参数选择完毕后,则核矩阵K是确定的,因此通过定义核函数则可以将ELM中的随机矩阵HHT替换为确定的核矩阵K。由以上分析可得,KELM模型的求解公式可以表示为:
(15)
因此可得KELM模型输出权值为:
β=(I/C1+K)-1T
在KELM算法中,由于利用核矩阵对随机矩阵HHT进行了替换,因此只需要定义核矩阵k(xi,xj)即可计算得到输出函数的值。同时,因为核函数直接采用内积的形式,在求解输出函数值时不需要主观设定网络隐含层节点数目,也不需要设定隐含层初始权重和偏置。
1.2 自动编码器
AE是一种前馈全连接的对称神经网络,其网络结构如图2所示。
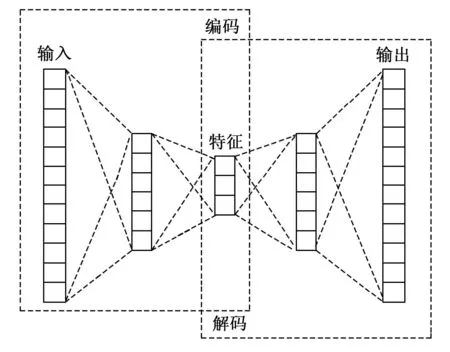
图2 AE网络结构
AE主要由编码层和解码层构成,其中:编码层由输入层和隐含层构成,解码层由隐含层和输出层组成,解码层与编码层的结构类似,且输出与输入的维度相同[24]。AE通过接收、压缩和编码数据,然后以损失最小化为目标,通过无监督训练直到输出尽可能接近地输入数据。其目的在于通过训练学习数据的特征。AE的编码过程为通过激活函数将数据的高维特征降维压缩为隐含层的低维特征表示,实现对输入数据的编码;AE的解码过程为通过激活函数将隐含层的低维特征表示以输入数据为目标进行重构,将输入从编码中重建为原始维度,通过对数据进行编码和解码可以学习到输入数据的隐含特征。AE的数学模型如下:

H=g(w·x+b)
(16)
其中:H为隐含层的输出特征矩阵;w为编码层的权值矩阵;b为编码层的偏置向量;g为激活函数。解码过程为输入数据的重构过程,隐含层输出特征矩阵H的解码过程可以表示为:
(17)
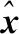
1.3 DKELM模型构建
可以发现若AE仅含有一个隐含层,则ELM与AE在结构上非常相似,因此将AE的思想与ELM相结合中,构造作为自编码器的极限学习机ELM-AE,使ELM的输出重构为输入。ELM-AE的网络结构如图3所示。

图3 作为自动编码器的极限学习机结构
与ELM类似,ELM-AE隐含层输出权重可以由公式转化为:
(18)
其中:C2为ELM-AE的正则化系数。根据ELM-AE的特征学习能力,本文构造了一种深度极限学习机模型,将ELM-AE作为DKELM的基本单元,利用逐层贪婪的训练方法对DKELM进行训练。DKELM的基本思想为:利用AE的特征学习能力,令ELM-AE的输出在最小重构误差的情况下无限接近原始输入,通过多个ELM-AE单元的分层无监督训练确定DKELM中每个隐含层的权重。经过多层ELM-AE单元的训练后,DKELM模型能够深层次地提取输入数据的隐含特征,从而提高最终分类效果。DKELM模型的训练过程如图4所示。
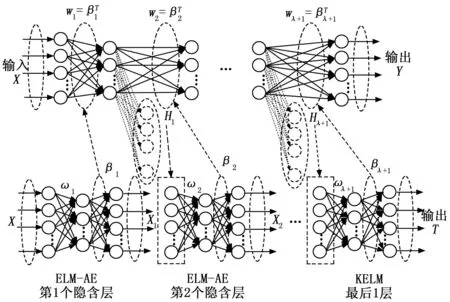
图4 DKELM模型训练过程

根据分析,本文所构建的DKELM模型中包含λ个ELM-AE模型和一个KELM模型。虽然DKELM模型能够用于系统的故障诊断,但是存在以下问题:由于模型中超参数过多,主要包括:DKELM中各隐含层的节点个数nλ,KELM中的正则化系数C1与核参数δ,ELM-AE中的正则化系数C2。各超参数对最终的故障诊断精度都存在着较大影响,若通过手动随机设置各超参数往往无法得到最优的结果。因此本文提出一种BO-DKELM模型,利用贝叶斯优化算法对DKELM的超参数进行寻优,旨在提高DKELM的性能,更好地应用于实际故障诊断。
2 BO-DKLEM模型
目前,贝叶斯优化在求解黑盒函数问题中应用越来越广泛,已经成为超参数估计的主流方法[25-26]。区别于网格搜索方法和随机搜索方法,贝叶斯优化采用序贯的算法模型,通过选取参数点不断更新概率模型,在过去搜索结果的基础上获得当前的最优值。贝叶斯优化方法中主要包括两个组成部分:1)概率代理模型:概率代理模型描述了目标函数的历史结果,每一次迭代过程概率代理模型根据当前数据点的目标函数结果进行改进,直至找到符合要求的结果或者达到最大迭代次数。概率代理模型用来代理描述目标函数,对数据点集合和目标函数值进行统计分析;2)采集函数:BO通过将概率代理模型代入采集函数中计算极值,估计当前情况下最优数据点最有可能出现的一些位置,并将其作为选择下一组需要计算的数据点。下面从概率代理模型和采集函数两个方面介绍BO的基本原理。
2.1 概率代理模型
由于优化目标函数可能不存在显式的函数表达式,因此BO采用概率代理模型对目标函数进行近似表示。基于初始采样数据点开始构建初步的概率代理模型,随着数据点信息量的增加,逐步对概率代理模型进行修正和更新。概率代理模型一般分为参数模型和非参数模型两种。目前高斯过程(GP,gaussian process)回归作为概率代理模型取得了较好的应用。高斯过程回归属于非参数模型,其每个有限子集都服从多元正态分布,通过使用高斯过程的先验信息进行回归分析。高斯过程是多元高斯分布向无穷维的扩展,由均值函数和协方差函数组成:
f(x)~GP(m(x),k(x,x′))
(19)
其中:f(x)为目标函数;m(x)为均值函数;k(x,x′)为协方差函数矩阵。在第t次试验后,可以获得数据点集合{x1:t,f1:t},由于高斯过程上任意点ft+1与之前的观测数据服从联合高斯分布,进一步可以得到预测分布:
(20)
对于均值和协方差函数的推导和具体形式本文不再赘述。根据式(20),则可以根据高斯过程的后验分布对未知函数f(x)在任意位置的值和所在位置的均值、方差做出估计。
2.2 采集函数
直接从概率代理模型中随机选择数据点寻找最优解通常需要耗费大量的时间。BO采集函数在每次迭代过程中获得下一个采样数据点。采集函数根据已经观测到的数据更新的后验概率分布进行构造,下一个评估的采样数据点通过最大化后验概率分布进行选择,即:
xt+1=argmaxαt(x;D)
(21)
常见的采集函数包括概率提升函数(PI,probability of improvement)、期望提升函数(EI,expected improvement)以及上置信边界函数(UCB,upper confidence bound)等。由于本文使用高斯过程作为概率代理模型,其后验概率分布预测中包括均值和方差,因此通过使用代理模型计算得到预测分布中均值和方差的关系,使采集函数最大化,以此来估计最优的下一个采样结构点xt+1:
αUCB(x)=μ(x)+γσ(x)
(22)
其中:γ为调节参数,采集函数通过γ控制对探索未知和已知数据信息之间的平衡。
2.3 BO-DKLEM模型训练过程
BO-DKELM模型的训练过程如图5所示。

图5 BO-DKELM故障诊断模型训练过程
在图5中,贝叶斯优化的目标函数设计为分类错误率,优化目标为在超参数空间内寻找到一组超参数组合x={nλ,C1,C2,δ},使得训练集和验证集的错误率之和最低:
ξ=argmin2-Acct-Accv
(23)
其中:Acct为训练集的准确率;Accv为验证集的准确率。此时可确定概率代理模型的输入为数据点集合{x1:t,ξ1:t},输出为超参数与目标函数之间的函数关系f(x)。基于BO-DKELM模型的故障诊断流程可以分为4部分:
1)将采样数据划分为训练集、验证集和测试集;
2)构建DKELM模型,确定网络层数、ELM-AE采用的激活函数、KELM采用的核函数;
3)训练BO-DKELM模型,输出DKELM模型中各隐层的节点个数、ELM-AE的正则化系数、KELM的正则化系数和核参数,构建BO-DKELM模型;
4)通过测试数据集验证所构建模型的故障分类性能。
3 案例验证
为了验证所提方法的可行性和有效性,本文采用凯斯西储大学实验室的实验数据,实验设施如图6所示[27]。

图6 故障实验设施
电机作为整套系统的动力源,驱动滚动轴承旋转带动负载工作;功测机用于模拟测试平台的负载,其实际输出扭矩可根据测试需求进行调节,并通过扭矩传感器进行测量;利用加速度作为振动传感器,通过测量加速度对振动强度进行估计;各种不同故障类型的滚动轴承用于模拟实际生产中的滚动轴承故障。故障位置主要包括滚珠缺陷、外圈缺陷和内圈缺陷。轴承的故障由电加工产生,故障尺寸为7、14和21 mil。每一种故障都有上述的3种损伤情况,代表着不同严重程度的故障,因此一共有10种不同的轴承健康状况数据,包括正常情况的轴承和不同严重程度的故障情况。具体信息列于表1中。

表1 故障信息表
将样本的数据点设置为1 024,将测试信号作为BO-DKELM的输入。对于每个类别的样本,从原始振动信号中随机构建250个样本,因此构建了含有2 500个样本的样本集,设置训练集:验证集:测试集的比例为7∶2∶1。设置ELM-AE单元个数为2个,其中激活函数选用sigmoid函数。其中:ELM-AE单元的节点数n1和n2的搜索范围设置为[0,200],ELM-AE的正则化系数C2、KELM中正则化系数C1和核参数δ的搜索范围统一设置为[0.001,1 000],最大搜索次数设置为20次,最小目标值搜索过程和故障诊断结果如图7和图8所示。
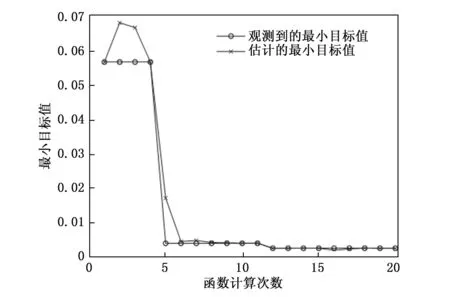
图7 最小目标值搜索过程

图8 基于BO-DKELM的故障诊断结果
从仿真结果可以看出:1)BO-DKELM算法在第12次迭代时结果收敛,训练集与测试集的错误率之和最低为0.25%;2)经过20次搜索后,贝叶斯优化算法给出了模型的最优超参数分别为:n1=199、n2=159、C1=539.205 0、C2=622.172 6、δ=38.807 9;3)BO-DKELM算法的测试集分类正确率为99.60%,F1得分为0.996 4。
为说明本文方法的优越性,将本文所提BO-DKELM故障诊断模型与DKELM、KELM和ELM等模型进行对比,各模型的激活函数都选择为Sigmoid函数,表2给出了算法其余超参数具体数值。

表2 模型超参数设置
所有模型所用的故障数据集相同。一共进行了20次实验,取20次实验结果的平均值,最终故障诊断结果对比如表3所示。

表3 故障诊断结果对比
可见,基于BO-DKELM的诊断模型相比于DKELM、KELM和ELM,测试集准确率分别提高了5.06%、15.86%和20.02%,F1得分分别提高了0.050 5,0.123 0和0.193 2。进一步将本文所提方法与CNN、2D-CNN[28]、DBN[29]、CNN+2D-CNN进行比较,这些方法的详细描述如下:
1)CNN包括一个输入层,两个一维卷积层(卷积规模分别为1×6和6×16),两个池化层,一个全连接层,一个softmax分类器和一个输出层,卷积层和池化层的核尺寸分别为5、6、3、6。
2)由于原始信号数据的维度为1 024,将原始信号数据转化为32*32维的矩阵作为2D-CNN的输入。2D-CNN包括一个输入层,两个一维卷积层(卷积规模分别为3×6和6×16),两个池化层,一个全连接层,一个softmax分类器和一个输出层,卷积层和池化层的核尺寸分别为3、2、2、2。
3)DBN中包含一个输入层,两个隐含层和一个输出层,网络结构为[1 024,50,20,10],学习率为0.05,小批量尺寸为8,迭代次数为500。
4)CNN+2D-CNN通过特征融合层将CNN和2D-CNN两个通道全连接层的特征进行拼接。设置SVM为分类器,选取核函数为高斯核,核参数为0.01,惩罚因子为1。学习率设置为0.005,小批量尺寸设置为8,总迭代次数为500,损失函数为交叉熵。这些方法在样本集上的故障诊断准确率和F1得分如表4所示、可以看出,本文所提出的BO-DKLEM故障诊断能力更强,在这些模型中,DBN获得的故障诊断准确率和F1得分的值最低,与其余方法结果相比,由于本文所提出的BO-DKELM故障诊断模型通过贝叶斯优化使得模型的超参数达到最优,能够有效提高系统的故障诊断能力,上述结果验证了本文所提方法的优越性。

表4 与现有故障诊断结果方法对比
4 结束语
本文提出了一种基于BO-DKLEM的故障诊断方法。通过贝叶斯优化算法对DKELM中的隐含层节点个数、正则化参数和核宽度进行优化,构建BO-DKELM模型,然后利用数据集对优化后的DKELM模型进行训练。通过故障诊断结果可以看出,本文所提方法能够得到最优的超参数,相比于未优化的DKELM算法和传统的ELM、KELM等算法,本文所提方法可以有效提高滚动轴承故障诊断的准确性。然而本文所提方法需要利用优化算法对超参数进行寻优,因此诊断时间有所增加。如何在保证故障诊断具有较高准确性的前提下进一步缩短诊断时间,是下一步研究的主要内容。

