基于修正割线方程的BB梯度法

摘 要：将修正的割线方程和BB梯度法结合起来，从而得到一类修正的BB步长，再利用Zhang-Hager非单调线搜索，提出一个改进的BB梯度方法（MB法）。在一定的假设下，MB法是具有全局收敛性的。同时对MB法和同类型的几个BB方法进行大量的数值试验，结果表明MB法的数值效果是最好的。

关键词：Barzilai-Borwein梯度法；非单调线搜索；无约束优化；改进割线方程

中图分类号：O224   文献标识码：A文章编号：1674-0033（2024）02-0022-04

引用格式：杨爽艺.基于修正割线方程的BB梯度法[J].商洛学院学报，2024，38（2）：22-25.

BB Gradient Method Based on Modified Secant Equation

YANG Shuang-yi

（College of Mathematical Sciences， Chongqing Normal University， Shapingba  401331， Chongqing）

Abstract： A modified BB gradient method （MB method） is proposed by combining the modified secant equation with the BB gradient method， thus obtaining a class of modified BB steps， and then using Zhang-Hager nonmonotonic line search. Under certain assumptions， the MB method is globally convergent. A large number of numerical experiments are also conducted on the MB method and several BB methods of the same type， and the results show that the MB method is the best numerically.

Key words： Barzilai-Borwein gradient method; nonmonotone line search; unconstrained optimization; modified secant equation

對于求解无约束优化问题：

f（x）    （1）

其中，f（x）：Rn→R为连续可微函数，n是变量的个数，x为决策变量。梯度法是解决这类问题最简单的方法之一，其迭代格式为：

xk+1=xk-αkgk    （2）

其中，gk是f在xk处的梯度，αk是步长，不同的步长对应着不同的梯度法。

文献[1]在最小二乘意义下去近似标准割线方程Bksk-1=yk-1和Hkyk-1=sk-1中的Bk和Hk，得到步长的两个表达式：

[αBB1][k]=

（3）

[αBB2][k]=

其中，sk-1=xk-xk-1，yk-1=gk-gk-1。

[αBB1][k]和[αBB2][k]被称为两点步长或者BB步长，对应的梯度法被称为BB梯度法，简称BB法。BB法拥有更快的收敛速度，同时还避免了一些复杂的计算。BB法的良好性能激起了研究者对BB法的研究。文献[2]估计迭代点的单纯形梯度，对BB法进行改进。文献[3]利用循环策略去更新BB步长。尽管许多研究者提出了一些改进的BB法，但对最优的BB梯度法还未达成共识。文献[4]基于文献[5]提出的割线方程，推导出了6个修正的BB步长。文献[6]基于文献[7]提出的修正割线方程，并提出了改进BB步长。这些方法都表明，从割线方程角度去修正的BB法是可行的，但是数值性能上还存在一定缺陷。基于此，本文在文献[8]的研究基础上，进一步优化，结合一个具有更好性质的割线方程来修正BB法。

1  修正的BB梯度法（MB）的算法

在文献[9]中，令f（x）的Hessian矩阵Q（xk）取近似Bk和Bk+1，从而提出一个改进的割线方程：

Bksk-1=wk-1=2yk-1+uk-1       （4）

其中，uk-1=gk。

将这个割线方程和BB法结合起来，用wk-1代替原BB1步长中的yk-1，则得到一个新的步长：

[αMB][k]=        （5）

其中，sk-1=xk-xk-1，yk-1=gk-gk-1。

基于文献[10]中的算法框架，提出了一个修正的BB型算法（MB法）。

选择初始步长后，利用Zhang-Hager非单调线搜索[11]来计算后面的近似步长。

步骤1  给定初始值x0∈Rn，λmax≥λmin≥0，ε，γ∈（0，1），ηk∈[0，1]，0<σ1<σ2<1；计算f0，令C0=f0，Q0=1，α0=1，k=0。

步骤2  若‖gk‖∞≤ε，停止迭代；否则，令dk=-αkgk。

步骤3  计算步长αk（非单调线搜索）。

先令t=1，若满足：

f（xk+αkdk）≤Ck+γtαkg[k][T]dk       （6）

再令xk+1=xk+tαkdk，转向步骤4。否则，选择t∈[σ1t，σ2t]，转向步骤2。

步骤4  用式（5）和式（6）计算步长，若αk<0，则令αk=λmax。否则，令αk=min{λmax，max{λmin，αk}}，转向步骤5。

步骤5  选择ηk∈[ηmin，ηmax]，并计算：

Qk+1=ηkQk+1，Ck+1=。

步骤6  令k=k+1，转向步骤2。

2  收敛性分析

假设1  水平集Ω={x∈R：f（x）≤f（x0）}有界，即存在一个常数M>0，有：

‖x‖≤M，?x∈Ω        （7）

假设2  目标函数f在Ω的某个邻域N连续可微，且梯度▽f Lipschitz连续，即存在常数L>0，有：

‖g（x）-g（x*）‖≤L‖x-x*‖， ?x，x*∈N        （8）

引理1  设Ak是关于k的平均函数值，即Ak=fi。如果对于任意k都满足▽f（xk）dk≤0，那么在第k次迭代过程中，对任意的ηk，都有fk≤Ck≤Ak。

证明：令Dk（t）=             （9）                                                     其中，D：R→R。

求导可得：

D[′][k]（t）=                        （10）                                         由于fk≤Ck-1，所以对任意的t≥0，都有D[′][k]（t）≥0，即Dk（t）是单调递增的。

故有：

fk=Dk（0）≤Ck                      （11）                                            即Ck有下界，然后用归纳法证明Ck有上界。

当k=0时，有C0=f（x0）成立。

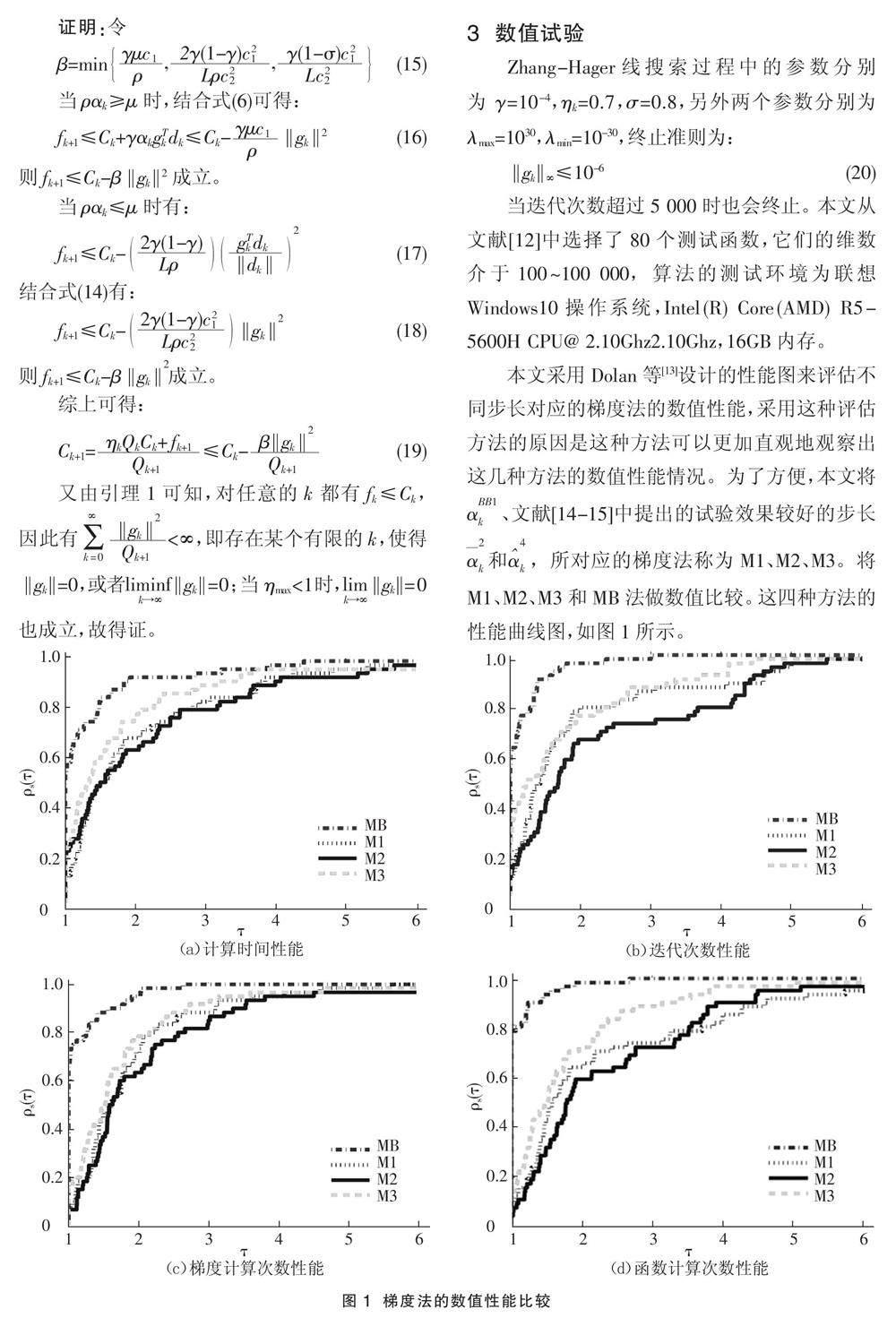
现假设对任意的0≤j

Qj+1=1+ηj-m≤j+2               （12）                                            又由于Dk（t）是单调递增的，则有：

Ck=Dk（Qk-1）≤Dk（k）=≤=Ak （13）

结合式（11）和式（13）可得fk≤Ck≤Ak，故得证。

进一步，在[αmin，αmax]中选择步长αk，则存在两个常数c1和c2，使得搜索方向dk满足：

g[k][T]dk≤-c1‖gk‖2，‖dk‖≤c2‖gk‖，?k∈R （14）

定理1  在假设1和假设2条件下，设MB法产生的迭代点列为{xk}，那么就存在某个有限的k，使得‖gk‖=0，或者‖gk ‖=0。进一步，当ηmax<1时，有‖gk‖=0。因此，迭代的每个收敛子序列都会接近一个点x*，其中▽f（x*）=0。

證明：令

β=min

，

，

（15）

当ραk≥μ时，结合式（6）可得：

fk+1≤Ck+γαkg[k][T]dk≤Ck-‖gk ‖2（16）

则fk+1≤Ck-β‖gk ‖2成立。

当ραk≤μ时有：

fk+1≤Ck-

（17）

结合式（14）有：

fk+1≤Ck-

‖gk ‖（18）

则fk+1≤Ck-β‖gk ‖成立。

綜上可得：

Ck+1=≤Ck-   （19）

又由引理1可知，对任意的k都有fk≤Ck，因此有<∞，即存在某个有限的k，使得‖gk‖=0，或者‖gk‖=0；当ηmax<1时，‖gk‖=0

也成立，故得证。

3  数值试验

Zhang-Hager线搜索过程中的参数分别为γ=10-4，ηk=0.7，σ=0.8，另外两个参数分别为λmax=1030，λmin=10-30，终止准则为：

‖gk ‖∞≤10-6（20）

当迭代次数超过5 000时也会终止。本文从文献[12]中选择了80个测试函数，它们的维数介于100～100 000，算法的测试环境为联想Windows10操作系统，Intel（R） Core（AMD） R5-5600H CPU@ 2.10Ghz2.10Ghz，16GB内存。

本文采用Dolan等[13]设计的性能图来评估不同步长对应的梯度法的数值性能，采用这种评估方法的原因是这种方法可以更加直观地观察出这几种方法的数值性能情况。为了方便，本文将α、文献[14-15]中提出的试验效果较好的步长和，所对应的梯度法称为M1、M2、M3。将M1、M2、M3和MB法做数值比较。这四种方法的性能曲线图，如图1所示。

数值试验通过求解大量问题，将四种梯度法从计算时间、迭代次数、梯度计算次数和函数计算次数四个维度进行比较。图1（a）是对四种梯度法的计算时间的比较，发现MB法解决问题花费的计算时间最少。图1（b）是对四种梯度法的迭代次数的比较，发现MB法迭代次数最少。图1（c）是对四种梯度法的梯度计算次数的比较，发现MB法的梯度计算次数最少。图1（d）对四种梯度法的函数计算次数的比较，发现MB法的函数计算次数最少。

从图1可见，在计算时间、迭代次数、梯度计算次数和函数计算次数上看，MB法始终表现得最好，这就说明，MB法具有比较好的数值效果。

4  结语

将改进割线方程和BB梯度法结合起来，得到一个新的步长——MB步长，再结合非单调线搜索得到MB法。通常的步长只使用了当前迭代点和上一迭代点的值及梯度值，但是MB步长还使用了当前迭代点和上一迭代点的函数值，因此充分利用了迭代点的信息。通过收敛性分析得到MB法是全局收敛的，并且不需要对目标函数作任何的凸性假设。数值试验结果表明，从时间、迭代次数、函数计算次数和梯度计算次数上来看，MB法都具有较好的计算效率。

参考文献：

[1]  JONATHAN B， BORWEIN J M. Two point step-size methods[J].Ima Journal on Numerical Analysis，1988（1）：1.

[2]  郑鹏远，李琴，孙忠林.基于Barzilai-Borwein梯度法的多微电网系统递阶优化调度算法[J].科学技术与工程，2020，20（30）：12443-12451.

[3]  杨奕涵.带有循环策略的自适应截断BB梯度法研究[J].黑龙江科学，2023，14（20）：54-57.

[4]  BABAIE-KAFAK S， FATEMI M. A modified two-point stepsize gradient algorithm for unconstrained minimization[J].Optimization Methods and Software，2013，28（5）：1040-1050.

[5]  LI D H， FUKUSHIMA M. A modified BFGS method and its global convergence in nonconvex minimization[J].Journal of Computational and Applied Mathematics，2001，129（1-2）：15-35.

[6]  郑燏涛.Barzilai-Borwein梯度法及其在优化算法中的应用[D].兰州：兰州大学，2018：11-24.

[7]  FORD J A， MOGHRABI I A. Multi-step quasi-Newton methods for optimization[J].Journal of Computational and Mathematics，1994，50（93）：305-323.

[8]  陈旦.基于混合割线方程修正的BB梯度法[J].绵阳师范学院学报，2023，42（2）：8-14.

[9]  HASSAN B A， MOGHRABI I A R. A modified secant equation quasi-Newton method for unconstrained optimization[J].Journal of Applied Mathematics and Computing，2023，69：451-464.

[10] BIGLARI F， SOLIMANPUR M. Scaling on the spectral gradient method[J].Journal of Optimization Theory and Applications，2013，158（2）：626-635.

[11] HAGER W W， ZHANG H. A new conjugate gradient method with guaranteed descent and an efficient line search[J].SIAM Journal on Optimization，2005，16（1）：170-192.

[12] GOULD N I M， ORBAN D， TOINT P L. CUTEr and SifDec： a constained and unconstrained testing environment， revisited[J].Acm Trainscations on

Mathematical Software，2003，29（4）：373-394.

[13] DOLAN E， MOR? J J. Benchmarking optimization software with performance profiles[J].Mathematical Programming，2001，91：201-213.

[14] XIAO Y， WANG Q， WANG D. Notes on the Dai-Yuan-Yuan modified spectral gradient method[J].Journal of Computational and Applied Mathematics，2010，234（10）：2986-2992.

[15] ZHANG J Z， DENG N Y， CHEN L H. New quasi-newton equation and related methods for unconstrained optimization[J].Journal of Optimization Theory and Applications，1999，102（1）：147-167.