基于GRA-ISM-HMM的广州市肉及肉制品安全风险评估

张维蔚，陈坤才＊，张玉华，陈燕珊，黄德演

（1.广州市疾病预防控制中心，广东广州 510440）（2.广州大学经济与统计学院，广东广州 510006）（3.广东毓秀科技有限公司，广东广州 510623）

食品安全问题是影响国家发展的全球性的重要健康问题[1]。随着生产水平的提高，市场上的食品种类也越来越多，食品安全监管难度也随之增大。食品安全事件仍时有发生，例如2018 年桂林学术交流会上500 余人餐后出现呕吐、腹泻、发烧等症状[3]和2021 年中央电视台曝光“养羊大县”青县“瘦肉精”羊肉事件，该县每年羊出栏量高达70 万只[4]等。由此可见，食品安全问题依旧是国家治理的一个重要方向。

在所有食品种类中，肉及肉制品是国民日常所需的重要食品种类之一，是食品安全的重要监管方向。相关数据显示，我国2015 至2020 年间食品日常监督管理抽检数据中，肉及肉制品不合格占比高达8.00%[5]。刘明等[6]还指出肉及肉制品在大型活动中，风险级别为中度风险。此外，肉及肉制品在我们日常饮食以及大型活动中被广泛食用，出现频次超高，是需要重点研究的食品种类。

在食品安全的风险评估方向上，研究者提出了多种研究方法。除了常规的描述性统计分析[7]外，比较经典的方法有蒙特卡罗法[8]、贝叶斯网络[9]和层次分析法[10]，其中蒙特卡罗法和贝叶斯网络分别为定量和定性评估，而层次分析法可以综合定性和定量评估。除此之外，Lin 等[10]尝试使用灰色关联分析（GRA）综合解释结构模型（ISM）来构建风险指数，该方法剖析了检测指标间的相关性并绘制了结构图，使得构建的风险指数更具客观性。上面方法实际上都是通过生成指标权重，继而得到风险指数，对食品安全进行评估，但这不能对风险趋势进行预测。因此结合数据时间特征及马尔可夫链假设，研究者们[11]尝试引入隐马尔可夫模型（HMM）对食品安全进行评估和预测，结果表明HMM 具有高准确性和强时效性。在隐马尔可夫模型研究中，估计隐状态数目一直是一个难点。在这方面，刘鹤飞等[14]利用可逆跳跃蒙特卡罗算法给了HMM 的隐状态数目的估计。Rousseeuw 等[15]使用谱聚类算法估计了离散状态HMM 的参数。在此背景下，Zheng等[16]综合了之前研究者的方法，根据观测状态首中时期望构建特征矩阵，再由奇异值分解以及K 均值聚类确定隐状态数目。

上述所阐述的方法已被应用到许多种类食品的研究，但鲜有应用到对于肉及肉制品的风险评估研究。鉴于此，本文针对广州食品安全监测数据关于肉及肉制品的检测数据，综合已有方法（即GRAISM-HMM），利用GRA 和ISM 构建风险指数，运用首中时期望特征矩阵对HMM 隐状态进行估计，从而对广州市肉及肉制品安全进行风险评估。

1 数据与方法

1.1 实验数据

本文数据来自广州食品安全监测2015 年至2021 年抽检的肉及肉制品数据，样品共806 份，检测目的是检测肉及肉制品中的化学污染物，检测方法按照原国标方法测定。检测项目受每年食品安全政策及民生食品安全关注焦点影响，每年都有所变动，每年具体抽检指标见表1 所示。

表1 2015年至2021年各年份检测指标表Table 1 Chemical detecting indicators from 2015 to 2021

在这些数据中，一些肉及肉制品种类具有不同的检测方案，需要分类处理，去除未超出检出限的指标，各年份肉及肉制品分别的检测指标见表2 所示。

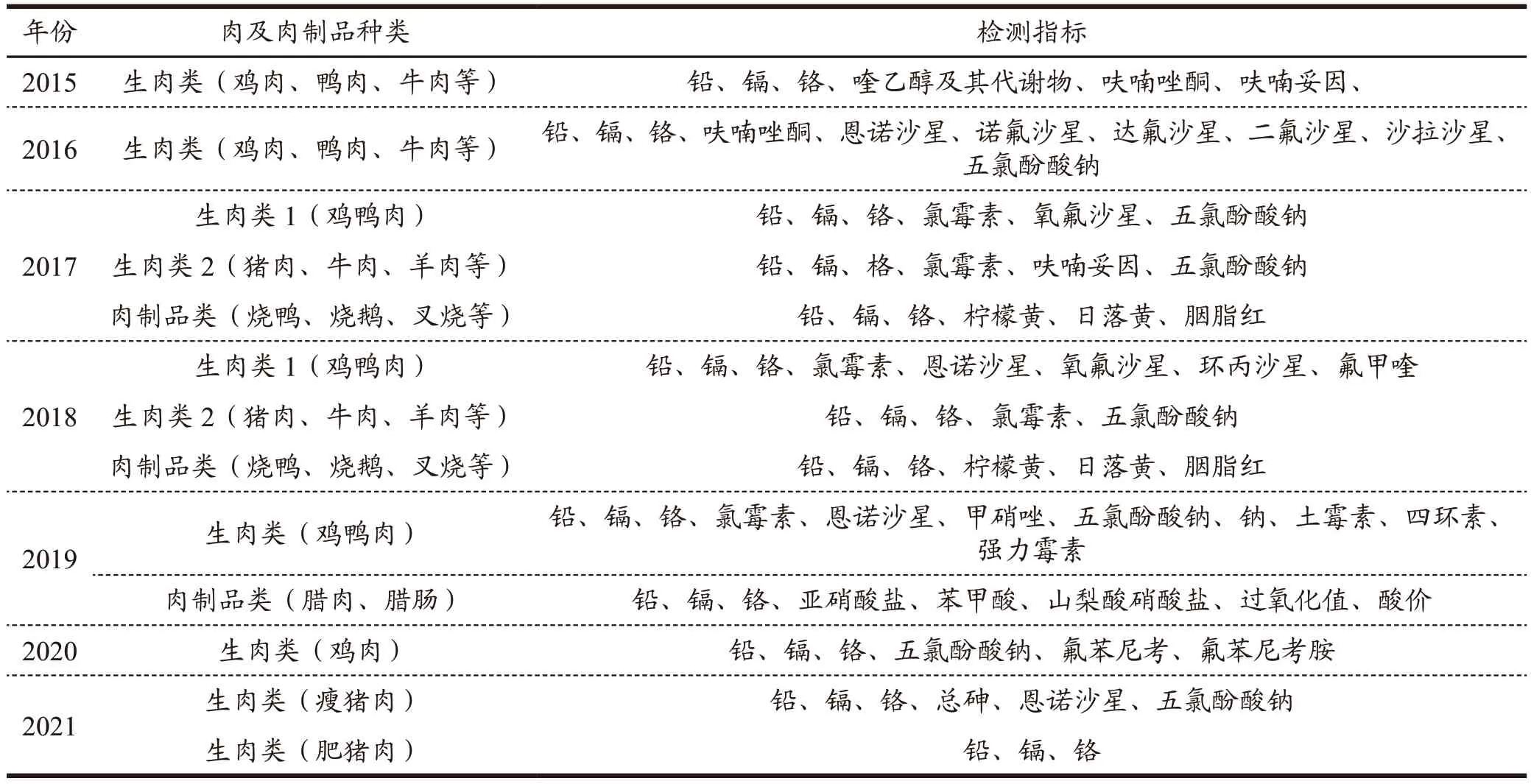
表2 2015至2021年不同肉及肉制品种类的有效检测指标Table 2 Effective detection indicators for different meat and meat product types from 2015 to 2021

1.2 实验环境

本研究基于Python 3.7.6 环境构建模型，实验设备为Windows 11 笔记本电脑，Intel(R) Core™ i5-11400H 处理器，NVIDIA GeForce RTX 3050 显示适配器，16 G（3 200 MHz）内存。

1.3 实验方法

1.3.1 灰色关联模型

灰色关联模型（GRA 模型）是一种多元分析方法，其原理是根据不同序列的曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近，相应序列之间的关联度就越大，反之则越小。

首先设定待确定关联度的两个序列分别为比较序列X=（x1，x2，…xp）’和参考序列Y=（y1，y2，…yp）’，其中x1，x2，…xp，y1，y2，…yp分别为各因子，其样本量均为n。由于各因子量纲不同，通常先进行初值化处理。

式中：

xi（j）′——第i 个比较序列因子xi的第j 个样本初值化结果；

xi（j）——第i 个比较序列因子xi的第j 个样本；

yk（j）′——第k 个比较序列因子yk的第j 个样本初值化结果；

yk（j）——第k 个比较序列因子yk的第j 个样本。

接下来求解序列差异矩阵δ以及矩阵最大值δikmax和最小值δikmin，具体公式如下：

最后，对第j 个样本，求解xi与yk的关联系数Yik以及X 和Y 的关联度矩阵C=(Cik)p×q，公式如下：

式中：

Cik——xi与yk的关联度，关联度值越大，则xi对yk的影响程度越大。

1.3.2 解释结构模型

解释结构模型（ISM）是一种用于分析复杂系统层级结构的模型方法，该方法常用于将影响目标变量的各因素进行分层处理。方法步骤如下：

（1）构建影响因素的影响矩阵A，即邻接矩阵。邻接矩阵元素为“0”或“1”，其中“1”表示两因素之间有直接连接关系。如果由相关性构建，“1”通常表示为强相关，否则为“0”。

（2）构建可达矩阵M。首先将邻接矩阵A与单位矩阵E相加，然后进行n 次布尔运算，即当满足(A+E)n-1≠(A+E)n=(A+E)n+1停止运算，由此得到可达矩阵M=(A+E)n。其中可达矩阵第i 行第j 列元素Mij为“1”表示影响因素i 与影响因素j 之间存在路径，否则表示不存在路径。

（3）构建可达集R、先行集Q 与它们的交集B。可达集表示为M 中某影响因素对应行中，元素为1的因素集合。先行集表示为M 中某影响因素对应列中，元素为1 的因素集合。

（4）构建相关层次。首先确定第一层因素，即可达集只有本身的影响因素，然后删除该列，再次搜索可达集只有本身的影响因素放入第二层，直至最后一个因素被剔除。

ISM 用分层结构显式地展现了各影响因素的关系，为对各因素赋予权重提供了有效的依据。

1.3.3 隐马尔可夫模型

隐马尔可夫模型（HMM）是经典的概率统计模型，包含马尔可夫链和一般随机过程。它描述的是由隐藏的马尔可夫链以一定概率生成状态序列，再由状态序列以一定概率随机生成观测序列的过程，图像表示如下：

图1 隐马尔可夫模型图Fig.1 Hidden Markov model

其中｛O1,O2,…,OT｝表示不同时刻的观测序列，｛q1,q2,…,qT｝表示不同时刻的隐藏状态序列。隐状态之间能够相互转换，但其不能被观测，隐状态以一定概率生成观测序列使得我们能观测到，因此HMM 的一个重要任务就是去求解这些转换概率。若观测也是离散状态，先假设共有N个隐藏状态｛R1,R2,…,RN｝，共有M 类离散观测｛u1,u2,…uM｝，则模型参数可以由λ=(π,Λ,B)表示，其中π=(π1,π2,…πN)表示初始时刻的状态分布概率矩阵，Λ=(αij)N×N表示隐状态之间的转移概率矩阵，其中aij=P(qt+1=Rj|qt=Ri),1≤i≤N,1≤j≤N,表示任意t时刻隐藏状态为Ri时，下一时刻转换成Rj的概率。B 表示隐状态对于观测的发射矩阵，bij=P(ot+1=uj|qt=Ri),1≤j≤M,1≤i≤N表示任意t时刻隐状态为Ri时，观测状态为uj的概率。

在估计相关概率前，需要先确定隐状态的数目N。如果两个观测状态ui和uj是来自同一个隐状态，那么ui到某个固定点的首中时（即首次命中时间）与uj到这个固定点的首中时分布相同。基于以上事实，有这样一个定理：假设HMM 的转移概率矩阵是遍历的，若首中时期望矩阵有s个非零特征值，则该HMM 模型有s个隐状态。这是由于若有两个观测状态属于同一个隐状态，那它们所在的首中时期望矩阵行之间存在相关性，因此会存在0 特征值，所以非零特征值对应隐状态个数。参照Zheng等[16]所提出的估计算法，得到隐状态数估计算法如表3 所示。Zheng 等[16]还对首中时期望均值进行聚类分析来获得隐状态数目，但本文观测状态并不多，无需进行聚类分析，所以运用表3 的算法。

表3 HMM隐状态数估计算法Table 3 Estimation algorithm of hidden states’ number of HMM

估计隐状态数后，便可以HMM 建模。HMM主要解决三类问题：

（1）评估问题：当给定观测序列O=｛O1,O2,…,OT｝和已知模型参数λ时，计算P(O|λ)，即计算参数λ下，该观测序列O被观测到的概率。

（2）解码问题：当观测序列和模型参数已知情况，计算最大可能出现的隐藏状态序列。

（3）学习问题：已知观测序列，求解模型参数λ使得P(O|λ)最大。

1.3.4 GRA-ISM-HMM联合模型

该节阐述对以上三种模型的连接操作。首先通过灰色关联分析可以得到各影响因素的相互影响程度，在本文指代各检测指标相互之间的关联度。设定阈值为0.9[17]，当关联度超过阈值，判定这两个检测指标之间有连接关系，进而可以得到ISM 的邻接矩阵。但在实验中发现大多数检测指标关联度都非常大，这导致根据原ISM 的分层困难，因此在参考经典ISM 的同时，增加一个条件即随着分层结构箭头指向，关联度应逐级递减。增加该条件后，便可以得到分层结果，由此我们可以逐级赋予权重，权重逐级递减，从而得到各年份的风险指数。采用分位数四分法对风险指数进行分级，可以得到离散观测状态，接着再使用HMM 便可以得到观测下各年份隐藏的风险等级情况，具体流程图如图2 所示。

图2 GAR-ISM-HMM 流程图Fig.2 GAR-ISM-HMM flow chart

2 结果与分析

由于数据量纲不同，对数据进行归一化处理后进行灰色关联分析。若某指标所有检测结果都低于检出限，归一化后便都为0，应不进行灰色关联分析。以2015 年为例，有效检测指标为铅、镉、铬、喹乙醇及其代谢物、呋喃唑酮、呋喃妥因六个，得到的灰色关联矩阵结果如图3 所示。

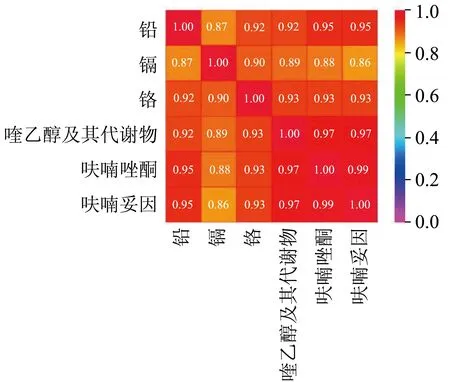
图3 2015 年灰色关联分析结果图Fig.3 Results of grey correlation analysis in 2015

根据灰色关联度矩阵，可以利用ISM 构建分层结果，得到分层结构图如图4 所示，以2015 年为例。

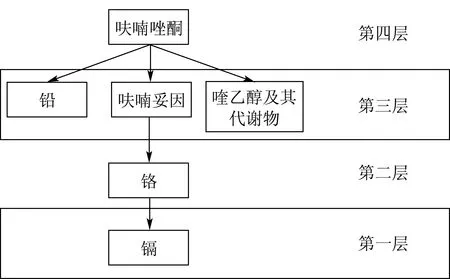
图4 2015 年分层结构图Fig.4 Hierarchical structurein 2015

表4 2015年各指标权重表Table 4 Weights of each indicator in 2015

根据赋予的权重便可得到各年份加权综合风险指数。各年份风险指数结果如图5 所示。

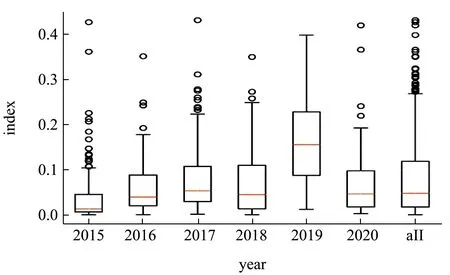
图5 2015-2020 年份综合风险指数图Fig.5 Composite risk index from 2015 to 2020

图5 中“all”是所有年份风险指数数据的汇总，用来观察所有样本的数据分布情况。由于使用归一化处理，且每年各指标权重和为1，因此如果一个样本各指标数值都很大的情况下，加权综合风险指数会越接近1。也就是说，数值“1”可作为风险指数结果参考顶点。首先从图5 可以看出，所有样本的风险指数都未超过0.5，且大多数样本风险指数不超过0.2，由此可得广州每年的肉及肉制品安全处于较低的风险水平，但依旧有极少样本风险较高，关乎健康安全，这些样本也需要重点关注。其次，从图5 可以明显看出，2019 年加权综合风险指数相对明显较高。但由于广州肉及肉制品生化检测还在逐步完善的过程，每年检测指标变动较大，且检测样本种类也有改变。所以，2019 年风险指数高的原因需要进一步探讨。探讨前我们可以先根据HMM模型探索该观测下各年份的隐藏状态，观察隐藏风险状态与观测是否一致。

在进行离散HMM 建模前，需要先将得到的风险指数划分风险等级，根据样本特点，在这里采用分位数划分法。因为存在相对异常高的风险指数样本，所以传统的5-标度法（5 等分）并不能很好的划分风险等级，而且分位数划分法能够使得各样本落入各等级的概率相对均等。对5-分位数划分、4-分位数划分和3-分位数划分结果进行比较，最终选择4-分位数划分，即划分为四个等级。最终划分结果如表5 所示。

表5 风险等级划分表Table 5 Risk classification

由于HMM 的离散观测从“0”开始，表5 将第1 个等级划分为“0”。根据表5 的风险等级以及各年份平均风险指数，2015 年至2020 年六年的观测状态序列为 [122231]。

得到观测序列后，开始估计HMM 隐状态数目。计算各个观测状态的之间的首中时，得到矩阵如下：

矩阵（8）中“∞”表示两种状态相互转换概率为0。显然矩阵（8）含非0 特征值3 个，因此隐状态个数应取3 个为宜。

对HMM 模型进行多次训练，取得分最高的参数估计结果，结果如下所示：

π、Λ、B的概率都为四舍五入后的概率，如矩阵中的“0”实际结果均＜0.000 1，“1”实际结果均＞0.999 9，为了方便记录，矩阵里记为“0”和“1”，从矩阵B 可以得到观测状态与隐状态的明显对应关系，即隐状态“0”对应观测状态“2”，隐状态“1”对应观测状态“1”，隐状态“2”对应观测状态“3”。对得到的最高概率隐状态序列 [1 0 0 0 2 1]进行重新排级，可以得到隐藏的风险等级为 [0 1 1 1 2 0]。从中可以看出2019 年的风险确实相对较高，但2020 隐藏风险等级为“0”，且结果显示2021 的风险等级较大的概率往风险等级“1”转换，风险等级“1”为中等风险，对应观测状态“2”，即预测2021 年的风险指数均值大概率落在 [0.047 8,0.118 3]之间。因此可以认为广州肉及肉制品风险预测趋势良好。

利用网络爬虫采集外籍人才的网络招聘信息，进行探索性调查。对大量招聘信息进行文本挖掘，整理出有用的信息，为企业问卷设计和抽样提供依据。

为了验证这一结果，我们同样利用GRA-ISM 模型求解2021 年的综合风险指数，得到2021 年综合肉及肉制品综合风险指数的箱线图结果如图6 所示。

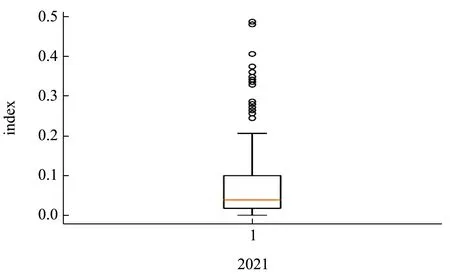
图6 2021 年综合风险指数图Fig.6 Composite risk index in 2021

从图6 中可以2021 年肉及肉制品的所有样本的综合风险指数大多分布在 [0,0.1]之间，总体风险较低。另一方面，对于各年份观测到的风险等级，我们以平均风险指数划分，因此求解2021 年平均风险指数，得到结果约为0.090 0，在 [0.047 8,0.118 3)内。根据表5 可得，2021 年风险等级为“2”即观测状态“2”，与HMM 预测结果一致。

上文也说到各年份检测指标变动较大，检测种类也有所变化，所以我们也应该重点探讨2019 年为何风险提升，是否当前检测策略需要提升。下面对2019 年风险指数较高进行逐一分析。首先，2019 检测指标较多，较多的危害指标可能导致风险指数增加，因此考虑采取相同检测指标对各年份进行分析。根据分析数据可得，各年份都检测的指标有金属污染物指标，即铅、镉、铬三个指标。根据前面分析的ISM 结构模型，设定三个指标权重分别为 [0.36,0.31,0.33]。最终各年份的风险指数图如图7 所示。

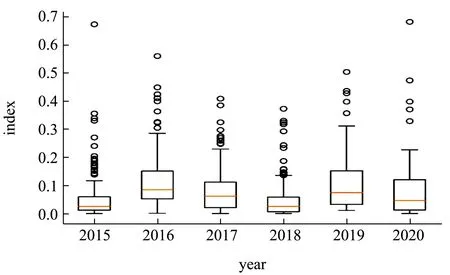
图7 2015～2020 年份重金属污染风险指数图Fig.7 Heavy metal pollution risk index from 2015 to 2020

从图7 中可以看出，2019 年金属污染物风险指数依旧较高，但相对综合风险指数，各年份风险相对有所变化，2019 年与各年份风险指数差异变小，即可以认为风险指数变动与检测指标变动有一定因果关系，但还有其他因素影响。然而，从另一方面讲，这也说明这几年对风险检测指标的探索是正确的，适当增加检测指标能更好挖掘安全风险。此外，2018 年重金属化学污染风险较小，但综合风险较大。

前文也说到各年份的检测种类也有所变化。现对数据中的包装形式、采样地点、产地、肉及肉制品分类等进行分析，发现2019 年肉及肉制品检测分类与其他年份相比有较明显的差异，2019 年检测的肉及肉制品分类增加了腊肉、腊肠两个分类。因此，我们有理由怀疑肉及肉制品种类是影响肉制品风险变动的原因之一，对各分类的风险指数进行均值和方差计算，得到结果如表6 所示。

表6 各肉制品分类风险指数均值与方差表Table 6 Sample mean and sample variance of risk index for each meat product classification

从表6 可以看出各肉及肉制品分类的风险指数之间确实存在差异，其中腊肉、腊肠确实风险指数较高，这说明了2019 年增加腊肉、腊肠两个分类确实是风险指数增加的原因之一。而除了腊肉、腊肠，其中鸡肉的风险指数也较高，但鸡肉每年都是重点检测项目，不是年度差异的原因。

在现有对肉及肉制品的风险研究当中，国内外大多数研究都主要集中在对菌落类的研究[18]，对肉及肉制品中的化学风险物质研究较少，且多具体为对某一种类（例如鸡肉[20]）或某一类化学物质（例如亚硝胺[21]）的研究，并没有与本文类似的研究包括重金属、农药残留等综合化学风险物质的报道，但依旧有一些对比价值，具体对比研究如下。以2011 至2014 年全国肉及肉制品数据为例，Xin等[22]使用矩阵风险模型对全国肉及肉制品进行风险评估，最终得出：炖肉和肉干是风险较高的肉制品种类，而细菌数目（菌落总数、大肠杆菌组）和防腐剂（包括山梨酸、苯甲酸等）是主要风险项目。对比发现，本文研究得到腊肉、腊肠是主要风险较高的种类，与该文结果相对一致；而在风险检测项目上，从表1 可以看出，广州肉及肉制品监测在2018 到2019 年增加了防腐剂（包括山梨酸、苯甲酸等）的检测，但在2020 剔除了这类指标，这是由于我们的数据中，2018 年有卤肉、叉烧等种类，2019 年有腊肉、腊肠等种类，对这些腌制品种类，山梨酸、苯甲酸等为主要风险项目，而2020 年所收集数据为在鸡鸭肉生肉种类，因此剔除这类指标。这也说明了我们的数据尽管包含多种种类，但对这些种类的检测指标是具有针对性的。对于鸡肉类，刘峰等[23]通过高效液相色谱-串联质谱法和食品安全指数法，分析了2016～2020 年宁夏市售鸡肉和鸡蛋中兽药残留状况，结果发现宁夏鸡肉中兽药残留主要风险物质为强力霉素，总体来说，宁夏鸡肉和鸡蛋的风险较低，但存在一定的风险隐患，但该文未考虑鸡肉中兽药残留状况在不同年份的变动情况。而在本文中，我们主要研究不同年份肉及肉制品的综合风险情况。此外，广州每年检测指标有所变动，以强力霉素为例，见表1 可知广州监测数据只在2019 年鸡肉种类对其检测，样本少且只在一个时间段，难以分析，且2020 年剔除了强力霉素这个指标。究其原因，细化到具体数据可以发现2019 年只有一个样本的强力霉素检测结果异常，其数值为9.28，其他都为1，即广州从2019 年抽检样本分析认为强力霉素该指标不是影响风险的重要指标，这与宁夏数据分析结果有所差异，可能是地域差异导致。在腊肉分类上，通过收集我国某县城集贸市场和其周边5 个乡镇集市的腊肉样本数据，朱联旭等[24]分析了腊肉中铬（Cr）、铅（Pb）、汞（Hg）、砷（As）和镉（Cd）5 种重金属和苯并 [a]芘的含量在不同腊肉断面的分布规律，并对其进行风险评估，得出结论：食用腊肉不会因为重金属和苯并 [a]芘导致严重健康风险。本文对各年份肉及肉制品数据进行重金属风险评估，发现2019 年较其他年份的重金属风险差异小于综合风险差异，而2019 年增加了腊肉、腊肠种类，这也侧面验证了腊肉、腊肠的重金属风险较小，与朱联旭等[7]的结果不冲突。综上，本文研究结果与现有研究没有冲突。

3 结论

从2015 至2020 年，广州肉及肉制品化学污染物综合风险指数总体较低，得到的风险指数都在 [0,0.45]之间。其中，2019 年风险最高，但这与2019 年检测指标变化以及增加腊肉、腊肠两类肉制品有关。

HMM 结果显示广州2015～2020 年观测到的风险等级为与隐藏风险等级一致，同时也显示2019年风险异常。此外，HMM 预测显示广州肉及肉制品化学污染风险在往良好的态势发展。

从2015 至2020 年，与综合风险指数相比，肉及肉制品重金属化学污染物风险各年份间差异较小，且较综合风险指数有一定变化，特别是2018 年，重金属化学污染风险较小，但综合风险较大。这说明在2018 年，除重金属外其他检测指标对综合风险指数有较高影响。

不同肉及肉制品种类综合风险指数有一定差异，其中鸡肉、腊肉、腊肠风险相对较高，是需要重点关注的品类。

数据上，检测数据中含有较多未超过检出限的数据，这也显示了广州市场上肉及肉制品某些检测指标控制得不错。

广州肉及肉制品化学污染检测依旧有需要改进，例如，每年检测指标变动给风险评估带来难度，因而需要尽快从数据中获取信息，确立好良好的检测方案。再如每年检测种类也有所变动，则需要确定重点风险种类，利用有限的资源有策略地开展检测。另外，有些文献显示一些食品在不同季度有不同风险等级的情况[25]，因此在有能力的情况下可以对肉及肉制品也采集不同季度的样本进行比较。

文章结论虽然基于广州市的检测数据，但同样可以给其他省市肉及肉制品监管和风险评估提供借鉴。人民日益增长的美好生活需要对食品安全也提出了更高的要求，需要更有力地监管和更精准的风险评估方法。