混合动力汽车发动机启停工况扭振自适应模糊控制

陈龙 陶磊

摘要：混合動力汽车（hybrid electric vehicle， HEV）发动机启停过程伴随的转矩脉动，易诱发车辆传动系扭振，导致车辆动力不平顺。为解决上述问题，提出并验证基于电磁阻尼自适应模糊控制的传动系扭振主动控制方法。建立行星混联式混合动力汽车发动机启停工况动力学仿真模型和发动机启停控制逻辑，提出发动机启停扭振自适应模糊控制策略，开展2种运行状态下发动机启停工况仿真，对比分析无控制和自适应模糊控制下传动系扭转振动响应曲线。结果表明，自适应模糊控制相比无控制状态：定置停车时发动机启动和停机工况扭振平均衰减率分别为23.8%和30.1%，车辆行进间发动机启动和停机工况扭振平均衰减率分别为12.1%和23.6%。该方法可有效衰减发动机启停工况传动系扭转振动，提升混合动力汽车发动机启停工况NVH（noise， vibration， and harshness）性能。

关键词：行星混联传动系；启停工况；扭转振动；主动控制；自适应模糊控制

中图分类号：TH113.2          文献标志码：A         文章编号：1000-582X（2024）01-104-11

Adaptive fuzzy control of torsional vibration of hybrid electric vehicle engine under start-stop condition

CHEN Long1，2， TAO lei1

（1. College of Mechanical and Vehicle Engineering， Taiyuan University of Technology， Taiyuan 030024， P. R. China; 2. State Key Laboratory of Automotive Simulation and Control， Jilin University， Changchun 130025， P. R. China）

Abstract： The starting and stopping process of a hybrid electric vehicle engine often results in torque ripple， leading to torsional vibrations in the vehicles powertrain system and causing irregular vehicle power delivery. To solve these problems， an active control method for torsional vibrations based on active control of electromagnetic damping torque of the motor is proposed. Firstly， a dynamic simulation model and engine start-stop control logic under engine start-stop condition is established. Additionally， an adaptive fuzzy control strategy for engine start-stop torsional vibration is proposed. Finally， the simulation model is used to simulate the engine starting and stopping conditions under two driving conditions of the vehicle. The torsional vibration response curves of the driveline under the proposed control method and without any control are compared and analyzed. The results show that the average torsional vibration attenuation rates achieved by the proposed method are 23.8% and 30.1%， respectively， during stationary stop engine conditions， compared to the uncontrolled state. Moreover， the average attenuation rate of torsional vibration under the starting-stopping conditions during vehicle travel is 12.1% and 23.6%， respectively. This proposed method effectively attenuates the torsional vibrations of the driveline during engine starting and stopping conditions， thereby improving the NVH （noise， vibration， and harshness） performance of the hybrid electric vehicle during these operational states.

Keywords： planetary hybrid powertrains; start-stop conditions; torsional vibration; active control; adaptive fuzzy control

混合动力汽车是一种将内燃机技术和电驱动技术相结合的集成创新成果，兼具了传统内燃机汽车长续航、动力特性和电动汽车低排放的优势，成为当前各大汽车厂商的研发热点[1]。混合动力汽车可根据实时功率需求动态调整车辆的驱动模式，但是驱动模式的转换易出现转矩波动，影响整车动力传动的平顺性[2]。且模式切换必然存在频繁的发动机启停[3]，极易诱发混合动力传动系统产生扭转振动问题，引发整车冲击振动，进而影响车辆舒适性[4-5]。

混合动力汽车发动机启停工况扭转振动问题已经成为当前重点研究内容。Tang等[6]针对多电机混合动力汽车模式切换过程中发动机启停引发的扭振问题，采用联合仿真研究了该工况的振动特性，提出发动机不平衡扭矩补偿和传递路径隔振2种控制方法，并通过仿真验证了有效性；Liu等[7]通过仿真与试验指出行星混联式混合动力汽车传动系运动学上的不解耦会导致发动机启停工况下车辆的振动噪声问题，发现曲轴位置对发动机启动工况的阶次振动有明显的影响；Su等[8]指出行星混联式混合动力汽车发动机启动工况下传动系统扭振问题主要是由发动机扭矩脉动引起；熊伟威等[9]提出采用电机调速的方式来降低发动机启动过程负载扭矩波动引起的转速波动，并进行了建模仿真研究，但是未对发动机启动喷油点火过程的扭矩波动问题进行研究；Canova等[10]针对含BSA（belted starter/alternator）电机的轻混车辆发动机启停工况扭振主动控制，提出前馈+反馈的控制方法；秦大同等[11]针对并联式混合动力汽车行进间发动机启动引起的冲击振动问题开展研究，提出通过控制离合器结合状态来控制因发动机点火引起的整车平顺性问题；胡云峰等[12]提出了三步法发动机启停控制器，改善混联式混合动力汽车发动机启动过程的平稳性；赵治国等[13]提出一种发动机停机优化控制策略，以降低发动机再次启动引起的车辆平顺性问题。文献分析可知，当前针对行星混联式混合动力传动系发动机启停工况扭振控制，主要是通过改善发动机的启动控制策略来降低发动机启动过程的扭转振动，而对发动机停机工况扭转振动没有效果；若在发动机启停过程中实时调整电机电磁阻尼力，则可实现发动机启停工况扭振主动控制，无须对传动系进行结构上的改动即可实现传动系扭振主动控制，为提升车辆NVH性能提供一种新思路。

基于上述分析，笔者对行星混联式混合动力汽车启停工况传动系扭振主动控制问题展开研究。首先对行星混联式混合动力汽车涉及发动机启停工况的车辆行驶模式进行了分析；其次建立了传动系动力学仿真模型和发动机启停控制模型；基于振动主动控制理论，设计并提出了自适应模糊扭振主动控制策略；最后利用建立的混合动力汽车传动系仿真模型验证了该控制方法的有效性。

1 启停工况混合动力传动系建模

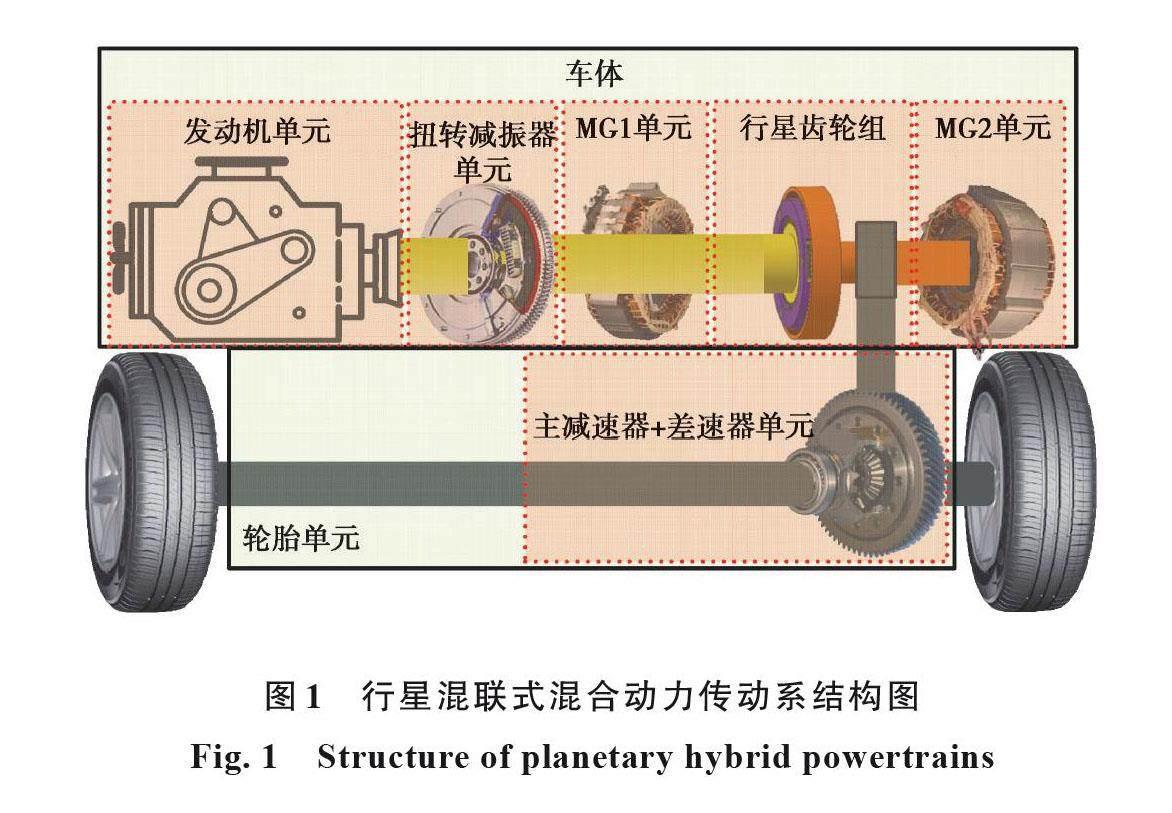
研究对象为某型行星混联式混合动力汽车传动系统，其结构如图1所示。该型混合动力传动系的动力源分别为发动机、电机1和电机2。发动机通过扭转减振器与行星变速箱的行星架相连，电机1与行星变速箱的太阳轮相连，电机2与行星变速箱的齿圈相连，齿圈与主减速器输入端相连，为车辆行驶提供动力。为适应车辆不同运行工况，充分发挥发动机、电机的各自优势，混合动力汽车需要根据运行工况，切换不同工作模式，通过对发动机启停工况的模式类型进行分析，可以将发动机启停工况分为2类：定置停车状态启停工况和车辆行进间启停工況。

基于单元建模的思想，简化得到混合动力汽车传动系单元结构，如图2所示。行星混联式混合动力汽车传动系主要可分为发动机、扭转减振器、电机、行星齿轮及整车等效负载。

1.1 发动机单元模型

1.1.1 发动机单缸扭矩模型

发动机曲柄连杆机构是由活塞、连杆和曲轴等部件组成的复杂系统，其结构简图如图3所示[14-15]。图中：α为曲轴转角；β为连杆摆动角度；r为曲柄半径；L为连杆长度；m_p为活塞组件及连杆部分的等效质量；P_gas为缸内压力。

由图3可得曲轴转角与活塞位移x_p的关系：

x_p=r+rcosα+L-L√（1-λ^2 sin^2 α）。    （1）

式中，λ=r?L。

设曲轴角速度为ω，则

α=ωt。 （2）

发动机气体作用力存在2种状态。

1）发动机工作状态。发动机工作运行状态下，发动机燃油缸内燃烧产生的气体力为

F_（g，j）^+=（P_（gas，j）^+ （α）-P_0）（πD^2）/4。      （3）

式中：F_（g，j）^+为第j个气缸产生的燃烧气体作用力；P_（gas，j）^+ （α）为第j个气缸内燃烧气体产生的缸内压力随α变化的函数；P0为大气压力；D为气缸直径。

2）发动机反拖状态。发动机反拖时气缸内不喷燃油，缸内不存在燃油燃烧做功的过程，但由于进排气门仍然按照正常的气门时序工作，即发动机进、排气过程仍然在进行，此时发动机压缩空气做功，产生的空气作用力阻碍发动机运转，从而产生反拖阻力矩[16]。

F_（g，j）^-=（P_（gas，j）^- （α）-P_0）（πD^2）/4，  （4）

P_（gas，j）^- （α）=〖（V_a/（V（α）））〗^k P_0，   （5）

V（α）=V_c-（πD^2）/4 x_p。   （6）

式中：F_（g，j）^-为第j个气缸产生的空气作用力；P_（gas，j）^- （α）为第j个气缸内压缩空气产生的缸内压力随α变化的函数；Va为气缸总容积；V（α）为气缸容积随α变化的函数；k为绝热系数；Vc为燃烧室容积。

发动机气体作用力在曲轴产生的扭矩计算公式为：

T_（g，j）=K（α）F_（g，j） r，  （7）

式中：K（α）为转换系数；F_（g，j）为气体作用力。

K（α）=sinα+λsin2α/〖2√（1-（λsinα））〗^2 ；   （8）

F_（g，j）={（F_（g，j）^+，发动机运行工况；@F_（g，j）^-，发动机反拖工况。）┤ （9）

发动机惯性力矩主要由活塞往复运动的惯性力引起，根据牛顿第二定律，可得活塞运动方程：

F_（p，j）+sign（sinα）?m_p g=m_p x ¨_p。   （10）

式中，F_（p，j）为第j个气缸产生的往复惯性力。

发动机往复惯性力在曲轴产生的扭矩计算公式为

T_（p，j）=K（α）F_（p，j） r。  （11）

式中，T_（p，j）为第j个气缸产生的惯性力矩。

1.1.2 发动机单缸摩擦模型

发动机摩擦力矩分为多个系统结构的摩擦力矩，分别为：活塞环黏性摩擦力矩Tf1、活塞环混合摩擦力矩Tf2、活塞裙部摩擦力矩Tf3、气门组摩擦力矩Tf4、附件摩擦力矩Tf5和主轴承摩擦力矩Tf6，各部分详细计算见文献[17-18]，综合可得发动机单缸总摩擦力矩：

T_（F，j）=∑_（j'=1）^6?T_fj' 。 （12）

1.1.3 四缸汽油发动机模型

根据四缸发动机相位角关系，由发动机单缸扭矩得到发动机四缸总的输出扭矩：

T_engine=∑_（j=1）^4?〖（T_（p，j）+sign（κ）T_（g，j）-T_（F，j））〗。  （13）

式中，κ表征发动机状态变量，sign（κ）取1时发动机为熄火状态，取1时发动机为工作运行状态。

1.2 扭转减振器模型

文中采用的扭转减振器模型为

T_damper （θ）=kθ+k/2[（θ-θ_0）tanh（β（θ-θ_0））-（θ+θ_0）tanh（β（θ+θ_0））]+M_0 tanh（βθ ˙）。   （14）

式中：k为扭转减振器扭转刚度；θ0为扭转减振器空行程；M0为扭转减振器摩擦阻尼；β为反正切平滑拟合系数，本文中取100。

1.3 电机电磁阻尼模型

混合动力汽车所用电机是永磁同步电机，其扭矩输出数学模型为[19]

T_em=3/2 p（ψ_f i_q+（L_d-L_q）i_d i_q）。      （15）

式中：i为电流；ψ为磁链；下标d、q分别为电机旋转坐标系中的直轴和交轴分量；ψf为永磁体磁链；Tem为电磁转矩；p为电机极对数。

当电机采用id=0控制策略时，其扭矩模型可进一步简化为：

T_em=3/2 pψ_f i_q。    （16）

由式（16）可知，通过调整q轴电流可动态调整电机电磁阻尼力矩的大小。由于电机扭矩特性的限制，其产生的电磁阻尼力还受转速约束，图4为某型電机的阻尼力矩外特性曲线。

由图4可知，在未达到电磁阻尼力矩边界时，通过调节电流大小可调整电机输出可行域内的任意阻尼力矩值；当达到边界条件时，其输出最大阻尼力矩为边界值。因此电机的阻尼力矩特性可表示为：

T_em=min[3/2 pψ_f i_q，f_b （n_em）]?sign（n_em）。    （17）

式中：nem为电机转速；fb（·）为边界条件函数。

1.4 行星齿轮组模型

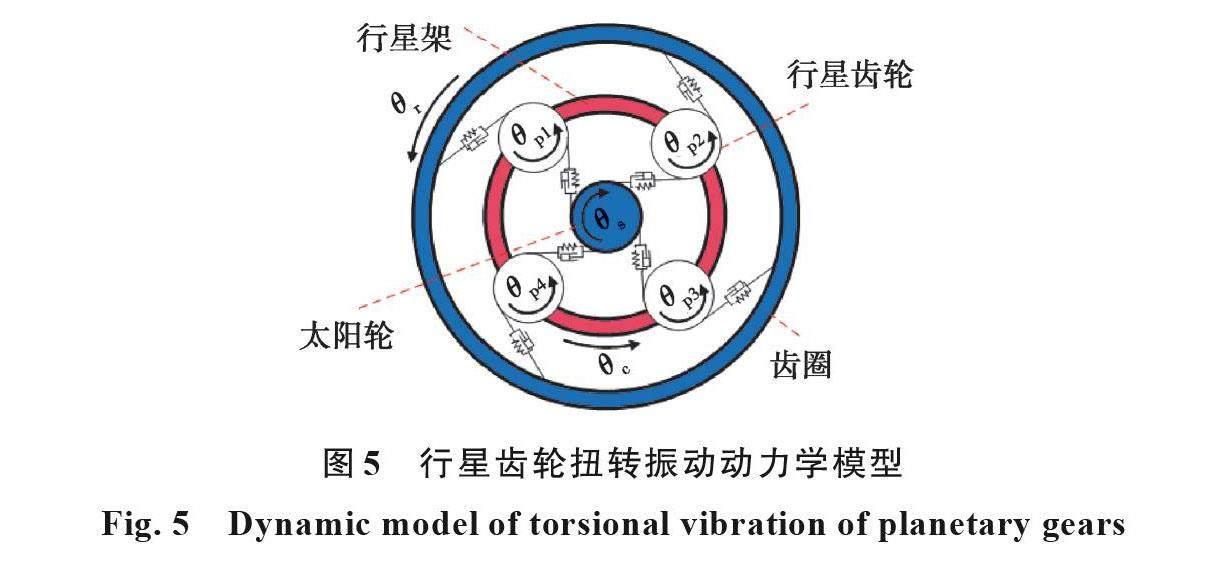
行星混联式混合动力汽车的变速箱为行星齿轮组[20]，本文仅研究各构件在垂直于旋转轴线时的平面扭转运动，认为各构件为刚体，各行星轮均匀分布且性能参数相同，不考虑行星齿轮组的啮合间隙、啮合误差，忽略啮合刚度的时变特性，简化后的扭转振动动力学模型如图5所示。

根据行星齿轮动力学模型，由牛顿力学定律可得其动力学方程如下。

行星架：

（J_c+∑_（n=1）^4?J_（p，n） +Nm_（p，n） 〖r_c〗^2）θ ¨_c+r_c k_cu θ_c-∑_（n=1）^4?〖k_（r，n） δ_（r，n） cosα_r 〗-∑_（n=1）^4?〖k_（s，n） δ_（s，n） cosα_s 〗=0。     （18）

内齿圈：

J_r θ ¨_r+r_r k_ru θ_r+∑_（n=1）^4?〖k_（r，n） δ_（r，n） 〗=0。 （19）

太阳轮：

J_s θ ¨_s+r_s k_su θ_s+∑_（n=1）^4?〖k_（s，n） δ_（s，n） 〗=0。    （20）

行星轮：

J_（p，n） θ ¨_（p，n）-k_（r，n） δ_（r，n）+k_（s，n） δ_（s，n）=0（n=1，2，…，N），     （21）

δ_（s，n）=θ_s+θ_（p，n）-θ_c cosα_s；δ_（r，n）=θ_r-θ_（p，n）-θ_c cosα_r。

式中：N为行星齿轮个数；Jc、Jr、Js和Jp，n分别为行星架、内齿圈、太阳轮和行星轮转动惯量；mp，n为行星轮质量；θc、θr、θs、θp，n分别为行星架、内齿圈、太阳轮、行星轮转动角位移；δs，n和δr，n分别为太阳轮、内齿圈与第n个行星轮产生的相对角位移；αs、αr分别为内啮合与外啮合的啮合角；rc为行星架回转半径；rr、rs分别为内齿圈和太阳轮的基圆半径；ksu为太阳轮轴扭转刚度；kcu、kru为行星架扭转刚度和内齿圈扭转刚度；kr，n和ks，n分别为第n个行星轮和内齿圈与太阳轮的啮合刚度。

2 启停工况扭振主动控制策略

2.1 发动机启停工况控制逻辑

行星混联式混合动力汽车不论是在停车状态下还是车辆行进间，发动机启停过程的控制逻辑基本一致。车辆发出发动机启动信号后，电机1输出扭矩带动发动机转动，当发动机转速达到设定阈值时，发动机ECU控制发动机开始喷油点火，实现发动机的启动；发动机停机过程较为简单，汽车发出停机信号后，发动机停止喷油点火，进而实现发动机停机熄火工况，整个发动机启停工况下，启动电机1扭矩输出和发动机节气门开度的控制量变化如图6所示。

2.2 启停工况扭振主动控制策略设计

根据上一节分析可知，发动机启停过程中，电机1只在启动初始时刻输出扭矩拖动发动机到点火阈值转速，其他时刻驱动电机处于随动状态。通过控制电机1产生电磁阻尼力矩，对转速波动进行抑制与衰减，则可实现混合动力汽车发动机启停工况下传动系扭振主动控制。自适应模糊扭振主动控制策略的控制逻辑如图7所示。

笔者设计的自适应模糊控制包含一个双输入单输出模糊控制器，选取的控制器输入为扭转减振器输出端转速波动值和波动角加速度，电机1产生的期望阻尼力矩为输出量，减振器输出端转速波动期望值取0。定义模糊控制输入输出模糊子集为

input1={NL，NM，NS，ZO，PS，PM，PL}，

input2={NL，NS，ZO，PS，PL}，

output={NL，NM，NS，ZO，PS，PM，PL}。

式中：NL表示负大；NM表示负中；NS表示负小；ZO表示零；PS表示正小；PM表示正中；PL表示正大。

相应的模糊论域分别为

（input1=[-4，4]，@input2=[-3，3]，@output=[-4，4]。）

上述3个变量隶属度函数都采用高斯函数，模糊控制规则曲面如图8所示。

发动机转速对其扭矩波动也存在较大影响，以停机过程发动机阻力矩为例，根据文献[12]试验结果可知，发动机的扭矩波动幅值随着转速的增大而呈现增大趋势，因此，采用固定的比例因子会因转速的快速变化而影响最终控制效果，据此提出一种根据发动机波动转速能够自适应变化的比例因子k3，其表达式为

k_3=λK_3，      （22）

λ=1/（1+e^（-（（n-n_0））/τ） ）。      （23）

式中：K3为比例因子k3的基本值；λ为自适应调整系数；n为发动机波动转速；n0为转速阈值；τ为发动机转速缩放因子。自适应调整系数λ随发动机转速n的变化规律如图9所示。

3 仿真分析

根据前文所建立的发动机启停工况行星混联式混合动力汽车传动系动力学方程和启停工况仿真控制策略，采用MATLAB/Simulink搭建动态仿真模型，对混合动力汽车发动机启停工况传动系扭转振动及其主动控制进行仿真分析。

3.1 定置停车发动机启停

车辆处于停车定置状态，即行星齿轮外齿圈处于静止状态，发动机启停工况下传动系各部件仿真结果如图10所示。

由图10可知，本文所搭建的传动系仿真模型和发动机启停工况仿真策略可有效反映发动机启停工况下混合动力传动系的动态特性。仿真时间0.0～0.2 s时，电机1输出启动力矩拖动发动机转动，此时转速波动是由发动机反拖过程的内部摩擦和活塞压缩空气产生的阻力矩引起；在0.2 s时，由发动机启停控制逻辑可知，发动机开始喷油点火，电机1停止输出，此后发动机开始输出扭矩并带动行星架转动，转速波动的产生也是由发动机输出扭矩波动所引起；在4.0 s时，发动机熄火，传动系转速最终都为0。整个发动机启停过程齿圈转速始终为0，说明变速箱没有转速输出，汽车处于停车静止状态。

由图10可知，发动机启停过程中，传动系转速出现了非常明显的大幅度波动，可能引发车辆NVH问题。为有效抑制这一过程的转速波动，笔者提出了基于电机电磁阻尼力矩自适应模糊控制的传动系扭振主动控制方法，其仿真结果如图11～12所示。

图11为自适应模糊控制发动机启停工况仿真结果。图12为主动控制前后发动机输出转速波动与变速器输入转速差值，用来表征启停工况转速波动大小。由图12可知，发动机启动和停机工况下，自适应模糊控制策略能够有效抑制混合动力传动系的转速波动。为量化本文所提方法的减振性能，分别取相对角速度的峰值Δθpp[21]和最大绝对值|Δθ|的衰减率进行评价，其结果如表1所示。

由表1可知，混联式混合动力汽车在定置停车发动机启停工况下，扭振主动控制相比无控制，发动机启动和停机工况转速波动平均衰减率分别为23.8%和30.1%，说明本文方法有效。

3.2 车辆行进间发动机启停

首先车辆以纯电动工况行驶，4.0 s后发动机开始点火，执行点火控制程序，整个过程车辆处于行驶状态，行进间发动机启停工况下传动系各部件仿真结果如图13所示。

由图13可知，在0.0～4.0 s，发动机、扭转减振器和行星架转速为0，发动机为停机状态；电机2输出扭矩驱动齿圈转动，车速从0开始起步加速，同时根据行星齿轮变速箱啮合关系，行星轮和太阳轮也发生转动；第4.0 s时，发动机启动控制策略输出启动指令，电机1输出扭矩驱动太阳轮进而带动行星架-扭转减振器-发动机转动，当发动机转速达到点火转速（第4.2 s时），发动机开始点火同时电机1扭矩变为0，从而完成车辆行进间的发动机启动工况。可发现发动机点火启动瞬间对车速有一定影响。第6.0 s时，发动机熄火，发动机转速以及離合器、行星架转速变为0，汽车车速降低。进一步分析扭振主动控制传动系仿真结果，如图14和15所示。

圖14为自适应模糊控制行进间发动机启停工况仿真结果。图15为控制前后行进间发动机输出转速波动与变速器输入转速波动差值。由图可知，自适应模糊控制行进间发动机启停工况下转速波动有明显的降低，有效抑制了行进间发动机启停工况转速波动，衰减率评价指标如表2所示。

由表2可知，自适应模糊扭振主动控制下，车辆行进间发动机启动工况和停机工况的转速波动平均衰减率分别为12.1%和23.6%，说明本文方法在行进间发动机启停工况也是有效的。

4 结束语

1）建立了考虑发动机扭矩波动和启停控制逻辑的行星混动汽车发动机启停工况动力学仿真模型，模型包括发动机、扭转减振器、电机以及行星齿轮变速箱，构建发动机启停控制逻辑和启停工况扭振主动控制策略，进行了车辆定置停车发动机启停和行进间发动机启停仿真研究。

2）提出了发动机启停传动系扭振自适应模糊主动控制策略，对比分析了扭振主动控制和无控制下发动机启停工况传动系扭转振动。结果表明笔者提出的方法相比无控制，停车状态发动机启动工况和停机工况的扭振平均衰减率分别为23.8%和30.1%；车辆行进间发动机启动和停机工况的扭振平均衰减率分别为12.1%和23.6%。本文方法可有效减轻发动机启停工况传动系扭振，提升车辆发动机启停工况的NVH性能。

参考文献

［1］  Shigeta N， Hosseini S E. Sustainable development of the automobile industry in the United States， Europe， and Japan with special focus on the vehicles power sources[J]. Energies， 2020， 14（1）： 78.

［2］  林歆悠， 郑清香， 吴超宇. 基于GA-ECMS电机转矩优化的混合动力系统协调控制[J]. 机械工程学报， 2020， 56（2）： 145-153.

Lin X Y， Zheng Q X， Wu C Y. Coordinated control of hybrid electric powertrain based on GA-ECMS motor torque optimization[J]. Journal of Mechanical Engineering， 2020， 56（2）： 145-153.（in Chinese）

［3］  莫崇相， 修彩靖， 梁万武. P2混合动力发动机启动控制设计[J]. 中国机械工程， 2021， 32（1）： 117-125.

Mo C X， Xiu C J， Liang W W. Design of P2 hybrid engine start control[J]. China Mechanical Engineering， 2021， 32（1）： 117-125.（in Chinese）

［4］  张欣， 崔宇轩， 薛奇成. PHEV行进间启动发动机的转矩协调控制策略[J]. 华南理工大学学报（自然科学版）， 2021， 49（8）： 129-139.

Zhang X， Cui Y X， Xue Q C. Torque coordinated control strategy of PHEV engine starting in motion process[J]. Journal of South China University of Technology （Natural Science Edition）， 2021， 49（8）： 129-139.（in Chinese）

［5］  潘云伟， 颜伏伍， 刘宗成， 等. 混动汽车启动抖动问题分析及优化[J]. 重庆理工大学学报（自然科学）， 2020， 34（2）： 64-68.

Pan Y W， Yan F W， Liu Z C， et al. Analysis and optimization of starting jitter of hybrid vehicles[J]. Journal of Chongqing University of Technology （Natural Science）， 2020， 34（2）： 64-68.（in Chinese）

［6］  Tang X L， Zhang D J， Liu T， et al. Research on the energy control of a dual-motor hybrid vehicle during engine start-stop process[J]. Energy， 2019， 166： 1181-1193.

［7］  Liu D H， Yu H S， Zhang J W. Multibody dynamics analysis for the coupled vibrations of a power split hybrid electric vehicle during the engine start transition[J]. Proceedings of the Institution of Mechanical Engineers， Part K： Journal of Multi-Body Dynamics， 2016， 230（4）： 527-540.

［8］  Su Y Z， Hu M H， Huang J， et al. Experimental and characteristic analysis during the engine start-up process for a compound power-split hybrid electric vehicle[J]. Applied Sciences， 2021， 11（4）： 1846.

［9］  熊伟威， 张勇， 殷承良. 混合动力汽车的电机启动发动机过程仿真研究[J]. 中国机械工程， 2008， 19（20）： 2504-2509.

Xiong W W， Zhang Y， Yin C L. Process simulation of engine started by motor in a hybrid electric vehicle[J]. China Mechanical Engineering， 2008， 19（20）： 2504-2509.（in Chinese）

［10］  Canova M， Guezennec Y， Yurkovich S. On the control of engine start/stop dynamics in a hybrid electric vehicle[J]. Journal of Dynamic Systems， Measurement， and Control， 2009， 131（6）： 1.

［11］  秦大同， 尚阳， 杨官龙. 插电式混合动力汽车纯电动行进间启动发动机的平顺性控制[J]. 重庆大学学报， 2015， 38（4）： 1-9.

Qin D T， Shang Y， Yang G L. The ride comfort control of PHEV during engine starting in-motion process[J]. Journal of Chongqing University， 2015， 38（4）： 1-9.（in Chinese）

［12］  胡云峰， 顾万里， 梁瑜， 等. 混合动力汽车启停非线性控制器设计[J]. 吉林大学学报（工学版）， 2017， 47（4）： 1207-1216.

Hu Y F， Gu W L， Liang Y， et al. Start-stop control of hybrid vehicle based on nonlinear method[J]. Journal of Jilin University （Engineering and Technology Edition）， 2017， 47（4）： 1207-1216.（in Chinese）

［13］  赵治国， 唐旭辉， 付靖， 等. 功率分流混合动力系统发动机停机优化控制[J]. 汽车工程， 2020， 42（8）： 993-999， 1007.

Zhao Z G， Tang X H， Fu J， et al. Optimal control of engine shutdown for power-split hybrid system[J]. Automotive Engineering， 2020， 42（8）： 993-999， 1007.（in Chinese）

［14］  Ipci D， Karabulut H. Thermodynamic and dynamic modeling of a single cylinder four stroke diesel engine[J]. Applied Mathematical Modelling， 2016， 40（5/6）： 3925-3937.

［15］  Chen L， Shi W K， Chen Z Y. Research on damping performance of dual mass flywheel based on vehicle transmission system modeling and multi-condition simulation[J]. IEEE Access， 2020， 8： 28064-28077.

［16］  边浩然， 徐正飞， 曾繁琦， 等. 基于ISG的军用混合动力车辆发动机启动性能仿真[J]. 军事交通学院学报， 2017， 19（9）： 30-34， 39.

Bian H R， Xu Z F， Zeng F Q， et al. Start-up performance simulation of military hybrid vehicle engine based on ISG[J]. Journal of Military Transportation University， 2017， 19（9）： 30-34， 39.（in Chinese）

［17］  Rezeka S F， Henein N A. A new approach to evaluate instantaneous friction and its components in internal combustion engines[J]. SAE Transactions，1984， 93： 932-944.

［18］  Zweiri Y H， Whidborne J F， Seneviratne L D. Dynamic simulation of a single-cylinder diesel engine including dynamometer modelling and friction[J]. Proceedings of the Institution of Mechanical Engineers， Part D： Journal of Automobile Engineering， 1999， 213（4）： 391-402.

［19］  唐任远. 现代永磁电机理论与设计[M]. 北京： 机械工业出版社， 1997： 85-89.

Tang R Y. Modern permanent magnet synchronous machines[M]. Beijing： China Machine Press， 1997： 85-89. （in Chinese）

［20］  張立军，朱文栋. 基于纯扭转模型的行星齿轮系统固有振动特性仿真分析[C]//2013中国汽车工程学会年会论文集.北京：北京理工大学出版社，2013：890-893.

Zhang L J， Zhu W D. Numerical analysis of natural vibration characteristics of planetary gear system based on pure torsional model[C]// 2013 SAE-China Congress Selected Papers. Beijing： Beijing Institute of Technology Press， 2013：890-893. （in Chinese）

［21］  Li L H， Singh R. Start-up transient vibration analysis of a vehicle powertrain system equipped with a nonlinear clutch damper[J]. SAE International Journal of Passenger Cars - Mechanical Systems， 2015， 8（2）： 726-732.

（编辑  吕建斌）