基于超像素分割的图注意力网络的高光谱图像分类

高路尧　胡长虹　肖树林

摘要： 针对卷积神经网络（CNN）仅能应用于欧氏数据， 無法有效获取像素间的全局关系特征以及长距离上下文信息的问题， 构建一个基于超像素分割的图注意力网络SSGAT. 该网络将超像素分割后的超像素块视为图结构中的图节点， 有效减少了图结构的复杂度， 并降低了分类图的噪声. 在3个数据集上对SSGAT及对比算法的分类精度进行测试， 分别获得了94.11%，95.22%，96.37%的总体分类精度. 结果表明该方法性能优异， 在处理大尺度区域的分类问题时优势明显.

关键词： 高光谱图像； 图注意力网络； 残差机制； 超像素分割

中图分类号： TP391文献标志码： A文章编号： 1671-5489（2024）02-0357-12

Hyperspectral Image Classification Based on SuperpixelSegmentation with Graph Attention Networks

GAO Luyao1，2， HU Changhong1， XIAO Shulin1，2

（1. Changchun Institute of Optics， Fine Mechanics and Physics， Chinese Academy of Sciences，Changchun 130033， China； 2. University of Chinese Academy of Sciences， Beijing 100049， China）

Abstract： Aiming at the problem that convolutional neural network （CNN） could only be applied to Euclidean data and could not effectively obtain global relationship features between pixels and long-distance contextual information， we constructed a superpixel segmentation-based graph attention network （SSGAT）. The network treated the segmented superpixel blocks as graph nodes in the graph structure， effectively reducing the complexity of the graph structure and reducing the noise of the classification graph.  The classification accuracy of SSGAT and the comparison algorithm were tested on three datasets， and overall classification accuracy of 94.11%， 95.22%， and 96.37% were obtained， respectively. The results show that the method has excellent performance and significant advantages in dealing with classification problems in large-scale regions.

Keywords： hyperspectral image; graph attention network; residual mechanism; superpixel segmentation

高光谱成像系统可同时获取地物丰富的光谱信息和二维空间信息进而形成高光谱图像（hyperspectral images， HSI）［1］. HSI的光谱维度由数十至数百个连续波段组成， 细微的光谱特征极大提升了地物分辨能力， 因此已广泛应用于灾害监测、 植被分类、 精细农业以及医学诊断等领域［2-5］.

HSI分类的目标是对HSI中的各像素所代表的地物对象进行判别［6］. 早期主要依靠一些机器学习算法进行高光谱图像分类任务， 传统的机器学习算法主要分为特征工程与分类器分类两个过程. 特征工程的目的是根据专业知识对数据进行处理， 从而使处理后的特征在后续分类算法中得到更好地应用， 例如主成分分析（PCA）［7］、 独立成分分析（ICA）［8］等降维方法. 典型的分类器包括支持向量机（SVM）［9］、 随机森林（RF）［10］和k-近邻（KNN）［11］等方法. 但上述方法忽略了HSI中的空间信息， 且特征提取过程需人为参与， 因此限制了分类准确度的提升.

深度学习通过聚合低级特征自动对图像的高阶特征进行提取， 避免了繁琐的特征工程， 且能取得比机器学习方法更好的分类结果［5］， 因此， 已经替代了传统的机器学习分类方法［12］. 其中， 卷积神经网络（CNN）由于具有局部连接、 权值共享的特点已成为高光谱分类领域的主流方法［13］. 首先被用于HSI分类任务的深度学习方法是一维卷积（1DCNN）和二维卷积神经网络（2DCNN）［14-15］， 一维卷积将每个波段的像素点视为一个序列， 而二维卷积将每个波段的像素视为一个矩阵， 这类方法的分类结果均优于机器学习方法， 但仍存在对图像的空间及光谱信息利用不足的问题. 因此， Chen等［4］提出了三维卷积神经网络（3DCNN）模型以同时提取空谱联合特征， 相比二维卷积， 3DCNN可以同时在3个方向上进行卷积操作， 进而提取更多的特征信息， 该方法实现了对空谱信息的同步提取， 但该模型的计算负担较大. 为解决上述问题并提取更丰富的特征， 研究者提出了一种混合光谱CNN（HybridSN）［5］， 使图像先经过三维卷积处理再经过二维卷积处理， 在获取丰富特征的同时计算负担比3DCNN方法小［16］.

为分析并利用数据之间的关联性， 突出重要的特征并忽略不相关的噪声信息， 人们提出了注意力机制. Mei等［17］使用基于空间注意力的卷积神经网络进行HSI分类， 通过对像素周围的区域进行空间注意力卷积进而提高了分类精度. Yang等［18］将二维卷积与三维卷积相结合， 增添了一个三维注意力模块以获取更丰富的特征. 为解决网络层数增加导致的过拟合问题， Zhong等［19］将残差结构引入3DCNN模型， 构建了光谱残差模块和空间残差模块， 取得了较满意的分类结果； Wang等［20］提出了一种基于残差和注意力机制的深度卷积神经网络， 通过引入注意力机制和残差连接提高了分类精度和鲁棒性.

虽然目前基于CNN的分类方法应用广泛， 但CNN中的卷积操作是通过平移卷积核实现的， 其工作方式导致其只能应用于规则数据的处理， 卷积核的大小又限制了其获取长距离上下文特征的能力， 忽视了对高光谱图像分类任务有帮助的关系特征， 很难对不规则数据进行处理. 为解决上述问题， 研究者们借鉴卷积网络的思想设计了图卷积网络， 并将其应用在HSI分类任务中［21］.

图卷积网络通过捕获并聚合图结构中各节点及其相邻节点之间的关系获取上下文信息， 图结构的不规则性导致在图结构上直接进行卷积非常困难. 基于空域中卷积的Fourier变换等于频域中的Fourier变换的乘积［22］， Kipf等［23］首先提出了频域图卷积网络模型， 先将空域输入信号和空域卷积核转换到频域， 在谱域中相乘后再通过Fourier逆变换转换回空域. Velikovic等［24］提出了图注意力网络（graph attention network， GAT）， GAT利用注意力机制对邻域节点进行聚合操作， 可对不同节点之间的关系进行不同程度的加权， 从而提高了模型对关键节点的关注度， 并使模型能更好地捕捉节点之间的全局关系. Wang等［25］则在高光谱图像的光谱维度上构建多尺度金字塔， 在每个尺度空间应用GAT方法提取特征， 最后实现分类任务. Sha等［26］提出了一种新的基于图注意力网络的分类框架以充分利用空谱信息.

针对基于CNN的分类方法无法有效获取像素间的关系特征、 难以对不规则数据进行处理等问题， 本文构建一个基于超像素分割的图注意力网络SSGAT（superpixel segmentation-based graph attention networks）， 并通过与其他主流方法进行对比实验和消融实验， 对提出的SSGAT方法进行评估， 实验结果证明了本文算法性能优异.

1 实验方法

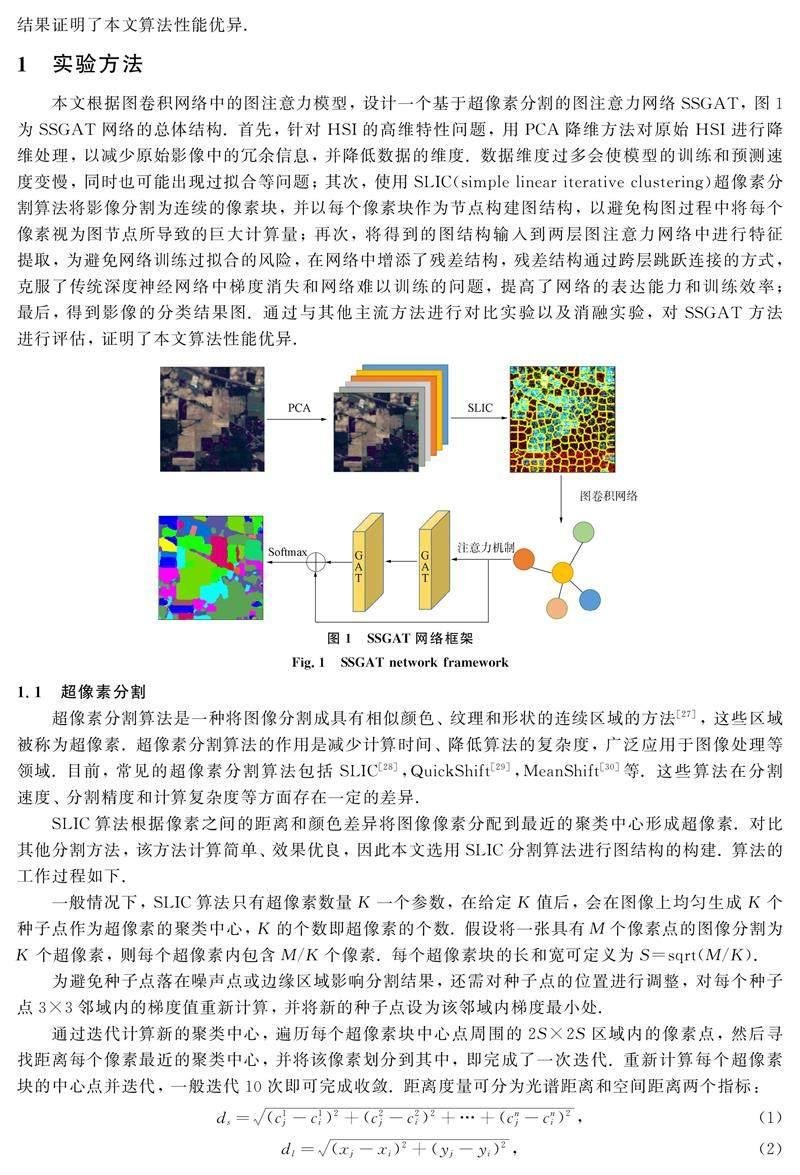
本文根据图卷积网络中的图注意力模型， 设计一个基于超像素分割的图注意力网络SSGAT， 图1为SSGAT网络的总体结构. 首先， 针对HSI的高维特性问题， 用PCA降维方法对原始HSI进行降维处理， 以减少原始影像中的冗余信息， 并降低数据的维度. 数据维度过多会使模型的训练和预测速度变慢， 同时也可能出现过拟合等问题； 其次， 使用SLIC（simple linear iterative clustering）超像素分割算法将影像分割为连续的像素块， 并以每个像素块作为节点构建图结构， 以避免构图过程中将每个像素视为图节点所导致的巨大计算量; 再次， 将得到的图结构输入到两层图注意力网络中进行特征提取， 为避免网络训练过拟合的风险， 在网络中增添了残差结构， 残差结构通过跨层跳跃连接的方式， 克服了传统深度神经网络中梯度消失和网络难以训练的问题， 提高了网络的表达能力和训练效率； 最后， 得到影像的分类结果图. 通过与其他主流方法进行对比实验以及消融实验， 对SSGAT方法进行评估， 证明了本文算法性能优异.

1.1 超像素分割

超像素分割算法是一种将图像分割成具有相似颜色、 纹理和形状的连续区域的方法［27］， 这些区域被称为超像素. 超像素分割算法的作用是减少计算时间、 降低算法的复杂度， 广泛应用于图像处理等领域. 目前， 常见的超像素分割算法包括SLIC［28］，QuickShift［29］，MeanShift［30］等. 这些算法在分割速度、 分割精度和计算复杂度等方面存在一定的差异.

SLIC算法根据像素之间的距离和颜色差异将图像像素分配到最近的聚类中心形成超像素. 对比其他分割方法， 该方法计算简单、 效果优良， 因此本文选用SLIC分割算法进行图结构的构建. 算法的工作过程如下.

一般情况下， SLIC算法只有超像素数量K一个参数， 在给定K值后， 会在图像上均匀生成K个种子点作为超像素的聚类中心， K的个数即超像素的个数. 假设将一张具有M个像素点的图像分割为K个超像素， 则每个超像素内包含M/K个像素. 每个超像素块的长和宽可定义为S=sqrt（M/K）.

为避免种子点落在噪声点或边缘区域影响分割结果， 还需对种子点的位置进行调整， 对每个种子点3×3邻域内的梯度值重新计算， 并将新的种子点设为该邻域内梯度最小处.

通过迭代计算新的聚类中心， 遍历每个超像素块中心点周围的2S×2S区域内的像素点， 然后寻找距离每个像素最近的聚类中心， 并將该像素划分到其中， 即完成了一次迭代. 重新计算每个超像素块的中心点并迭代， 一般迭代10次即可完成收敛. 距离度量可分为光谱距离和空间距离两个指标：ds=（c1j-c1i）2+（c2j-c2i）2+…+（cnj-cni）2，（1）

dl=（xj-xi）2+（yj-yi）2，（2）其中高光谱数据可以用{c1i，c2i，…，cni，xi，yi}表示， ds表示像素i和像素j的光谱距离， {c1i，c2i，…，cni}表示像素i的n个波段内的不同特征， dl表示像素i和像素j的空间距离， （xi，yi）表示像素i的空间坐标. 对两种距离做归一化后可得：D′=ds/Ns2+dl/Nl2=ds/m2+dl/S2，（3）其中： 最大颜色距离Ns随图像的不同而不同， 通过一个参数m表示， 一般取一个固定常数10； Nl是类内最大空间距离， 定义为Nl=S; S为超像素的边长.

SLIC算法因为计算简单、 效果良好的特点被广泛应用在各领域. 本文中超像素的划分数量根据数据集的像素点总数的不同而不同， 因此规定超像素的划分个数为K=（H×W）/β， 其中H和W分别为数据集的长和宽， β为一个控制超像素数量的分割系数.

1.2 GAT网络的构建

2 实验结果与分析

2.1 数据集及评价指标

为测试SSGAT网络的性能， 采用Indian Pines（IP），Pavia University（PU）和Salinas（SA）3个应用广泛的高光谱数据集对网络进行测试与分析. 使用总体分类精度（overall accuracy， OA）、 平均分类精度（average accuracy， AA）和Kappa系数3个指标评估本文算法.

数据集IP是美国农业部应用红外成像光谱仪对一片印度松树进行成像获取的， 图像在去除20个干扰波段后剩余200个波段， 尺寸为145×145， 包含16种土地覆盖类型， 共10 366个样本， 包括玉米、 豆类、 杂草、 棉花等农作物， 以及道路、 建筑物、 阴影等非农作物类别， 每个像素点可被归为16个类别之一. 其假彩色图像及标记样本如图3所示.

数据集PU是使用光谱成像仪对一所大学成像获取的， 在剔除12个干扰波段后剩余103个有效波段， 图像尺寸为610×340， 包含9种土地覆盖类型， 共42 776个样本， 该数据集包括沥青、 草地、 土地、 建筑物、 树木等. 其假彩色图像及标记样本如图4所示.

数据集SA是对美国的一个山谷成像获取的， 在去除20个干扰波段后剩余204个波段， 图像尺寸为512 ×217， 包含16种土地覆盖类型， 共54 215个样本. 其假彩色图像及标记样本如图5所示.

表1～表3分别列出了测试过程中上述3个数据集的样本划分数目. 由于不同数据集的样本总量并不相同， 为准确测试各算法对不同类别样本的分类性能， 因此， 本文对各数据集训练样本的划分比例也不同. 由于数据集IP包含的样本总量较少且各类别之间的数量相差悬殊， 所以在该数据集中随机选取每类样本的15%作为训练样本， 其余样本用于验证及测试. 数据集PU及数据集SA包含的样本总量较多且分布相对均匀， 因此这两个数据集的训练样本数设为每类样本的5%.

2.2 实验参数设置

本文实验基于Python3.8.12语言和Pytorch1.1.0学习框架实现. 用于训练的硬件为i7-10750H CPU和NVIDIA GeForce RTX 2060s GPU. 实验中使用学习率为0.000 1的Adam优化器优化本文模型， 迭代步数设为800. 实验重复进行5次取平均值以减少误差. SSGAT中每个数据集的超像素个数划分为数据集样本总数的1/150. 将第一层图注意力的输出维度设为64， 第二层的输出维度为每个数据集的样本类别数.

2.3 分类结果及分析

为验证本文模型的性能， 选择几种有表示性的HSI分类方法与本文模型进行比较分析， 其中包括机器学习中的SVM［9］、 卷积神经网络中的2DCNN［15］、 3DCNN［16］、 GCN方法［25］和GAT［26］方法. 上述方法均采用原文献中使用的参数， 实验结果重复5次取平均值.

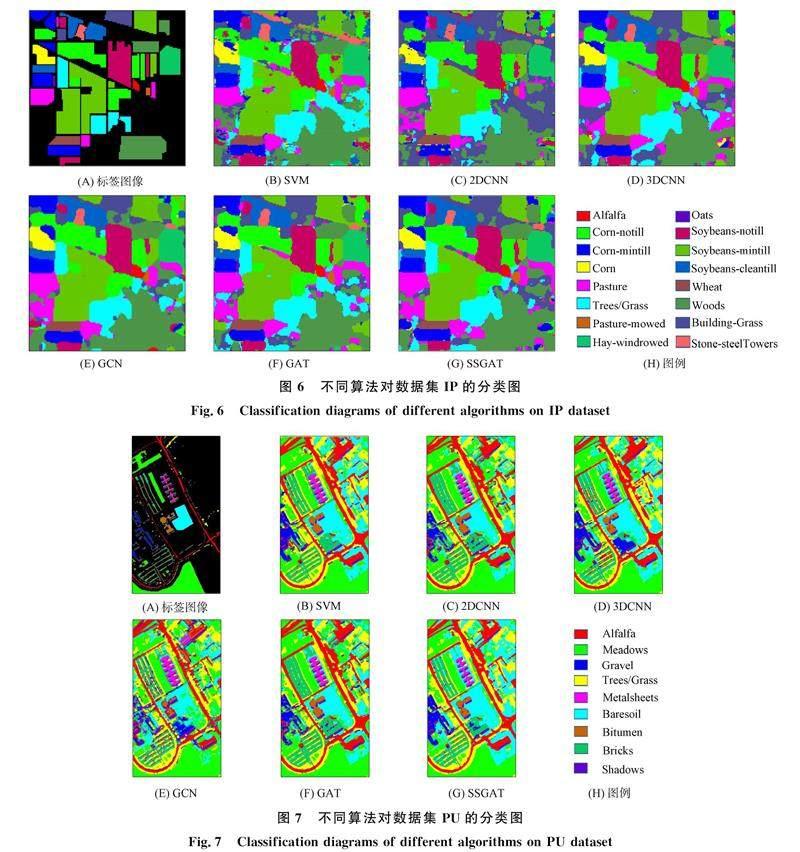
表4～表6分别列出了不同方法在上述3个数据集上的分类准确率、 各方法的训练及测试时间. 实验结果表明， SSGAT在所有数据集中均取得了最优的分类效果， 在3个数据集中总体分类精度OA分别达到了94.11%，95.22%，96.37%. 图6～图8分别为各方法在不同数据集上得到的地物分类图.

由表4可见： 在数据集IP中， 由于SVM方法只关注了HSI的光谱信息， 且特征提取能力弱， 因此分类精度只有75.33%； 2DCNN方法与SVM方法相比无需手动设计特征提取方法， 可自动捕捉图像的深层特征； 3DCNN方法能利用三维卷积核同时获取HSI的空谱特征， 因此3DCNN获得了比2DCNN更高的分类精度， 但其训练时间与测试时间均高于2DCNN； 上述方法忽略了图像的节点特征， 且没有对重要信息进行特别关注； GCN与原始GAT方法得到的OA分别为82.22%和83.99%， 分类精度较差， 但SSGAT获得了94.11%的总体分类精度， 证明了超像素分割及残差结构的增加对网络性能的提升有帮助； SSGAT在第二类及第十二类地物上的分类结果分别达到97.99%和96.38%， 这两类地物的尺度均较大， 证明该网络更适用于对尺度较大的地物进行分类. 该网络的训练时间虽不是最优， 但训练时间相比GAT方法有所下降， 这得益于超像素分割技术的应用. 由图6可见， SSGAT的地物分类图的误分类现象最少， 且相比其他算法噪声最少.

由表5可见， 对比数据集IP上的分类结果， 各方法在数据集PU中的分类精度都有不同程度的提升， 这是因为该数据集包含的训练样本数更多， 使得各模型能更准确地对HSI进行分类. 其中SSGAT在3种精度评价指标下均取得了最好成绩， OA为95.22%， AA为94.41%， Kappa系数为93.33%. 其OA相比于GAT方法， 精度提升了9.74%， 相比于GCN方法精度提升了10.75%. 由图7可见， SSGAT的地物分类图显示效果最好， 误分类最少， 与两种卷积神经网络方法相比更平滑.

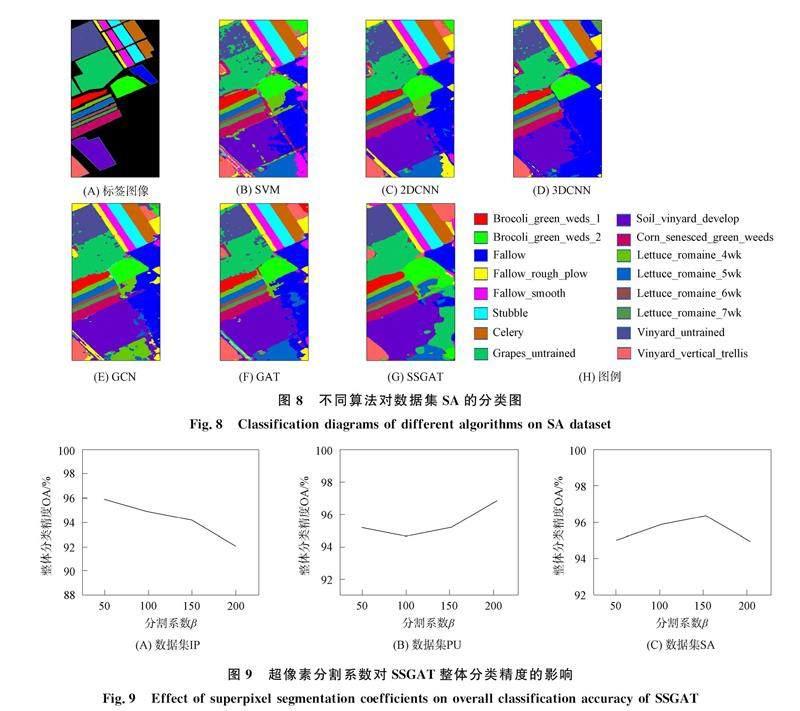
由表6可見， SSGAT在3种精度评价指标下仍取得了最好结果， 整体分类精度为96.37%. 由图8可见， SSGAT算法的误分类最少. 上述实验结果表明， SSGAT的分类能力优异， 且在大尺度区域能获得更好的分类结果.

2.4 超像素数量的影响

在构建图结构前进行超像素分割处理可有效减少计算量并降低分类图中的噪声， 因此本文采用超像素分割技术， 通过分割系数控制超像素的数量和大小， 分割系数越大， 超像素的数量越少， 获得的分割图尺寸越大， 保留更大的物体和抑制更多的噪声. 反之， 分割系数越小， 超像素数量越多， 获得的分割图尺寸越小， 保留更小的物体并包含更多的噪声. 为分析超像素块数量对分类结果的影响， 将分割系数分别设为50，100，150，200， 在每个数据集上测试SSGAT的分类精度， 绘制不同分割系数下的整体分类精度折线图， 结果如图9所示.

由图9可见， SSGAT在数据集IP上的精度随分割系数的增加而降低， 表明数据集IP中存在更多的小物体， 因此更小的系数可保存更多的细节. 在数据集PU上的分类精度随分割系数的增加呈上升趋势， 这是由于与数据集IP中的样本类别相比， 该数据集中类别尺度更大， 分割系数的增加对整体精度的影响很小， 但这种上升关系不会一直保持. 在地物类别尺度更大的数据集SA上， 分类精度随着分割系数的增加先升高后降低， 当分割系数为150时达到峰值. 这是因为分割系数的进一步增大， 使得这些大尺度地物与周围其他类别的像素进行了聚类， 影响了其自身的分类精度. 为防止分类图过于平滑， 本文将分割系数设置为150.

2.5 消融实验

为进一步对SSGAT网络的性能进行分析， 对SSGAT网络进行消融实验， 以验证该网络的合理性. 首先， 为测试残差结构对网络性能的影响， 在数据集划分及实验条件不变的情况下， 在3个数据集上对不设置残差结构的网络结构进行测试， 记为实验一； 其次， 为考察注意力网络层数对网络性能的影响， 将SSGAT中的层数设置为3层进行实验， 记为实验二. 实验结果列于表7.

通过实验一与SSGAT的對比可见， 增添了残差结构的SSGAT在3个数据集上的分类精度均有不同程度的上升， 所以SSGAT中的残差结构对整体网络性能的提升有帮助. 通过实验二与SSGAT的对比可见， 当网络层数变为3层时， 其分类性能并没有预期中的增加. 这是因为层数的进一步增加使网络的参数及计算资源的需求增多， 因此本文将网络层数设置为2.

综上所述， 针对目前的分类方法无法有效获取像素间关系特征的问题， 本文构建了一个基于超像素分割的图注意力网络， 利用图结构对不规则的HSI进行处理， 以获取其上下文信息和依赖关系. 在3个代表性的高光谱图像数据集上对SSGAT及对比算法的分类精度进行测试， 对SSGAT进行对比实验及消融实验， 在3个数据集上分别获得了94.11%，95.22%，96.37%的总体分类精度， 与其他算法相比性能优异， 对大尺度区域的分类问题具有明显优势. 但该方法也存在不足， 超像素分割将HSI中的像素进行了聚合并以相同的特征进行表示， 将每个超像素视为图节点后信息， 只能在每个超像素之间传播， 对超像素内的局部空谱信息提取不足.

参考文献

［1］BIOUCAS-DIAS J M， PLAZA A， CAMPS-VALLS G， et al. Hyperspectral Remote Sensing Data Analysis and Future Challenges ［J］. IEEE Geoscience and Remote Sensing Magazine， 2013， 1（2）： 6-36.

［2］FAUVEL M， TARABALKA Y， BENEDIKTSSON J A， et al. Advances in Spectral-Spatial Classification of Hyperspectral Images ［J］. Proceedings of the IEEE， 2013， 101（3）： 652-675.

［3］MA Z T， JIANG Z G， ZHANG H P. Hyperspectral Image Classification Using Feature Fusion Hypergraph Convolution Neural Network ［J］. IEEE Transactions on Geoscience and Remote Sensing， 2021， 60： 5517314-1-5517314-14.

［4］CHEN Y S， JIANG H L， LI C Y， et al. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks ［J］. IEEE Transactions on Geoscience and Remote Sensing， 2016， 54（10）： 6232-6251.

［5］L W J， WANG X F. Overview of Hyperspectral Image Classification ［J］. Journal of Sensors， 2020（2）： 1-13.

［6］AUDEBERT N， LE S B， LEFEVRE S. Deep Learning for Classification of Hyperspectral Data： A Comparative Review ［J］. IEEE Geoscience and Remote Sensing Magazine， 2019， 7（2）： 159-173.

［7］PRASAD S， BRUCE L M. Limitations of Principal Components Analysis for Hyperspectral Target Recognition ［J］. IEEE Geoscience and Remote Sensing Letters，  2008， 5（4）： 625-629.

［8］VILLA A， BENEDIKTSSON J A， CHANUSSOT J， et al. Hyperspectral Image Classification with Independent Component Discriminant Analysis ［J］. IEEE Transactions on Geoscience and Remote Sensing， 2011， 49（12）： 4865-4876.

［9］MELGANI F， BRUZZONE L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines ［J］. IEEE Transactions on Geoscience and Remote Sensing， 2004， 42（8）： 1778-1790.

［10］GISLASON P O， BENEDIKTSSON J A， SVEINSSON J R. Random Forests for Land Cover Classification ［J］. Pattern Recognition Letters， 2006， 27（4）： 294-300.

［11］HUGHES G. On the Mean Accuracy of Statistical Pattern Recognizers ［J］. IEEE Transactions on Information Theory， 1968， 14（1）： 55-63.

［12］KRIZHEVSKY A， SUTSKEVER I， HINTON G E. Imagenet Classification with Deep Convolutional Neural Networks ［J］. Communications of the ACM， 2017， 60（6）： 84-90.

［13］CHEN Y S， LIN Z H， ZHAO X， et al. Deep Learning-Based Classification of Hyperspectral Data ［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2014， 7（6）： 2094-2107.

［14］HU W， HUANG Y Y， WEI L， et al. Deep Convolutional Neural Networks for Hyperspectral Image Classification ［J］. Journal of Sensors， Hindawi Limited， 2015， 2015： 1-12.

［15］MAKANTASIS K， KARANTZALOS K， DOULAMIS A， et al. Deep Supervised Learning for Hyperspectral Data Classification through Convolutional Neural Networks ［C］//2015 IEEE International Geoscience and Remote Sensing Symposium （IGARSS）. Pisataway， NJ： IEEE， 2015： 4959-4962.

［16］盧佳， 保文星. 基于独立空谱残差融合的联合稀疏表示高光谱图像分类 [J]. 计算机工程， 2019， 45（1）： 246-252. （LU J， BAO W X. Hyperspectral Image Classification Based on Joint Sparse Representation of Independent Spatial-Spectral Residual Fusion [J]. Computer Engineering， 2019， 45（1）： 246-252.）

［17］MEI X G， PAN E T， MA Y， et al. Spectral-Spatial Attention Networks for Hyperspectral Image Classification ［J］. Remote Sensing， 2019， 11（8）： 963-1-963-18.

［18］YANG X E， ZHANG X F， YE Y M， et al. Synergistic 2D/3D Convolutional Neural Network for Hyperspectral Image Classification ［J］. Remote Sensing， MDPI， 2020， 12（12）： 2033-1-2033-19.

［19］ZHONG Z L， LI J， LUO Z M， et al. Spectral-Spatial Residual Network for Hyperspectral Image Classification： A 3D Deep Learning Framework ［J］. IEEE Transactions on Geoscience and Remote Sensing， 2017， 56（2）： 847-858.

［20］WANG F， JIANG M， QIAN C， et al. Residual Attention Network for Image Classification ［C］//2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2017： 6450-6458.

［21］WU Z H， PAN S K， CHEN F W， et al. A Comprehensive Survey on Graph Neural Networks ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2020， 32（1）： 4-24.

［22］BRUNA J， ZAREMBA W， SZLAM A， et al. Spectral Networks and Locally Connected Networks on Graphs ［EB/OL］. （2013-12-22）［2023-01-01］. https：//arxiv.org/abs/1312.6203.

［23］KIPF T N， WELLING M. Semi-supervised Classification with Graph Convolutional Networks ［EB/OL］. （2016-09-09）［2023-02-10］. https：//arxiv.org/abs/1609.02907.

［24］VELIKOVIC P， CUCURULL G， CASANOVA A， et al. Graph Attention Networks ［EB/OL］. （2017-10-30）［2023-02-15］. https：//arxiv.org/abs/1710.10903.

［25］WANG T， WANG G， TAN K E， et al. Spectral Pyramid Graph Attention Network for Hyperspectral Image Classification ［EB/OL］. （2020-01-20）［2023-03-01］. https：//arxiv.org/abs/2001.07108.

［26］SHA A S， WANG B， WU X F， et al. Semisupervised Classification for Hyperspectral Images Using Graph Attention Networks ［J］. IEEE Geoscience and Remote Sensing Letters， 2020， 18（1）： 157-161.

［27］WANG M R， LIU X B， GAO Y X， et al. Superpixel Segmentation： A Benchmark ［J］. Signal Processing： Image Communication， 2017， 56： 28-39.

［28］YING X. An Overview of Overfitting and Its Solutions ［J］. Journal of Physics： Conference Series， 2019， 1168： 022022-1-022022-7.

［29］ZHANG S X， MA Z H， ZHANG G， et al. Semantic Image Segmentation with Deep Convolutional Neural Networks and Quick Shift ［J］. Symmetry， 2020， 12（3）： 427-1-427-11.

［30］COMANICIU D， MEER P. Mean Shift Analysis and Applications ［C］//Proceedings of the Seventh IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 1999： 1197-1203.

（責任编辑： 韩 啸）

收稿日期： 2023-05-04.

第一作者简介： 高路尧（1998—）， 男， 汉族， 硕士研究生， 从事高光谱成像及图像处理的研究， E-mail： gaoluyao20@mails.ucas.ac.cn.

通信作者简介： 胡长虹（1983—）， 男， 汉族， 博士， 副研究员， 从事高光谱成像技术的研究， E-mail： changhonghu@rocketmail.com.

基金项目： 吉林省与中国科学院科技合作高技术产业化项目（批准号： 2020SYHZ0028）和2021年吉林省预算内基本建设基金（批准号： 2021C045-3）.