一类肿瘤-免疫模型的稳定性与Hopf分支分析

赵浛弛　李杰梅

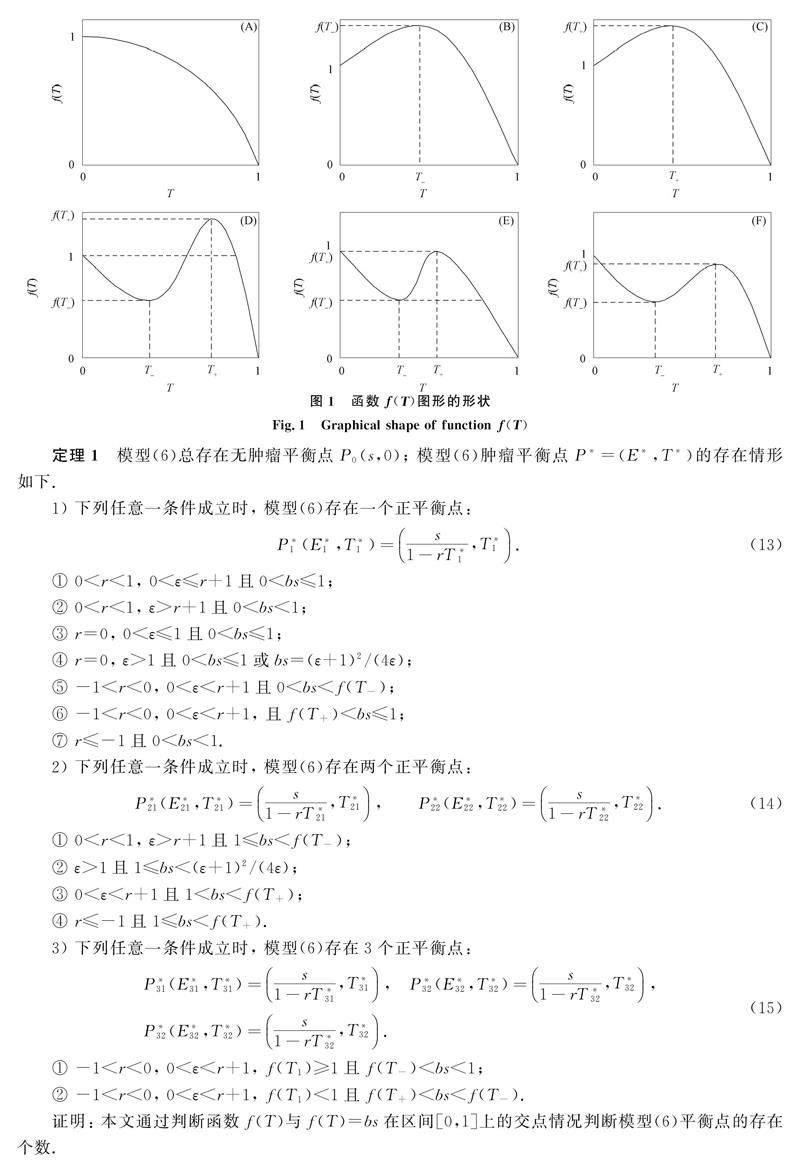
摘要： 考慮一类肿瘤-免疫模型， 讨论其平衡点的存在性条件， 并利用特征方程分析各平衡点的局部动力学稳定性， 证明该模型在相应条件下会发生Hopf分支. 通过计算第一Lyapunov系数得出： 如果系数不为零， 则模型发生Hopf分岔; 如果系数小于零， 则分岔是超临界的; 如果系数大于零， 则分岔是次临界的. 最后利用数值模拟验证理论分析结果.

关键词： 肿瘤-免疫模型； 稳定性； Hopf分支； 超临界； 次临界

中图分类号： O175文献标志码： A文章编号： 1671-5489（2024）02-0189-08

Stability and Hopf Bifurcation Analysis ofa Class of Tumor-Immune Models

ZHAO Hanchi， LI Jiemei

（School of Mathematics and Physics， Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract： We considered a  class of tumor-immune model， discussed the existence  conditions  of their equilibrium points， and used characteristic equations to analyze  the local kinetic stability of each equilibrium point，  proving that the model underwent Hopf bifurcation under the corresponding conditions. By calculating the first Lyapunov coefficient， it can be concluded that if the coefficient is not zero， the model undergoes Hopf bifurcation，  the bifurcation is supercritical if the coefficient is less than zero， and the bifurcation is subcritical if the coefficient is greater than zero. Finally， numerical simulations are used to validate the theoretical analysis results.

Keywords： tumor-immune model; stability; Hopf bifurcation; supercritical； subcritical

0 引 言

癌症是威胁人类生命的一种重大疾病， 如何用科学方法对癌症进行预防和治疗已成为全球最重要的公共卫生问题之一［1］. 中国癌症中心最新数据表明， 2016年中国新增癌症病例约406.4万例， 新增癌症死亡病例241.35万例［2-3］. 目前癌症的临床治疗主要以手术治疗、 化学治疗和放射治疗为主. 这些治疗方法各有优势， 但由于其严重的副作用， 给患者的生活质量和生命带来巨大威胁［4］. 免疫疗法目前已成为治疗癌症的重要组成部分， 免疫疗法的目标是通过增强免疫系统的有效性加强患者自身对抗癌症的天然能力， 免疫系统在对抗癌症中的重要性已在实验室和临床中得到验证［5-6］. 研究表明， 通过建立并分析肿瘤细胞和免疫系统相互作用的数学模型可更好地了解肿瘤的发生和发展机理［7-9］.

Kuznetsov等［10］假设肿瘤细胞对效应细胞具有双线性抑制率和饱和刺激率， 建立了数学模型：dE/dt=s+pET/g+T-mET-dE，dT/dt=aT（1-bT）-nET，（1）其中E（t）和T（t）分别表示效应细胞和肿瘤细胞在t时刻的浓度. 文献［10］讨论了模型（1）平衡点的存在性和稳定性， 计算了该模型的局部分岔和全局分岔的阈值， 预测了肿瘤的增长过程及其临床表现， 发现肿瘤一般具有3～4个月周期的复发特征.

参考文献

［1］FREDDIE B， AHMEDIN J， NATHAN G， et al. Global Cancer  Transitions According to the Human Development Index （2008—2030）： A Population Based Study ［J］. Lancet Oncology， 2012， 13（8）： 790-801.

［2］李纪宾， 邹小农. 《2016年中国癌症发病和死亡情况》解析 ［J］. 环境卫生学杂志， 2023， 13（1）： 45-47. （LI J B， ZOU X N. Interpretation of Cancer Incidence and Mortality in China， 2016 ［J］. Journal of Environmental Hygiene， 2023， 13（1）： 45-47.）

［3］ZHENG R S， ZHANG S W， ZENG H M， et al. Cancer Incidence and Mortality in China， 2016 ［J］. Journal of the National Cancer Center， 2022， 2（1）： 1-9.

［4］ELADDADI A， KIM P，  MALLET D. Mathematical Models of Tumor-Immune System Dynamics ［M］//Proceedings in Mathematics & Statistics， Vol.107. New York： Springer， 2014： 59-108.

［5］STPHANIE C， ERIC V. Chemotherapy and Tumor Immunity ［J］. Science， 2018， 362： 1355-1356.

［6］KATSUTA E， RASHID O M， TAKABE K. Clinical Relevance of Tumor Microenvironment： Immune Cells，Vessels and Mouse Models ［J］. Human Cell， 2020， 33（4）： 930-937.

［7］DE PILLIS L G， ELADDADI A， RADUNSKAYA A E. Modeling Cancer-Immune Responses to Therapy ［J］. Journal of Pharmacokinetics and Pharmacodynamics， 2014， 41（5）： 461-478.

［8］EFTIMIE R， BRAMSON J L， EARN D J D. Interactions between the Immune System and Cancer： A Brief Review of Non-spatial Mat-hematical Models ［J］. Bulletin of Mathematical Biology， 2011， 73（1）： 2-32.

［9］DE PILLIS L， FISTER K R， GU W Q， et al. Mathematical Model Creation for Cancer Chemo Immunotherapy ［J］. Computational and Mathematical Methods in Medicine， 2009， 10（3）： 165-184.

［10］[JP2]KUZNETSOV V A， MAKALKIN I A， TAYLOR M A， et al. Nonlinear Dynamics of Immunogenic Tumors： Parameter Estimation and Global Bifurcation Analysis ［J］. Bulletin of Mathematical Biology， 1994， 56（2）： 295-321.[JP]

［11］GALACH M. Dynamics of the Tumor-Immune System Competition： The Effect of Time Delay ［J］. International Journal of Applied Mathematics & Computer Science， 2003， 13（3）： 395-406.

［12］LI J Q， XIE X， CHEN Y M， et al. Complex Dynamics of a Tumor-Immune System with Antigenicity ［J］. Applied Mathematics and Computation， 2021， 400： 126052-1-126052-25.

（責任编辑：  赵立芹）

收稿日期： 2023-06-12.

第一作者简介： 赵浛弛（1994—）， 女， 汉族， 硕士研究生， 从事非线性微分方程动力学的研究， E-mail： zhaohanchi94@163.com.

基金项目： 国家自然科学基金（批准号： 11801243）.