2024年普通高等学校招生全国统一考试模拟试卷数学(全国甲卷)
巨小鹏


(本试卷满分150分,考试用时120分钟)
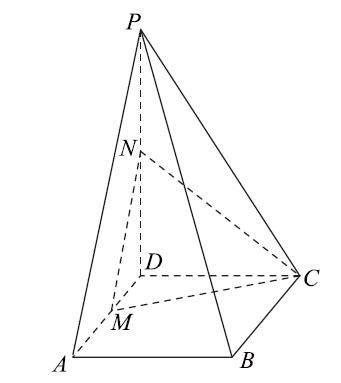
18.如图所示,在四棱锥PGABCD 中,PD =2AD ,PD ⊥DA ,PD ⊥DC,底面ABCD 为正方形,M ,N 分别为AD ,PD 的中点.
(1)求证:PA ∥平面MNC;
(2)求直线PB 与平面MNC 所成角的正弦值.
19.某村从事以紫长茄为主的蔬菜种植.受种植条件、管理水平、市场等因素影响,每年紫长茄的平均亩产量和统一收购价格会有波动,亩产量与收购价格互不影响.根据以往资料预测,该村紫长茄今年的平均亩产量X (单位:吨)的分布列如下表所示.
紫长茄今年的平均统一收购价格Y(单位:万元/吨)的分布列如下表所示.
(1)某农户种植三个大棚紫长茄,每个大棚1亩,每个大棚产量相互独立,求这三个大棚今年总产量不低于34吨的概率;
(2)紫長茄今年每亩种植成本约15万元,设Z 表示该村紫长茄今年平均每亩的利润(单位:万元),求Z 的分布列和数学期望.
20.已知抛物线C 的顶点在原点,焦点在坐标轴上,点A(1,2)为抛物线C 上一点.
(1)求C 的方程;
(2)若点B(1,-2)在C 上,过B 作C 的两弦BP 与BQ,若kBP kBQ =-2,求证:直线PQ 过定点.
21.已知函数f(x)=ex -e-x ,g(x)=ax,其中a∈R.
(1)试讨论函数F(x)=f(x)-g(x)的单调性.
(2)当a=2时,记函数f(x),g(x)的图像分别为曲线C1,C2.在C2 上取点Pn(xn ,yn)作x 轴的垂线交C1于Qn ,再过点Qn 作y 轴的垂线交C2 于Pn+1(xn+1,yn+1)(n∈N? ),且x1=1.
(ⅰ)用xn 表示xn+1;
(ⅱ)设数列{xn}和{lnxn}的前n 项和分别为Sn ,Tn ,求证:Sn -Tn+1>nln2.

