基于混沌理论的非饱和土含水率预测

朱悦璐 吴奇俞

摘要：针对无资料区土体含水率数据难以获取的问题，提出了一种基于卫星反演-相空间重构-非饱和入渗计算的组合方案，以研究区110 d土体表层含水率为基础，预测未来100 d无资料时段土体表层及内部含水率分布规律。计算结果表明：研究区含水率时间序列具备混沌特征，可由一维时间序列拓扑为一个嵌入维数m=5，迟滞τ=10的相空间，由该相空间预测的土体表层含水率在验证期最小相对误差为0.7%，最大相对误差为2.4%，在预测期最小相对误差为2.2%，最大相对误差为8.3%，均满足工程需求，因此将其用于后续非饱和入渗计算的边界条件是真实有效的。该方案具有動力学特性和物理力学意义，可为无资料地区土体含水率估计借鉴。

关键词：土体含水率； 非饱和入渗； 相空间重构； 混沌理论； Richards方程； 非饱和土

中图法分类号： TU43

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.04.028

0引 言

基于事物已有信息准确预测未来发展趋势，一直以来都是科学探索最前沿的目标之一［1-3］。在土壤水领域，预测土体表层及内部含水率变化规律，是进一步探索陆气水量交换［4］、地下水动力学［5］、非饱和土力学［6］等很多相关课题的基础，在工程中具有重要意义。

现阶段，一种获取长时间序列某区域土体含水率的有效手段，是通过大尺度卫星遥感技术（例如高分5号光谱卫星［7］、GF-1多光谱卫星［8］、Sentinel -2卫星等［9］），反演逐日土体表层含水率数据，经整合处理后，最终生成高分辨率含水率数据库。但受传感器或轨道限制，现有的深空卫星探测技术均存在卫星扫描盲区（固定时段盲区或固定位置盲区），因此无法避免数据库中出现资料不连续的时段，即无资料区，当研究区无资料时段过多时，数据库可信度就会下降，从而大大降低预测的精度。

现有针对无资料区含水率的数据修复，可分为野外单点实测和室内数值模拟。传统的野外监测虽然精度较高，但同时亦具有成本高、耗时长、数据同步性差等缺点；而室内数值模拟，大多通过统计手段插补无资料区表层土体含水率数据，再基于机器学习构建不同深度的土体内部含水率模型［10-11］，这导致预测结果大多仅具备统计意义而缺乏物理力学依据。

基于此，本次研究以卫星反演生成的土体表层含水率数据库为基础，通过相空间重构预测方法［12-14］，将一维含水率时间序列拓扑为高维相空间，在相空间内对无资料区土体表层含水率进行非线性动力学预测，并将预测结果代入非饱和入渗控制方程，最终构建土体内部含水率变化规律。相比于传统研究，该方案土体表层含水率预测结果是基于实测数据的动力学反演，具备物理意义；土体内部含水率预测结果是基于非饱和入渗控制方程迭代计算，具备力学意义。

1研究数据及区域

1.1全球卫星反演数据库

本次研究以SMAP卫星（Soil Moisture Active Passive）与AMSR-E（Advanced Microwave Scanning Radiometer）系列传感器所获的2002～2020年土体表层0～5 cm逐日全球高精度、长系列含水率（NNsm）为基础数据集，其空间分辨率精度为0.3°×0.3°经纬度，数据来源于“国家青藏高原科学数据中心”（http：∥data.tpdc.ac.cn）。

1.2本研究计算数据集

研究区地理中心坐标为N34°22′55″，E107°17′01″，位于中国陕西省宝鸡市远郊，人类活动影响因素较弱。经资料分析，该地区受气象条件、云层遮挡等因素影响，存在数据间断性缺失，符合无资料区特征。具体计算中，选择无资料时段前具有一段完整数据的时段，作为基础数据集。若基础数据集选择过短，会导致相空间重构不准，而基础数据集选择过长，则会导致计算复杂度呈几何倍数增长。基于以上原因，本次研究选取2020年第103～212天连续110组数据作为计算序列x（t），213～227天15组数据作为验证序列，如表1所列。前人研究成果表明，这一长度的序列可满足相空间重构相关要求［15］。

2研究方法

本次研究预测无资料区土体剖面含水率的具体步骤为：① 通过相空间重构，将一维含水率时间序列θ（t）拓扑为高维相空间，在相空间内对土体表层含水率展开预测；② 将预测结果作为未来第一日土体边界含水率θ01，结合测定的初始含水率θi1，代入入渗控制方程，计算第一日入渗曲线θ（z，t）；③ 当t=24 h时，对应的含水率曲线即为第二日土体初始含水率θi2；再结合相空间内逐步预测的第二日表层含水率θ02，作为第三日计算基础；④ 重复以上步骤，即可建立未来时期无资料地区土体剖面含水率预测模型。迭代计算示意如图1所示。

2.1一维时间序列相空间重构

对于一组一维时间序列x（t），t=1，2，…n，Packard等［16］提出一种相空间重构方法，若该序列具有混沌特性，则可通过引入嵌入维数m和迟滞时间τ，将一维时间序列扩展成多维相空间，以此为基础预测原时间序列。一个标准的一维时间序列相空间重构如式（1）所示。

当m、τ均取（2，1）时，按照式（1）重构规则，上述一维时间序列演化为一个二维相空间，其坐标依次为（17.3，19.2），（19.2，16.7），（1.67，12.4）…，相点在二维相空间（x，y）的移动轨迹如图3所示。

同理，当m、τ均取（3，2）时，上述二维相空间进一步变化为三维相空间，其坐标依次为（17.3，19.2，16.7），（19.2，16.7，12.4），（16.7，12.4，18.3）…，相点在三维相空间（x，y，z）的移动轨迹如图4所示。

在更高的维度下，相点分布及移动轨迹已不能用坐标系直观描述，但可通过数学计算求解。当系统坐标确定、演化轨迹已知时（例如图中箭头方向），即可根据演化轨迹对系统未来发展做出预测，显然不同的嵌入维数m和迟滞τ所构成的相空间包含的信息不同，因此如何选择合理的重构参数十分重要，以下小节将对这一内容具体讨论。

2.2相空间参数及混沌特性判断

2.2.1迟滞τ计算

对于延迟时间的选择，常用的手段为式（2）所示的自相关系数法，通过计算序列在不同延迟时间k=1，2…下的自相关系数rk，当自相关系数rk第一次接近于0时，所对应的延迟时间k即定义为迟滞τ。

2.2.2混沌特性判断

只有具备混沌特性的序列，相空间重构才有意义。最常见的混沌特性判别法为G-P算法［18］，即识别时间序列是否具有饱和关联维数D2（m），具体计算方案为：任取一m（实际操作中一般从m=2向后连续取自然数），将m、τ代入式（1）生成一个相空间，在该相空间中，人为设定一个r值且满足r>0。

由式（3）、（4）及Heaviside函数定义可知，Cmr的含义为相空间内两个相点距离小于r的概率。求得Cmr后，计算lnCmr和lnr，二者是一组确定的常数。由小到大重复设定不同的r值代入（3）式计算，在lnCr-lnr坐标系中拟合曲线，此时曲线的直线段斜率即为关联维数D2。

重新选择不同的m，重复以上步骤，计算D2，若随着m的增加，D2-m拟合曲线有水平渐近线，则表明原时间序列具有混沌特性；若随着m增加，D2一直增加（或减小），拟合曲线无渐近线，则认为原时间序列为一随机序列，不具备混沌特性。

2.2.3嵌入维数m计算

若经过判断，时间序列具有混沌特性，则可取D2不再增加时所对应的m为重构相空间的嵌入维数。当最终参数m、τ确定后，即将原一维时间序列x（t）扩展成一个m维相空间，此时可在该相空间内，对原序列进行预测。

2.3相空间重构数据预测

本文采用局部相点平均法对生成的相空间预测［20］，在式（1）所表达的相空间中，最后一个相点（最后一列）Xn的下一步演化结果显然受到临近相点的影响。因此，可寻找与Xn最接近的若干个相点，以这些相点下一步演化结果的平均值作为Xn的演化结果，记作Xn+1；新相点对应向量最后一个分量xn+1即为原时间序列在t+1时刻的预测值。局部相点平均预测法原理如图5（a）所示，算法如图5（b）所示。图中与Xn距离最近的3个相点分别为Xp、Xq、Xl，它们下一步演化为Xp+1、Xq+1、Xl+1，演化后相点平均值即为Xn的演化结果Xn+1。

在实际计算中，可采用式（4）计算相空间中每一列与最后一列的距离，并找出距离最短的若干列，用这些列对应的下一列取平均值，即为新相点Xn+1，该新相点即为预测结果。以图5（b）所示为例，新相点计算公式为

2.4非饱和入渗曲线迭代计算

预测得到的研究区土体表层含水率数据，即可作非饱和入渗迭代初始条件代入Richards方程进行计算。该方程是研究非饱和土入渗的重要工具之一，在一定程度上可以揭示非饱和土入渗的主要特征，在非饱和土计算领域应用广泛［21］。本文仅针对第一类边界条件展开探讨，其控制方程及边界条件、初始条件如下［22］：

3模型计算结果

3.1混沌方案预测表层土壤含水率

3.1.1迟滞计算

以式（2）计算表1含水率序列各阶自相关系数，计算结果如图6（a）所示，选取自相关系数第一次接近0时对应的τ作为系统迟滞，由图中可以看出，各阶自相关系数随时间t呈现波动状态，当t=10时，r10=0.134 1第一次接近于0，故本系统迟滞取τ=10。

3.1.2混沌特性判定及嵌入维数的选择

本文选用嵌入维数m=2～10，应用G-P算法进行试算，代入式（3）～（4），在假设不同的m下变换r值，生成一组lnCr-lnr曲线，如图7所示。

从图中可以看出，m取不同值时，各曲线均存在直线段（图中方框区域），且随着m的增加，直线段倾角不断增大，但均未超过斜率为tan 64°的渐近线，为更清晰表征这一特征，绘制直线段斜率D2与嵌入维数m关系曲线如图6（b）。从图中可以看出，D2-m曲线有水平渐近线D2=2.068，這表明关联维数D2不会随着m的增大一直增大，序列具有混沌特性，因此可取D2趋于稳定时对应的m=5为系统的最终嵌入维数。

3.1.3相空间重构及预测

以含水率时间序列x（t）、τ=10、m=5，应用式（1）重构相空间，重构的含水率相空间共有n-m-1τ=110-5-1×10=70个相点，每个相点有m=5个分维。即该相空间是一个5行70列矩阵。限于篇幅所限，本文仅按照重构规则，罗列第1，15，30，50，70号相点，以供读者检验。

上述5个影响相点经过一步演化后的相点为X59、X69、X63、X30、X49，如式（10）所示。

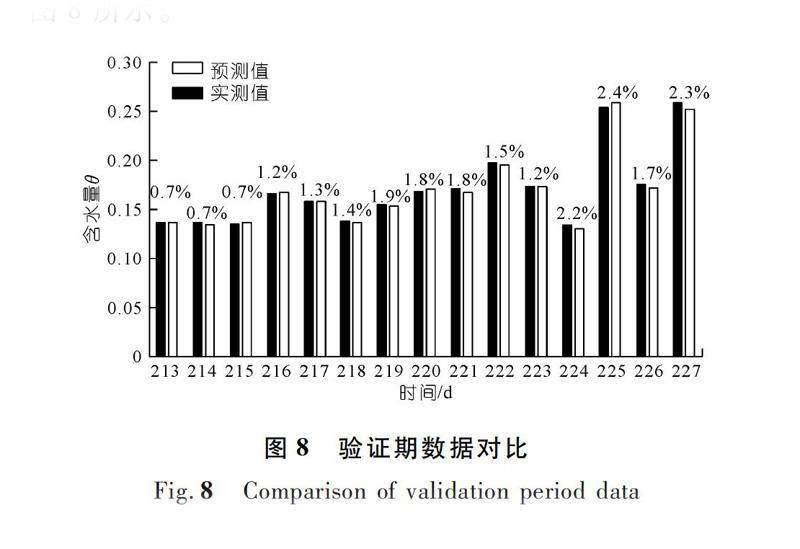
表1数据库可知，这一区域含水率在2020年第213天（即t=111时刻），含水率为0.136 7，当取本文研究精度小数点后3位时，预测值与实测值在千分位上精确一致。采用同样方法，预测未来15 d含水率数据，并与第213～227天的验证序列进行对比，对每组数据，采用工程中常用的相对误差公式进行计算，其结果如图8所示。

可以看出，在验证期的15组数据中，预测值与实测值最大相对误差为2.4%（第225 d），最小相对误差为0.7%（第213，214，215 d），对于一般工程，可以认为该精度可以满足工程需求。重复以上步骤，计算未来100 d土体表层含水率数据，如图9所示。

由图9可以看出，在预测期内，大部分时段实测数据缺失，但在第12天、27天、45天、78天、94天仍有卫星反演数据，将这些数据作为实测值应用相对误差公式与预测值进行对比，其整理结果如表2所示。

通过表2最后一列相对误差变化趋势可以看出，在预测期内，预测误差随着日期延长，呈现波动上升趋势，这表明预测精度有所下降，但尽管如此，最大相对误差仍仅为8.3%（预测期第94 d），仍小于一般工程中含水率预测精度在10%以内的要求。因此可以认为，在预测区间，基于相空间重构的含水率表层预测方案可用于工程实际，同时也可以认为，其作为后续逐日非饱和入渗计算的边界条件是真实有效的。

3.2土体含水率剖面迭代计算

本文计算中，土体初始含水率为0.037，以3.1小节所计算的t=111 d土体表层含水率预测值0.137作为起始时刻边界含水率，其余参数见表3；计算第一日不同时段t不同深度z处的含水率，表3中仅罗列t=480 min时刻，0～80 cm深度处含水率计算数据以供验证，其余数据类似，不再赘述。

将表3计算成果绘制成一簇曲线，如图10（a）所示。当t=1 440 min（t=24 h）时，所对应的曲线即为第一天入渗结束时，0～80 cm处土体含水率分布，该含水率剖面分布，即可作为第二日土体初始含水率，而第二日边界含水率为3.1小节应用相空间重构预测的第二日表层含水率，将二者继续代入式（7），即可迭代计算出第二日非饱和入渗曲线，如图10（b）所示。

重复上述步骤，即可获得未来连续100 d土体非饱和含水率分布曲线，这些曲线即构成土体含水率剖面分布模型；限于篇幅，第3～100天类型重复图片不再罗列。通过图集，即可方便获取未来100 d内任意时刻、任意位置的土体含水率分布。

3.3讨 论

通过以上小节内容可知，应用本文方法，可以方便预测未来时段，无资料地区表层含水率分布和土体内部含水率分布，但仍有两个问题需要进一步讨论说明：

（1） 在混沌预测表层含水率的方案中，本次研究仅采用基础的“局部相点法”进行预测，其余例如基于Lyapunov指数预测法、基于关联维数D2预测法等其他混沌预测方法，由于篇幅所限本文并未采用。

（2） 在非饱和入渗计算中，为更清晰展现本研究思路，文章仅采用最为广泛的一种Richards方程解析解进行迭代，并未使用例如Hydrus-1D/2D/3D系列数值计算软件进模拟，但这同样并不妨碍本文的主旨和结论。

4结 论

本文提出了一种无资料区土体表层及内部含水率的预测方案，结合相空间重构理论与非饱和入渗控制方程，计算生成了未来100 d内土体0～80 cm深度的含水率分布，预测结果表明，在验证期和预测期，含水率预测值与实测值最大相对误差分别为2.4%和8.3%，满足工程精度，以该预测结果计算的土体剖面含水率模型真实可靠。

按照本文步骤，可以复现任意研究区土体含水率潜在分布状态，对于估计无资料地区土体含水率在长时间序列下的变化规律，本方案具有计算简单、无野外作业、成本低等优势，可为相关工程提供一定借鉴。

参考文献：

［1］李彬楠，樊贵盛，申丽霞.基于BP神经网络方法的黄土水分特征曲线预测模型比选［J］.中国农村水利水电，2023（1）：171-175.

［2］詹明强，陈波，刘庭赫，等.基于变权重组合预测模型的混凝土坝变形预测研究［J］.水电能源科学，2022，40（9）：115-119.

［3］吴浩，张金接，姜龙，等.基于灰色理论的边坡变形时效特性预测研究［J］.中国水利水电科学研究院学报，2014，12（3）：270-275.

［4］刘艺朦，魏江峰，赵景文.WRF 4.0模式陆气耦合对不同物理参数化方案的敏感性初探［J］.大气科学学报，2023：46（3）：431-440.

［5］陆培榕，罗纨，贾忠华，等.HYDRUS数值模拟方法在土壤水动力学实验教学中的应用［J］.实验技术与管理，2022，39（11）：173-176.

［6］谢定义.非饱和土力学［M］.北京：高等教育出版社，2015.

［7］曹粤，包妮沙，周斌，等.基于实测光谱和国产高分五号高光谱卫星的铁尾矿表层含水率遥感反演方法研究［J］.光谱学与光谱分析，2023，43（4）：1225-1233.

［8］姚一飞，王爽，张珺锐，等.基于GF -1卫星遥感的河套灌区土壤含水率反演模型研究［J］.农业机械学报，2022，53（9）：239-251.

［9］杜瑞麒，陈俊英，张智韬，等.Sentinel-2多光谱卫星遥感反演植被覆盖下的土壤盐分变化［J］.农业工程学报，2021，37（17）：107-115.

［10］ 冀荣华，李鑫，张舒蕾，等.基于时延神经网络的多深度土壤含水率预测［J］.农业工程学报，2017，33（增1）：132-136.

［11］李旭强，郑秀清，薛静，等.基于BAS-BPNN模型的季节性冻融期土壤含水率预测［J］.节水灌溉，2022（10）：66-70.

［12］黄润生，黄浩.混沌及其应用（第二版）［M］.武汉：武汉大学出版社，2005.

［13］王利，岳聪，舒宝，等.基于混沌时间序列的黄土滑坡变形预测方法及应用［J］.地球科学与环境学报，2021，43（5）：917-925.

［14］周翠英，陈恒，朱凤贤.边坡演化的非线性时间序列多元混沌判别［J］.地球科学-中国地质大学学报，2008，33（3）：393-398.

［15］YANO M，HOMMA N，SAKAI M，et al.Phase-space reconstruction from observed time series using Lyapunov spectrum analysis［C］∥Proceeding of SICE Annual Conference 2002.Osaka（Japan）：SICE，2002，721-726.

［16］PACKARD N H，CRUTCHFIELD J P，FARMER J D，et，al.Geometry from a time series［J］.Physical Review Letters，1980，45（9）：712-716.

［17］罗哲贤，马镜娴.混沌动力学及其在干旱预测中的应用［J］.甘肃气象，1997，15（3）：1-5.

［18］GRASSBERGER P，PROCACCIA I.Measuring the strangeness of strange attractors［J］.Physica D-Nonlinear Phenomena，1983，9（1-2）：189-208.

［19］張恭庆，林源渠.泛函分析讲义［M］.北京：北京大学出版社，2001.

［20］高俊杰.混沌时间序列预测研究及应用［D］.上海：上海交通大学，2013.

［21］朱悦璐，陈磊.基于最小作用原理的Richards方程变分解［J］.岩土力学，2022，43（1）：119-126.

［22］ZHU Y L，XIAO Y T.Research on a key question in the parlange solution［J］.KSCE Journal of Civil Engineering，2021，26：472-781.

［23］雷志栋，杨诗秀，谢森传.土壤水动力学［M］.北京：清华大学出版社，1988.

（编辑：黄文晋）