基于统计学内容与特征分析的通信信息自动化检测系统研究
鲁 勇
(国网山南供电公司,西藏 山南 856000)
0 引 言
随着信息技术的快速发展,互联网已成为人们日常生活中不可或缺的一部分[1-2]。然而,互联网带来较多安全威胁,如网络钓鱼、网络病毒、网络攻击等[3-4]。为保护通信信息的安全,国内外研究人员陆续研究不同的异常数据检测方法,提出如使用机器学习的自动化检测方法和基于数据经验检测的方法[5]。虽然这些方法取得显著的进展,但仍存在一些不足,如难以抵抗对抗性攻击和实时性较差等。统计学作为一门应用广泛的学科,可以深入理解数据的分布、趋势和异常值。而特征分析法可以提取关键的数据特征,用于训练和改进检测模型。因此,文章以统计学为出发点,通过统计学内容与特征分析来帮助检测系统识别异常的数据模式和行为,从而提高检测的灵敏度[6-7]。文章旨在探讨如何利用统计学和特征分析来提升通信信息自动化检测系统的能力,以更好地应对网络安全威胁。
1 基于网络流量内容属性与特征的多元相关性降维统计分析
统计分析是通过收集、整理和分析数据来找出数据背后的规律、趋势和关系的过程[8-9]。统计分析可以帮助研究并理解数据所代表的现象,并从中得出有关该现象的结论。其方法主要包括描述统计和推断统计2 个类别,分别表示对对象内容和特征的分析。具体的分析手段以多元统计分析、相关性分析和主成分分析(Principal Component Analysis,PCA)为主。多元统计分析研究事物中多个变量之间的相互依赖关系,相关性分析仅研究现象间存在的依存关系,主成分分析则是对事物对象的降维处理,以达到表征性变量分析的目的。网络流量数据中的内容属性指网络流量中的数据包的内容,如协议类型、数据类型、源网际互连协议(Internet Protocol,IP)地址及目标IP 地址等。特征属性指网络流量中的某些特征,如数据包的大小、延迟、带宽等。此外,网络流量是一个具有多维度的统计大类。
针对多元化的网络流量数据,文章利用多元相关性分析来计算网络数据流量的统计量。统计量包含样本均值、样本方差、样本标准差以及协方差。
样本均值的计算式为
样本方差的计算式为
式中:s2表示样本方差。
样本标准差的计算公式为
式中:s表示样本标准差。
协方差的计算式为
结合式(1)~式(4),文章利用蒙特卡洛算法来抽取计算网络流量数据中两属性之间的相关性。该方法的准确性依赖三角形中抽样点的数量,点数越多,估算结果通常越精确。在一个封闭区域内,散落许多流量信息点。随机抽取2 个点,将各自在二维空间中的横纵坐标取对角值,完成后进行数值相乘,即属性特征相乘,然后除以2 得到两点属性相关的三角形面积。三角形的面积计算公式为
式中,和分别表示第i条网络流量中第j个和第k个特征。由此可知,当j=k时,二维空间中两特征处于同一方向位置,夹角为0。此时的面积为0,横纵坐标对角线上的相关点数即为0,表示无相关性。
为求解更高维度的网络流量,研究通过PCA 进行冗余数据剔除和数据降维,PCA 数据标准化的计算公式为
式中:X'表示原始数据;μ表示均值;σ表示标准差。通过式(6)使不同的流量特征具有相同的向量表示。完成数据降维后,将数据输入协方差方程中进行主成分求解,选择其中特征值最大的特征向量。重复该操作,直到将所有的流量数据进行求解,最后构建成一个新的特征空间。
2 基于改进支持向量机的通信信息自动化检测算法
结合降维后的通信数据流量,研究引入支持向量机(Support Vector Machine,SVM)进行具体的流量特征分类工作。SVM 属于一种深受统计学原理和方法影响的机器学习工具,通过这些统计学原理,SVM 能够有效处理高维数据。考虑异常数据特征混入特征数据库会导致流量特征检测性能下降或失败的问题,研究引入孤立森林(Isolation Forest,IF)算法对SVM 进行改进,提出一种孤立森林-支持向量机(Isolation Forest-Support Vector Machine,IF-SVM)分类算法。首先,对输入的流量样本数据进行归一化处理,通过IF 算法计算这些流量数据中的异常点数。其次,通过变更点检测的方式剔除这些异常点。最后,将这些异常点的特征作为标签进行高维空间数据的距离分割[10-11]。该过程中IF 检测流量异常点的公式为
式中:S'i'表示正常流量数据点的个数;x'表示预处理后的初始数据集;n'表示输入数据的大小;s'表示异常数据点的存在概率。由此可知,当S'i'从大到小排序后,其值最小时的s'(x',n')就是异常值。
文章构建基于多元统计相关性降维分析和IFSVM 算法的通信信息自动化检测模型,如图1 所示。

图1 文章设计的通信信息自动化检测模型
由图1 可知,首先获取初始通信流量数据样本,并输入系统进行数据预处理,即数据清洗和数据存储,其次根据流量数据内容和特征分别运用统计学进行统计量计算,并添加多元统计相关性分析和降维分析,最后构建一个流量特征数据库。该数据直接指导后续的流量特征检测,通过IF-SVM 算法对检测流量和特征库流量进行对比检测,以达到数据区分的目的。
3 模型性能测试
文章采用Windows 10 的操作系统,中央处理器(Central Processing Unit,CPU)为Intel Core 2.5 Hz双核,内存为16 GB,利用MATLAB 软件实现建模。引入DARPA IDS 数据集和KDD Cup 1999 数据集作为测试数据来源。两类数据集内容相似,都是用于入侵检测系统的数据集,分别包含约50 000 条和20 000 条网络通信数据,用于研究网络入侵检测和网络安全的相关问题。同时,引入同类型较为流行的数据统计降维方法,如线性判别分析法、因子分析法和独立成分分析法,与文章提出的多元统计相关性降维分析方法进行对比测试。针对相关性降维分析进行对比测试,绘制统计分析空间分布图,如图2 所示。图2(a)为DARPA IDS 数据集数据下的性能测试结果,图2(b)为KDD Cup 1999 数据集数据下的性能测试结果。

图2 不同数据统计降维方法的测试对比结果
由图2 可知,两类数据集下,独立成分分析法的流量数据维度最高,且流量数据多处于高离散程度,该状态表明降维算法可能需要更多的维度来捕获数据的多样性和变化。综合来看,文章提出的多元统计相关性降维分析下的数据内容和数据特征都表现出较优的统计和降维性能,且更适应大数据内容和数据特征的网络信息检测。
为量化信息检测模型的性能效果,研究引入同类型较为流行的检测模型,如朴素贝叶斯模型、阈值模型和支持向量机模型与所提的IF-SVM 模型进行对比。以准确率、召回率、F1值及误报率为测试指标,对这些模型分别进行检测,测试结果如表1 所示。
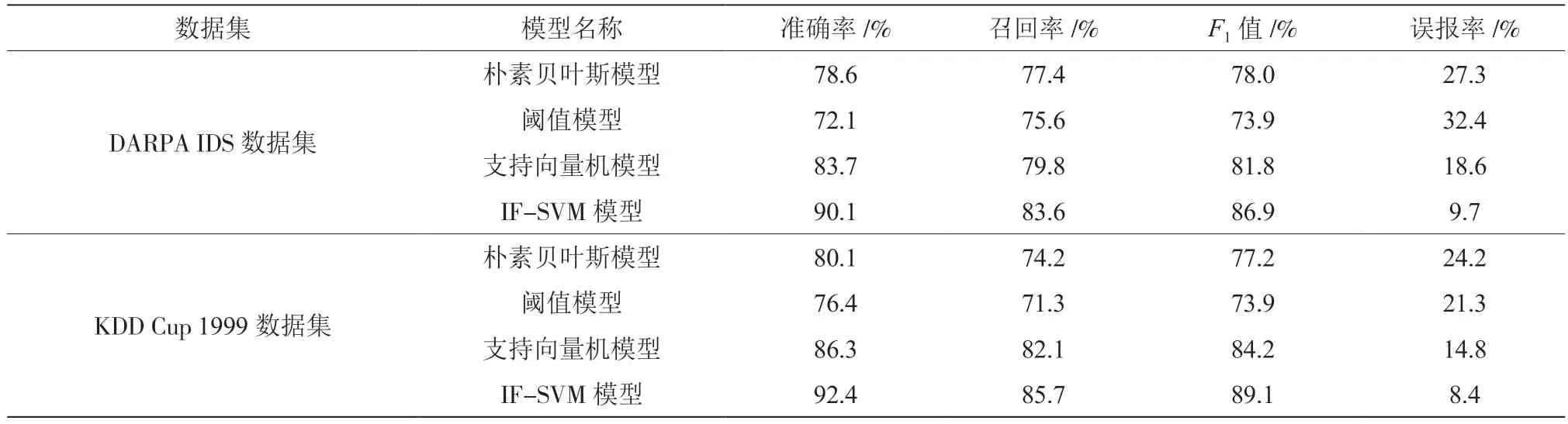
表1 不同通信信息检测模型的指标测试结果
由表1 可知,两类不同的数据集中,综合性能表现最差的是阈值模型,表现最佳的是文章所提的模型。其准确率最高为92.4%,召回率最高为85.7%,F1值最高为89.1%,误报率最低为8.4%。
由图2 内容和表1 数据可知,文章设计的基于多元统计相关性降维分析和IF-SVM 算法通信信息自动化检测模型具有明显的优越性,适合现阶段的通信信息攻击自动化检测。
4 结 论
文章借鉴统计学理论,联合使用统计学理论中的多元统计分析、相关性分析和主成分分析,对通信数据流量进行统计降维,同时引入IF-SVM 分类算法模型,提出一种新型通信信息自动化检测模型。实验结果表明,多元统计相关性降维分析下的数据具有更低的维度和离散程度,数据状态明显优于其他模型。此外,文章所提的IF-SVM 模型的准确率最高为92.4%,召回率最高为85.7%,F1值最高为89.1%,误报率最低为8.4%,远超于同类型较为流行的其他模型。由此表明,文章所提的方法对提高通信信息自动化检测的性能具有正向作用,同时为网络安全领域的进一步研究提供参考。然而,此次研究暂未涉及对该模型的泛化性能测试,后续研究可设置不同的测试环境和条件,以探索该模型的最佳表现。

