基于CDM 理论与SVM 模型的2014-T6 铝合金疲劳寿命预测

高同州，贺小帆，王晓雷，李紫光，朱振涛，詹志新，*

1.北京航空航天大学 航空科学与工程学院，北京 100191

2.北京宇航系统工程研究所，北京 100076

金属材料在航空航天、汽车、民用建筑及生物医学等工程领域中具有广泛应用。这些金属结构在使用过程中常面临循环载荷和恶劣环境的双重考验，进而导致疲劳损伤甚至失效［1-3］。然而，金属疲劳作为一种复杂现象，涉及多个尺度和学科，如材料科学、力学、物理学、化学和工程学等。航空航天领域中，疲劳问题尤为关键，因为航空航天器在极端环境和载荷条件下运行，且需确保其长期可靠性和安全性。复杂的载荷条件和不断变化的操作环境使得疲劳问题愈发复杂［4］。因此，有必要深入研究金属结构疲劳行为的影响因素与机理，建立合适的金属材料的疲劳损伤分析及寿命预测方法。

研究表明，金属结构的疲劳性能对外部和内部因素均非常敏感。外部因素包括零件的形状、尺寸、表面粗糙度和使用工况［5-7］；内部因素则涉及材料成分、微观组织形貌、内部孔隙夹杂等缺陷以及残余应力［8-10］。针对这些方面，已有大量学者进行了深入研究。Zhao等［11］研究了表面粗糙度对铝合金 7075-T6 疲劳强度的影响，且发现由于表面缺陷处的应力集中和裂纹萌生，疲劳强度随着表面粗糙度的增加而降低。该论文还提出了一种基于表面粗糙度和缺陷尺寸预测疲劳强度的改进模型。Zhu等［12］研究了具有不同尺度结构部件的疲劳行为，综述了3 种尺寸效应（统计、几何、技术）及其在金属疲劳方面的研究进展，阐述了统计尺寸效应建模中常用的临界缺陷法和最弱环节法以及考虑几何尺寸效应的高应力体积法。Jiang等［8］研究了不同Gd和Zr 含量的砂铸Mg-Gd-Y-Zr 合金的微观组织、拉伸性能和高周疲劳行为，发现Zr 含量的增加可以增加疲劳强度，而Gd 含量的增加延长了相对高应力下的疲劳寿命。Zhang等［13］从晶体微结构出发结合晶体塑性有限元数值方法研究了增材制造AlSi10Mg 合金的高周和超高周疲劳行为，建立了考虑缺陷效应的Voronoi 曲面细分晶体塑性有限元模型（Crystal Plasticity Finite Element Method，CPFEM）模拟循环塑性变形，采用Morrow 模型和Smith-Watson-Topper（SWT）模型预测疲劳寿命，SWT 模型与CPFEM 模拟表明，孔隙附近的累积循环塑性应变显著高于夹杂物。吴圣川等［14-16］从试验、断裂力学模型以及数值模拟计算等方面深入研究了内部缺陷的形貌、位置、取向等对增材制造AlSi10Mg 疲劳性能的影响。Chiocca等［17］通过数值建模和微观结构分析研究了残余应力对承受完全反向扭转和弯曲载荷的 S355JR 结构钢管板焊接接头疲劳评估的影响，发现在施加扭转载荷时，残余应力对焊接接头的疲劳寿命有影响，在弯曲载荷的情况下没有检测到残余应力的影响。

近年来，多种研究方法被应用于金属结构疲劳性能的探讨，例如经验公式方法［18-20］、临界面法［21］、能量法［22］、相场法［23］和断裂力学方法［24］。除这些方法之外，连续损伤力学（Continuum Damage Mechanics，CDM）方法在金属材料疲劳性能研究中的应用也逐渐增多［25-28］。CDM 将材料失效建模为由微观尺度上的微裂纹、微孔隙的增长及扩散引起的宏观材料性能的逐渐劣化。CDM 可用于模拟金属材料在各种载荷和环境条件下的疲劳性能，预测材料的损伤演化和最终失效。与其他方法相比，CDM 可以解释不同损伤机制之间的相互作用及其对材料特性和行为的影响，捕获损伤累积的非线性和不可逆性质以及其对加载历史的依赖性。然而，CDM 等方法在预测精度方面仍存在不足。

为了提高2014-T6 铝合金材料疲劳寿命预测的准确性，本文基于损伤力学理论与支持向量机模型，建立了一种疲劳寿命预测的新方法。首先，推导了耦合损伤的弹塑性本构模型以及疲劳损伤模型，并给出了理论模型中材料参数的标定方法；其次，提出了基于粒子群算法（Particle Swarm Optimization Algorithm，PSO）的理论模型材料参数的标定方法，获得了本构模型及疲劳损伤模型中的材料参数；然后，基于ABAQUS 平台，通过UMAT子程序的二次开发，实现了疲劳寿命预测的损伤力学有限元数值计算方法，并对2014-T6 铝合金进行了疲劳寿命预测；最后，采用支持向量机（Support Vector Machine，SVM）模型，以CDM 方法的预测误差为训练对象，以此来修正CDM 的预测结果，从而得到更加准确的疲劳寿命预测结果。

1 理论模型

1.1 耦合损伤的弹塑性本构模型

从损伤力学的角度来看，材料内部存在微观不连续性，例如微裂纹和微孔洞等微观缺陷，这些缺陷的萌发和扩展会导致材料性能的劣化。连续损伤力学采用代表性体积单元（Representative Volume Element，RVE）为研究对象，RVE内部材料均匀分布并且其平均物理和力学性能可以描述整个材料的宏观行为。采用损伤变量D来度量材料性能的劣化，损伤变量［29］一般通过RVE 横截面微缺陷面积的占比来进行量化，如式（1）所示：

式中：dA 为RVE横截面积，dAD为dA 中缺陷 的总面积，d为有效承载面积，有效应力与损伤变量的关系如下：

式中：σij为名义应力。

对于损伤耦合的弹塑性本构模型，其中线弹性本构方程为

塑性应变分量的演化率为

1.2 疲劳损伤模型

在多轴加载条件下，基于CDM 的疲劳损伤演化方程为［30］

式中：损伤等效应力σ*(σij)的表达式如下：

在单轴常幅值疲劳载荷条件下，式（7）退化为

式中：σa和σm为单轴循环载荷的应力幅值及应力均值，将公式从D=0 到D=1 积分可以得到单轴循环载荷作用下的疲劳寿命：

2 材料参数标定及数值实现方法

2.1 材料参数标定方法

本文基于粒子群算法（Particle Swarm Optimization，PSO）对本构模型及疲劳损伤模型中的材料参数进行标定。在粒子群算法中，将待求解问题的解空间看作一个“空间”，其中每个解被称为一个“粒子”。每个粒子都有自己的位置和速度，并根据自己的历史最优解和群体最优解来更新自己的位置和速度。其中，历史最优解表示粒子在搜索过程中自己所获得的最优解，而群体最优解表示整个粒子群体在当前迭代中所获得的最优解。通过粒子之间的相互作用和学习，整个群体逐步向最优解靠近。粒子群算法的流程图如图1 所示，具体实现流程如下：

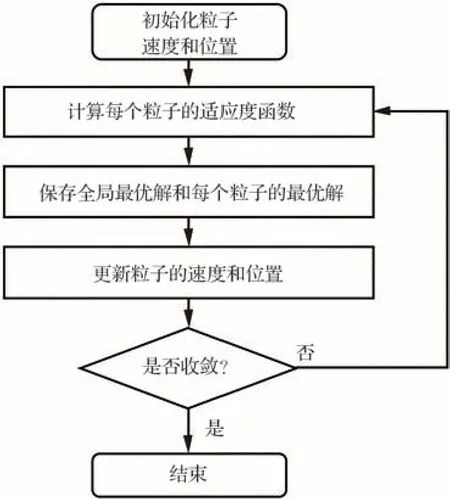
图1 粒子群算法流程图Fig.1 Algorithm flowchart for particle swarm optimization.

1）初始化粒子群：设置粒子群的规模，确定粒子位置和速度的范围，并随机生成粒子位置和速度。

2）评价适应度函数：计算每个粒子的适应度值（目标函数值）。

3）更新最优位置：将当前粒子的适应度值与其历史最优适应度值进行比较，若当前适应度值更优，则更新粒子的个体最优位置。同时，比较粒子的适应度值与群体最优适应度值，若粒子的适应度值更优，则更新群体最优位置。

4）更新粒子速度和位置：对于每个粒子，更新其个体最优位置，即自身历史最优解。如果该粒子的当前位置比之前的位置更优，则将其个体最优位置更新为当前位置。速度更新公式和位置更新公式分别如式（13）和式（14）：

式中：vi(t)表示第i 个粒子在第t 次迭代时的速度，xi(t)表示第i 个粒子在第t 次迭代时的位置，w 为惯性权重，c1和c2分别为个体和群体学习因子，r1和r2是在（0，1）之间的随机数，pi为第i 个粒子的个体最优位置，g 为群体最优位置。

5）终止条件：达到最大迭代次数或满足收敛条件时，停止迭代，否则跳转到第2）步。

6）输出结果：返回全局最优解及其对应的目标函数值。

本文采用2014-T6 铝合金的单轴拉伸应力-应变数据［31］来标定其静力性能参数。在单轴加载条件下，材料的应力-应变曲线关系如式（15）所示，

式中：σy为屈服应力。

在参数标定过程中以试验数据点与本构模型之间的残差平方和为目标函数，使其达到最小。标定得到的本构材料参数如表1 所示，应力-应变数据与本构模型的拟合对比如图2 所示。

表1 2014-T6 的静力性能参数Table 1 Static performance parameters of 2014-T6

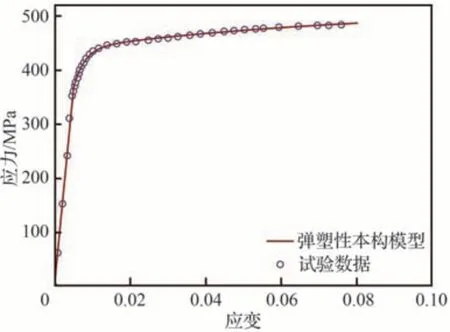
图2 2014-T6 应力应变曲线Fig.2 Stress-strain curve of 2014-T6

对于疲劳损伤演化模型，有α、β、m和n 这4 个材料参数需要标定，采用粒子群算法，采用表2［31］中不同循环载荷下的疲劳试验数据，进行最优参数筛选，最终标定得到的4个材料参数如表3所示，标定后的疲劳损伤模型和试验数据的对比如图3所示。

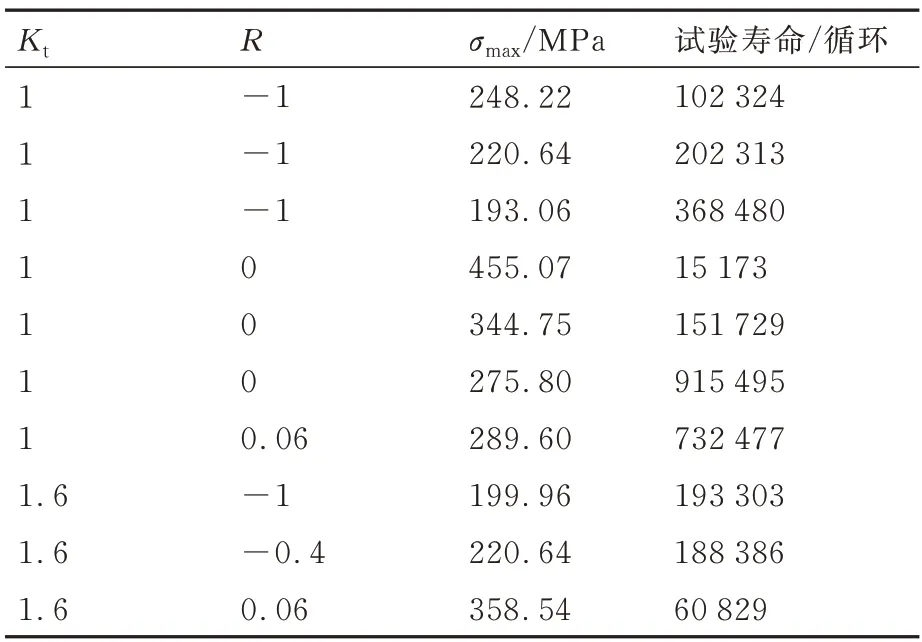
表2 用于标定材料参数的疲劳数据［31］Table 2 Fatigue data for calibration of material parameters［31］

表3 2014-T6 疲劳损伤模型参数Table 3 Fatigue damage parameters of 2014-T6

图3 损伤演化模型与疲劳试验数据对比Fig.3 Comparison between test data and calibrated fatigue model

2.2 疲劳损伤模型的有限元数值实现

本文基于ABAQUS 平台，编写用户自定义材料子程序UMAT，实现了损伤耦合的本构模型以及疲劳损伤模型，通过计算循环载荷下的损伤演化来计算2014-T6 铝合金的疲劳寿命，其数值计算过程如图4 所示。

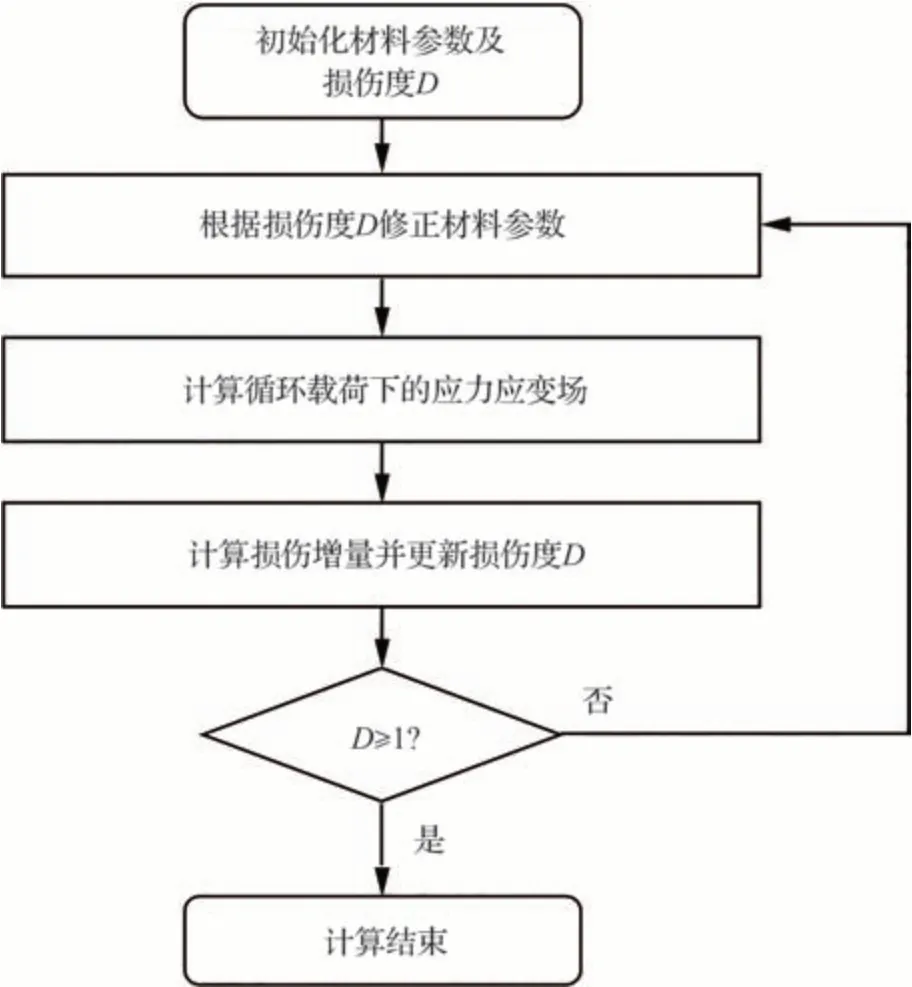
图4 损伤演化数值计算流程Fig.4 Damage evolution numerical calculation flowchart

具体实现流程如下：

1）初始化材料本构参数、损伤演化模型参数和损伤度。

2）根据损伤度更新弹性模量，如式（16）：

3）根据损伤耦合弹塑性本构计算有限元模型各个单元积分点的应力应变场。

4）计算损伤演化速率和损伤增量，更新损伤度，为了减小计算量，采用了跳跃周期法，即认为在ΔN 个周期内损伤演化速率不变：

这里，ΔN 取为试验寿命Nexp的1%。本文分析计算了ΔN 的不同取值对预测结果造成的偏差。选取工况为Kt=1，R=0，σmax=344.75 MPa，试验寿命Nexp=151 729 的数据点，分别计算不同ΔN 下的预测误差，如图5 所示，图中横坐标为ΔN与试验寿命Nexp的比值ΔN/Nexp，可见，当ΔN/Nexp较大时，预测误差较大；随着ΔN/Nexp的减小，预测误差先急剧下降然后逐渐趋于收敛，当ΔN 为试验寿命Nexp的1%时，预测误差约为2%，可以满足疲劳寿命的预测要求。因此，兼顾计算效率和计算精度，本研究取ΔN 为1%的试验寿命Nexp。

图5 预测误差随ΔN/Nexp的变化（Kt=1，R=0，σmax=344.75 MPa，Nexp=151 729）Fig.5 Variation of predicted error with ΔN/Nexp（Kt=1，R=0，σmax=344.75 MPa，Nexp=151 729）

5）判断损伤度是否大于或等于1，是则结束计算认为结构疲劳失效，否则返回第2）步。

2.3 2014-T6 缺口试件疲劳寿命计算

2014-T6 的棒状光滑试件及含缺口试样［32］尺寸图如图6 所示，缺口试样应力集中系数为Kt=1.6。疲劳试验是在300 kg 的Schenck 疲劳试验机上完成，环境为室温、空气条件。加载方式为轴向加载，疲劳载荷为恒幅正弦波载荷，频率范围为18～60 Hz。试样均经过表面机械加工和抛光处理。分别对应力集中系数Kt=1.0 的棒状光滑试件与 Kt=1.6 的棒状缺口试件进行疲劳试验。Kt=1.0时，应力比为R=-1，-0.4，0.06，最大应力的范围为165～455 MPa；Kt=1.6时，应力比为R=-1，-0.4，0.06，0.46，最大应力范围为138～400 MPa。

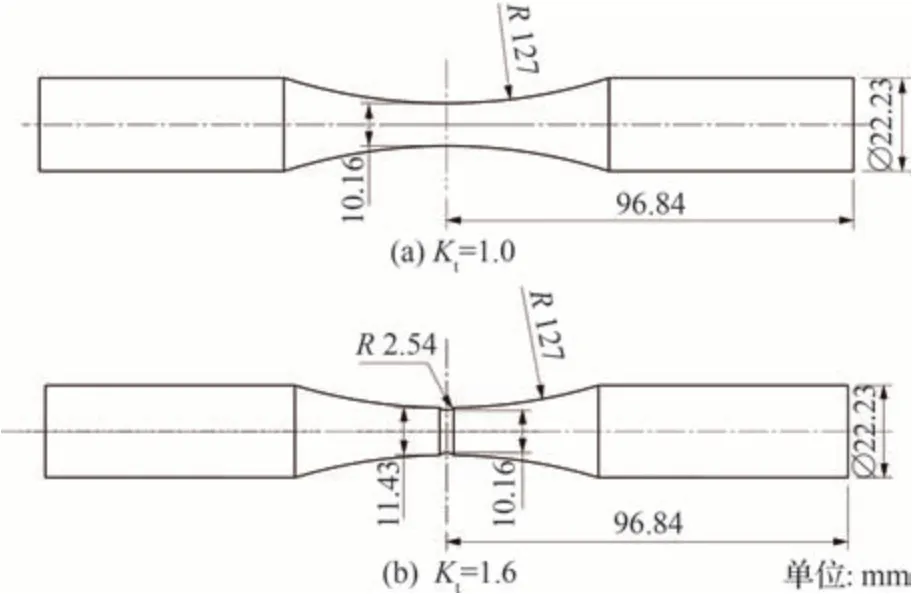
图6 2014-T6 试样尺寸示意图Fig.6 Fatigue test specimen dimensional diagram of 2014-T6

在ABAQUS 平台上建立有限元模型并进行数值计算。考虑到试样的对称性，建立1/8 模型，在3 个对称平面施加对称边界条件，在试样端部施加轴向均匀载荷，如图7 所示。采用了C3D8 八节点线性六面体单元对模型进行网格划分，为了确保计算结果的精度，对缺口周围的局部区域进行了细网格处理，并进行了网格敏感性分析，如表4 所示，以获得独立于有限元网格大小的收敛解。最后，建立的有限元模型中包含了113 418 个单元，缺口处网格尺寸约为0.20 mm×0.07 mm×0.06 mm。

表4 有限元网格敏感性分析Table 4 Sensitivity analysis of finite element mesh

图7 棒状缺口试件1/8 有限元模型和载荷及边界条件示意图Fig.7 Finite element model of 1/8 scale notched round bar specimen and schematic diagram of load and boundary conditions

图8 展示了σmax=200 MPa，R=-1.0时的应力分布云图及损伤度分布云图，可见，缺口边缘应力及损伤度最大，危险点处的损伤度随循环次数的变化曲线如图9 所示，图中表明损伤演化随着循环次数的增加以及损伤度的增大越来越快。危险点处的轴向应力随循环次数的变化曲线如图10，轴向应力-应变曲线如图11，可以看出，随着损伤度的增大，该点的弹性模量逐渐降低导致承载能力越来越弱。

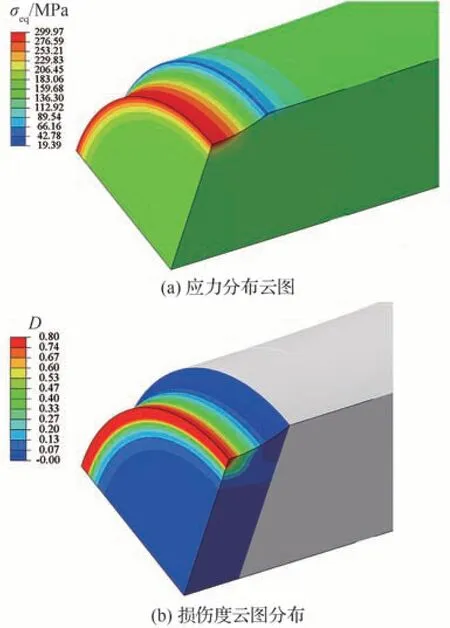
图8 有限元计算结果云图Fig.8 Finite element analysis contour map

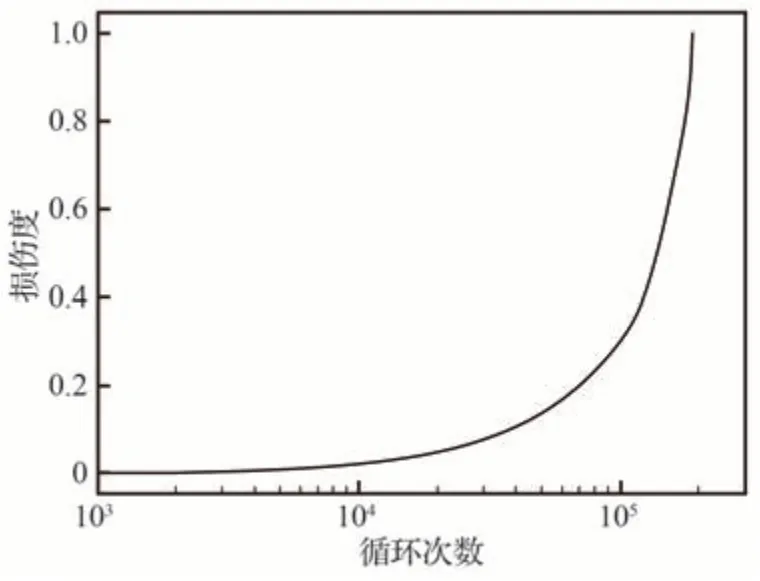
图9 危险截面的损伤度随循环次数变化Fig.9 Variation of damage variable at critical point with the number of cycles

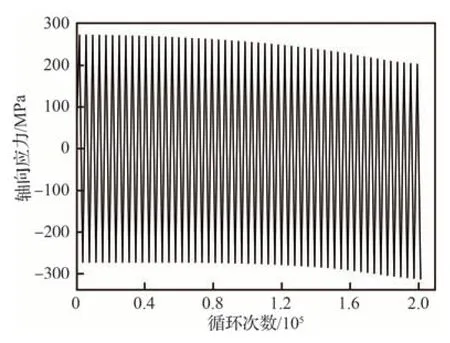
图10 危险点处轴向应力随循环次数的变化Fig.10 Variation of axial stress at critical point with the number of cycles

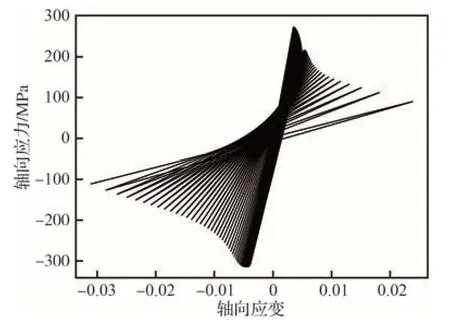
图11 危险点处的轴向应力-应变曲线Fig.11 Axial stress-strain curve at critical point

基于损伤力学有限元数值计算方法，对应力集中系数Kt=1.0 的棒状光滑试样和集中系数Kt=1.6 的棒状缺口件疲劳寿命进行预测，结果如表5 所示，图12 给出了预测结果与试验结果的对比。计算表明，除少数计算结果在3 倍误差带以外，大部分的计算结果都在3 倍误差带以内。此外，材料的微观组织形态、材料制备和材料可能存在的缺陷对材料的疲劳寿命有显著影响，会造成材料疲劳试验数据的分散性。本研究在开展疲劳寿命计算时，所采用的疲劳损伤演化模型中有4 个材料参数α、β、m、n，需要基于材料的疲劳试验数据进行标定，因此，这4 个参数可间接地反映上述因素对材料疲劳性能的影响。

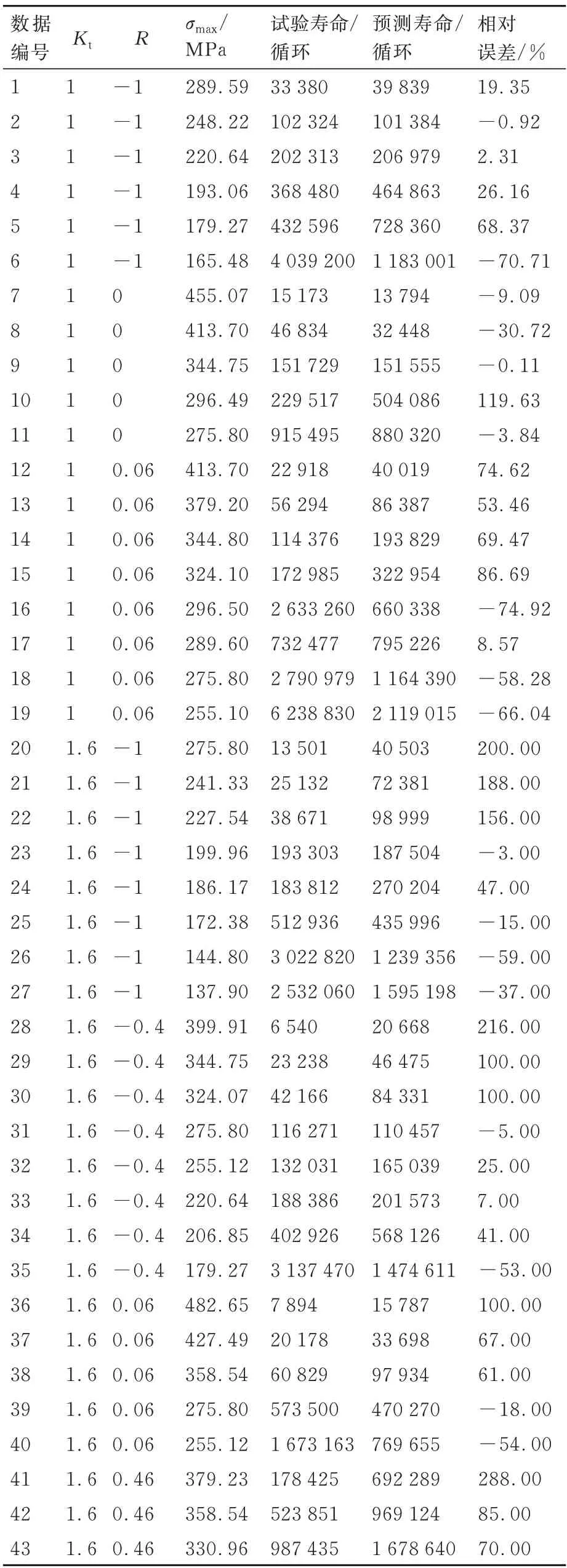
表5 基于损伤力学有限元数值方法的计算结果Table 5 Calculation results of fatigue life based on finite element numerical method of damage mechanics

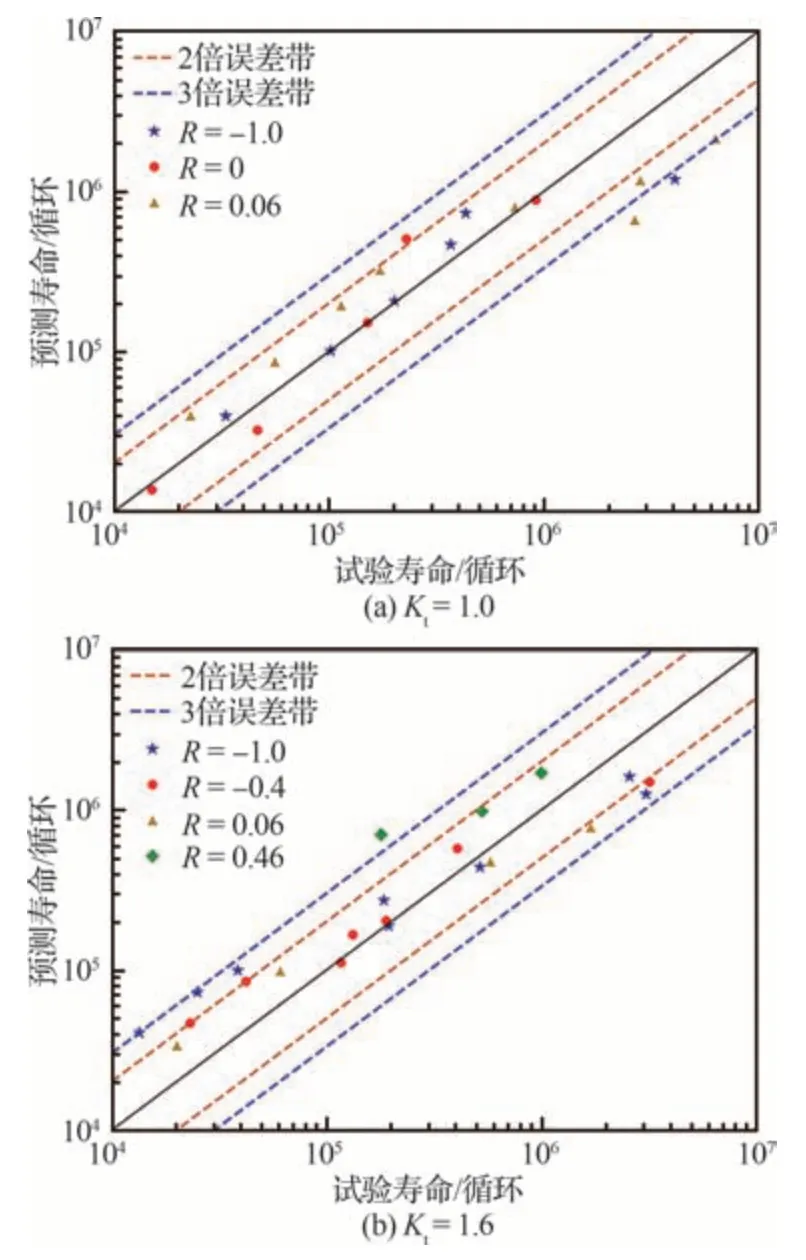
图12 试验寿命与损伤力学数值方法预测寿命对比Fig.12 Comparison of experimental life and life predicted by numerical method of damage mechanics

3 基于损伤力学-支持向量机的疲劳寿命预测方法

尽管疲劳寿命的预测结果在误差带之内，但和试验结果之间仍普遍存在误差，因此采用机器学习方法来修正数值计算结果，以减小误差的影响，提高预测的准确性。本文采用支持向量机（Support Vector Machine，SVM）方法，对基于损伤力学的疲劳寿命预测结果的误差进行训练，从而修正数值预测结果。

3.1 基于误差训练的SVM 模型

SVM 是一种监督学习算法，主要用于分类和回归问题。在回归问题中，SVM 的基本原理是在训练数据之间构建一个最优边界，使得预测误差小于某个指定的阈值，并且使得边界间隔最大化。首先将输入空间映射到一个高维特征空间，然后在该特征空间中找到一个线性函数来逼近目标函数。对一个输入特征向量为xi∈Rd，输出值为yi∈R 的训练 数据集(xi，yi)i=1N，SVM的目标是找到一个线性函数f (x)使得对所有的训练数据f (xi)与yi之间的误差小于ε。在特征空间中，线性函数可以表示为

式中：w ∈Rk是权重向量，ϕ(x)是将x 映射到特征空间的函数，b ∈R 是偏置项；<·，·>表示向量之间的内积。SVM 使得以下目标函数最小化：

其中：‖w‖2是表示正则化项，用于控制模型复杂度；C 是惩罚参数，用于平衡模型复杂度与训练误差和分别为正面松弛变量和负面松弛变量。求解过程中的约束条件为

式中：ε 为容忍度参数。

本文基于误差训练并结合损伤力学方法与SVM 模型对2014-T6 铝合金进行疲劳寿命预测的流程如下：

1）数据收集：获取损伤力学数值方法计算的误差数据建立模型数据库。

2）数据集划分：将数据集划分为训练集、验证集和测试集。

3）参数选择：选择合适的模型及核函数并调整关键参数，本文需要解决的金属疲劳寿命预测问题属于回归分析问题，选择了径向基函数（Radial Basis Function，RBF）核函数。在进行非线性回归问题时，RBF 核函数通过将数据从原始低维空间映射到高维特征空间，能够在高维空间中寻找到数据的非线性关系，使其能够处理复杂的非线性问题。此外，使用RBF 核函数的SVM 具有很强的泛化性能，即使在训练样本较少的情况下，也能得到较好的预测结果。RBF 核函数的表达式为

式中：xi和xj是样本点的特征向量；‖xi-xj‖表示2 个特征向量之间的欧几里得距离；γ 是RBF 核函数的一个参数，通常需要通过交叉验证等方式来确定。

4）模型训练：使用训练集数据训练SVM 模型，通过最小化目标函数来学习最佳的回归超平面。

5）模型评估：使用验证集数据对模型的表现进行评估。

6）预测：利用训练好的模型对测试集数据进行预测。

在本文中，将应力集中系数Kt、应力比R、最大应力σmax作为模型的输入参数，将有限元数值方法的预测误差作为模型的输出参数，进行回归分析。最终，训练得到能够预测损伤力学数值计算方法误差的SVM 机器学习模型。

3.2 模型数据库与预测性能评价指标

机器学习训练过程依赖于大量数据以构建模型数据库。然而，试验数据有限，因此需要通过其他途径扩充数据源。为此，综合利用了疲劳寿命数据的分布特性以及S-N 曲线，随机生成了不同应力集中系数、不同应力比和不同应力水平下的疲劳寿命数据点作为试验数据。

本文在进行数据扩充时，认为在相同的应力比和应力水平下疲劳试验寿命呈正态分布，考虑到S-N 曲线代表了疲劳数据的中值寿命，即对数平均值寿命，因此，本文以给定应力比下所有真实试验数据点与S-N 曲线的偏差平方的平均值作为方差，以给定应力比和应力水平下S-N 曲线的计算疲劳寿命作为当前应力水平下正态分布的均值，进而在每个应力水平下随机生成符合正态分布的疲劳寿命作为扩充数据。扩充数据、真实试验数据集及S-N 曲线对比如图13 所示。可见，扩充数据随机均匀地分布于S-N 曲线两侧。由于S-N 曲线代表了随机数据的均值，扩充生成的数据受S-N 曲线的影响较大。如果S-N 曲线与真实试验数据的偏差较大，那么扩充数据与真实试验数据之间会有较大偏差；如果S-N 曲线与真实试验数据越接近，那么扩充数据与真实试验数据之间的偏差越小。

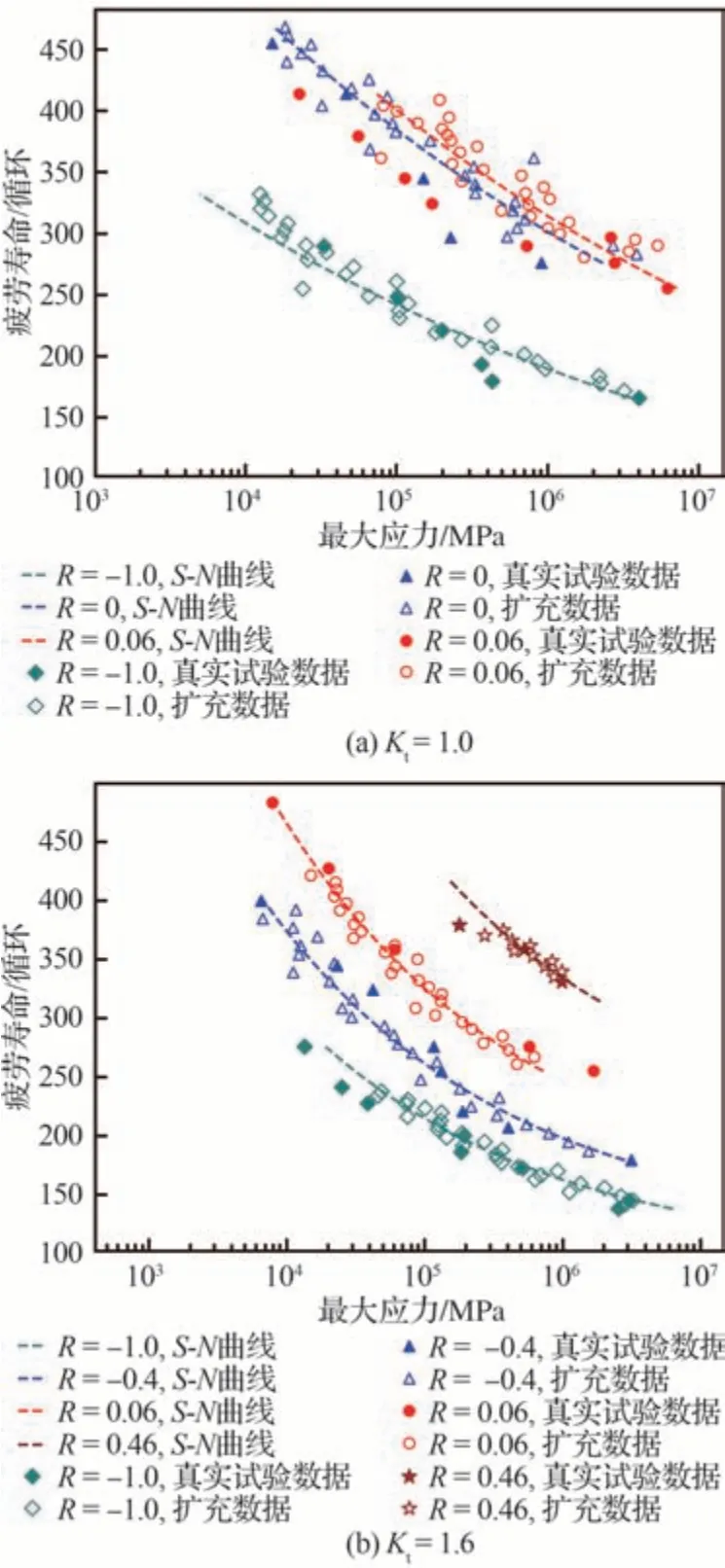
图13 扩充数据、试验数据及S-N 曲线的对比Fig.13 Comparison of extended data，experimental data，and S-N curve

接着，采用损伤力学数值方法计算相应工况下的寿命及预测误差。最后，将不同应力集中系数、不同应力比和不同应力水平下的数值方法预测误差整合成机器学习过程所需的模型数据库。按照70%、15%、15%的比例将模型数据库划分为训练集、验证集和测试集。这里，选择训练集数据的原则是使训练集数据能够具有代表性、多样性以及各个类型数据的平衡性。针对机器学习预测模型，一般而言，当总数据集的数据量小于1 万时，当训练集所占的比例为70%时，预测结果可以满足精度要求。本文在数据选取过程中，首先将所有不同应力集中系数、不同应力比、不同应力水平的200 组数据进行多次随机混合，然后从混合均匀的数据集中选取前70%作为训练集数据。

对于SVM 模型的疲劳寿命预测结果，常用的评价指标为均方误差（Mean Squared Error，MSE）和决定系数（R-Squared，R2）。MSE 反映了预测值与真实值之间差距的平方的平均值。MSE 的值越小，说明模型对数据的拟合程度越好。然而，MSE 对异常值的敏感度较高，因为它会对误差进行平方处理，从而放大异常值的影响。R2度量回归模型解释数据变异性的程度。R2的取值范围为0～1 之间，最佳值为1，表明模型完全解释了数据的变异性。当R2值较小时，模型未能很好地解释数据的变异性。R2的优势在于它具有可解释性，可用于比较不同模型的R2值以选择最佳模型。R2和MSE 的计算公式为

式中：yi表示第i个观测值的真实值表示模型对第i 个观测值的预测值表示所有预测值的平均值，n 表示样本数量。

3.3 结果与讨论

3.3.1 疲劳寿命预测结果

针对不同的应力集中系数、应力比和应力水平，采用损伤力学有限元数值计算方法，得到了200 组2014-T6 铝合金的疲劳寿命与试验疲劳寿命的误差。将数据划分为3 部分：140 组作为训练集，27 组作为验证集，33 组作为测试集。对支持向量机（SVM）模型起主要影响的参数包括惩罚参数C、径向基核函数（RBF）的相似度参数γ和容忍度参数ε。在训练过程中，采用粒子群优化方法结合验证集进行迭代交叉验证，以获得最优模型参数。模型参数和整体预测性能评价指标如表6 所示。训练集、验证集、测试集以及整体数据的线性回归图如图14 所示。观察可知，所有数据集的回归相关系数Rc均在0.8 左右，表明SVM模型具有较好的预测性能。

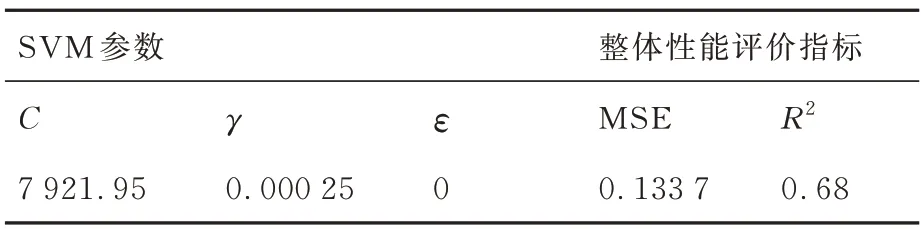
表6 SVM 模型参数及性能评价指标Table 6 SVM model parameters and performance evaluation indicators

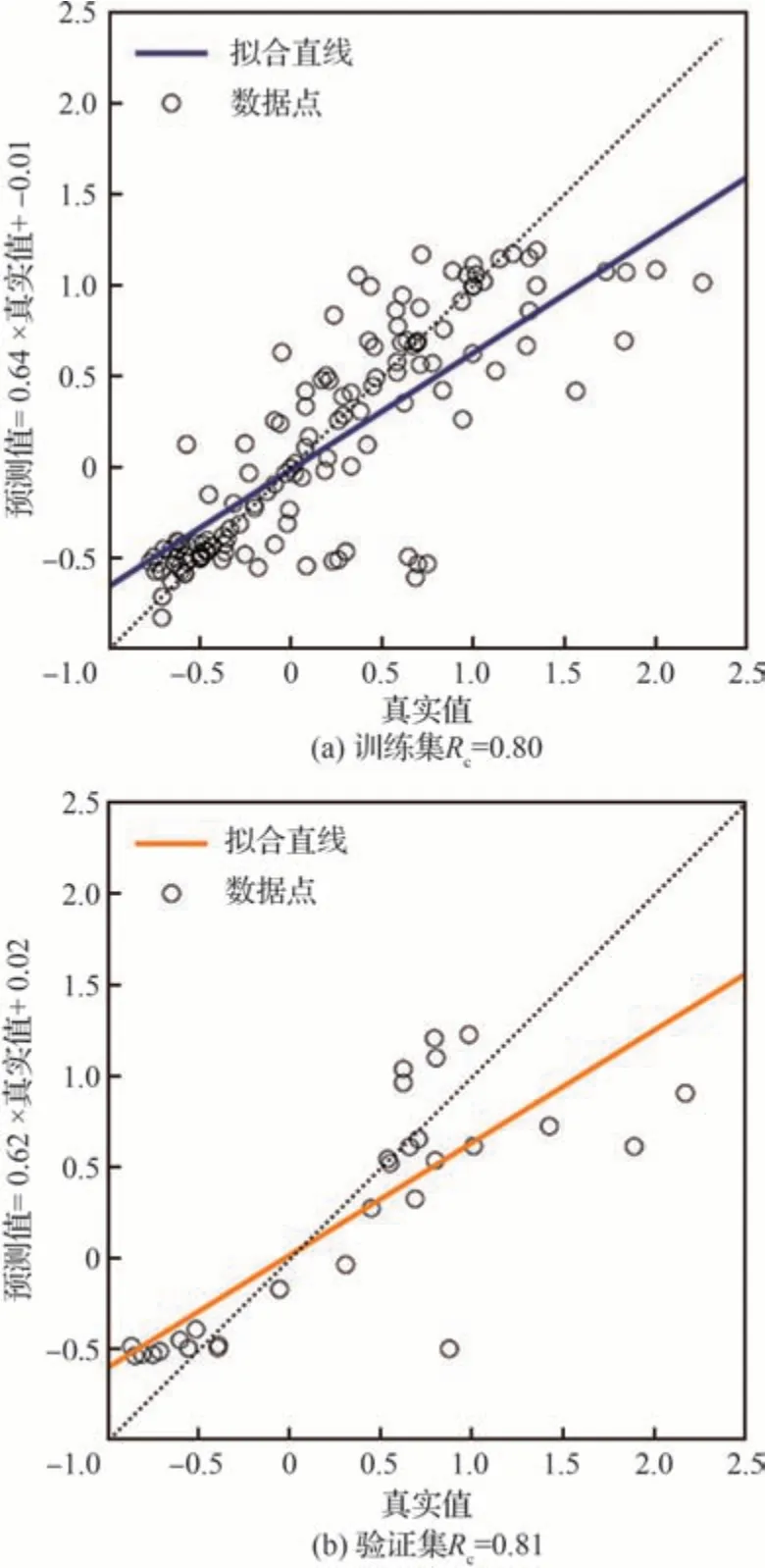
图14 SVM 模型预测结果线性回归图Fig.14 Linear regression graphs of SVM model prediction results

利用训练完成的SVM 模型对损伤力学数值方法计算的疲劳寿命误差进行预测，从而修正有限元数值计算结果。图15 展示了训练集修正后的结果与试验结果的对比，误差柱状图如图16 所示，其中，FEM model 指基于损伤力学的有限元数值方法，FEM-SVM model 表示结合SVM 模型进行修正的有限元数值方法。结果表明，对于Kt=1.0和Kt=1.6 时的数值计算结果，在经过SVM 模型修正后，3 倍误差带以外的数据点均进入了3 倍误差带内，整体数据明显向2 倍误差带内部及直线y=x 靠拢，寿命预测精度得到了显著提高。如图16 所示的误差柱状图表明，除个别数据点外，预测误差大幅降低，表明寿命SVM 修正方法显著提高了预测结果的准确性。

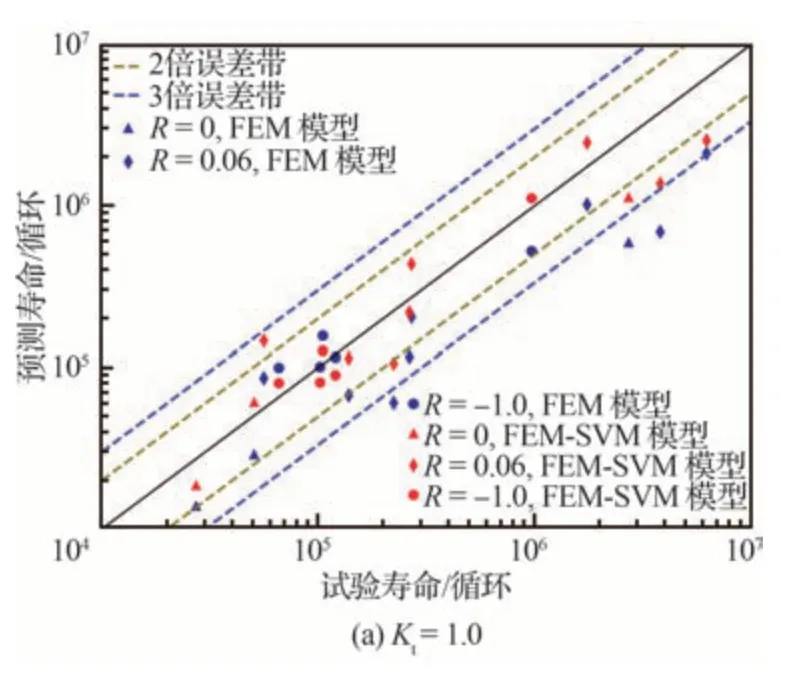
图15 修正前后试验寿命与预测寿命对比Fig.15 Comparison of experimental life before and after correction with predicted life

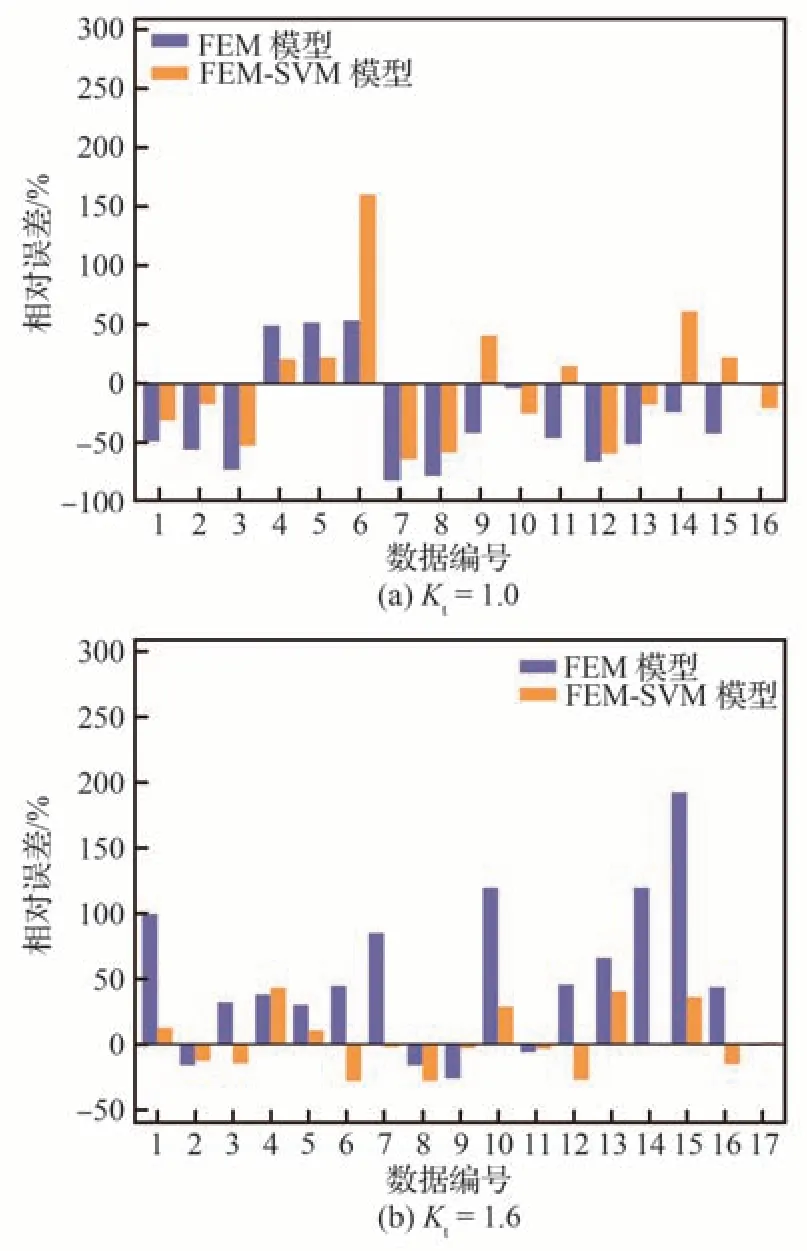
图16 修正前后寿命预测误差对比Fig.16 Comparison of prediction error before and after correction

3.3.2 应力水平及应力集中系数对损伤演化的影响

1）最大应力及应力比影响分析

应力集中系数Kt=1.0 应力比R=0.06时，σmax分别为400 MPa、350 MPa和300 MPa下损伤度随循环次数的变化曲线如图17（a）所示。最大应力σmax=290 MPa时，应力比分别为R=-0.4、R=0、R=0.1 下损伤度随循环次数的变化曲线，如图17（b）所示。结果表明，在应力比相同时，随着应力水平的升高，损伤演化速率明显加快，导致2014-T6 的疲劳寿命大幅降低。此外，在应力水平保持一致的情况下，应力比的减小同样会导致损伤演化速率迅速增长，从而使疲劳寿命显著下降。上述结果从损伤力学的角度揭示了应力水平和应力比对损伤演化和疲劳寿命的影响规律。

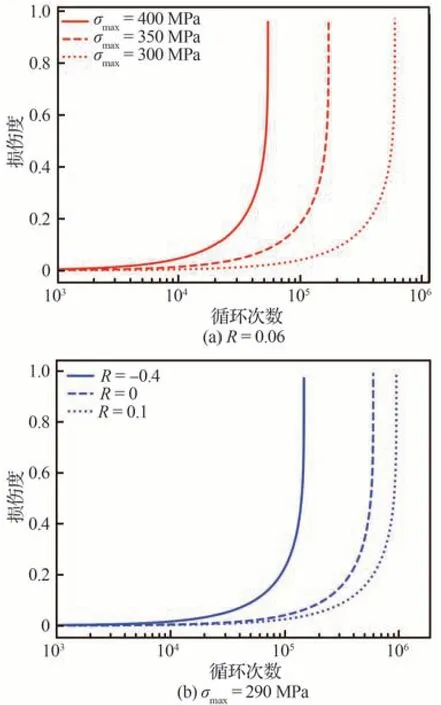
图17 不同应力水平下损伤度随循环次数变化曲线和不同应力比下损伤度随循环次数变化曲线Fig.17 Damage variable vs number of cycles curve under different stress levels and damage variable vs number of cycles curve under different stress ratios

2）应力集中系数影响分析

在应力比R=-1，最大应力σmax=160 MPa时，计算了应力集中系数Kt为1.6、2.0、2.4、3.4的含缺口2014-T6 试样危险点的损伤度及损伤速率随循环次数的变化规律，如图18、图19 所示，可以看到，在相同的载荷水平下，损伤演化速率随应力集中系数的增大而迅速加快，不同应力集中系数下的损伤演化速率具有很大差异，表明试件的形状尺寸对其疲劳性能有着至关重要的影响。

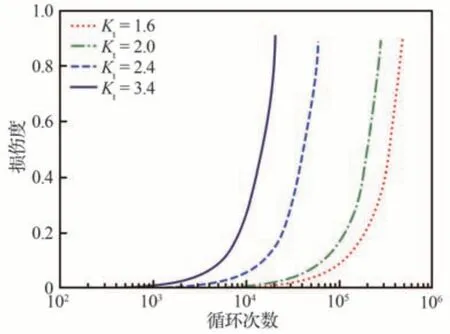
图18 不同应力集中系数下损伤度随循环次数变化曲线Fig.18 Damage variable curves with respect to cycle numbers under different stress concentration factors

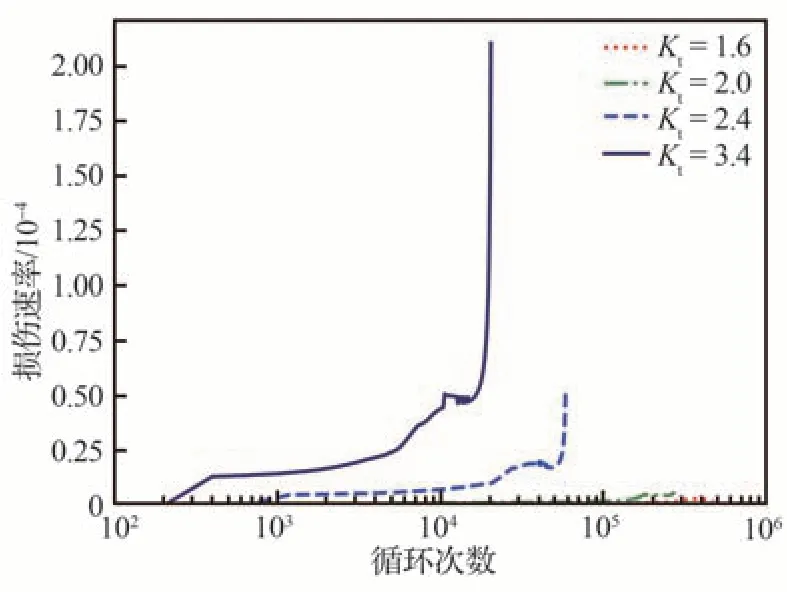
图19 不同应力集中系数下损伤速率随循环次数变化曲线Fig.19 Damage rate curves with respect to cycle numbers under different stress concentration factors

3.3.3 训练数据量及参数对SVM 模型预测性能的影响

1）训练数据量的影响分析

将3.3.1 节中的总体数据划分为训练集和测试集2 部分，保持模型参数不变。选取40 组数据作为固定测试集，然后从剩余数据中分别抽取40组、80 组、120 组、160 组作为 训练集数据，对SVM 模型进行训练并对测试集数据进行预测。图20 展示了不同训练数据量下测试集的线性回归图，观察可知，随着训练数据量的增加，预测值与真实值的线性相关度逐步提升。图21 展示了整体性能评价指标MSE和R2随训练数据量的变化以及SVM 模型在单个数据点的预测精度的变化。结果表明，MSE 随着训练数据量的增加而减小，R2随着训练数据量的增加而增大。同时，两者的变化速率逐渐降低。此外，随着训练数据量的增加，测试集中单个数据点预测值与真实值之间的差距逐渐减小。图22 对比了不同训练数据量下的预测寿命与试验寿命，可见，随着训练数据量的增加，数据点逐渐向y=x 直线靠拢。结果表明，训练数据量的增加对SVM 模型的预测性能有显著提升作用。然而，当数据量增大到一定程度时，预测性能的提升速度减缓并趋于收敛。这意味着，在实际应用中，需要权衡数据量与预测性能之间的关系，以寻找合适的训练数据量。

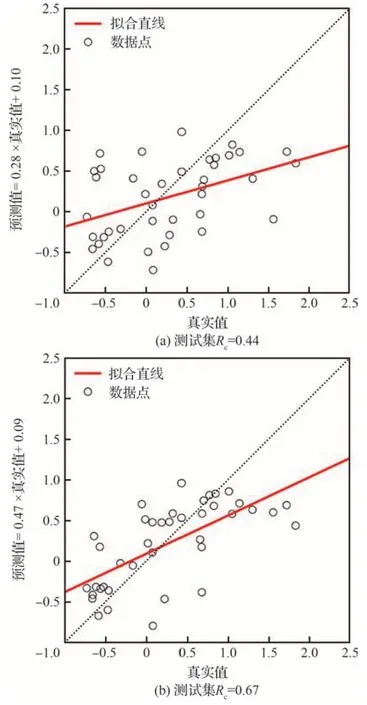
图20 不同训练数据量下测试集线性回归图Fig.20 Linear regression graphs of test set with varying training data sizes

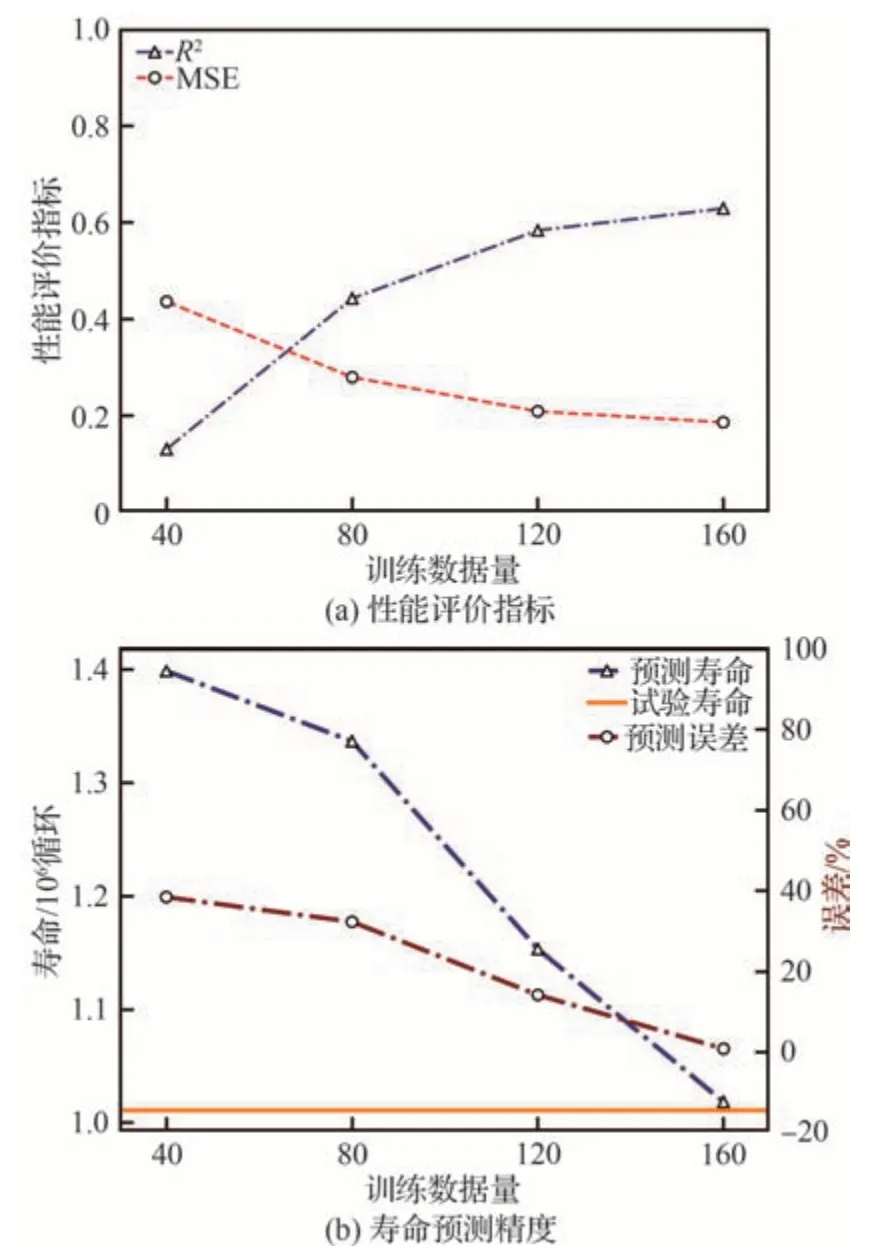
图21 模型预测性能随训练数据量变化规律Fig.21 Variation of model prediction performance with sizes of training data

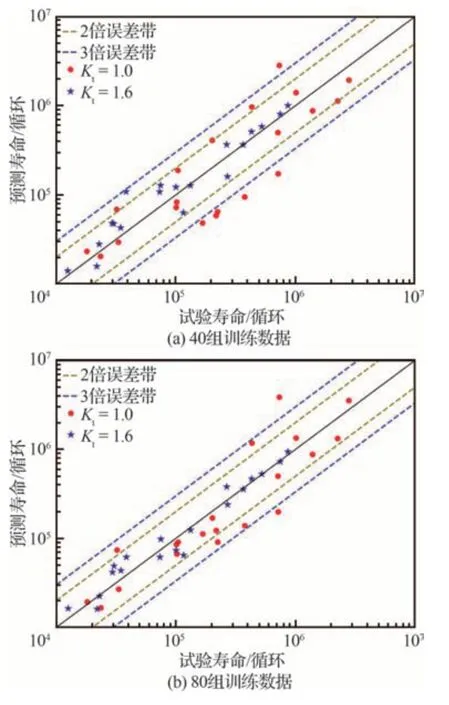
图22 不同训练数据量下预测寿命与试验寿命对比Fig.22 Comparison of predicted life and experimental life with varying training data sizes

2）参数C和γ 的影响分析

将3.3.1 节中的总体数据划分为训练集和测试集2 部分，其中训练集包含160 组数据，测试集包含40 组数据。首先，选取不同的参数C 进行训练，然后，对测试集进行预测。图23 展示了SVM模型整体性能评价指标及其在单个数据点的预测精度随参数C 的变化曲线。观察可知，当参数C 较小时，MSE 随着C 的增加迅速减小，而R2则快速增大。当C 增大到约7 921.95 附近时，预测性能的提升趋于稳定。同时，在选取的单个数据点上，模型预测精度呈现出先增大、后减小、再增大的变化趋势。接下来，选取不同的参数γ 进行训练，并对测试集进行预测。图24 展示了SVM模型整体性能评价指标及其在单个数据点的预测精度随参数γ 的变化曲线。结果表明，当γ 增大到最优参数0.000 25 之前，MSE 随着γ 的增加迅速减小，而R2则快速增大，表明模型预测性能得到了快速提升。然而，当γ 超过最优参数后，MSE 随着γ 的增加反而迅速增大，R2则快速减小，表明模型预测性能出现了快速下降。在选取的单个数据点上，模型的预测精度随着γ 的增加先呈现出增大、后减小的变化趋势。上述结果表明，在SVM 模型中，参数C和γ 对模型预测性能具有显著影响。因此，在实际应用中，需要通过合适的参数调整方法寻找最优参数组合，以实现最佳的预测性能。

图23 模型预测性能随参数C 变化规律Fig.23 Model prediction performance with variation in parameter C

图24 模型预测性能随参数γ 变化规律Fig.24 Model prediction performance with variation in parameter γ

4 结论

本文基于损伤力学理论与SVM 模型，针对2014-T6 铝合金材料，建立了一种疲劳寿命预测的新方法。主要结论如下：

1）基于连续损伤力学模型及UMAT 子程序的二次开发，建立了一种用于预测2014-T6 铝合金疲劳寿命的损伤力学有限元数值实现方法，并提出了基于粒子群算法的材料参数的标定方法。

2）利用支持向量机（SVM）模型对基于损伤力学的疲劳寿命预测结果的误差进行训练，从而修正数值预测结果，使得疲劳寿命预测准确性得到显著提高。

3）训练数据量、参数C和γ 对SVM 模型的预测性能有显著影响。在训练数据量逐步增加的过程中，SVM 模型预测性能得到明显提升，但当数据量增大到一定程度时，预测性能提升速度减慢并趋于收敛。在实际应用中，需要选取合适的模型数据库以及模型参数，以实现最佳预测效果。