机场安检排队系统资源优化配置

史跃亚, 张美蕙, 孙 唯

(1.中国民用航空飞行学院四川省民航机场智慧运营与运维工程研究中心, 四川 广汉 618307;2.中国民用航空飞行学院机场学院, 四川 广汉 618307; 3.三亚凤凰国际机场, 海南 三亚 572000)

机场安检服务作为最重要的地面保障服务之一,为了满足旅客服务需求、降低机场运行成本并保障安检服务的效率,有必要合理配置机场地面服务资源,从而减少离港旅客的安检服务等待时间、提高旅客服务的满意度并降低机场的运行成本。国外对排队服务问题的研究发展较早,研究范围和研究角度较为全面。Lindley[1]将GI/G/1排队模型应用于医疗领域,提出患者可以大大减少排队时间,改善医院排队时间长的问题;Denton和Gupta[2]提出建立线性动态调度模型,对预约时间间隔问题进行改进和优化,为合理的队列规划提供良好的参考价值和建议;Davis和Vollmann[3]通过大量调研,创建了旅客满意度和等候时间模型,发现游客排队等候的时间在不同时间段也存在差异,并提出了相关建议,有效改善了不同时间段的排队管理。国内学者对排队问题也颇有研究,尽管相对于西方国家起步较晚,但已经取得了一定的成果。曲禹达[4]在现有“通办”排队模型的基础上,选择单队列多业务通道的M/M/C队列模式,将多个业务通道作为集中队列区域;李嘉兴和李军[5]建立基于M/M/1排队模型的高低定价策略,优化系统性能;刘仁彬等[6]提出并建立了一种由策略N和D控制的M/G/1排队系统,在该策略下可以最小化系统的稳态成本。

目前关于资源优化配置的研究中,Roberta和Enrico[7]、Soemon和Tomoki[8]等使用0～1规划来建立整数规划模型,对安检柜台分配问题进行深入分析,充分利用现有资源,通过最优化柜台分配方案来提高旅客的服务体验;Nico和Erik[9]采用整数规划模型和流程仿真建模,建立数学模型,计算安检区服务率满足给定旅客服务满意度的各时间段内安检柜台的最小数量;Adrian和Sheldon[10]提出了一种新的多层次安检系统模型,通过对服务费和旅客到达排队系统的分析,优化安检系统的结构,并尝试利用新的安检模式来提高安检站的效率,保证机场的安全价值和成本;田超[11]利用派尔的实验性值机台规划系统,提出机场资源的有效配置可以满足不同旅客的多样化需求,同时降低航空公司和机场的日常运营成本,提高值机效率;杨扬[12]主要研究了离境旅客在办理乘机手续过程中排队聚集的现象,进而针对多个航班的离境办理登机手续创建了相应的排队模型,提出了人工值机柜台的动态分配策略;杨媛元等[13]提出了虚拟队列概念,将高峰乘客安全需求转移到空闲时段,并在不增加安全成本的情况下重新分配资源;史跃亚等[14]以博弈模型为理论基础,在机场安检区现有资源的基础上,进行疏散仿真优化,更好地保障了旅客人身安全。

本文以深圳宝安机场为例,根据安检排队系统现有资源进行优化配置。首先对目前安检排队系统进行介绍并发现安检排队系统中的瓶颈,针对瓶颈提出优化思想;然后基于资源优化配置的思想,建立双目标优化的资源优化配置模型,并根据NSGA-Ⅱ算法步骤使用Matlab进行模型解算,获得Pareto最优解集;最后运用TOPSIS方法,对Pareto最优解集进行排序,得出某一时段下,安检排队系统综合效益最优的配置方案。

1 相关理论

在目前的安检排队系统中,旅客在身份验证通道或自助验证闸机前面区域进行排队等待,等前一位旅客X光机安全检查和人身检查完成后才能进行下一步检查,这就可能导致旅客大量滞留在身份验证通道前并且对工作人员的利用效率也不高。为提高安检效率,对目前的安检排队系统进行优化布局设计,并对安检资源进行优化配置。进行优化布局设计后的机场安检排队系统,将身份验证归为Ⅰ级系统,将X光机安全检查和人身检查归为Ⅱ级系统,在Ⅰ级和Ⅱ级系统之间设计一个区域定义为缓冲系统,供旅客进行排队,旅客在完成身份验证后在此区域内可稍做停留进行Ⅱ级系统的窗口的选择[15]。优化布局后的安检排队系统如图1所示。

图1 安检排队系统优化模型

在对优化布局后的安检排队系统进行资源优化时,利用NSGA-Ⅱ算法,可以获得安检排队系统中通道资源动态配置问题的Pareto最优解集。然而,双目标优化问题的解不是唯一的,需要使用TOPSIS法的方法,从得出的Pareto解集中选择合适的解进行多目标资源优化决策。通常,决策者需要选择综合效益最好的方案进行具体配置,这一过程被称为后验评价。TOPSIS方法能够提供定量的评价结果,帮助决策者确定最适合的决策方案。通过该方法,决策者能够更加准确地评估和比较各个决策方案之间的优劣,并选择最佳的折中方案。

2 模型构建与算法设计

2.1 资源优化配置模型的构建

2.1.1 安检排队系统运营成本

为方便计算,假设安检区Ⅰ级系统内的每一个通道(每一组身份验证设备和所配备的工作人员为一个整体)的成本都为H1,Ⅱ级系统内的每一个通道(每一组安检设备和所配备的工作人员为一个整体)的成本都为H2,安检排队系统的运营成本公式为

minZ1=H1αi+H2βi

(1)

式中:Z1为安检排队系统总成本;αi为时段i下Ⅰ级系统开放的通道数;βi为时段i下Ⅱ级系统开放的通道数。

2.1.2 系统内旅客排队等待时间

(2)

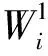
(3)

(4)

(5)

(6)

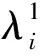
综上,在源优化配置过程中,将安检排队系统运营成本最优和旅客平均排队等待时间最小为目标建立安检资源配置模型如下:

minZ1=H1αi+H2βi

(7)

(8)

(9)

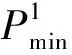
2.2 算法设计

对机场安检排队系统的运营成本和旅客等待时间设置了优化目标,并将多目标算法应用于动态配置过程中。多目标优化能够有针对性地研究不同成本目标,并展示优化目标之间的博弈关系,从而消除由于目标量纲不同而导致的优化结果置信度低的问题,NSGA-Ⅱ算法是目前解决多目标优化问题的常用算法之一,通过NSGA-Ⅱ算法可得到问题的Pareto最优解集[16]。换言之,通过多目标优化,能够更好地平衡安检排队系统的成本和旅客等待时间,确保系统的优化结果更具可靠性和准确性。NSGA-Ⅱ算法被应用于求解安检排队系统中通道资源动态配置模型,并在以下步骤中进行运行:

步骤1:编码。使用二进制编码方式对安检排队系统中通道的开放与关闭进行编码;

步骤2:设置安检排队系统资源动态配置问题的初始种群规模和其最大迭代次数,并随机生成初始种群;

步骤3:确定每个个体在两个优化目标函数值(安检排队系统中开放通道运营成本和旅客排队等待时间)上的非支配级别,并计算个体的拥挤距离;

步骤4:采用锦标赛机制选择两个个体进行交叉和变异计算,选择依据为快速非支配排序和拥挤距离的计算结果;

步骤5:进行精英保留策略;

步骤6:迭代次数加1,返回至步骤3,直到迭代次数达到设置的最大值为止。

通过上述步骤的迭代,NSGA-Ⅱ算法能够逐步优化安检排队系统中通道资源动态配置,寻找到安检排队系统中最优解的可能性最大化。这样能够提高安检系统的运行效率和旅客的体验。

TOPSIS方法实现步骤如下:①准备决策矩阵;②对决策矩阵进行归一化处理;③根据熵权法确定权重;④根据加权判断矩阵获得各决策目标的正负理想解;⑤计算各决策目标值与理想值之间的距离;⑥计算各决策目标的相对贴近度;⑦基于相对贴近度对各决策目标进行排序,得到决策结果。

3 实例分析

3.1 数据获取

3.1.1 航班数据统计

调查数据为深圳宝安国际机场2023年3月1日至3月31日每日国内出港旅客数,随机抽取时段内一天,以每一小时为单位,对06:00—23:59内的航班数和离港乘客数统计如表1所示。

表1 该机场全天国内航班统计数据

3.1.2 最大排队等待时间

3.2 NSGA-Ⅱ算法参数设置

仿真过程中随机选取表1中08:00—08:59时间段内机场安检排队系统内的相关数据进行解算,其中,表2给出了资源动态配置问题的原始数据,表3给出了算法的参数。

表2 机场安检排队系统动态配置原始数据

表3 设定算法参数

3.3 结果分析

基于安检排队系统资源优化配置模型运行NSGA-Ⅱ算法,使用Matlab进行求解,得到Pareto最优解,如表4所示。

表4 安检排队系统资源动态优化配置Pareto最优解

由表4可知,Ⅰ级系统和Ⅱ级系统开放通道数越多,安检排队系统运营成本越高,而在这个过程中,旅客排队等待的时间是逐步减少的,而在安检排队系统资源优化配置模型中,两个目标间均为越小越优,不想存在某一方案使优化的两目标值同时达到最小,由此可见,两目标之间存在博弈。

3.4 后验评价

TOPSIS法的决策过程可以从不同解集中寻找综合效益最优的解,步骤如下。

(1)评价指标同趋势化。在进行评价时,应使用所有指标变化方向一致,通常将低优指标和中指标全转化为高优指标,同趋势化的初始判断矩阵值如表5所示。

表5 同趋势化的初始判断矩阵值

(2)初始判断矩阵归一化。归一化处理后的矩阵值如表6所示。

表6 归一化矩阵值

(3)运用熵权法确定指标权重,如表7所示。

表7 指标权重计算

(4)计算各决策目标的正负理想解,如表8所示。

表8 正负理想解

(5)选择最终决策方案。计算各方案两目标值正负理想距离和各方案与最优方案的相对贴近度,并按相对贴近度进行排序,从而选出综合效益最优的配置方案,相对贴近度及排序结果如表9所示。

表9 不同优化配置方案排序结果

排序结果表明,Ⅰ级系统通道开放数为17个,Ⅱ级系统通道开放数为35个时的综合效益最好。

4 结语

在对安检排队系统进行资源优化配置的研究过程中,首先提出建立安检排队系统优化模型,优化后的安检排队系统分为Ⅰ级系统、Ⅱ级系统和缓冲系统三部分,在此基础上,建立双目标的安检排队系统资源优化配置模型,运用NSGA-Ⅱ算法进行解算,并使用TOPSIS方法进行后验评价,最终得出综合效益最优的配置方案。然而在研究安检排队系统资源优化配置的过程中,只建立了数学模型进行解算并得出结果,而实际情况下,旅客在进行安检的整个流程中,对队列的选择是基于自己意向的一个动态选择的过程。但过建立数学模型来描述旅客的整个安检过程时,只能根据情况人为的设定某一环节的参数数据,并不能将整个流程动态地展现出来,这就容易导致根据数学模型得出的结果比实际情况更加理想化。为了使结果更加真实,在之后的研究中可以进行仿真建模,对安检排队系统资源优化配置进一步的研究和验证。