应用滑动轴承的风电齿轮箱行星轮系动力学建模及解耦方法
唐浩 谭建军 李浩 朱才朝 叶伟 孙章栋
摘要:
在行星輪系动力学建模中,常以非线性油膜力或线性刚度阻尼形式考虑其对系统动力学特性的影响,前者仿真精度高但计算成本也高,后者计算效率高却忽略了油膜力和轴颈轴套偏心量的时变性,仿真精度有限。为此,以2MW级风电齿轮箱为研究对象,建立滑动轴承时变线性刚度阻尼模型,提出计入轴颈轴套时变偏心量的滑动轴承附加偏心修正力计算方法;利用行星架销轴行星轮变形协调关系,将时变线性刚度阻尼模型与附加偏心修正力进行耦合;建立应用滑动轴承的风电齿轮箱行星轮系动力学模型,对比了工况和轴承参数对模型计算精度与系统动态响应的影响,并通过试验加以验证。研究结果表明,齿轮副动态啮合力波动会使滑动轴承刚度阻尼系数和附加偏心修正力产生周期性变化;在稳定和瞬态工况下,提出的模型可以很好地预测系统响应,尤其是行星轮振动响应;减小滑动轴承宽径比与间隙、增大输入转矩可以改善系统均载性能。
关键词:风电齿轮箱;行星轮系;滑动轴承;动力学
中图分类号:TG315
DOI:10.3969/j.issn.1004132X.2024.04.003
开放科学(资源服务)标识码(OSID):
Research on Dynamic Modeling and Decoupling Methods of Planetary
Gear Trains in Wind Turbine Gearboxes with Journal Bearings
TANG Hao1 TAN Jianjun1 LI Hao1 ZHU Caichao1 YE Wei2 SUN Zhangdong3
1.State Key Laboratory of Mechanical Transmission for Advanced Equipment,Chongqing
University,Chongqing,400044
2.Chongqing Wangjiang Industry Co.,Ltd.,Jiangsu Branch,Yancheng,Jiangsu,224100
3.School of Mechanical Engineering,Hubei University of Automotive Technology,Shiyan,Hubei,442002
Abstract: In the dynamic modeling of planetary gear trains, the influences of nonlinear oil film forces or linear stiffness damping forms on system dynamics characteristics were often considered. The former had high simulation accuracy but high computational costs, and the latter had high computational efficiency but ignores the time-varying effects of oil film forces and journal sleeve eccentricity, resulting in limited simulation accuracy. Therefore, a 2MW wind turbine gearbox was taken as the research object herein. A time-varying linear stiffness damping model of the journal bearing was established, and a calculation method for the additional eccentricity correction force of the journal bearing considering the time-varying eccentricity of the journal sleeve was proposed. Then, the time-varying linear stiffness damping model was coupled with the additional eccentricity correction force by using the coordination relationship between the carrier-pin and planet. Finally, a dynamic model of the planetary gear trains in wind turbine gearboxes using journal bearings was established, and the effects of operating conditions and bearing parameters on the calculation accuracy and dynamic system responses were compared and verified through experiments. The results indicate that the fluctuation of dynamic meshing force in gear pairs may cause periodic changes in the stiffness damping coefficient and additional eccentricity correction force of journal bearings. The proposed model may effectively predict system responses, especially planetary gear vibration responses, under stable and transient operating conditions. Reducing the width-diameter ratio and gap, increasing input torque may improve the system's load sharing performance.
Key words: wind turbine gearbox; planetary gear train; journal bearing; dynamics
收稿日期:20231214
基金项目:国家重点研发计划(2022YFB4201100);重庆市技术创新与应用发展专项重点项目(CSTB2022TIAD-KPX0051);国家海上风力发电工程技术研究中心开放基金(HSFD22005)
0 引言
行星轮系具有功率密度高、结构紧凑等优点,被广泛应用于风电齿轮箱中。在行星轮系中,行星轮常采用滚动轴承进行支撑,但随着风电齿轮箱功率的不断增大,高载荷下低成本与高功率密度设计之间的矛盾日益凸显。为此,部分风电齿轮箱企业陆续开始将成本低、结构简单可靠的滑动轴承应用于行星轮,实现“以滑代滚”,但这种改变会将常规的预紧滚动轴承“负游隙”支撑转变为滑动轴承“正游隙”支撑,造成行星轮系动力学特性复杂。同时,滑动轴承油膜润滑计算步长短、迭代频繁且收敛困难,而复杂风电工况下系统响应稳定时间长,造成两者耦合建模难度大,计算成本高。因此,开展应用滑动轴承的风电齿轮箱行星轮系动力学建模及解耦方法研究具有重要意义。
目前,国内外学者围绕滑动轴承转子系统动力学开展了大量研究。LUND等[1]首次推导了滑动轴承支撑刚度阻尼系数,此外,LUND[2-3]还提出了通过频率相关分析计算滑动轴承支撑刚度与阻尼系数的方法。基于该理论,MAJUMDAR等[4]采用一阶时变摄动法计算了滑动轴承线性支撑刚度阻尼系数,并将其应用于水润滑轴承分析。类似地,YANG等[5-6]利用时变摄动法分析了气动滑动轴承线性支撑刚度阻尼系数。HUSSEIN等[7]利用时变二阶摄动法得到了滑动轴承线性和非线性支撑刚度阻尼系数,建立了双对称滑动轴承柔性转子动力学模型。TAMER等[8]则采用三阶非线性轴承支撑刚度阻尼系数计算轴承力,研究了滑动轴承支撑下柔性Jeffcott转子系统的稳定性和分岔问题。此外,不少学者采取多种简化油膜力模型分析滑动轴承转子系统动力学特性,例如,YANG等[9]基于有限差分法,通过求解具有轴承波纹度的雷诺方程,建立了非线性油膜力支撑的转子系统动力学模型;CHANDAN等[10]建立了滑动轴承刚性转子系统动力学模型,其中采用无限长轴承模型计算滑动轴承响应;DAKEL等[11]采用Timoshenko梁单元构建了具有滑动轴承支撑的船载转子动力学模型,并通过求解雷诺方程计算了滑动轴承油膜反力。
滑动轴承还被广泛应用于齿轮传动系统中,保障多级传动系统实现增速或减速传动。基于滑动轴承等效刚度阻尼系数计算理论,学者们开展了大量研究,ZHANG等[12]研究了考虑销轴误差的滑动轴承对行星轮系均载特性的影响;随后,ZHANG等[13]进一步考虑推力滑动轴承的影响,并考虑时变啮合刚度、传动误差和齿侧间隙等对径向滑动轴承和推力滑动轴承的刚度阻尼系数方程进行了建模;YANG等[14]考虑行星轮滑动轴承偏心量与轴承支撑刚度阻尼的不对称性和相互作用,建立了应用滑动轴承的人字形行星轮系耦合动力学模型;YIN等[15]、YANG等[16]采用刚度阻尼系数描述行星轮滑动轴承支撑的不对称性和相互作用,建立了齿轮系统动力学模型。也有一些学者采用有限元分析方法,如HAGEMANN等[17-18]基于热弹流体动力学,研究了结构变形对风电齿轮箱行星轮系行星滑动轴承的影响。
综上可知,在传动系统动力学建模过程中,滑动轴承建模方法主要包括有限元法与解析法两大类。有限元法主要通过提取滑动轴承载荷、运动等边界条件,采用有限元仿真软件建立滑动轴承局部传动系统结构有限元模型。该方法可以实现滑动轴承流固热多场耦合精细化仿真,但常采用静态边界条件,难以应用于动态场景。解析法可以考虑滑动轴承动态边界条件,通过对雷诺方程直接积分获取滑动轴承瞬态压力分布,或通过扰动雷诺方程得到滑动轴承等效线性刚度阻尼系数。前者计算成本高但精度较高,后者虽然计算效率高但忽略了刚度阻尼时变性,计算精度有限。目前针对采用刚度阻尼形式的滑动轴承建模改进方法的相关研究鲜有报道。
本文以2MW级风电齿轮箱为研究对象,建立滑动轴承时变线性刚度阻尼模型;推导考虑轴颈轴套时变偏心量的滑动轴承附加偏心修正力方程;利用行星架销轴行星轮变形协调关系,将时变线性刚度阻尼模型与附加偏心修正力进行耦合,建立应用滑动轴承的风电齿轮箱行星轮系动力学模型;最后,分析工况和轴承参数对模型计算精度与系统动态响应的影响,并开展试验验证。
1 风电齿轮箱传动原理
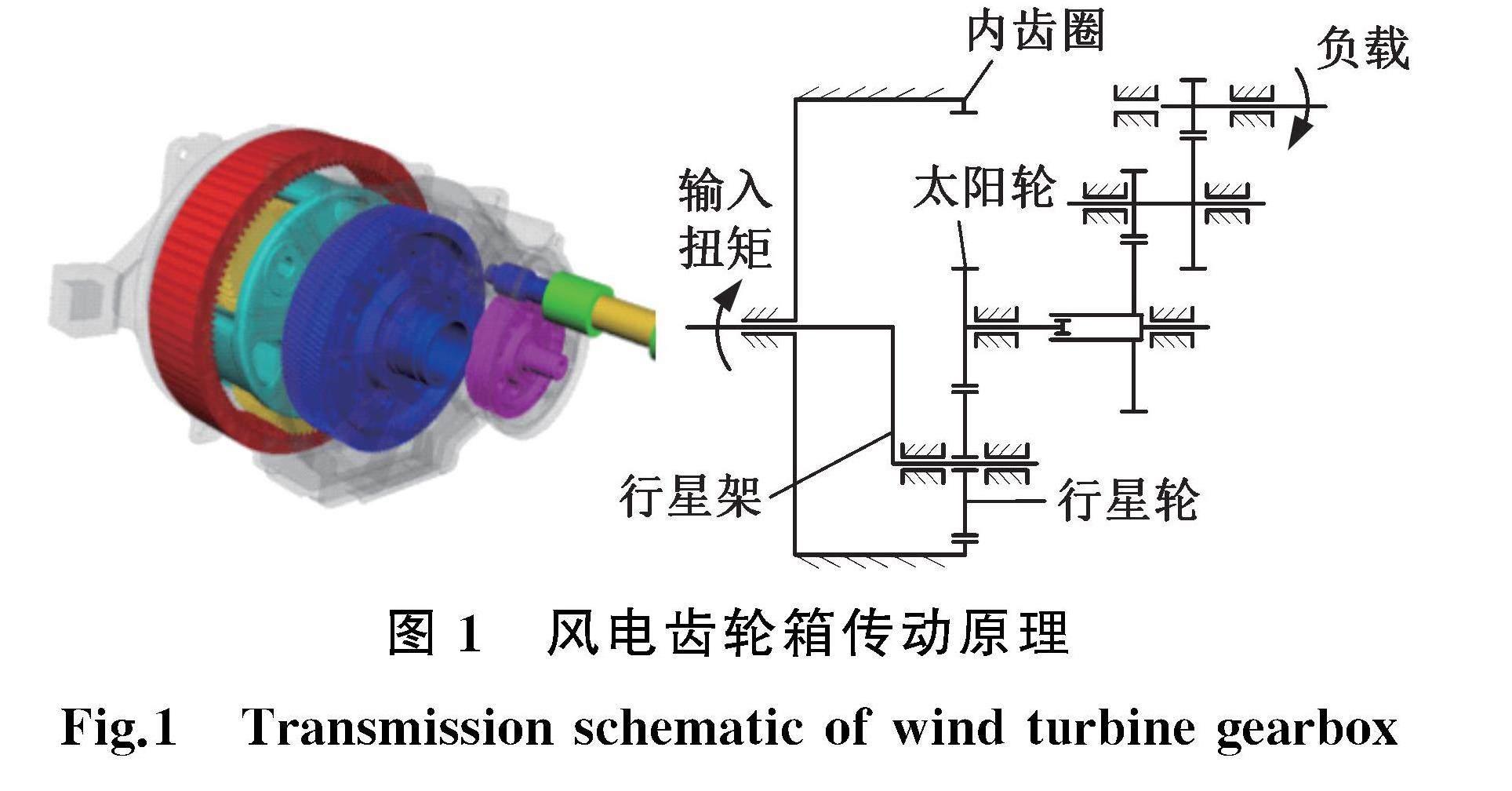
图1所示为2MW级风电齿轮箱传动结构,主要由一级行星轮系和两级定轴轮系组成。在行星轮系中,行星轮内孔作为滑动轴承轴套,行星架销轴作为滑动轴承轴颈,两者通过相对运动形成油膜,实现对行星轮的支撑。图2所示为行星轮滑动轴承在行星轮系的布置位置。表1、表2所示分别为行星轮系与行星轮滑动轴承的基本设计参数。
2 滑動轴承建模
2.1 非线性油膜力——模型Ⅰ
一般地,流体二维雷诺方程可表示为[19]
x(ρh3μpx)+y(ρh3μpy)=6(U2-U1)(ρh)x+
6ρh(U1+U2)+12ρ(n2-n1)(1)
式中,h为油膜厚度;p为油膜压力;μ为流体黏度;ρ为流体密度;U1为轴瓦周向转速;U2为轴颈周向转速;n1为轴瓦径向转速;n2为轴颈径向转速;x、y为销轴相对行星轮内孔的位置。
式(1)等号右边依次为楔形项、伸张项及挤压膜项,分别表示楔形间隙、切向速度变化和表面的法向接近对油膜压力的影响。由于ρ是常数,且在稳态下可省略伸张项,因此可将式(1)简化为
x(h3μpx)+y(h3μpy)=6Uhx+12ρn(2)
对式(2)作量纲一处理,令φ=2x/D,λ=2y/L,H=h/c(c为滑动轴承间隙),得到滑动轴承量纲一雷诺方程:
φ(H3pφ)+(DL)2λ(H3pλ)=Hφ+2Ht(3)
Hφ=1-xsin φ-ycos φ
Ht=-x·sin φ-y·cos φ
式中,H为量纲一后的油膜厚度;λ为量纲一轴承宽度;D为滑动轴承直径;L为滑动轴承宽度;φ为节点位置角;x·、y·为销轴相对行星轮内孔的位置。
根据式(3),直接采用有限差分法求解油膜压力p[20]。对油膜压力p沿宽度与圆周方向同时积分,可得油膜力计算公式为
Fx=-∫1-1∫2π0psin φdφdλ
Fy=-∫1-1∫2π0pcos φdφdλ(4)
如图3所示,将式(4)分别沿宽度与圆周方向进行离散化处理并求和,可得
Fx=∑nk=1Fxk
Fy=∑nk=1Fyk(5)
式中,Fxk、Fyk分别为第k个圆周离散节点油膜压力沿宽度方向的合力在自身参考坐标系xpi轴和ypi轴上的投影。
solve oil film force
2.2 线性刚度阻尼——模型Ⅱ
基于式(3),采用压力扰动法对油膜力(Fx、Fy)、油膜压力(p)及油膜厚度(h)作如下展开[21]:
Fx=Fx0+kxxΔx+kxyΔy+cxxΔx·+cxyΔy·
Fy=Fy0+kyxΔx+kyyΔy+cyxΔx·+cyyΔy·
p=p0+pxΔx+pyΔy+px·Δx·+py·Δy·
h=h0+Δxsin φ+Δycos φ
(6)
式中,Fx0、Fy0为稳态下油膜力;p0为稳态下油膜压力;h0为稳态下油膜厚度;Δx、Δy为当前时刻销轴相对行星轮内孔位置的小扰动量;kxx(cxx)、kyy(cyy)分别为沿xpi轴和ypi轴的等效刚度(阻尼);kxy(cxy)、kyx(cyx)为xpi轴与ypi轴之间的耦合刚度(阻尼);px、py分别为沿xpi轴与ypi轴的位移引发的扰动压力。
将式(6)代入式(3),可得4组扰动雷诺方程:
φ(H30pxφ)+(DL)2λ(H30pxλ)=cos φ-
3sin φH0H0φ-3H30p0φφ(sin φH0)
φ(H30pyφ)+(DL)2λ(H30pyλ)=cos φ-
3sin φH0H0φ-3H30p0φφ(sin φH0)
φ(H30px·φ)+(DL)2λ(H30px·λ)=2sin φ
φ(H30py·φ)+(DL)2λ(H30py·λ)=2cos φ(7)
最后,采用有限差分法求解得到4组线性刚度阻尼系数[21],分别如下:
kxx=-∫1-1∫2π0pxsin φdφdλ
kyx=-∫1-1∫2π0pxcos φdφdλ
kxy=-∫1-1∫2π0pysin φdφdλ
kyy=-∫1-1∫2π0pycos φdφdλ(8)
cxx=-∫1-1∫2π0px·sin φdφdλ
cyx=-∫1-1∫2π0px·cos φdφdλ
cxy=-∫1-1∫2π0py·sin φdφdλ
cyy=-∫1-1∫2π0py·cos φdφdλ(9)
如图4所示,根据式(8)和式(9),可得油膜力计算公式为
KX+CX·=F(10)
K=kxxkxykyxkyy
C=cxxcxycyxcyy
X=ΔxΔy X·=Δx·Δy· F=FxFy
2.3 刚度阻尼修正——模型Ⅲ
通过式(8)和式(9)可以计算当前载荷工况下滑动轴承等效线性刚度阻尼,但大多数模型是直接通过受力分析得到滑动轴承载荷边界,忽略了制造安装误差激励对滑动轴承载荷边界的动态影响。同时,式(8)和式(9)中的线性刚度阻尼仅适用于在穩态位置附近产生小扰动(Δx和Δy)的情况,难以体现稳态位置自身(x和y)的变化,故无法考虑销轴与行星轮内孔之间的偏心量。
如图5所示,基于式(10),建立考虑刚度阻尼时变性与附加偏心修正力的油膜力计算模型:
KvX+CvX·+fv=F(11)
式中,Kv、Cv分别为时变的刚度阻尼系数矩阵,与式(10)中的表达式一致;fv为附加偏心修正力矩阵。
to solve oil film force
2.3.1 时变的刚度阻尼系数
为了获取随载荷变化的时变刚度阻尼系数,若仅简单地根据输入载荷工况变化不断地重复计算式(8)和式(9),系统仿真耗时巨大。本文采用代理模型方法,预先建立滑动轴承作用载荷集{fb1,fb2,…,fbn}与对应的轴承刚度矩阵集{Kb1,Kb2,…,Kbn}、阻尼矩阵集{Cb1,Cb2,…,Cbn}之间的映射关系,具体构建过程如下:
(1)通过行星轮系受力分析,确定作用在行星轮滑动轴承上的载荷fb及其区间范围,本文选取的滑动轴承区间为[2,2000]kN;
(2)对滑动轴承区间进行等间隔划分,可得到滑动轴承作用载荷集{fb1,fb2,…,fbn},本文选取划分数量为2000;
(3)根据式(8)和式(9),批量计算载荷集中每个载荷所对应的刚度阻尼系数矩阵,建立轴承刚度矩阵集{Kb1,Kb2,…,Kbn}、阻尼矩阵集{Cb1,Cb2,…,Cbn};
(4)采用多项式拟合、支持向量机以及神经网络等代理模型方法,构建输入集与输出集之间的映射,并开展预测精度验证[22]。
若预测精度不满足要求,可以增大载荷集划分数量,并重复步骤(1)~步骤(4),直至满足精度要求,最终可获取随载荷变化的时变刚度系数矩阵Kv和阻尼系数矩阵Cv。本文采取多项式拟合方法构建输入集与输出集的映射。
2.3.2 附加偏心修正力
在行星轮系中,行星轮同时受到太阳轮啮合力Fspi、内齿圈啮合力Frpi以及销轴轴承支撑力F,但由于行星轮主要承受切向载荷,因此主要考虑切向载荷平衡,建立行星轮沿ypi轴方向的受力平衡方程:
Fy=(Fspicos γspi+Frpicos γrpi)cos β(12)
γspi=αsp+Φpi
γrpi=αrp-Φpi
Fspi=kspi(eDspi+eTspi)
Frpi=krpi(eDrpi+eTrpi)
式中,αsp为太阳轮行星轮端面啮合角;Φpi为行星轮位置相角;αrp为内齿圈行星轮端面啮合角;β为基圆螺旋角;kspi(krpi)为太阳轮(内齿圈)行星轮啮合刚度;eD为动态传动误差(与载荷相关);eT为静态传动误差(与误差相关)。
根据式(12)中各项系数是否与载荷、误差相关,可将其改写为
F=FxFy=0F0+ΔFxΔFy(13)
其中,F0为与载荷工况相关项,即
F0=(kspieTspicos γspi+krpieDrpicos γrpi)cos β≈TinNprc(14)
ΔF为与误差相关项,即
ΔFx=(kspieTspisin γspi-krpieTrpisin γrpi)cos β
ΔFy=(kspieTspicos γspi+krpieTrpicos γrpi)cos β(15)
式中,Tin为输入扭矩;Np为行星轮数量;rc为太阳轮行星轮中心距。
将式(12)代入式(11),同时借助压力扰动法思想,将式(11)中X(X·)在稳态位置处进行展开,可得
fv=0F0+ΔFxΔFy-Kv(X0+ΔX)-Cv(X·0+ΔX·)(16)
式(16)中,X0(X·0)为在载荷F0作用下的稳态位置(速度),并满足ΔFxΔFy=KvΔX+CvΔX·,X·0=0。因此,式(16)可简化为
fv=0F0-KvX0(17)
3 变形协调关系
3.1 齿轮副
如图6所示,在行星轮系中,太阳轮与内齿圈同时与N个行星轮产生啮合。定义太阳轮行星轮i、内齿圈行星轮i的广义位移向量为
Xζpi=(xζ,yζ,zζ,θxζ,θyζ,θzζ,xpi,ypi,zpi,θxpi,
θypi,θzpi)T(18)
式中,ζ=s,r,分别表示太阳轮与内齿圈。
将式(18)中的太阳轮、内齿圈和行星轮i的6个自由度位移分别沿太阳轮行星轮i、内齿圈行星轮i啮合线进行投影叠加,可得各自啮合副的啮合刚度矩阵:
Ksi=kspiVTsiVsi=kspssikspspiksppsikspppi(19)
Kri=krpiVTriVri=krprrikrprpikrpprikrpppi(20)
其中,Vsi、Vri分别为太阳轮行星轮i、内齿圈行星轮i的啮合矢量,具体参见文献[23]。啮合阻尼矩阵与啮合刚度矩阵类似,不再赘述。
齿轮在加工制造的过程中存在误差,会使齿轮的实际齿廓形貌和位置与理想存在偏移,引起齿轮啮合过程周期性的传动误差激励,可将齿形误差表示为与齿轮转动角位移相关的简谐函数[23]。
3.2 行星轮销轴
径向滑动轴承主要为行星轮提供径向支撑,为了抵消斜齿轮轴向力,常采用推力滑动轴承提供轴向支撑,但这不是本文分析重点,因此忽略两类滑动轴承之间的耦合作用,并将推力滑动轴承简化为线性刚度阻尼系数。
将模型Ⅰ、Ⅱ、Ⅲ计算的油膜力统一改写为Fjb,可建立行星轮6自由度受力平衡方程:
mpix¨pi=Fjb_pix+(-Fspisin αsp+Frpisin αrp)cos β
mpiy¨pi=Fjb_piy+(Fspicos αsp+Frpicos αrp)cos β
mpiz¨pi+czpiz·pi+kzpizpi=Fspisin β-Frpisin β
Ixpiθ¨xpi+cθxpiθ·xpi+kθxpiθxpi=0
Iypiθ¨ypi+cθypiθ·ypi+kθypiθypi=
Fspisin βcos αsp+Frpisin βcos αrp
Izpiθ¨zpi=-Fspicos β+Frpicos β(21)
式中,mpi為行星轮i的质量;Ixpi、Iypi、Izpi分别为绕xpi轴、ypi轴和zpi轴的转动惯量;kθxpi、kθypi分别为绕xpi轴和ypi轴的轴承支撑刚度,本文取值1×1011 N·m。
3.3 行星轮系动力学模型
根据太阳轮、内齿圈、行星架和行星轮节点自由度及其耦合关系,定义系统节点在自身参考坐标下的广义位移向量为
Xsys=(XTs,XTc,XTr,XTp1,…,XTpNp)T(22)
式中,Xs、Xc、Xr、Xp分别为太阳轮、行星架、内齿圈以及行星轮的广义位移向量。
根据式(22)中各节点编号,将各构件质量矩阵、刚度矩阵以及阻尼矩阵进行组装,可建立行星轮系动力学模型:
MsysX¨sys+CsysX·sys+KsysXsys=Fsys+Fjb(23)
式中,Msys为系统质量矩阵;Ksys为系统刚度矩阵;Csys为系统阻尼矩阵,Fsys为激振力矩阵;Fjb为滑动轴承油膜力矩阵。
式(23)中齿轮副啮合刚度计算参考标准DIN 3990—1987a[24],并考虑齿形误差影响[25]。
采用精细积分法[26]求解式(23),计算流程如图7所示。考虑到低速重载对模型Ⅰ求解精度的影响,在对模型Ⅰ、Ⅱ、Ⅲ求解时,时间步长统一设置为1×10-7 s,初始位移与速度初始值统一设置为1×10-4。
4 结果与分析
4.1 滑动轴承模型验证
为了验证滑动轴承线性刚度阻尼系数(模型Ⅱ)计算过程的正确性,选用文献[27]滑动轴承参
数(表3)作为模型Ⅱ输入,并将计算结果与文献[27]的结果进行对比,如表4所示。从表4中可知,计算的刚度阻尼系数最大误差仅6.48%,验证了结果的有效性。
4.2 稳态工况对比
稳态工况下行星轮系动态响应可以直接反映滑动轴承对系统动力学特性的长期影响规律。为此,在额定工况下(输入扭矩为1.543 MN·m,输入转速为13.68 r/min),对比了三种滑动轴承模型(模型Ⅰ、Ⅱ、Ⅲ)对太阳轮、内齿圈、行星架以及行星轮动态响应的影响。由于缺少相关试验数据,在后续分析讨论中,本文以模型Ⅰ的计算结果作为参考基准。
根据三种滑动轴承模型,分别建立行星轮系动力学模型,计算行星轮滑动轴承油膜力,如图8所示。由图8可知,应用三种滑动轴承模型计算的行星轮切向油膜力(Fy)幅值及波动基本一致,但徑向油膜力(Fx)幅值及波动存在一定差异,主要原因是模型Ⅱ、Ⅲ在对滑动轴承解耦时忽略了径向载荷波动的影响。此外,模型Ⅱ、Ⅲ计算的油膜力基本一致,表明对刚度阻尼系数修正后的滑动轴承模型(模型Ⅲ)仍适用于动态油膜力预测。
图9所示为应用模型Ⅱ、Ⅲ计算的滑动轴承刚度阻尼系数,图10所示为应用模型Ⅲ计算的附加偏心修正力,图11所示为应用模型Ⅰ、Ⅱ、Ⅲ计算的太阳轮行星轮、内齿圈行星轮动态啮合力。
由图9可知,相比于模型Ⅱ,模型Ⅲ中的刚度阻尼系数会产生明显波动。由图10可知,模型Ⅲ中附加偏心修正力出现周期性波动。这主要是由于行星轮在时变的动态啮合力综合作用下(图11),使得作用在滑动轴承上的等效载荷产生波动,进而影响油膜力,造成刚度阻尼系数波动。这也侧面说明考虑时变的刚度阻尼系数更符合实际情况,有助于提高模型精度。
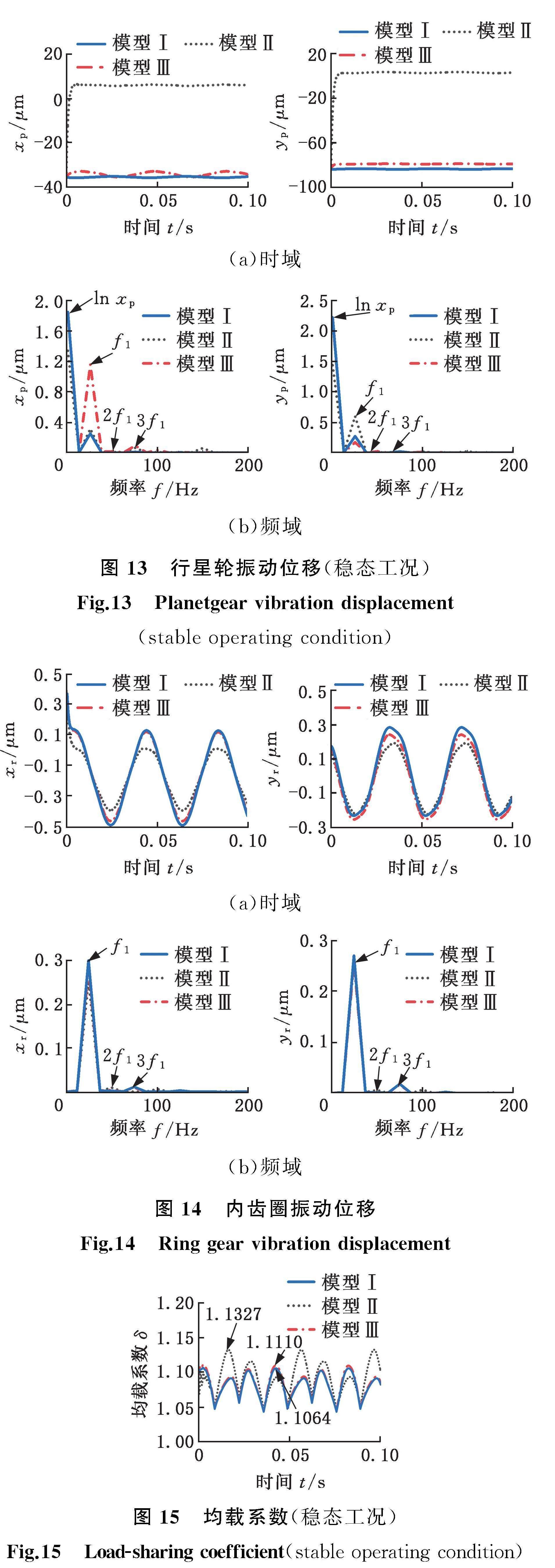
图12~图14所示分别为应用三种滑动轴承模型计算的太阳轮、行星轮、内齿圈振动位移的时域和频域结果,图15所示为应用三种滑动轴承模型计算的均载系数[28]。
由图12~图14可知,各构件特征频率主要集中在啮频及其倍频(nf1,n=1,2,…);整体上,相比于模型Ⅱ,采用模型Ⅲ计算的各构件振动响应更接近模型Ⅰ,尤其是对行星轮振动位移响应计算精度的提高最为明显(图13)。这主要是由于模型Ⅲ考虑了滑动轴承轴颈轴套偏心量对油膜力的影响,因此修正后模型Ⅲ计算的均载系数更接近模型Ⅰ(图15)。
4.3 瞬态工况对比
风速随机性变化会使风电齿轮箱输入转矩产生显著波动。为了验证提出的刚度阻尼修正方法在瞬态工况下的有效性,采用阶跃载荷(100%→75%→100%)模拟风电齿轮箱在实际运行中由于输入转矩时变引起的变速变载瞬态过程,分析行星轮振动响应、动态啮合力与均载系数变化规律。
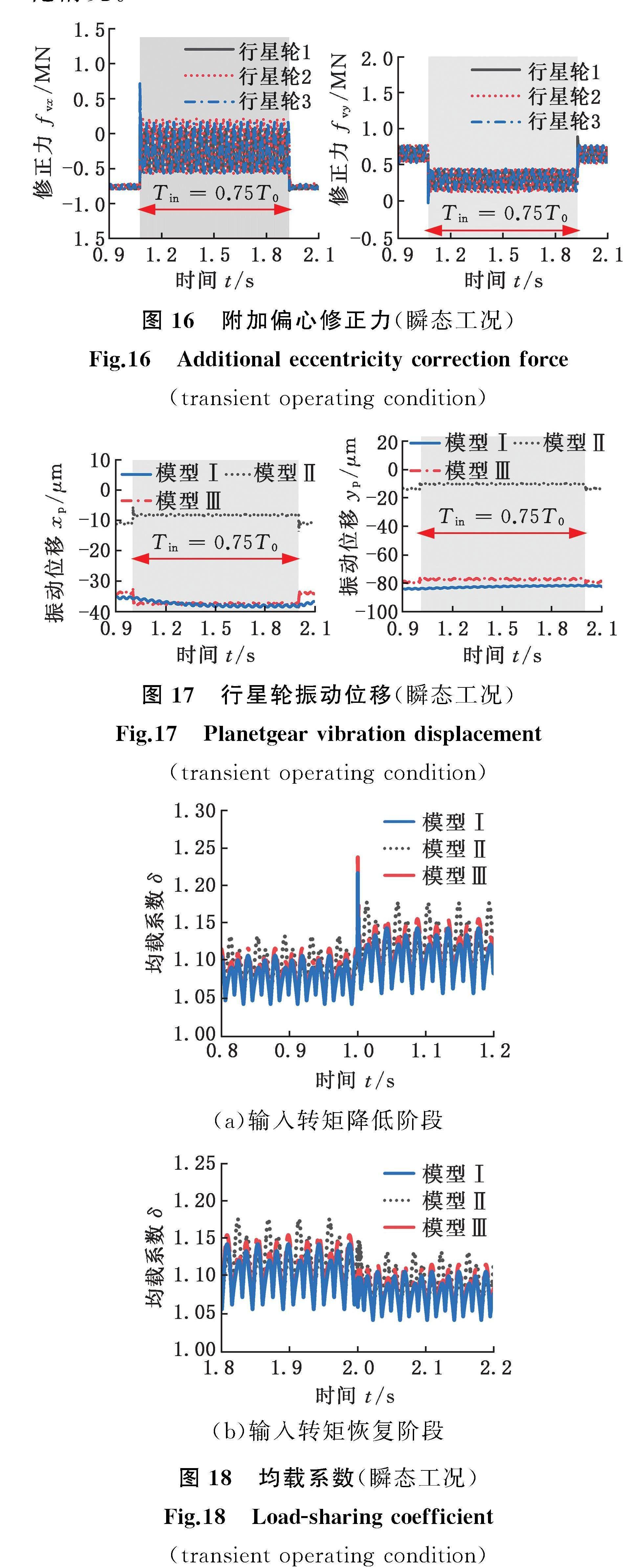
图16所示为应用模型Ⅲ计算的附加偏心修正力,图17所示为应用三种滑动轴承模型计算的行星轮振动响应,图18所示为对应的均载系数变化情况。
由图16可知,输入转矩突变会引起附加偏心修正力产生类似的阶跃波动。由图17可知,在输入转矩突变期间,模型Ⅲ计算的行星轮瞬态振动响应可以很好地跟随模型Ⅰ计算结果。由图18可知,相比于模型Ⅱ,模型Ⅲ计算的均载系数更接近模型Ⅰ,但两者的均载系数均略大于模型Ⅰ的均载系数,主要原因在于模型Ⅱ、Ⅲ采用的刚度阻尼系数是在稳态工况下求解得到的,难以有效捕捉突变工况下油膜力瞬态变化,表现出较大刚性,但整体上提出的刚度阻尼修正方法对瞬态工况仍具有很好的适用性。
4.4 滑动轴承参数影响
利用计算效率更高且兼顾仿真精度的模型Ⅲ开展了滑动轴承参数敏感性分析。图19所示为额定工况下滑动轴承宽径比r0、间隙Δ对均载系数的影响规律。由图19可知,增大宽径比会增大均载系数,降低均载性能,而减小轴承间隙会减小均载系数,改善均载性能。
4.5 试验验证
为了验证模型Ⅲ的有效性,对某型2MW级风电齿轮箱开展台架均载测试。图20所示为试验台布局与内齿圈齿根应变片测点位置。其中,试验台由主试齿轮箱、陪试齿轮箱、4台电机、联轴器等组成。
通过测试内齿圈齿根应变,推算行星轮系均载系数。在内齿圈等间隔120°的齿槽底部粘贴应变片,每处使用8个应变片;测试设备采用DRA-30A多通道动静态应变仪;采样频率设置为2000 Hz,采样点数为65 000。
考虑到现场实际生产计划与其他产品测试安排,本次试验暂时仅开展额定工况测试。根据现场测试得到的应变数据(图21),可采用下式计算得到均载系数:
δ=Npσmax/∑Npi=1σi(24)
式中,σmax为各测点应变有效值的最大值;σi为各测点应变有效值。
图22所示为50%、75%、100%额定工况下模型Ⅲ计算的均载系数与100%额定工况下试验结果的对比。
由圖22可知,随着输入转矩的增大,均载系数逐渐减小,表明均载性能逐渐提高;100%额定工况下模型Ⅲ计算的均载系数为1.106,试验结果为1.093,仿真误差约1.18%,验证了模型的有效性。
5 结论
(1)齿轮副动态啮合力波动会使滑动轴承刚度阻尼系数和附加偏心修正力产生周期性变化,考虑上述影响,有助于提高模型仿真精度。
(2)在稳态和瞬态工况下,所建立的行星轮系动力学模型可以显著提高系统响应仿真精度,尤其是行星轮振动响应。
(3)减小滑动轴承宽径比与轴承间隙有助于减小均载系数,提高均载性能;增大输入转矩会改善均载性能。
参考文献:
[1] LUND J W, ARWAS E B, CHENG H S, et al. Rotor-bearing Dynamics Design Technology, Part Ⅲ:Design Handbook for Fluid Film Type Bearings[R]. OH:Air Force Aero Propulsion Laboratory, 1965.
[2] LUND J W. The Stability of an Elastic Rotor in Journal Bearings with Flexible, Damped Supports[J]. Journal of Applied Mechanics, 1965, 32(4), 911-920.
[3] LUND J W. Calculation of Stiffness and Damping Properties of Gas Bearings[J]. Journal of Tribology, 1968, 90(4), 793-803.
[4] MAJUMDAR B C, PAI R, HARGREAVES D J. Analysis of Water-lubricated Journal Bearings with Multiple Axial Grooves[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2004, 218(2):135-146.
[5] YANG L, LI H, YU L. Dynamic Stiffness and Damping Coefficients of Aerodynamic Tilting-pad Journal Bearings[J]. Tribology International, 2007, 40(9):1399-1410.
[6] YANG L, QI S, YU L. Analysis on Dynamic Performance of Hydrodynamic Tilting-pad Gas Bearings Using Partial Derivative Method[J]. Journal of Tribology, 2009,131(1):011703.
[7] HUSSEIN S, TAMER E S. Nonlinear Dynamics and Bifurcation Analysis of Journal Bearings Based on Second Order Stiffness and Damping Coefficients[J]. International Journal of Nonlinear Mechanics, 2022, 142:103972.
[8] TAMER E S, HUSSEIN S. Bifurcation Analysis of Rotor/Bearing System Using Third-order Journal Bearing Stiffness snd Damping Coefficients[J]. Nonlinear Dynamics, 2022, 107(1):123-151.
[9] YANG J, ZHU R, YUE Y, et al. Nonlinear Analysis of Herringbone Gear Rotor System Based on the Surface Waviness Excitation of Journal Bearing[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2022, 44(2):54.
[10] CHANDAN K, SOMNATH S. Dynamic Response of an Unbalanced Rigid Rotor Bearing System with a Nonlinear Hydrodynamic Force[J]. Journal of Computational and Nonlinear Dynamics, 2018, 13(9):090909.
[11] DAKEL M, BAGUET S, DUFOUR R. Nonlinear Dynamics of a Support-excited Flexible Rotor with Hydrodynamic Journal Bearings[J]. Journal of Sound and Vibration, 2014, 333(10):2774-2799.
[12] ZHANG C, WEI J, WANG F, et al. Dynamic Model and Load Sharing Performance of Planetary Gear System with Journal Bearing[J]. Mechanism and Machine Theory, 2020, 151:103898.
[13] ZHANG H, CAO S, LI P, et al. Mesh and Variable Bearing Dynamic Coefficients[J]. Shock and Vibration, 2022, 4132673.
[14] YANG J, ZHU R, LEE H, et al. Experimental and Numerical Dynamic Analysis of Marine Herringbone Planetary Gearbox Supported by Journal Bearings[J]. Journal of Sound and Vibration, 2023, 545:117426.
[15] YIN M, CHEN G, SU H. Theoretical and Experimental Studies on Dynamics of Double-helical Gear System Supported by Journal Bearings[J]. Advances in Mechanical Engineering, 2016, 8(5):1687814016646977.
[16] YANG J, YUE Y, ZHU R, et al. Dynamic Characteristics of Encased Differential Gear Train with Journal Bearing[J]. Mathematical Problems in Engineering, 2020(1):2436191.
[17] HAGEMANN T, DING H, RADTKE E, et al. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part Ⅰ:Basic Relations[J]. Lubricants, 2021, 9(10):97.
[18] HAGEMANN T, DING H, RADTKE E, et al. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part Ⅱ:Impact of Structure Deformation[J]. Lubricants, 2021, 9(10):98.
[19] LUND J W. Review of the Concept of Dynamic Coefficients for Fluid Film Journal Bearings[J]. Department of Machine Elements, 1987, 109(1):37-41.
[20] CUI S, GU L, WANG L, et al. Numerical Analysis on the Dynamic Contact Behavior of Hydrodynamic Journal Bearings during Start-up[J]. Tribology International, 2018, 121:260-268.
[21] SOMEYA T, MITSUI J, ESAKI J, et al. Journal-bearing Databook[M]. Heidelberg:Springer Science & Business Media, 2013.
[22] 譚建军,伍源,白杨,等.考虑环境参数的风电齿轮箱传动系统疲劳性能优化[J].机械传动,2023,47(8):53-63.
TAN Jianjun, WU Yuan, BAI Yang, et al. Optimizationof Fatigue Performance of Wind Turbine Gearbox Transmission System Considering Environmental Parameters.[J]. Journal of Mechanical Transmission,2023,47(8):53-63.
[23] TAN J, ZHU C, SONG C, et al. Effects of Flexibility and Suspension Configuration of Main Shaft on Dynamic Characteristics of Wind Turbine Drivetrain[J]. Chinese Journal of Mechanical Engineering, 2019, 32:1-15.
[24] XIE S, JIN X, HE J. Structural Vibration Control for the Offshore Floating Wind Turbine Including Drivetrain Dynamics Analysis[J]. Journal of Renewable and Sustainable Energy, 2019, 11(2):023304.
[25] LIU C, QIN D, LIAO Y. Dynamic Modeling and Analysis of High-speed Planetary Gear Including Centrifugal Force[J]. Journal of The Brazilian Society of Mechanical Sciences and Engineering, 2017, 39:3769-3778.
[26] 钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2):131-136.
ZHONG Wanxie. Fine Time Integration Method for Structural Dynamic Equations[J]. Journal of Dalian University of Technology, 1994, 34(2):131-136.
[27] DAKEL M, BAGUET S, DUFOUR R. Nonlinear Dynamics of a Support-excited Flexible Rotor with Hydrodynamic Journal Bearings[J]. Journal of Sound and Vibration, 2014, 333(10):2774-2799.
[28] TAN J, LI H, TANG H, et al. Dynamic Modeling and Analysis of Planetary Gear Train System Considering Structural Flexibility and Dynamic Multi-teeth Mesh Process[J]. Mechanism and Machine Theory, 2023, 186:105348.
(編辑 袁兴玲)
作者简介:
唐 浩,男,1998年生,硕士研究生。研究方向为滑动轴承风电齿轮箱动力学。E-mail:202107131327@stu.cqu.edu.cn。
谭建军(通信作者),男,1991年生,副研究员。研究方向为齿轮传动系统动力学、减振优化。E-mail:jianjuntan@cqu.edu.cn。

