基于混沌粒子群优化算法的反应釜温度预测控制研究

雷 江,唐晓伟,徐 兵

(1.浙江普洛家园药业有限公司,浙江 东阳 322118;2.上海应用技术大学电气与电子工程学院,上海 201418)

0 引言

在传统的化工生产领域中,反应釜是生产产品的主要容器。在反应釜反应过程中,其温度因具有非线性[1]、大滞后等特性而导致会偏离设定值,所以精准的温度控制方法一直是化工行业的难题。针对非线性控制问题,许多学者提出了先进的控制器。该控制器利用智能优化算法优化控制器参数以实现对反应釜温度的精确控制[2-5]。苗荣霞等[6]利用动态矩阵控制(dynamic matrix control,DMC)-比例积分微分(proportional integral differential,PID)串级控制算法优化腐殖酸液肥反应釜温度。与传统PID控制算法相比,该方法的超调量明显缩小,具有很好的控制效果。覃溢波等[7]提出了一种基于粒子群优化(particle swarm optimization,PSO)的高斯过程回归模型,以预测反应釜的出料浓度,并利用粒子群算法代替共轭梯度法优化模型超参数的方法。试验结果表明,该方法能有效提高反应釜出料浓度预测精度。金晓明[8]等提出了一种自抗扰控制器。该控制器具有控制精度高和鲁棒性强的优点。

基于以上学者研究的理论基础,本文针对化工生产反应釜温度控制精度不高导致生产效率低以及DMC参数选取困难的问题,采用Tent 映射的混沌粒子群优化(chaotic particle swarm optimization,CPSO)算法和动态矩阵预测模型结合的控制策略,以提高DMC参数寻优的速度,并将其与PID、DMC-PID算法进行仿真试验对比。超调量、调节时间等动态指标对比结果表明,本文提出的基于CPSO的DMC-PID算法对反应釜温度控制具有较好的控制效果。

1 工艺过程分析

工业生产过程具有较强的多变量和非线性的特点,需要考虑多方面的因素才能设计出全面的控制策略。控制组态界面如图1所示。

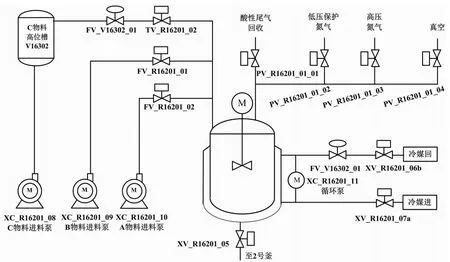
图1 控制组态界面

图1中:A物料为二氯甲烷;B物料为甲酰胺;C物料为草酰氯。

主要生产需求控制如下。

①各项指标稳定。釜内压力、温度保持在一定值内。

②温度的偏差为±2 ℃。

反应的化学方程式如下。

主反应为:

(1)

式中:D为主反应的生产混合物。

副反应为:

(2)

式中:E为副反应的生产混合物。

釜内具体反应过程如下。

①对反应釜进行氮气保护。这是为了让反应釜内充满氮气,以隔绝空气。只有当反应釜内氮气压力达到50 kPa后,才能进行物料反应。

②分别向釜内泵入一定比例的A、B两种物料。A、B两种物料充分搅拌混合后会大量放热。放热时,调节冷却水会流入反应釜周围的夹套,从而达到降温的目的。釜内温度需要保持在50 ℃。只有在一定温度内反应出来的原料才是合格的产品。

③当反应釜温度达到50 ℃时,将高位槽泵入一定量的C物料以待用。C物料作催化剂使用。当物料温度达到催化温度时,将高位槽C物料转移至反应釜内进行化学反应。转移完毕后,保温2 h。

此时,第一部分的原料已经生产出来,由反应釜底部的出料阀输送至第二个釜进行加工。由上述工艺过程可以看出,反应温度对产品质量有非常大的影响。

2 反应釜模型建立

反应釜结构如图2所示。由图2可知,反应釜主要由反应容器、搅拌装置和夹套三大部分组成。反应容器为一个钢制的罐型容器。物料从加料口投放或者通过固体投放器吸入容器内。搅拌装置由搅拌器和搅拌电机等组成。夹套包裹在容器的外围,用于控制反应釜的釜内温度。当需要降温时,混合液(冷媒)进入夹套吸走釜内热量,以达到降温效果。

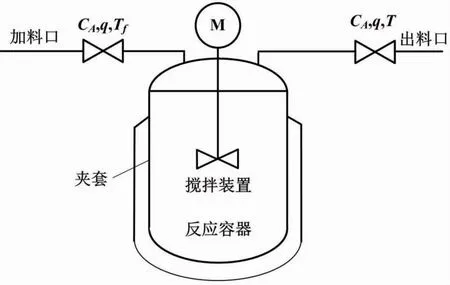
图2 反应釜结构图

根据阿伦尼乌斯定律可得出化学反应的过程。假设物料完美混合、体积不变、热容不变等,反应釜的能量平衡方程如下。

(3)

式中:CA为进料浓度,mol/L;t为时间,s;T为温度,K;Q为流量,L/min;V为反应釜的体积,L。

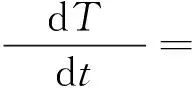
(4)

式中:ρ为密度,Kg/m3;Tjt为反应釜的夹套温度,K;Ar为热交换表面的面积,m3;Cp为比热容,其值为1 cal/(kg·K)。

每单位体积的反应速率为:

(5)

式中:rA为反应釜的反应速率,mol/ (L·min);k为速率,s;E为活化能,K;R为气体常数,J/(mol·K);k0为频率因子,min-1。

夹套的能量平衡方程式为:

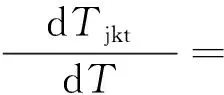
(6)

式中:Qcw为冷媒流量,L/min;Mo为热媒冷媒的质量;Cwater为冷媒的热容,cal/(kg·K);Tcw为冷媒的温度,K。

通过对式(4)和式(6)进行线性化,可以生成一个线性模型。反应釜进料管道的运行参数如下:Q为100 L/min;V为100 L;Tjt为280 K;反应热(-ΔH)为50 000 J/mol;热传递项(由传热系数U和传热面积A组合而成)为200 000 cal/(min·K);k0为7.2e10/min;E为9 980 K;CA为0.082 35 mol/L;Cp为1 cal/(kg·K);R为8.314 5 J/(mol·K);Tcw为350 K。

式(4)和式(6)的非线性模型方程围绕稳定的工作点代入反应釜运行参数,得出的反应釜传递函数为:

(7)

3 温度预测控制策略

因为反应釜温度具有非线性、大滞后的特性,极易受到外部因素影响,所以本文采用DMC-PID控制策略。DMC-PID系统如图3所示。

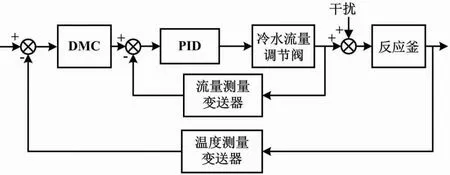
图3 DMC-PID系统框图

控制策略为:首先,利用PID控制消除主要干扰,由DMC控制消除系统的时滞特性;然后,系统的主变量为反应釜温度、副变量为冷却水流量。

3.1 DMC

DMC算法具有三大原理,分别为预测模型、反馈校正和滚动优化。DMC算法利用简单试验即可获得预测模型,能在有限时域进行滚动局部优化,因而具备较好的适应力和较强的鲁棒性。DMC系统如图4所示。

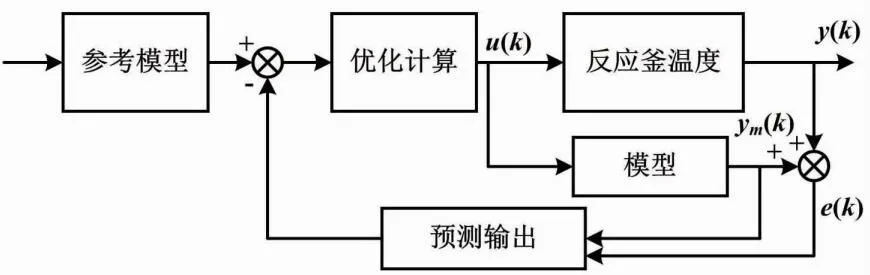
图4 DMC系统框图

DMC的控制机理为:首先,根据在采样周期中所采集到的测量值,求得开环问题的解;然后,将优化解的第一个控制量应用在系统上;最后,在下一个采样周期重复求解过程。多步预估可以解决系统的滞后问题。预测时域会直接影响系统响应速度。

3.1.1 预测模型

预测控制算法是通过控制对象的非参数模型而建立的一种控制算法。该算法主要是在被控对象的过程数据和预期输入的条件上科学计算下一时刻的输出预测,从而展示下一时刻的动态。

预测模型的控制机理为:首先,给反应釜温度控制系统一个简单的阶跃信号,以获得阶跃响应曲线;然后,将得到的值作为动态系数;最后,经过N个周期,系统将逐渐趋于阶跃响应的稳定值。预测模型为:

Ym(k+1)=Y0(k+1)+AU(k)

(8)

式中:Ym(k+1)为k时刻预测增量序列作用时的预测输出量;Y0(k+1)为预测初始值。

ΔU(k)=[Δu(k),Δu(k+1),…,Δu(k+M-1)]T

(9)

式中:Δu(k)为增量序列。

(10)

式中:P为预测时域;M为控制时域的长度;A为由a1,a2,…,aN系统响应序列组成的动态矩阵。

3.1.2 反馈校正

反应釜温度控制的过程中会受到一些外界干扰因素的影响,导致出现模型失配、系统不稳定的情况。为了使预测模型与实际过程一致,需要利用系统过程中的误差信息,不断对输出预测值进行校正,以实现闭环预测。实现步骤为:首先,对误差值进行校正从而得到模型的预测值;然后,预测值经过位移成为下个预测初值。其过程可表示为:

e(k+1)=Y(k+1)-Y(k+1|k)

(11)

输出控制会因为系统模型存在一些不稳定因素而受到影响。对此,可以利用e(k+1)加权修正输出预测值。

(12)

3.1.3 滚动优化

预测控制有限时域仅滚动优化,而非全局离线优化。滚动优化根据解出的最佳输入值使系统无限接近预期值。这种方法可以实时调整干扰带来的影响。对于参考轨迹为yd(k+i)和预测输出为yp(k+i)的系统,二次型滚动优化目标J为:

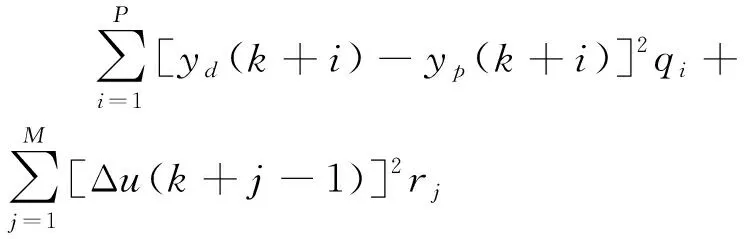
(13)

式中:Δu(k+j-1)为控制增量式;qi、rj均为加权系数。

3.2 CPSO算法

PSO算法的灵感来自模拟鸟群觅食的智能优化算法。PSO算法的特点是收敛快、有较好的全局搜索能力、可以克服系统的滞后性。但PSO算法会存在精度比较低的缺点。如果系数加速,粒子容易丢失最优解。在收敛过程中,所有粒子都飞向最优解,会使得粒子失去多样性,导致速度变慢。在求解过程中,粒子需要不断更新个体和全局极值,从而找到最优解。更新式为:

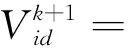
(14)

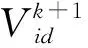
(15)

由于PSO算法收敛慢、局部搜索能力弱,不能较好地得出准确的结构。CPSO借助混沌理论[9-11]引入粒子速度的更新过程,使系统呈现混沌特点。其主要思想是将常规随机序列转换成混沌序列,以提高收敛精度和速度。

3.3 混沌Tent映射

混沌是一种持续的不规则状态。在不加随机因子的情况下,利用混沌运动的遍历性和当前粒子群搜索到的最优位置产生混沌序列,能够有效避免陷入局部最优解的状态,以获得全局最优解。Logistic[12]方程为:

Xn+1=μXn(1-Xn)

(16)

式中:μ为控制变量;Xn为混沌序列。

当μ=4时,系统处于完全混沌状态。

Logistic映射的混沌序列为不均匀分布,会对搜索的速度造成一定影响。因此,本文采用Tent映射,从而在搜索空间内生成分布均匀的初始种群。混沌Tent映射模型为:

(17)

3.4 DMC参数

DMC算法的各参数对系统性能有不同的影响。P对系统的快速和稳定性造成影响。M对系统的跟随性、鲁棒性有一定程度的影响。R限制控制量的剧烈变化。h在受到模型失配时会对系统有一定的控制作用。DMC的控制参数整定采用试凑方法。试凑方法浪费时间且不是最优参数,导致控制效果差。因此,本文采用Tent映射的CPSO算法优化DMC参数P、M、R、h。优化DMC算法流程如图5所示。

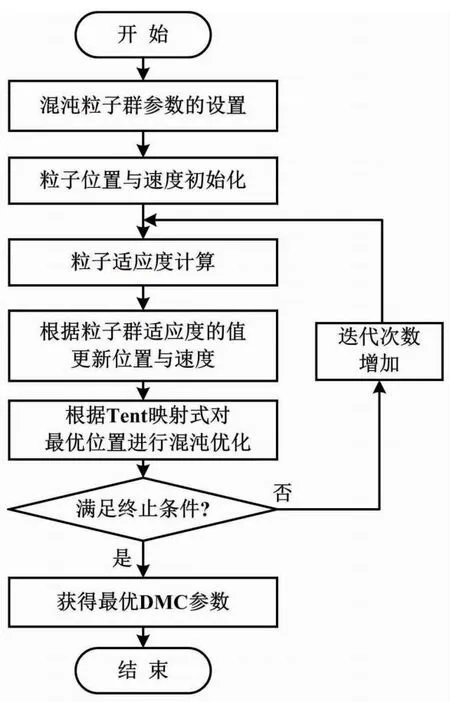
图5 优化DMC算法流程图

4 系统仿真与结果分析

4.1 Tent映射CPSO算法试验分析

仿真试验环境如下。中央处理器(central processing unit,CPU)为Intel Core i5-1130H。操作系统为Windows 11。处理器速度为3.10 GHz。内存为16 GB。编程环境为Matlab R2018b。

为验证CPSO算法的有效性,本文将其与PSO算法进行比较试验。迭代次数对比如图6所示。

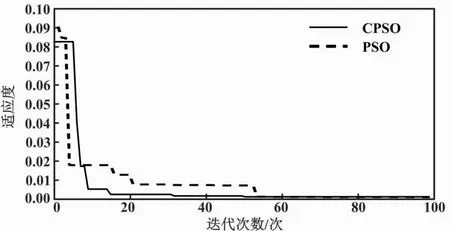
图6 迭代次数对比

由图6可知,CPSO迭代次数具有显著提升,并且适应值更小。综上所述,CPSO算法局部的搜索时间更短,验证了CPSO算法的性能优于PSO算法。这主要得益于Tent混沌映射,使CPSO算法可以有效地平衡全局和局部的寻优能力。

4.2 仿真分析

系统阶跃响应曲线如图7所示。

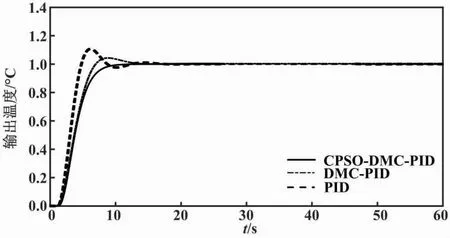
图7 系统阶跃响应曲线

由图7可知:传统PID控制的超调量为10%左右,系统波动较大;采用DMC-PID控制的超调量为5%左右,响应速度较快;CPSO-DMC-PID控制的超调量几乎为0%,输出温度较为稳定。

加入扰动后的系统阶跃响应曲线如图8所示。

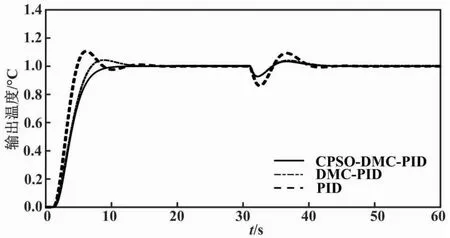
图8 加入扰动后的系统阶跃响应曲线

由图8可知,在抗干扰方面,试验在35 s处加入扰动后,CPSO-DMC-PID控制抑制扰动能力较强,调整速度比传统PID控制和DMC-PID控制更快,完全可以抵抗干扰。

从上述试验结果可以看出,本文提出的CPSO-DMC-PID控制方法的阶跃响应各项性能指标均优于传统控制方法。

5 结论

本文针对工业过程控制系统中的反应釜温度控制,采用CPSO优化DMC-PID控制参数,可以有效提高系统的超调量与响应时间等。与传统的PID和DMC-PID控制相比,CPSO-DMC-PID控制提升了5%的超调量,并在响应时间上具有一定的优势。这说明其具有较好的控制效果与稳定性。仿真结果数据表明,本文提出的CPSO-DMC-PID预测控制方法优于传统控制方法,具有较好的控制效果,可有效应用于反应釜温度控制。