面向国土空间规划的城市引力模型研究
余晓敏,陈翠芳,祁玉杰,吕 婧
(1. 湖北省空间规划研究院,湖北 武汉 430071;2. 自然资源部数字制图与国土信息应用重点实验室,湖北 武汉 430079)
城市群是城市化发展到一定阶段的产物。随着经济全球化与一体化进程不断加快,城市群各城市之间的联系日益加深,人流、物流、资金流、技术流、信息流不停地快速流动和碰撞,推动了城市群社会经济的发展及其空间结构的演变[1-2]。城市关联度分析是城市群国土空间规划编制和实施监督评价的重要内容。当前,城市关联度测算主要基于城市引力模型,涉及城市质量指数和城市距离指数测算2个方面[3]。国内学者对此做了相关研究,陈文贤[4]从城市竞争力的角度选取指标构建城市质量的评价指标体系来计算城市质量。李远和[5]从空间直线距离、交通时间成本和交通货币成本3个方面综合计算交通距离。郭源园[6]等通过增加吸引惯性指数来改进城市引力模型计算公式。钱春蕾[7]等引入相对引力常量来反映城市间经济联系的变化规律。但目前的研究中仍存在一些问题,如城市质量指数仅采用单一或少数指标测算,不能完全反映城市质量综合状况,且考虑城市经济、人口、基础设施、人文环境等方面的影响因素较多,国土空间影响因素不足;城市距离指数主要基于城市之间的直线距离测算,不能准确反映城市之间的实际交通联系状况;传统的城市引力模型难以挖掘国土空间要素与城市关联度的内在联系[8]。
本文将构建面向国土空间规划的城市引力模型,在城市质量指数测算中加入交通运输用地面积及占比、建成区路网密度、建成区绿化覆盖率等要素,在城市距离指数测算中加入铁路网和公路网密度、铁路和公路交通通行最短时间等要素,使城市关联度的测算结果更加科学合理。同时,基于此模型开展湖北省城市群城市空间联系及时空变化特征分析,为湖北城市群规划编制与调整以及规划实施监督和管理决策提供更加科学的信息服务支持。
1 城市引力模型介绍
城市引力模型以牛顿经典力学的万有引力公式为基础,是城市地理学与区域经济学中研究城市空间关系十分重要的模型,也是研究区域空间关系的核心工具[9-10]。城市引力的计算涉及到城市质量和城市距离2个方面。
城市引力模型基本公式如下:
式中,Rij为城市i与城市j之间的引力;mimj为城市i与城市j的城市质量;dij为城市i与城市j之间的距离;b为距离衰减指数;k为引力系数,一般k取1,b取2。
城市质量实质上是城市综合实力的表现,采用城市竞争力模型来衡量城市质量,通过建立评价城市质量的指标体系来确定城市质量的大小,优化城市质量计算,城市质量计算公式如下:
式中,Wif和Pit为i城市中第f种影响城市质量的指标因子的权重和指标量化值。
城市之间的距离指数受多种因素影响,通过构建评价距离指数的指标体系来确定距离指数的大小,优化距离指数的计算,距离指数计算公式如下:
式中,Wijf和Pijt为i 和j 城市中第f种影响交通距离的指标因子的权重和指标量化值。
综合上述城市质量和距离指数的计算公式,最终确定城市引力模型计算公式为:
2 指标体系构建与计算
2.1 城市质量指标体系构建
城市质量实质上是城市综合实力的表现,从资源要素流动规律来看,确定各城市相对于其他城市综合实力的好坏程度可通过分析城市与其他城市的相互补充与需求程度得出,即对城市竞争力的分析,因此城市综合实力又可以看作是城市的竞争力。基于此,本模型采用城市竞争力模型来衡量城市质量,通过建立评价城市质量的指标体系来确定城市质量的大小,从人口、经济、社会、生态、交通和旅游6 个方面来选取指标[11]。城市的人口规模越大,人口越集中,城镇化水平越高,就会吸引其他城市的人员流入集中;城市的经济状况越发达,资金流集中,则会吸引其他城市更多的资金汇聚于此,获取更大价值,也会吸引其他城市的人前来发展经济;城市的社会生活水平高,人均可支配收入高,教育医疗条件良好,基础设施完备,会形成一定的吸引力;城市的生态环境良好,绿化条件好,空气质量优良,会吸引其他城市的居民前来休闲度假,促进2 个城市的联通;城市的对外交通设施完备,有利于促进与其他城市的往来;城市的旅游业发达,会促进城市的人员往来[12]。具体指标项如表1所示。

表1 城市质量指标体系表
2.2 交通距离指标体系构建
在以往的研究中,通常使用空间直线距离、时间成本和货币成本其中的一项或几项指标来测算距离,但是并不能体现城市在空间上的联系,并且指标过于单一,不能全面地反映城市之间的距离,因此本模型从空间角度出发,从铁路、公路和空间距离方面选取指标,构建交通距离指标体系,综合评价交通距离。交通距离指标体系如表2所示。

表2 交通距离指标体系表
2.3 指标权重计算
由于本模型构建的城市质量指标体系和交通距离指标体系都含有多个指标,因此利用主成分分析法来计算指标权重[9]。主成分分析法也称为主分量分析法,旨在利用降维的思想,把复杂的多指标转换为较少的综合性指标。在用统计方法研究多变量问题时,变量太多会增加计算量和分析问题的复杂性,主成分分析法可以避免这一问题。
提取主成分是指将原有多个相关性较强的变量x1、x2、…、xn重新组合,生成几个少数的不相关的变量F1、F2、…、Fp,使其尽可能多地提取原有变量的信息。其中F1、F2、…、Fp就是主成分,分别为第一主成分、第二主成分、...、第p主成分。
2.4 指标归一化处理
城市质量和交通距离指标体系中的指标类型不尽相同,城市质量指标皆为极大型指标,且城市质量在城市引力计算公式中作分子,指标值越大越好,因此不需要进行转换。交通距离指标体系中路网最短时间和空间直线距离为极小型指标,路网密度为极大型指标,且交通距离在城市引力计算公式中作分母,指标值越小越好,因此需要将公路网密度指标和铁路网密度指标转换为极小型指标。本模型采用取负值的方法将极大型指标转换为极小型指标。
城市质量和交通距离指标体系都为多指标评价体系,各评价指标的量纲和数量级都不同。如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用。因此,为了保证结果的可靠性,需要对原始指标数据进行归一化处理[13-14]。
本模型应用比例变换法来进行归一化处理,变化公式为:
式中,x为标准化的指标数值;X为原始指标数值;Xmax为历年的指标最大值,为了使不同年份的城市关联度可以进行比较,要选择同样的标准进行归一化处理,因此Xmax选择所有年份中的指标最大值。
3 基于城市引力模型的城市关联度测算
城市关联度测算常用于分析城市的联系紧密度,主要基于城市引力模型,计算两两城市之间的城市引力。城市引力强度反映了城市对外联系量和空间相互作用程度的大小,2 个城市的城市引力强度越大,表明城市间空间相互作用程度和联系程度也就越深。通过城市关联度时空变化及其原因分析,可以为城市群规划实施评价和调整提供技术支撑。技术流程如图1所示。
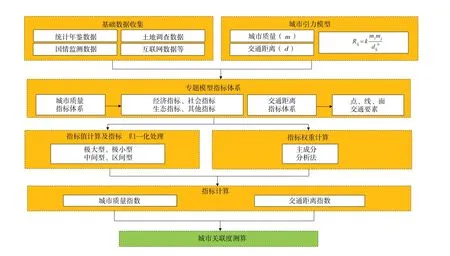
图1 基于城市引力模型的城市关联度测算技术流程
4 实验结果与分析
本文以湖北省的3个城市群为实验范围,包括位于湖北省东部的武汉城市圈(以武汉为圆心,覆盖黄石、鄂州、黄冈、孝感、咸宁、仙桃、天门、潜江等周边8个大中型城市),位于湖北省西北部的“襄十随神”城市群,以及位于湖北省西南部的“宜荆荆恩”城市群。城市质量指标数据主要来源于城市统计年鉴、城市建设统计年鉴和土地变更调查数据。交通距离指标数据来源于湖北省地理国情监测数据,基于铁路网和公路网矢量数据进行路网分析和计算获得。将城市质量指数和交通距离指数代入公式(4)计算得到各城市群的城市关联度。将各城市与其他城市的关联度进行加总,得到每个城市的城市关联度指数,分别如图2、3、4所示。

图2 武汉城市圈城市关联度指数图
从图2 可以看出武汉城市圈中武汉市的城市关联度指数明显高于其他城市,鄂州市、孝感市和黄冈市的城市关联度指数较高,仙桃市、潜江市和天门市的城市关联度指数较低。武汉市和仙桃市的关联度指数增长的最快,黄石市和咸宁市的关联度指数增长的最慢。从图3 可以看出“襄十随神”城市群中襄阳市和随州市的城市关联度指数较高,神农架林区的城市关联度指数明显低于其他城市。襄阳市和随州市的关联度指数增长得最快,神农架林区的关联度指数增长得最慢。从图4 可以看出“宜荆荆恩”城市群中宜昌市、荆州市和荆门市的城市关联度指数较高,恩施州的城市关联度指数明显低于其他3 个城市。荆州市的关联度指数增长得最快,恩施州的关联度指数增长得最慢。通对比验证,本模型计算结果与百度人口迁徙数据较为吻合[15]。将3个城市群2 a的城市关联度分别进行可视化,绘制成模型专题图,如图5、6所示。
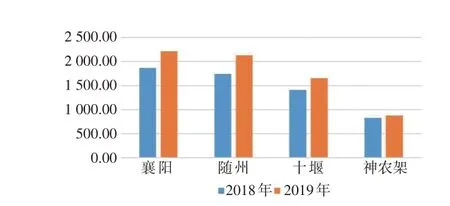
图3 “襄十随神”城市群城市关联度指数图
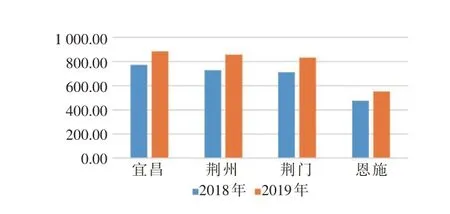
图4 “宜荆荆恩”城市群城市关联度指数图

图5 2018年湖北省城市群城市关联度图
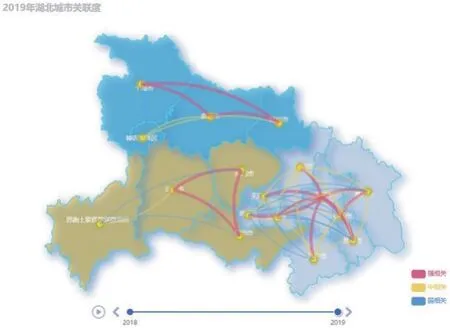
图6 2019年湖北省城市群城市关联度图
从整体来看,武汉城市圈城市关联度的分布特征是以武汉市为引力中心,形成一个向外辐射的联系网,武汉市与其他城市的关联度都较强;在小区域范围内,黄冈市、孝感市、鄂州市和黄石市之间的联系也较强;仙桃市、潜江市和天门市内部之间联系较强,但是与其他城市之间的关联度较弱。“襄十随神”城市群中襄阳市、随州市和十堰市之间的联系比较紧密,神农架林区与其他城市的关联度较弱。“宜荆荆恩”城市群中宜昌市、荆州市和荆门市之间的联系比较紧密,恩施、荆州与其他城市的关联度较弱。
从图5、6 的变化趋势中可以看出武汉-仙桃、武汉-天门、武汉-潜江、仙桃-天门、仙桃-孝感的城市关联度增长较快。襄阳-随州和十堰-随州的城市关联度增长较快,襄阳-神农架和十堰-神农架的城市关联度增长较慢。荆州-荆门和宜昌-荆州的城市关联度增长较快,恩施-荆州和恩施-荆门的城市关联度增长较慢。
由于城市关联度与城市质量指数呈正比,与城市距离指数呈反比。其中,城市质量指数主要与城市GDP、城市人口和交通用地面积有关。因此,建议各城市根据其城市质量指数和距离指数实际情况,因地制宜地制定城市发展策略,如仙桃市、潜江市和天门市等城市质量指数较低的城市,应注重出台政策促进GDP、人口及对外交通用地等城市体量指标适度扩大规模;神农架林区、恩施州等城市距离指数较低的城市,应注重加强铁路、公路等区域交通基础设施建设,提升城市之间交通便利程度。
5 结语
本文对传统城市引力模型进行了改进,增加了交通运输用地面积及占比、建成区路网密度、建成区绿化覆盖率、铁路网和公路网密度、铁路和公路交通通行最短时间等国土空间要素,使城市关联度测算考虑因素更加全面,测算结果更加科学合理。同时,该模型还可以对城市关联度指数与国土空间要素的内在联系进行分析,为城市群规划编制与调整以及规划实施监督和管理决策提供更加科学的信息服务支持。本文仅针对湖北省城市群国土空间专项规划的编制和评估开展了城市引力模型研究和城市关联度测算,下一步将根据总体规划、专项规划、详细规划等不同类型规划的特点,结合不同层级规划的目标和任务要求,探索城市引力模型研究。

