教育传播大数据可视化分析

廖志平

（湖南环境生物职业技术学院，湖南 衡阳 421005）

大数据技术是科学家研究的热点[1]。云计算是在计算机中使用编程模型（Mapreduce）来工作的，包括根据相关计算进行数理分析，将数据来源归入各族群、利用各种数据来源测量数据的相似度和绘制数据，大规模数据分析与云计算有关。

目前，教育数据冗杂，信息量大，大数据技术在教育实践中十分重要。教育数据可为教师、学生、教育管理者、父母和教育研究人员提供以下服务。1）提供直接数据服务，例如基本信息、考试成绩和课堂情况等，通过分析数据，可以掌握学生的特征与学习需求，从而对不同学生进行个性化教学，通过统计数据发现学生在学习中存在的问题，从而改进教育方法，提升教师的教学水平，达到更好的教学效果。2）提供间接数据服务，包括成绩排名、及格率和优良率等。在教学活动的全过程中，教育大数据是提高教育质量和教育管理能力的关键。

1 教育传播大数据可视化流程以及算法

由于大数据技术的应用越来越广泛，其含义也越来越丰富，因此无法精确地界定大数据[2]。大数据并不必然包括大量的数据，但是它们之间存在关联。当前大数据的4V概念已经得到了普遍认可，4V主要包括以下4个方面的内容。1）数据真实性（Veracity），品质。2）数据容量（Volume），根据资料数量和可能的资讯而定。3）数据种类（Variety），数据不同类型。4）传输速度（Velocity），获得数据的速度。

1.1 教育传播大数据可视化流程

教育数据来源各异，因此，对其进行深入研究与发掘不仅需要专业的资料分析人员，更需要教师主动介入[3]，本研究目的是挖掘资料数据。双方经过沟通，明确挖掘对象，提供有针对性的挖掘服务。研究主要包括抽样选取、评估指标、整理有关因子、筛选样本资料、检验并整理符合条件的发掘需求、尝试发掘（运用回归、分类、聚类和关联等）和发掘其他内在属性的性质[4]。将研究结果以可视化的方式呈现，并说明其意义，方便未来评估与介入，教育传播大数据可视化流程如图1所示。分析和挖掘数据是一个不断重复的过程，以便从中挖掘新的需求。

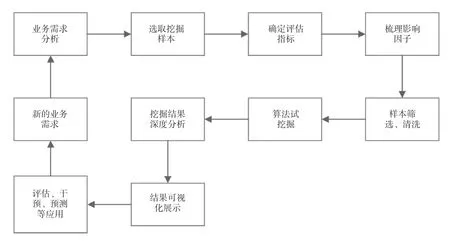
图1 教育传播大数据可视化流程图

1.2 教育传播大数据可视化相关算法

1.2.1 FCM聚类算法

FCM聚类算法（Fuzzy-c-Means algorithm，FCM）[5]的基本原理是模糊理论，这种理论从客观事实出发，处理模糊不确定的实物，又称为模糊C均值算法。

FCM将n个用户数据作为n个向量Xi，其中涉及隶属关系，为一种表示模糊集合的方式。FCM模糊隶属程度的取值范围为[0，1]，在数学上可以将模糊隶属程度进行分类，构建相应矩阵，表示其聚类情况。采用FCM 聚类算法构建模糊矩阵U，在矩阵中每个要素都是各矢量的模糊隶属度，值的范围在[0，1]，归类后的每个元素的模糊隶属度之和均为1。

FCM聚类算法如公式（1）所示。

FCM聚类算法的目标函数如公式（2）、公式（3）所示。

式中：uij的取值范围为[0，1]；ci为模糊类I的聚类中心；dij为第I个聚类中心到第j个向量之间的欧式距离；m为加权指数，其取值范围为[1，∞]。

为使目标函数取得最小值，进行以下改进，如公式（4）所示。

式中：λj为n个约束式的拉格朗日因子。

目标函数取得最小值需要前提，表明其必要条件，如公式（5）所示。

FCM聚类算法包括以下4个步骤（如图2所示）。1）求解各矢量的模糊隶属关系，构造1个[0，1]的初始模糊矩阵U，保证各类别矢量的隶属性和等于1。2）确定聚类的簇集中心。3）对该设计进行优化，确定优化后的算法。4）求得1个新的矩阵U。判断目标函数是否小于固定阙值，如果未达到，那么返回步骤二，反复循环，直至达到要求。

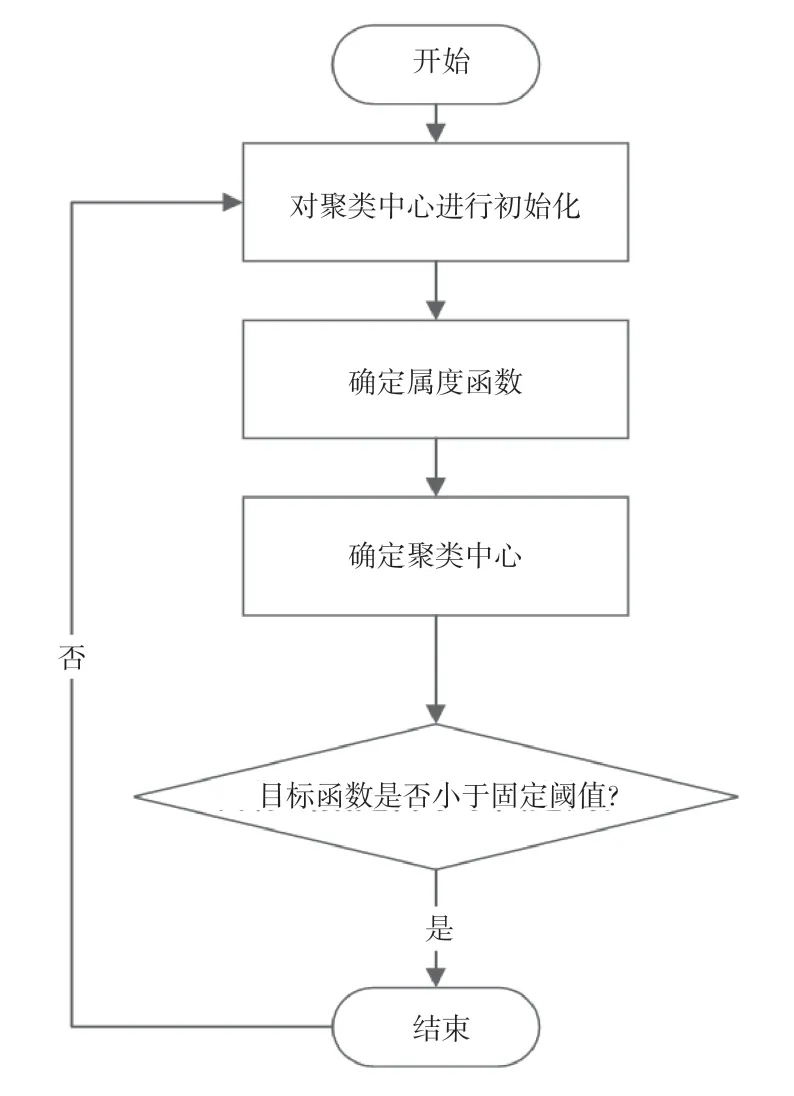
图2 FCM聚类算法的流程图

1.2.2 特征选择算法

特征选择（Feature Selection）是用相关特征来描述一个应用领域的方法[6]。在数学形式上，特征选择可定义为从N个原始特征中选择一个包括M（M≤N）个相关特征的最小子集，使包括M个特征的子集中不同类别的概率分布值接近N个原始特征。如果FN为原始特征集，FM为选出的特征子集，则可能的类别C，条件概率P（C|FM=fM）应当与P（C|FN=fN）接近，其中fM和fN为相应的特征矢量FM和FN的值矢量。在样本数量较多的情况下，采用高效的特征选择方法可以降低样本的维数，为后续的数据分析提供方便。

1.2.3 mRMR算法

最大相关最小冗余算法（Maximum Relevance Minimum Redundancy，mRMR）根据互信息极大化原则，在选取属性后，尽量保存大部分分类信息，同时降低各属性间的相关性。从原始特征集合{t1，t2，t3，...，tn}中选择一个特征子集{t'1，t'2，t'3，...，t'n}构成新的特征空间，并提出新的特征子集，在该子集上，各属性和各属性间的相关系数均尽量变小。特征的相关性用互信息I衡量，如公式（6）所示。

式中：I（x，y）为特征相关性；xi、yj为随机变量；p（xi，yi）为概率密度函数；p（xi）为xi的概率密度函数；p（yj）为yj的概率密度函数。

首先，利用互信息计算I（x，y），I（x，y）越大，它们之间的关联度就越大。先找出包括m{xi}个特征的特征子集S，使m个特征和类别C的相关性最大，即与c关系最密切的m个特征。其中，D为特征与目标的互信息值，|S|为特征集合中特征的个数，S为m个平均互信息最大的集合。maxD，D为特征与目标的互信息最大化，如公式（7）所示。

其次，消除m个特征之间的冗余，其中，R为特征之间的互信息值，minR，R为特征之间的互信息最小化，如公式（8）所示。

求得最大相关度—最小冗余度maxΔMID，ΔMID，如公式（9）所示。

通过上述运算，可以得到ΔMID值的特性，根据这些数值来分类这些特性，达到筛选目的。

2 教育传播大数据可视化

2.1 设计目标

教育大数据可视化系统的目标是在时间短、成本低的前提下，分析并展示在线平台的数据，侧重点为数据的可视化，但是这种可视化平台已经有丰富的商业产品和众多图表展示，系统可以自定义定制要实现的功能点和数据分析维度，系统使用大数据组件开源技术，搭建单节点Hadoop集群，使用MapReduce分析数据，由于市面上大屏可视化系统需要收费，因此用ECharts技术展示数据图表，降低经济成本。

2.2 功能设计

登录注册功能。用户进入登录页，没有注册的用户可以进行注册，已有账号的用户登录后系统显示已登录用户名，点击注销用户可以退出登录。

数据预处理功能。将数据通过开源工具导入分布式基础架构（Hadoop）中的分布式文件系统（HDFS），使用MapReduce处理数据，并将处理好的数据保存至开源数据库（HBase）中。

每日登录人数分析。读取HBase中的登录数据，页面可以显示每月登录人数和不同月份的登录人数对比。

平均学习时长和学习行为次数分析。读取HBase中的相关数据，页面显示不同日期对应的学习时长和学习次数。

每日活跃情况分析。可用柱状图显示每日活跃学生人数，设定每日至少进行3次学习行为的用户为活跃用户。

分时段学习人数分析。可用热力图显示学生在什么时间段爱学习。

2.3 数据处理

数据处理部分是开发MapReduce，用户只需利用Mapper类和Reducer类封装Map和Reduce函数，由客户端调用，即可实现分布式计算。

2.4 系统实现

当在浏览器中输入系统地址时，系统会验证是否有用户已登录，如果没有则跳转登录页面，有则直接跳转首页。登录页面的动画效果是手写的echarts图标效果，有验证用户名和密码的步骤并提示信息。

大屏可视化界面使用阿里云DataV数据可视化平台，点击每日、每周和每月按钮，对应的折线图和柱状图会联动显示数据。地图显示学生的地区分布人数。气泡图显示不同时间段的学习人数。使用DataV数据可视化平台，数据展示效果更好。系统能够帮助非专业的工程师搭建专业水准的可视化界面，满足多种业务的展示需求。

3 结论

综上所述，教育大数据可视化系统是对在在线教育平台中的学生上课、做作业和提问等多方面、多层次的数据进行数据分析和数据展示。教育大数据能够清晰地反映学生的学习能力、优势学科以及特长，教师能够有针对性地制定教学计划，为学生提供个性化的指导，帮助学生对自己的学习状况有一个全面的认识，并适当安排学习重点。通过分析大数据，教师能够得知每位学生的潜能与需要，针对不同的学生选择不同的教学内容，采用不同的教学方法，提供不同的教学服务；父母能够了解自己的子女在学校的学习和心理健康情况；教育管理者能够了解学生的优缺点，发现学生的问题，及时提供关怀与指导，还可以预测他们的职业发展情况，进行有目的的训练；研究人员能够了解目前的现状和问题，利用大数据推动教育决策由粗放型向精细化、智能化的方向发展。