基于PSO 算法优化模糊PID 的BLDCM 仿真研究

史麦瑞，隋雨伯，王晨宇，朱梓源，芶静文

（辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125000）

0 引言

无刷直流电机（ brushless direct current motor，BLDCM），不但具备交流电机结构简单、维护方便等优点，在工作时，也具有功率密度高、转矩电流比大、不产生逆向火花、调速性能好等优点，被广泛应用在工业控制、家用电器等领域中［1］。传统的PID 控制器虽然其方法成熟简单，有着较高的实用性，但其自适应能力较差，其整体优化功能有待改善［2－3］。本文通过粒子群算法优化模糊控制器的3 个参数以提高直流电机整体的鲁棒性，克服环境因素对其参数追踪的影响，使其控制精度和系统的调速性能得到一定提升，获得更优越的抗干扰能力。

1 BLDCM 工作原理

BLDCM 通常由一个旋转部分（转子）和一个固定部分（定子）组成。定子上有多个线圈，这些线圈通过电子控制器依次通电，电子控制器根据传感器或霍尔效应传感器的反馈，确定转子的位置和速度，产生磁场。定子中变化的磁场使得转子磁极收到吸引和排斥力产生转动力矩，使电机转动。图1 为无刷直流电机原理图。

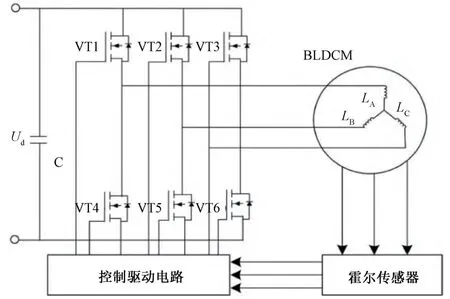
图1 无刷直流电机原理

2 BLDCM 的数学模型及传递函数

2.1 BLDCM 的数学模型

在建立无刷直流电机模型的时候，为了便于分析，忽略一些环境干扰，假定［4］：

（1）磁路不饱和，忽略涡流与磁滞损耗；

（2）三相绕组完全对称，定子电流、转子磁场的分布皆对称；

（3）忽略定子电流的电枢反应，假定电路器件具有理想的开关特性。

此时可用理想电路对无刷直流电机进行分析建模。

在上述条件下建立的电压方程式：

无刷直流电机的电磁扭矩方程和运动方程为：

当绕组为星形联结时方程式如下：

结合电压方程和转矩方程可得出运动方程：

2.2 BLDCM 的传递函数

不考虑暂态换向过程，假设A、B 两相绕组导通时方程式如下：

将式（4）带入式（5）可得电机空载时的电枢电流：

将式（7）带入式（6）整理得出：

对式（8）进行拉普拉斯变换可得无刷直流电机传递函数为：

本文选用的无刷直流电机型号为YZ-57BLS140，参数见表1。

表1 电机参数

将表1 中的参数带入式（9）可得电机的传递函数为：

3 PSO 算法

PSO 算法是根据鸟类捕食行为带来启发而提出的控制优化算法［5］，将每个搜索空间中的鸟看作有着适应值的粒子，粒子追随当前空间的最优粒子移动，在空间飞行的轨迹可看作个体搜索的过程［6］。

标准算法公式为：

式（11）、式（12）中，ω称为惯性因子；vk是粒子的速度矢量；xk是当前粒子位置；pbestk表示粒子目前寻得的最优解的位置；gbestk表示整个种群目前找到的最优解的位置；c1和c2称为学习因子，用于调整pbestk和gbestk对粒子吸引的影响强度［7－8］。图2 为粒子群算法流程图。

图2 粒子群算法流程

4 模糊控制器设计与仿真

4.1 模糊控制器设计

（1）建立PID 参数与误差e和误差变化率ec之间的模糊规则。

（2）控制器的输入量为e和ec， 输入模糊控制器经Ke、Kec的调整转化为输入E、EC。

（3）e和ec输入粒子群寻优器进行迭代寻优，输出优化后的新组合ke、kec、ku。

（4）选择三对称隶属度函数，编辑输入输出变量和模糊规则并将其输出至状态空间。

图3 是基于PSO 优化的自适应模糊控制器结构。

图3 基于PSO 优化的自适应模糊控制器结构

4.2 控制系统仿真

将已经设置好的模糊控制器与经典PID 模型相连，在模糊控制器前加入限幅，将输入的阶跃信号限制在饱和上下限之间。搭建PID、模糊PID 以及PSO 模糊PID 仿真模型并合并为一个输出显示，将粒子群算法写入Matlab Workspace 中，进行迭代寻优，将得出的ke、kec、ku的值代入如图4 所示的仿真模型当中，即可得到三种控制方式下的电机转速响应曲线，见图5。

图4 PSO 模糊PID 结构图

图5 三种模型响应曲线

由曲线可得出：通过粒子群迭代寻优以优化模糊PID的参数组合，明显优于其他两种控制方式，所得曲线在超调量、响应时间以及稳态误差方面都有着明显的减小，对直流电机来说有着更小的转速超调与转速波动，使其快速进入稳定运行状态，提高其安全性并获得更好的稳定性。

5 结语

本文首先建立了传统PID 与模糊PID 模型并对他们进行建模仿真，再通过粒子群算法对模糊PID 控制器的参数进行迭代优化，得到优于传统PID 和模糊PID 的参数组合，通过仿真实验验证得出：基于PSO 优化的模糊PID 控制器在控制直流无刷电机上有着更好的控制效果，模型有效性与可行性得以验证。

本文提出的模型虽能够起到优化的效果，但由于迭代次数受限以及粒子群算法本身的局限性与算法效力问题，优化模型算法部分仍有着较大的改进空间。由于PSO 算法优化属于离线优化，因此对参数变化的鲁棒性还需要更深层次的研究，也是未来研究的重要方向。