基于分布式智能监测装置的配电网低压电缆故障定位方法

王国鸿 宁 楠 蔡宇宁 陶 钢 何先奎

（贵州电网公司贵安供电局）

0 引言

目前，配电网低压线路常用电缆进行电能的传输，而电缆线路因其所处环境、面临的人为因素等，使电缆易发生绝缘破损、断线等故障，严重将引起恶性事件[1-3]。因此，快速判断电缆故障类型与实现故障精准定位，对降低电缆故障带来的运行风险、提高供电可靠性、预防事故发生具有重要作用。

而随着新型电力系统的发展[4-5]，新型智能装置的应用得到快速发展。智能装置具备功能可扩展、软硬件分离、多端通信等特点，可针对不同场景设计出具有较优性能的应用软件[6-8]。且智能分布式监测装置彼此通信，在满足本地数据的处理之外，可作为相邻智能装置的后备资源，分布式协同方式使任务处理更具灵活性。

如今，关于电缆故障定位的研究，文献[9-10]阐述了当前电缆的故障原因包括绝缘故障、超负荷故障、短路故障、闪络故障等。文献[11]提出一种中压电缆的电缆在线监测装置的研制方法，该方法对基于智能装置的分布式监测系统具有启发作用。针对智能装置在电缆监测的研究，文献[12]提出利用边缘计算对电缆的运行状态监测分析，启发智能装置在电缆监测中的应用。文献[13-14]提出一种利用智能装置的分布式任务协同处理架构与方法，为本文的监测装置协同、跨区域节点连接情况识别提供借鉴作用。

因此，本文提出一种利用智能监测装置的电缆分布式监测系统的故障定位方法。首先阐述智能监测装置架构，以及由监测装置构建的分布式监测系统；其次，提出了分布式监测系统架构下的监测节点关联关系分析方法，该方法既实现监测装置的跨区域节点连接情况识别，又可用于本地节点连接变化情况。再次，提出基于节点关系矩阵的电缆故障定位方法，该方法有效求解了电缆故障类型与故障位置。最后，算例验证了本文所提方法的适用性，具有较高工程应用价值。

1 分布式监测装置协同架构

1.1 分布式监测装置构成

如图1所示为面向配电网低压交流电力电缆泄漏电流的监测装置的构成图，其主要由三个层面组成：一是功能层，根据监测装置的应用场景进行相应功能的配置，包括高精度数据同步合成、监测数据曲线查看、输出月/年度运行报告、共零回路灵活配置、故障录波在线读取、联动跳闸控制、采集方案灵活选择、固有漏电补偿、CT断线短线监测；二是操作系统层，其主要实现对硬件资源的管理，包括容器管理、资源虚拟化、镜像构建、容器引擎、进程管理等[15-16]；三是通信层，通信层主要实现了对被监测点数据的采集、监测数据的上传以及与其他装置的通信等。

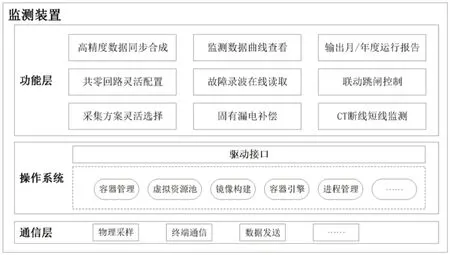
图1 监测装置架构图

1.2 纵向协同

利用智能监测装置对电缆各种信息进行监测，且智能监测装置一般可采集监测多个节点，即监测装置与采集点呈现一对多关系，在通信上形成了不同层级的节点间的关联关系，如图2中一台监测装置管理一个虚线框中的节点，本文将其称之为纵向协同。根据电缆节点的地理分布、节点的通信条件差异，不同监测装置管辖范围内的节点数量有所不同，且不同监测装置的管辖区域存在一定的重叠区域。

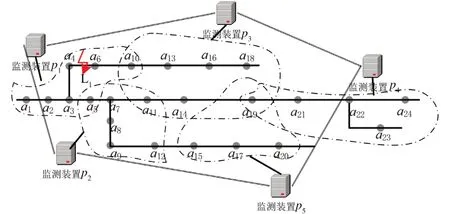
图2 基于监测装置的分布式监测系统架构

进一步地，本文刻画了纵向协同中各个节点间关联关系如下：

式中，ai为监测节点，i∈N+；p为监测装置编号；若装置p监测节点ai，则f（p，ai）=1，反之f（p，ai）=0。

1.3 横向协同

在如图2所示的分布式监测系统中，监测装置除监管本地电缆节点之外，还与相邻的监测装置进行通信[17]，如图中的双实线所示。此外，电缆节点间也存在相互关联关系。因此，本文提出横向协同对上述属于同一层级节点的关联关系进行刻画。在横向协同中，利用变量cij刻画节点ai与节点aj的关联关系，如下所述：若节点ai、aj间存在直接相连的关系，则cij=1，否则cij=0。

2 监测节点关系矩阵及其复杂度计算

2.1 监测节点关系矩阵

本文在1.2节中利用f（p，ai）描述了监测装置p与监测节点ai间的关系，当确定所有满足f（p，ai）=1的i即可确定监测装置p所监测的节点。在1.3节中对监测节点间的关系进行了相关描述，进一步地，本文将cij所构成的矩阵C称为监测节点关系矩阵，基于纵向协同架构与横向协同，关系矩阵又可根据监测装置的不同划分为若干子矩阵，如Cp1、Cp2等，用下标p1、p2表示监测装置p1与p2。节点关系矩阵如下所示：

在图2所示的架构图中，相邻两台监测装置所管控的区域存在一定的重叠区域，即重叠区域内的节点ai同时满足f（p1，ai）=1、f（p2，ai）=1。横向协同架构中相邻的监测装置彼此进行数据交互，本地的节点关系矩阵中阐述了包含重叠区域节点的各节点间的关联关系，故在获取相邻监测装置的节点关系矩阵后，本地监测装置即实现了对跨区域的节点连接关系的获取，即重叠区域内的节点联系了相邻的两台监测装置。

2.2 监测节点关联关系分析

节点关系矩阵直观阐述了监测节点的相连关系，为了使监测装置更好地掌控本区域、跨区域节点的关联关系，本节基于节点关系矩阵进一步分析了各监测节点的关联关系。

首先，本文定了节点间的层级关联以描述不同节点之间的联系，层级关联包括一级关联、二级关联等。其中，一级关联表示监测节点在电缆线路上是直接相连的；二级关联表示两个电缆监测节点ai、aj之间无线路上的直接连接关系，但这两者均与第三个节点ak存在一级关联，则节点ai、aj之间存在二级关联；以此类推，若两个节点存在（n+1）级关联，则说明这两个节点需要经过n个节点构成关联。

对于监测节点的层级关联，本文提出利用如下方法进行计算得到。对节点关系矩阵C进行n次Boolean矩阵运算即可得到两个节点的（n+1）级关系矩阵C（n），以上标（n）表示n级关联。矩阵C（n+1）中的每个元素通过式（3）～式（5）确定，若C（n）

ij=0且C（n+1）ij=1，则说明节点ai、aj之间存在n级关联。对节点关系矩阵C的进行多次的Boolean矩阵运算，实际是在动态计算中确定监测节点处于与参考节点间的层级关联，即：

式中，m为电缆监测系统中总的监测节点数量；式（3）表示矩阵C（n+1）中各元素的计算方法，以C（n+1）ij为例，其由C（n）ij的第i行中的元素依次与C的第j列中的元素进行Boolean逻辑运算，当第i行、第j列中同时存在元素为1时，则该Boolean逻辑运算的值结果为1，矩阵C（n+1）ij中的对应元素将被赋值为1。

2.3 关系矩阵复杂度计算

通过节点关系矩阵分析电缆节点间的关联关系，该过程的计算复杂度随Boolean矩阵运算次数的增加而增加[18]，本文对节点关系矩阵的生成过程的计算复杂度分析如下。

节点关系矩阵C由若干子矩阵组成，且各子矩阵存在一定的关联关系，因此对子矩阵进行复杂度即可完成对矩阵C的分析，本节以子矩阵Cp1与Cp2进行复杂度的分析。首先，生成矩阵C（n）p1时进行的逻辑运算次数与监测装置p1管控区域具有的节点数量有关，当有x（p1）个节点时，矩阵C（n）p1的复杂度如式（6）所示：

式中，Q（p1）为生成矩阵C（n）p1的复杂度，同理可计算矩阵C（n）p2的复杂度Q（p2）。

另外，在横向协同架构中，监测装置p1与p2通过节点a3进行跨区域节点的识别，则在本地监测装置p1获取相邻监测装置p2的节点关系矩阵后，p1进一步综合本地节点与跨区域节点的关联关系，则监测装置p1的复杂度变为：

所以矩阵C的复杂度为：

3 基于节点关系矩阵的故障定位方法

低压电缆的常见故障包含了短路、断路等，故障发生的位置可分为监测节点所在位置故障、两个节点中间的线路位置故障。对于监测装置而言，短路或断路故障在两个相邻监测节点间将呈现一定的差异，以相邻节点的关联关系进行体现。

当电缆线路发生接地短路故障时，故障点与地的电气距离将缩小至零，若故障发生于监测节点ai，则在节点关系矩阵中与ai具有一级关联、但彼此为二级关联的若干节点，将转变为一级关联，则在计算关系矩阵复杂度过程中，若有层级关联关系发生改变的节点，即可判断其具备一级关联的共同节点发生短路故障。若故障发生于两个监测节点ai、aj间的线路，则节点关系矩阵中将新增一个接地节点，故节点ai、aj将从一级关联变为二级关联，其他节点与ai、aj的层级关联也将发生相应变化。

当电缆线路发生断线故障时，该故障一般发生于两个监测节点的中间位置，由于在纵向协同架构下发生断线故障区域的节点数量不发生变化，故子矩阵的关系矩阵复杂度不发生变化。监测装置对该故障的反应将体现于节点关系矩阵的前后两次计算中发生较大变动，如使断线位置的两个节点从一级关联关系变为该区域下的最大层级关联。

基于节点关系矩阵的电缆监测系统故障定位方法如图3所示。

图3 分布式监测系统故障定位方法

4 算例分析

以如图2所示的电缆系统的拓扑结构为例，系统内共包含24个节点，由5台监测装置构成分布式监测系统，每台智能监测装置的监测节点如图1所示，则x（p1）=7、x（p2）=6、x（p3）=7、x（p4）=5、x（p5）=4。

以纵向协同架构中装置p1的管控范围为例，各节点的关系矩阵Cp1、以及层级关联计算过程中的矩阵C（4）

p1如下所示：

监测装置p1在进行4次Boolean矩阵运算后的结果如C（4）p1所示，当再进行一次Boolean矩阵运算后监测装置p1的节点关联矩阵C（5）p1变为单位矩阵。

当在如图2所示的电缆监测系统中的L1位置发生短路故障、断线故障时，监测装置p1管控范围下的节点关系矩阵变化为：

矩阵Cp1在故障前后的复杂度如下表所示，由表可知计算节点关系矩阵的复杂度为仅进行不超过2000次的逻辑运算，对于智能监测装置而言可以快速求解出节点关系矩阵。

表 故障前后Cp1的复杂度变化情况

所以基于图3所示的分布式监测系统故障定位方法，当监测装置识别、计算出节点关系矩阵的复杂度、层级关联关系发生变化时，根据变化情况可以快速准确定位故障的类型与故障位置。

若复杂度发生变化，则说明该系统发生故障，根据节点关系矩阵变化情况，计算得Cp1短，比较Cp1短与Cp1得到节点a4和a6从一级关联关系变为二级关联关系，a4和a10从二级关联关系变为三级关联关系，a5与a6从二级关系变为三级关系，所以判断出短路故障位于节点a4和a6之间的电缆线路上。同理，若节点关系矩阵复杂度未变，需进一步判断节点关联关系的变化情况，通过计算节点关联关系矩阵得到Cp1断，比较Cp1断与Cp1，可以发现节点a4与a6从一级关联变为没有关联，a4与a10从二级关联变为没有关联。a5和a6从二级关联变为没有关联，则说明为断路故障，且故障位于节点a4与a6之间的线路上。同理，可以用相同的方法分析其他区域内的故障定位。

5 结束语

针对电缆易发的故障如短路、断路故障，本文提出一种基于智能监测装置的分布式监测系统的故障定位方法。智能监测装置通过管控多个监测节点，并与相邻的监测装置进行数据交互，通过重叠区域内的节点分析跨区域的节点连接情况，并利用节点关系矩阵的复杂度、节点层级关联关系的变化情况，可快速判断电缆的故障类型与故障位置，为实际工程应用解决电缆故障问题提供了有效手段。