基于外力矩观测器的机器人碰撞检测

张铁 陈亿杰 邹焱飚

（华南理工大学 机械与汽车工程学院，广东 广州 510460）

当工业机器人在工作环境中与人类共享同一空间时，可能会导致意外的碰撞而伤害人类，为了降低这种风险，需要有一种可以检测碰撞的方法。目前，对工业机器人的碰撞检测通常分为基于外部传感器的碰撞检测和免传感器的碰撞检测两种方法。

基于外部传感器的碰撞检测，主要是在机器人结构上安装额外的传感器，通过传感器的实时反馈并结合控制系统实现碰撞检测，例如，Flacco等［1］在工作环境中加装视觉传感器检测人机距离实现碰撞检测；Li等［2］在用于固定机器人的底座处安装力/力矩传感器并结合机器人动力学模型实现碰撞检测。然而，上述方法存在以下两方面的问题：一方面，额外传感器数据的采集和处理可能会增加控制系统的复杂性；另一方面，为保证工业机器人关节的高刚度，通常没有配备安装外部传感器的结构，且高性能传感器的成本普遍较高，安装额外的传感器会增加工业机器人机械结构的复杂性和硬件成本。

为解决上述问题，免传感器实现碰撞检测得到了高度关注，主要分为两种实现方式：第一种是使用智能算法直接区分碰撞信号和非碰撞信号。例如，Park等［3］提出了基于监督学习的检测方法，使用支持向量机和卷积神经网络对硬碰撞和软碰撞分别进行特征提取，用四维和六维时间序列数据堆栈训练的六关节机器人实现碰撞检测。Park等［4］提出了基于无监督异常检测算法的碰撞检测方法，仅使用无碰撞运动下的数据训练模型即可鲁棒地检测各种类型的碰撞。上述方法虽然可以准确识别碰撞信号，实现碰撞检测，但是往往需要大量的数据进行离线训练，且智能算法的复杂性可能会降低碰撞检测实时性。

另一种实现方式是根据机器人的动力学模型和运动状态来估计外力矩值，设置置信阈值并假定高于阈值的部分是由碰撞引起的［5］。Haddadin等［6］对该方式实现碰撞检测的整体流程进行了拆分并做了全面概述，将实现过程分为关节外部力矩估计和碰撞识别两个环节。其中关节外部力矩估计的准确性是影响碰撞检测精度的主要因素。Zhang等［7］分别建立机器人关节和电机的动力学方程，用两者计算的差值来估计外力矩，但该方法获得准确的估计精度需要建立复杂的摩擦力模型。文献［8-10］中通过引入广义动量将动力学模型转化成不含加速度的形式，减少噪声的干扰，进而将广义动量的残差量作为观测量，构建一阶外力观测器，实现了对关节外力矩的迭代估计。Han等［11］基于模型辨识方法建立高阶有限时间观测器来估计外部时变相互作用力。上述建立观测器的方法没有考虑到动力学模型的辨识误差等影响。在碰撞识别过程中，当外部力矩估计准确时，设置静态对称置信阈值［12-14］即可实现碰撞识别。然而，外力矩估计模型并不能保证完全准确，采用静态对称阈值的方法会产生误报。文献［15-16］中根据外力矩估计值生成动态阈值，具有更好的检测准确性和鲁棒性。

针对动力学模型辨识误差和电机电流测量误差导致的外力矩估计不准确以及静态对称阈值可能产生误报的问题，本文提出了一种基于扰动卡尔曼滤波外力矩观测器的碰撞检测方法。该方法分为3个步骤。第1步基于扰动原理定义机器人的关节扰动模型，以机器人广义动量和扰动动力学变量为状态变量，并结合动力学模型转化为状态空间方程。第2步考虑动力学的模型辨识误差以及电机电流测量过程中引入的噪声，基于卡尔曼滤波算法进行迭代估计得到最优外力矩观测值。最后，提出一种随关节速度变化的时变对称阈值函数，根据外力矩观测器的输出值来实现碰撞检测，以提高碰撞检测的灵敏度。

1 机器人关节受力分析

如图1所示，在具有垂直关节的n自由度串联型机器人的运动过程中，若机器人关节发生碰撞，则第i关节所受到的力/力矩包括摩擦力τf，i、关节运动克服自身重力、惯性力等所需力矩τd，i、电机实际的驱动力矩τm，i以及碰撞力等效的力矩τext，i。此时，机器人动力学平衡方程可以表示为

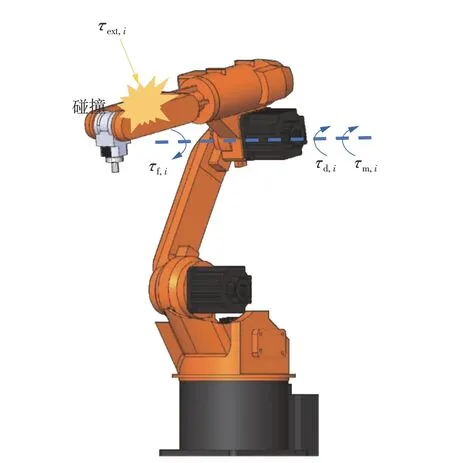
图1 机器人运动过程中的力/力矩分析Fig.1 Force/torque analysis during robot movement

式中：τf∈Rn×1表示各关节受到的摩擦力矩矢量；τd∈Rn×1表示各关节运动克服自身重力、惯性力等所需的力矩矢量；τm∈Rn×1表示各关节的电机驱动力矩矢量；τext∈Rn×1表示碰撞外力等效至各关节的外力矩矢量。关节完成目标运动所需力矩τd可以等价为

式中：M(q)∈Rn×n表示惯性矩阵；C(q，)∈Rn×n表示科里奥利和离心力矩阵；G(q)∈Rn×1表示重力矢量；q、、分别表示关节转角、关节速度和关节加速度。

为了实现碰撞检测，需要能够实时计算碰撞力等效的力矩值τext，由式（1）可以得到碰撞力等效的力矩计算公式为

由上式可知，计算碰撞力等效的力矩需要知道机器人的关节摩擦力、动力学参数以及机器人运动过程中的关节转角、关节速度、关节加速度和关节驱动力矩。由于关节摩擦力在高速运动过程中与关节速度之间表现出了近似的线性关系，所以摩擦力模型通常采用库伦摩擦与粘性摩擦相结合的线性方程描述，即：

式中，fc，i为关节i的库伦摩擦系数，fv，i为关节i的粘性摩擦系数，S(·)为符号函数。

2 机器人免传感器碰撞检测方法

2.1 机器人动力学模型的状态空间表达式

在得到机器人的动力学参数后，可以根据式（3）实时计算碰撞力的等效力矩τext。然而，工业机器人通常不配备加速度̈的信号采集器，无法直接获得̈信号。常用的̈信号获取方法是对速度q̇信号进行差分计算，但是这样会放大信号采集过程中的噪声，从而导致外力矩估计不准确。为解决上述问题，引入机器人的广义动量p，具体表达式为

根据机器人动力学的结构可知惯性矩阵M(q)是对称矩阵，为斜对称矩阵［8］，可以得到：

结合式（3）、（5）、（6），则在运动过程中受碰撞时的机器人动力学方程式可表示为

在动力学参数辨识过程中，由于动力学的非线性特性以及摩擦模型不准确，导致参数辨识结果存在偏差。考虑动力学参数辨识的误差，则上式可进一步表示为

机器人与环境发生碰撞产生的外力可以看作机器人系统自由运动时的扰动。由于碰撞力等效的力矩τext是由外界系统产生的，根据扰动原理［18］，关节扰动模型可描述为

式中：ωτ∈Rn×1表示扰动动力学变量；S∈Rn×n和H∈Rn×n表示扰动的系统矩阵；ed～N(0，Σd)表示扰动模型的误差项，定义为高斯噪声，其中Σd∈Rn×n表示ed的协方差对角矩阵。

结合式（8）-（9），将扰动动力学变量与机器人广义动量组合为状态变量，并定义机器人广义动量为状态空间的输出，建立机器人外力矩观测系统，其状态空间方程表示为

式中，系统状态x=[pn×1ωτ，n×1]T，系统输入u=τu，n×1，系统状态转移矩阵A、系统输入矩阵B与系统输出矩阵C分别为

式中，In×n为n×n维的单位矩阵。系统的过程噪声w表示为w=[eTpeTd]T，即：

由于机器人的关节转角和关节速度是可测量的，所以系统的输出定义为可测量的动量，即y=p，测量噪声v定义为高斯噪声v～N(0，Σo)，其包括测量关节转角以及关节速度时引入的噪声，其中Σo∈Rn×n表示测量噪声v的协方差对角矩阵。

2.2 基于卡尔曼滤波的外力矩观测器

为了得到式（10）的最优状态，从而得到关节外力矩的最优观测值，采用卡尔曼滤波算法［19］进行最优状态估计。因为卡尔曼滤波是一个递推型算法，所以对式（10）进行离散化处理，即：

式中，k为离散系统的时间变量。离散后的系统矩阵Ak，Bk可通过计算系统矩阵的矩阵指数［20］获得：

式中，Ts为机器人系统的采样周期，exp(·)为矩阵指数运算的算子。

由于系统的输出没有随时间发生变化，输出矩阵Ck保持不变，测量噪声vk的协方差矩阵Rk只与采样周期Ts相关，则：

过程噪声wk的协方差对角矩阵Qk通过如下的矩阵指数运算得到：

在k时刻，使用卡尔曼滤波算法得到最优系统状态xk后，则该时刻的机器人关节外力矩估计值矢量为

对于离散后的系统状态方程式（10），采用卡尔曼滤波进行最优状态估计获得关节外力矩的过程可概括为如下算法

基于卡尔曼滤波的关节外力矩估计算法1 初始化系统状态和状态协方差矩阵：x0=0(n+n)×1， P0=In×n；2 在离散系统的每一个采样周期下（k≥1）；3 根据关节转角q(k)与速度q̇(k)的测量值，更新系统输出yk=pk=M(q(k))q̇(k)；4 采集电机驱动力矩τm(k)的测量值，更新系统输入uk=τu(k)；5 根据式（12）-（14）计算系统矩阵与协方差矩阵Ak，Bk，Ck，Rk，Qk；6 预测系统状态和状态协方差矩阵：x̂k=Akxk-1+Bkuk，P̂k=AkPk-1Ak T+Qk；7 更新卡尔曼增益：Kk=P̂kCk T(CkP̂kCk T+Rk)-1；8 使用系统输出校正系统状态和状态协方差矩阵：xk=x̂k+Kk(yk-Ckx̂k)，Pk=(I-KkCk)P̂k；9 根据最优的系统状态对关节外力矩进行观测：τ̂ext(k)=()[]0n×nH·xk；10 停止观测。

2.3 基于外力矩观测器的碰撞检测

对于工业机器人关节i，在得到观测器输出的力矩估计值τext，i后，令其阈值函数为Ri(x)，然后对力矩估计值进行实时判断。当力矩估计值超出阈值范围时，则认为超出的部分是由外界碰撞导致的。因此，定义检测信号Ti来判断机器人关节是否发生了碰撞，即：

式中，Ti(k)为关节i在k时刻的碰撞检测信号，τext，i(k)为关节i在k时刻外力矩观测器的输出信号，Ri(k)为关节i在k时刻阈值函数的输出值。Ti(k)=1，表示关节i在第k时刻发生碰撞；Ti(k)=0，表示关节i在k时刻无碰撞发生。

在实际运动过程中，外力矩观测器输出值可能会受到以下因素的影响：（1）电流测量噪声 由于机器人本身没有力矩传感器，关节驱动力矩是由关节电机电流转换得到的，在采集电流过程中可能存在噪声；（2）摩擦力误差 由于目前还没有准确的摩擦模型能准确拟合实际的摩擦现象，采用的摩擦模型只能近似拟合摩擦力，所以计算摩擦力与实际摩擦力存在误差。

由于上述误差的存在，即使机械臂未发生碰撞，外力矩观测器的输出信号τ̂ext，i也可能不为0。所以根据实际情况提出适用于外力矩观测器的置信阈值函数可以提高检测鲁棒性。上述的误差因素中，摩擦力误差对外力矩估计的准确性影响较大。所用的摩擦模型在中高速运动时对摩擦力有较好的拟合效果而低速时的拟合效果不足，导致外力矩观测器的输出在低速运动时会出现较大的偏差。综合上述分析，提出一种同关节速度变化的阈值模型，该模型可以描述为

式中，C为阈值常数，β为随速度衰减系数，当关节运动速度较小时表现出较大的阈值，当关节运动速度较大时表现出较小的阈值，Δfv为粘滞摩擦系数误差量，Δfc为库伦摩擦系数误差量。时变阈值模型的参数根据实际实验结果进行优化。

3 机器人外力估计和碰撞检测实验

3.1 实验平台与系统

为了验证所提外力矩观测器的性能以及碰撞检测方法的准确性，本文基于GSK-RB08A3型工业机器人实验平台进行实验验证。机器人系统结构如图2所示。平台采用EtherCat总线协议进行通信，使用装载Kithara实时控制系统的工控机作为上位机进行实时交互。在运动过程中，机器人关节转角以及电机电流信号由机器人本体的编码器采样得到，通过机器人控制柜发送到上位机，并显示在实时控制系统的交互界面。上位机根据反馈信号计算控制指令，通过机器人控制柜产生驱动信号控制机器人运动。机器人系统的控制和通信周期为1 ms。

图2 机器人系统Fig.2 Robot system

3.2 动力学模型参数辨识验证

计算外力矩观测器的输出信号需要机器人连杆的动力学参数，在无碰撞条件下进行参数辨识实验。首先，使用SymPyBotics工具箱［21］建立机器人刚体动力学模型，并得到最小可辨识参数集，然后采用具有周期性的有限傅里叶级数［22］作为激励轨迹驱动机器人跟踪轨迹采集关节转角信号和力矩信号，使用三阶巴特沃斯低通滤波器对采样信号进行滤波。最后基于最小二乘法对刚体动力学参数进行辨识。参数辨识流程具体可参照文献［23］。

图3表示机器人前3个关节辨识出的动力学模型参数在激励轨迹上的性能。其中黑色曲线表示跟踪激励轨迹过程中采集的实际测量扭矩，红色曲线表示通过动力学模型计算的力矩值，蓝色曲线表示测量力矩与模型计算力矩之间的误差，绿色曲线表示关节运动速度曲线。利用整体辨识方法得到的动力学参数，前3个关节的整体力矩预测均方根误差值分别为2.4、15.3和6.2 N·m。从图中可以看出，在运动平稳时，即关节速度的绝对值大于0.05 rad/s时，能够较好地预测关节力矩，此时前3个关节的预测均方根误差值分别为0.4、4.5和1.6 N·m；然而在速度换向处，即关节速度的绝对值小于等于0.05 rad/s时，会出现较大的偏差，此时前3个关节的预测均方根误差值分别为15、158和55 N·m。

图3 参数辨识验证Fig.3 Parameter identification verification

3.3 外力矩估计方法实验验证

为验证所提外力矩观测器的准确性和有效性，使用与参数辨识相同的激励轨迹进行仿真评估。应用提出的扰动卡尔曼滤波观测器估计外力矩值，并与文献［8］中的广义动量观测器的性能进行对比。为了使所提外力观测器具有较优的性能，本文通过仿真实验反复进行调整，协方差矩阵参数设置为对角矩阵且均为常数，具体参数值如表1所示。广义动量观测器的增益矩阵设置为Ko=diag(20，20，20，20，20，20)。

表1 扰动卡尔曼滤波观测器中协方差矩阵参数Table 1 Parameters of covariance matrix in disturbance Kalman filter observer

以关节1和关节4为例分析外力矩观测器的性能。图4表示无碰撞时两种不同观测器的输出值对比曲线图。图中蓝色曲线表示广义动量观测器的输出值，红色曲线表示扰动卡尔曼滤波观测器的输出值，黑色曲线表示关节速度。

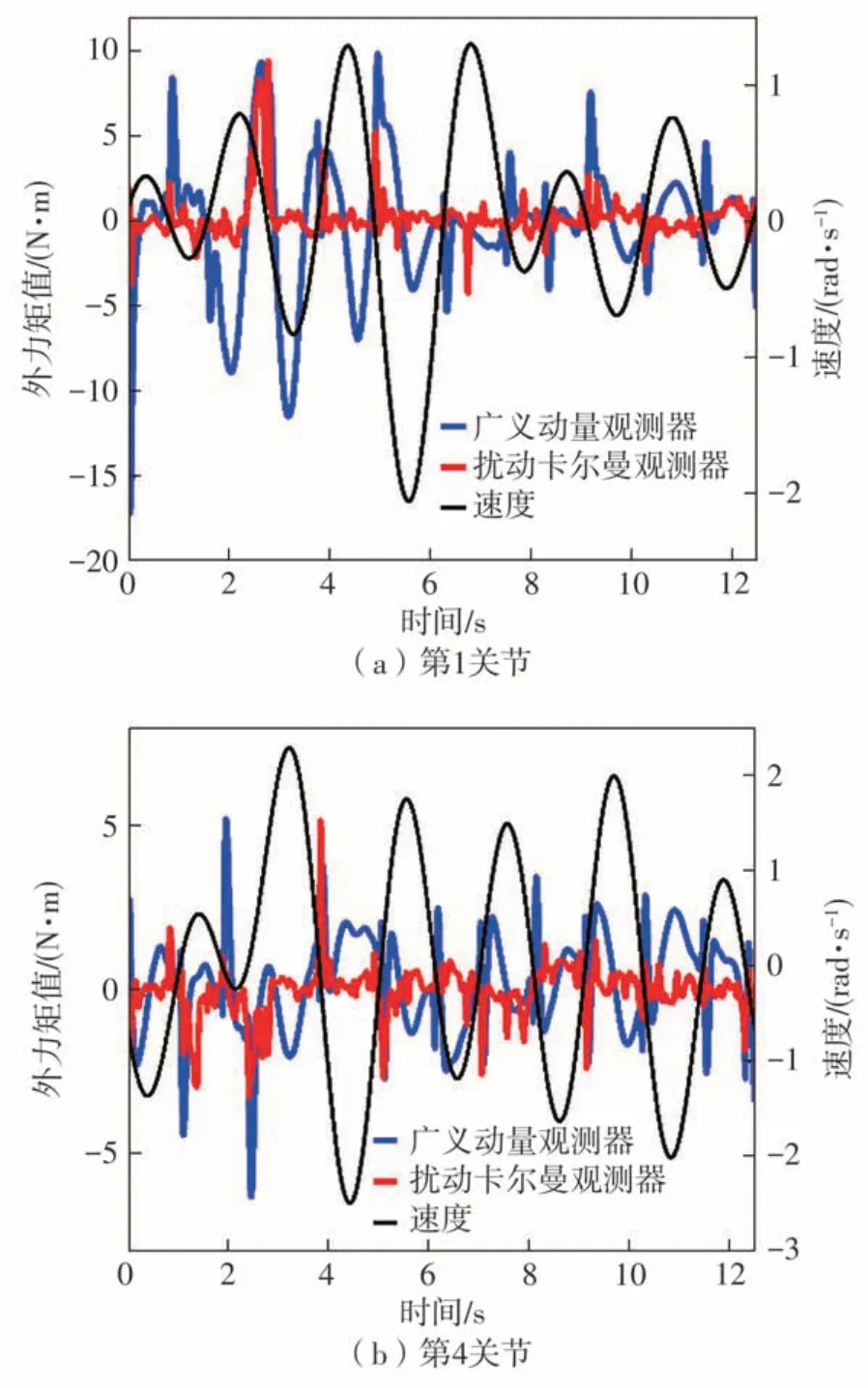
图4 无碰撞下的外力矩观测器输出对比Fig.4 Comparison of the output of the external torque observer without collision

从图中可以看出，与广义动量观测器的输出值相比，扰动卡尔曼滤波观测器的输出值关节1的平均输出误差值减小了2.46 N·m，精度提高了65.56%，关节4的平均输出误差值减小了0.75 N·m，精度提高了50.14%，说明在无碰撞情况下，所提观测器的精度优于广义动量观测器。然而，在关节速度发生变化的过程中，两种观测器的估计误差都增大，主要的原因是摩擦模型在低速时无法准确拟合摩擦力的真实情况。为了更详细的进行比较，采用均方根误差作为评价指标，量化两种观测器的估计效果。表2表示无碰撞时两种外力矩观测器的输出均方根误差值。表中给出了机器人6个关节的观测器输出均方根误差值，具体的机器人关节图可以参考图2。从表2中可以看出，扰动卡尔曼滤波观测器整体上有更小的均方根误差，力矩估计精度提高了52.03%，说明所提的外力矩观测器具有更高的精度。

表2 无碰撞下的外力矩观测器输出均方根误差值Table 2 Root mean square error of the output of the external torque observer without collision

3.4 免传感器碰撞检测实验

将所提的外力矩观测器用于实时监控关节外力矩变化，以机器人第1关节为例分析碰撞检测方案的有效性。在实验过程中，机器人跟踪直线运动轨迹，做一次往返运动。图5表示用于碰撞检测实验的运动轨迹图，起点位姿P1为［720，-300，640，180°，0，0］终点位姿P4为［525，730，640，180°，0，0］。一次往返运动即从点P1经过P2，P3到达P4，再从P4经过P3，P2回到点P1后停止。

图5 用于碰撞检测实验的仿真轨迹Fig.5 Simulation trajectories for collision detection experiments

为了提高碰撞检测灵敏度，降低碰撞的误报率，本文通过反复对阈值函数的参数进行调整，设置碰撞阈值函数的参数为：C=15，β=25，Δfv=1.57，Δfc=1.01。在实验过程中，为了更好的观测外力矩观测器的输出曲线，在机器人发生碰撞后不中断机器人原有运动，完整运行整个直线运动轨迹。

在实验中，首先让机器人在无碰撞下跟踪直线运动轨迹，得到外力矩观测器的输出值。图6表示无碰撞运动过程中关节1的外力矩观测器输出值与阈值曲线，从图中可以看出，在机器人启动和换向阶段，不准确的摩擦模型以及一些非线性特性会造成观测器输出值发生突变，此时的碰撞阈值也会跟着发生突变，防止发生碰撞误报。

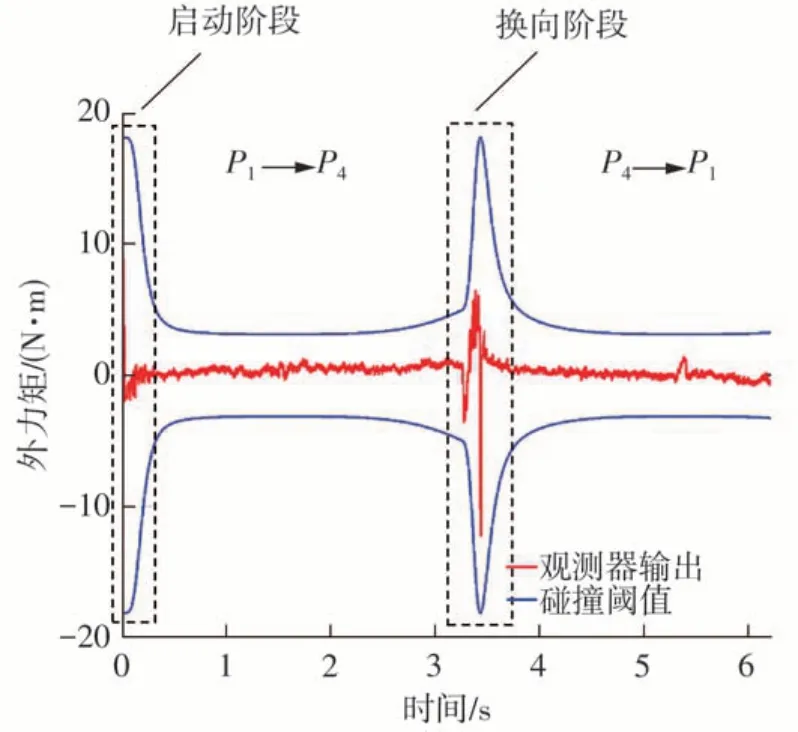
图6 无碰撞下外力矩观测器输出曲线Fig.6 Output curve of external torque observer without collision

在机器人运行过程中，用金属棒敲击机器人关节模拟外部碰撞。模拟碰撞实验过程中，启动系统定时器，以显示机器人系统检测到发生碰撞的时间。图7表示碰撞下关节1的外力矩观测器输出值和阈值曲线。从图中可以看出，在没有发生碰撞的时间段，观测器的输出曲线与无碰撞运动过程中的曲线相似。碰撞实际发生在2 575 ms处，外力矩值约为-3.54 N·m，此时阈值上、下限为［3.41，-3.41］N·m，而此时机器人系统没有检测到碰撞发生，在经过18ms后，即2 593 ms机器人系统发出碰撞警报。为了测试碰撞检测方法的实用性，分别在有无碰撞下重复运行直线轨迹各200次。在无碰撞过程中，机器人发出3次误报，在启动和换向阶段时分别产生2次和1次误报，误报率为1.5%。在有碰撞实验过程中，系统均成功检测到碰撞的发生，包括在关节换向阶段，实际发生碰撞的时间与系统发出警报的时间平均相差约35 ms，即系统的平均延时约为35 ms。

为了进一步分析时变阈值在碰撞检测灵敏度中的作用，分别在碰撞检测中使用静态对称阈值与时变对称阈值进行人机碰撞对比实验。在该实验过程中，机器人检测到碰撞后立即执行急停指令，以展示两种不同阈值函数在实际碰撞情况下的灵敏度。实时外力矩值与阈值曲线如图8所示，图8（a）表示时变对称阈值下的碰撞检测，在1 965 ms左右发生人机碰撞，机器人系统在2 017 ms成功检测并执行急停，检测延迟约52 ms；图8（b）表示静态对称阈值下的碰撞检测，碰撞实际发生在约2 181 ms，机器人在2 305 ms成功检测并执行急停，检测延迟约124 ms；从上述实验对比结果可得，与静态阈值对比，时变阈值下的碰撞检测延时缩短了58.06%，说明了时变阈值函数在碰撞检测的灵敏度更高。

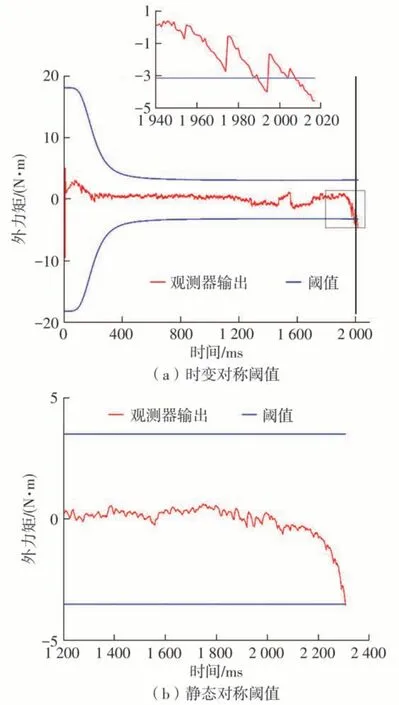
图8 不同阈值函数下的碰撞检测对比Fig.8 Comparison of collision detection under different threshold functions

4 结语

为了降低动力学模型的参数辨识误差以及电机电流的测量误差等因素影响外力矩估计的准确性，提高碰撞检测的精度。本文设计了一种扰动卡尔曼滤波外力矩观测器。该观测器基于扰动原理，将外部碰撞等效的外力矩作为扰动项，定义了关节扰动模型，并引入机器人的广义动量构建状态空间方程式。建立状态空间方程过程中，考虑动力学模型的参数辨识误差以及电机电流的测量误差，并基于卡尔曼滤波算法进行迭代估计，得到最优外力矩观测值，从而实现免传感器的最优外力矩估计。与基于广义动量构建的一阶观测器在无碰撞实验中进行对比，外力矩估计精度提高了52.03%。

为了提高碰撞检测的灵敏度并降低碰撞误报率，本文通过分析可能影响外力矩观测器输出值的因素，提出一种随关节速度变化的时变阈值函数用于检测碰撞，该阈值函数具有更好的鲁棒性。以6自由度串联型关节工业机器人为实验对象，笛卡尔空间直线轨迹为运动轨迹，验证了基于扰动卡尔曼滤波外力矩观测器的碰撞检测方法。实验结果表明，碰撞实验过程中，系统的平均延时约为35 ms，相比于静态对称阈值函数，时变对称阈值函数在检测延迟上缩短了58.06%，提高了碰撞检测的灵敏度。利用该方法进行碰撞检测，无碰撞实验的误报率为1.5%，主要是由于动力学模型的中摩擦模型在启动和换向阶段精度下降导致误报的发生。为了继续降低误报的发生，将在后续工作中对摩擦模型进行进一步研究。