基于延时补偿的新能源惯性时间常数评估方法
朱介北,朱学科,陈彬彬,俞露杰,聂川杰,黄伟煌,郭 铸
(1.天津大学电气自动化与信息工程学院,天津市 300072;2.广西电网有限责任公司,广西壮族自治区南宁市 530023;3.南方电网科学研究院有限责任公司,广东省广州市 510663)
0 引言
风电、光伏等新能源的大规模接入已成为未来电力系统发展的必然趋势[1],但弱/无惯量支撑能力的新能源大规模接入降低了系统惯量。当发生大扰动事件时,系统对频率变化率(rate of change of frequency,RoCoF)的抑制能力变弱,易触发低频减载动作,导致大断电事故风险增加。为解决这一问题,多个国家在并网规程中对新能源惯量响应能力提出了新要求[2-5],并规定了等效惯性时间常数。例如,加拿大魁北克要求风电场提供的惯性时间常数为3.5 s[6];中国规定虚拟同步机的惯性时间常数宜在1.5~6.0 s 范围内[7]。此外,惯性时间常数亦作为重要指标参与市场清算。例如,英国国家电网在惯量服务合同中规定了市场清算须考虑设备的实际惯性时间常数[8];中国南方电网有限责任公司在惯量补偿规则中同样考虑了设备的惯性时间常数大小[9]。
在此背景下,惯量响应的测试评估愈发重要。文献[10-11]规定利用装置模拟爬坡速率为±0.5 Hz/s 的电网频率,对新能源虚拟同步机进行惯量响应测试,并要求响应时间不大于500 ms。不同于利用装置模拟电网侧频率,文献[3]规定的新能源惯量响应测试将不同爬坡速率(±1、±2 Hz/s)的虚拟频率信号直接注入虚拟同步控制器,通过分析输出功率变化情况来实现惯量响应测试。上述文献虽规定了惯量响应测试的方法,但未对用于(并网规程)考核或(辅助服务市场)结算的惯性时间常数这一关键参数进行计算,且未充分考虑RoCoF 的保护限制要求(如英国为0.2 Hz/s、爱尔兰和拉脱维亚为0.4 Hz/s)[12]以及不同故障情况。
在惯量评估方面,文献[13-14]利用系统扰动时的有功功率和频率数据,基于同步机转子运动方程对惯量进行离线评估,但评估效果依赖于扰动发生初始时刻的准确定位。文献[15-16]在此基础上,利用滑动窗口对功率和频率数据进行处理,以提高扰动时刻的定位准确度,但滑动步长和窗长需根据经验手动设定,易对评估结果准确性产生不利影响。文献[17-18]以功率为输入量、频率为输出量,建立了自回归滑动平均模型,通过系统辨识实现惯量评估,但是辨识结果依赖于模型的建模阶次。总体而言,文献[13-18]主要聚焦在扰动发生时刻的惯量计算,而基于时刻的惯量结果无法对测试全过程的惯量响应进行准确表征。但文献[3,10-11]指出惯量响应测试须对测试时段内(而非时刻)对应功率变化进行分析,对其惯量评估亦需要考虑测试全过程,而非采用某一时刻的惯量值。文献[19]从能量角度提出了惯量连续评估方法,但该方法考虑的是扰动后功率与频率变化累积结果之间的关系,扰动后的功率积分结果均会影响当下惯量评估结果,产生误差。文献[20]对受控制回归模型进行辨识并将结果转化为连续传递函数,通过冲击响应结果实现惯量的连续评估,但仍存在模型阶次对结果影响较大的问题。文献[21]通过对转子运动方程进行求导,实现了扰动后新能源惯量的动态评估,但是需要获取准确的并网设备内部等效电抗。为此,需要提出一种适用于新能源惯量响应测试全过程的惯量精确评估方法。
此外,为了提高惯量评估的准确性,文献[14,22]分别以最大RoCoF 的出现时刻和频率波动大于设定阈值时刻作为扰动发生时刻,但该措施难以适用于测试中频率以不同RoCoF 变化的场景。文献[23]指出,惯量响应延时会导致频率和有功功率错位,造成输入、输出的非线性,并通过斜率门槛以及频率功率响应时刻进行延时补偿,但仅进行一次延时估计仍难以消除偶然误差。文献[24]亦考虑了延时因素,并基于系统辨识的方法对微电网中非同步电源的总体惯量进行了估计,但未针对单个新能源惯量测试评估展开研究分析。
为解决惯量响应测试信号RoCoF 单一、缺少适用于测试全过程的惯量评估方法以及延时带来的惯量评估不准确的问题,本文提出了一种基于延时补偿的新能源惯性时间常数评估(delay compensation based renewable energy inertia time constant evaluation,DCIE)方法,其主要特点为:
1)不同于现有测试频率信号的RoCoF 变化单一,所提方法基于最大频率偏差和RoCoF 保护限制对测试频率进行选取,实现不同故障情况可能出现RoCoF 的惯量响应全面评估;
2)所提方法基于测试频率信号,判断测试起止时刻、惯量功率响应起止时刻,对惯量响应延时进行估计并补偿,提高惯量响应性能指标和惯量评估结果的精度;
3)不同于只计算扰动时刻的惯量,本文所提方法利用有功功率和频率信息,基于离散化的同步机转子运动方程进行惯量的连续评估,并以其平均值作为最终结果,适用于多RoCoF 的惯量测试场景。
1 新能源电源惯量响应及评估
1.1 新能源虚拟惯量响应
对同步机而言,惯量通常用来表征其转子固有的旋转质量,可抵抗同步机的机械功率输入与电磁功率输出不平衡所产生的额外转矩。同步机经典摇摆方程可表示为:
式中:Hg和Dg分别为同步机惯性时间常数和阻尼系数;Pm和Pe分别为同步机机械功率和电磁功率标幺值;f为电网实时频率标幺值。
由式(1)可知,同步机的惯性功率ΔPhg为:
新能源虽然不具备真实的转子,但在虚拟惯量控制下可实现虚拟惯性功率输出,表示为:
式 中:ΔPpcc为 并 网 点(point of common coupling,PCC)处的有功功率增量标幺值;Hvset为设定的新能源等效惯性时间常数。
按照能量来源的不同,虚拟惯量控制可以分为以 下3 类:1)最 大 功 率 点 跟 踪(maximum power point tracking,MPPT)模式下,利用风电机组的转子动能[25];2)减载运行模式下,利用风电[26-27]和光伏[28]的备用功率;3)外加储能装置情况下,利用超级电容、电池和飞轮等储能元件[29-31]。MPPT 模式下,利用风电机组的转子动能提供惯量响应存在系统频率二次跌落的风险;长时间减载运行以预留惯量功率会产生弃风弃光现象,经济性差。而通过附加储能元件则可以避免上述问题,鉴于超级电容较电池有更高的瞬时功率输出以及更多的循环充放电次数,更适用于惯量响应,故本文以超级电容作为惯量响应的能量来源。
本文采用的新能源虚拟惯量控制方法[32-34]如附录A 图A1 所示,通过DC/DC 换流器将超级电容接入新能源直流侧,将频率和超级电容电压相关联可实现精准的惯量模拟,且无须对并网逆变器的控制方式进行改动。此外,实际工程中由于存在数据测量、信息传输、指令计算分配、储能响应等环节,新能源惯量控制环节存在延时Tc[23],如图A1 控制回路中的红框所示。
1.2 新能源惯量响应性能评估指标
由式(3)可知,当RoCoF 不变时,新能源惯量响应功率应为一个与Hvset相关的定值。根据这一特点,惯量响应测试通过模拟特定RoCoF 的频率信号和PCC 处的有功功率数据进行分析(亦可采用相关机构确认的新能源模型进行仿真检测,但准确性有所降低)。据中国行业标准要求[10-11],惯量响应测试电路如图1(a)所示,新能源功率输出范围分为大功率(0.7~0.9 p.u.)和小功率(0.3~0.4 p.u.),模拟惯性时间常数范围为2~6 s,数据采集装置位于变压器高压侧。
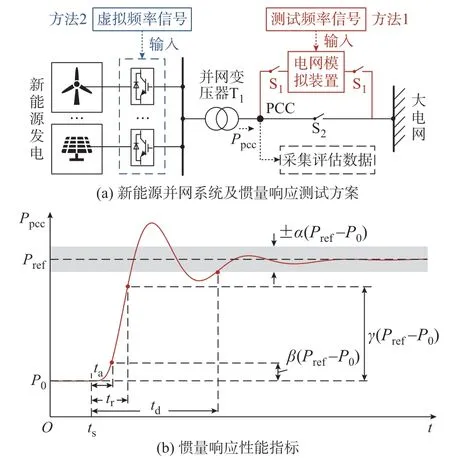
图1 新能源惯量响应评估系统及性能指标Fig.1 Inertia response evaluation system and performance indicators for renewable energy
测试频率信号的模拟方式有两种:1)闭合开关S1、断开开关S2,通过电网模拟器改变PCC 处的实际物理频率,如图1(a)中红线部分所示;2)输入虚拟惯量控制系统中,PCC 的物理频率并未发生改变,如图1(a)中蓝线部分所示。本文采用中国行业标准[10-11]规定的方式1)进行研究,标准给出了惯量响应的性能指标,如图1(b)所示,具体定义如下:
动作时间ta:从设定频率变化开始时刻ts至PCC处有功功率Ppcc达到β(Pref-P0)所需的时间,其中,P0为新能源正常运行状态输出功率稳态值;Pref为惯量响应的目标功率;β取10%。
响应时间tr:Ppcc达到γ(Pref-P0)所需的时间,应不大于500 ms[7]。本文γ取90%。
调节时间td:Ppcc稳定在允许偏差±α内所需时间,其中,±α为允许偏差范围,本文α取2%。
2 新能源惯性时间常数确定方法
本章所提DCIE 方法的步骤为:1)确定测试频率斜率,模拟扰动时系统可能出现的多种RoCoF;2)数据预处理,剔除测量数据噪声;3)测试起止时刻判据,确定测试实际开始和结束时刻;4)惯量响应延时补偿,去除延时对惯量评估结果影响;5)惯量评估,基于离散化转子运动方程实现新能源等效惯性时间常数评估;6)离群点修正,提高评估结果准确性。
2.1 测试频率斜率信号
为模拟严重故障、小扰动时系统可能存在的RoCoF,使评估结果更为准确,本节对测试信号频率斜率进行规定。
首先,测试频率信号应涵盖严重故障下系统频率可能出现RoCoF 的最大值,该最大值通常以装载在分布式电源的RoCoF 反孤岛保护阈值为约束[12]。本文将测试信号的RoCoF 最大值和最小值分别设定为Rmax、Rmin。根据测试RoCoF 组数N可得测试变化步长ΔR为:
由式(4)可得:
式 中:Rn(n=1,2,…,N)为 测 试 的 第n组RoCoF数值。
其次,考虑电力系统运行时对频率偏移量的要求[35],将测试信号的最大频率量设定为Δfmax,由此可得爬坡测试时间tramp为:
以Rn进行M组上爬坡和下爬坡测试,第m组测试的开始和结束时刻设定为tsn,m、ten,m,则
本文每个Rn分别进行4 组上、下爬坡,即下爬坡(50 Hz 以下)、上爬坡(50 Hz 以下)、上爬坡(50 Hz以上)、下爬坡(50 Hz 以上)。
2.2 数据预处理
以等时间间隔T(本文采样间隔设置为10 ms)对PCC 处的数据进行测量,取第i个采样时刻(t=iT)对应的有功功率和频率分别为P(iT)、f(iT)。由于测量的数据通常会夹杂噪声,通过滤除直流分量、低通滤波平滑数据和标幺值转化对数据信息进行预处理[20]来消除噪声,以提高评估准确性。
虚拟惯量响应功率的计算首先需要求得稳态时新能源的初始功率P0n,m。取tsn,m前Ts时间段内有功功率平均值作为Rn第m组爬坡测试的P0n,m,其计算方法为:
此方法可进一步消除数据采集的噪声,进而可得每组测试期间的增量惯量功率ΔP(iT)如下:
2.3 电网模拟器的测试起止时刻判据
电网模拟器在PCC 处产生的频率变化由于存在控制延迟,无法实时调制出具有特定频率变化率的输入信号所定义的电网频率,易造成爬坡速率无法立刻达到特定的Rn。若按设定的起止时刻tsn,m、ten,m进行惯量评估,则可能产生显著误差。因此,须在PCC 处实际测量频率信号,并对每组惯量响应测试 的 实 际 起、止 时 刻tbn,m和tfn,m进 行 判 断,具 体 方 法如下:
式中:q(q=0,1,…,Q)为设定满足条件的采样间隔数,其中,Q为避免采集数据偶然误差、提高评估抗干扰能力而设定的连续次数;k1、k2为频率变化灵敏系数,可实现不同Rn下判断条件的等比变化,保证判断效果一致,且k1越大,k2越小,tbn,m、tfn,m对频率变化的敏感度越低,为保证敏感度并减少频率波动带来的误差影响,本文k1取0.3、k2取0.7;f0为电网额定频率。
以满足式(10)的tbn,m、tfn,m替换式(8)和式(9)中的tsn,m、ten,m,消 除 了 电 网 模 拟 器 控 制 延 迟 造 成 的 起止时刻误差。
2.4 惯量响应延时补偿
如前所述,新能源惯量响应过程中存在的延时使惯量响应功率与PCC 处的电网频率产生时序上的错位[23],造成惯量评估误差。因此,须对惯量响应延时进行补偿。
根据式(3)可得:
式中:ΔPrefn,m为Rn中第m组爬坡测试的增量惯量功率参考值。
频率开始变化到有功功率增量上升至ηΔPrefn,m的时间为响应延时(参考文献[36]对滞后时间的定义,本文η取10%),则惯量响应的起、止时刻tBn,m和tFn,m下的增量功率分别为:
根据已确定的tbn,m、tfn,m,惯量响应延时Tdn,m为:
式中:dn,m表示Tdn,m与T的倍数关系,取整数。
与文献[23]的方法相比,本文取2 次延时评估均值作为最终结果,减少了单次评估过程中偶然误差的影响。
2.5 新能源等效惯量
如前文所述,新能源发电类型以及虚拟惯量控制方法众多,须提高其惯量评估方法的适用性。本文提出一种基于差分化摇摆方程的新能源惯量连续评估方法,将评估结果平均化处理,得到最终考虑全动态过程的新能源等效惯量。相比于传统方法[19-21],其不受模型阶次与历史数据的影响,无须知道并网设备内部等效电抗,仅通过PCC 处的有功功率和频率信息便可实现惯量评估。
为将式(1)离散化,首先将其转换为时域表达式:
式中:Hv和Dv分别为新能源等效惯性时间常数和虚拟阻尼常数。
将连续模型式(14)转化为离散模型,用差分方程的形式表示为:
整理可得:
当进行惯量检测时,关闭新能源电源除了惯量响应以外的其他辅助功能,使其有功功率变化均来自模拟的惯量响应,Dv可以视为0。在此基础上,得到等效惯性时间常数的计算表达式为:
根据式(13)求得延时Tdn,m,对式(17)进行延时补偿得:
式中:Hvn,m(iT)为Rn中第m组测试的等效惯量连续估计值。
进而得到该组测试的等效惯量Hvn,m为:
对务组Hvn,m求均值,得到最终惯量评估结果:
2.6 离群值修正
测试数据虽经过2.2 节数据信息处理和2.4 节延时修正,但式(18)对Hvn,m(i)进行计算时仍存在波动较大的离群值(主要原因在于计算窗长为单次测量周期T,对数据的敏感度较高),导致惯量计算结果不精确。文献[20]虽提出了直接剔除离群值的措施,但可能导致重要信息的缺失,无法实现测试过程惯量的连续评估。为了解决这一问题,本文提出更为精确的离群值补偿方案。
绝对离差中位数(median absolute deviation,MAD)算法是一种可快速发现样本数据中离群值的算法[17],其中,MAD 表示务样本与中值偏差绝对值的中值。定义斜率为Rn的第m组测试MAD 为Sn,m:
式 中:c为 无 偏 估 计 系 数,为 使Sn,m符 合 正 态 分 布 数据标准差的无偏估计,c=1.482 6;MED{·}为求解样本中位数的函数。
为评定数据点是否满足离群值条件,定义评价离群值偏离中心点的标幺值化指标r为:
r越大,表示Hvn,m(iT)离群幅度越大(在满足正态分布99%的置信区间条件下,Hvn,m(iT)若为离群值,则r通常应大于3)。为连续、准确地获得惯量评估结果,对离群值进行修正:
式中:1-Wr为修正因子,0<W<1(本文取W为0.95)。式(23)可对r较大(可信度较高)的离群值进行大幅度的偏差修正,对r较小(可信度较低)的离群值进行小幅度的偏差修正,优化了惯量评估性能。
2.7 新能源惯量评估流程
本文提出的DCIE 方法全流程如图2 所示。首先,在关闭除惯量响应功能外其他辅助服务的前提下,通过电网模拟器产生基于2.1 节所述的特定测试频率,对并网点测量得到的有功功率和频率数据进行预处理,得到功率初始值。然后,确定每组测试与惯量功率响应的起止时刻,对有功功率测试数据进行延时修正,并求取务采样时刻的等效惯性时间常数。最后,对务测试时间段内的惯量连续评估结果和务组惯量评估结果进行平均,得到精确的新能源等效惯性时间常数。
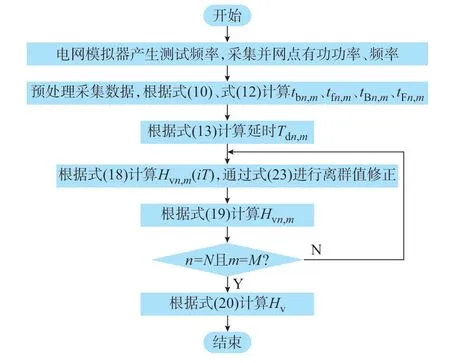
图2 惯性时间常数估计流程图Fig.2 Flow chart for estimating inertia time constant
3 DCIE 方法的效果评估
为验证DCIE 的有效性,搭建了如图3 所示的半物理实验平台。该平台包括:实现惯量模拟控制的dSPACE 快速原型控制器,实现新能源惯量评估算法的TMS320F28377D 外部可编程控制器(以10 ms 时间间隔对PCC 处的功率和频率进行采样)以及模拟图1(a)所示光伏并网系统的RT-LAB OP5600 实时仿真器,光伏并网系统及电网模拟器的电气参数如附录A 表A1 所示,其中,光伏出力参照测试标准[10]取0.7 p.u.。
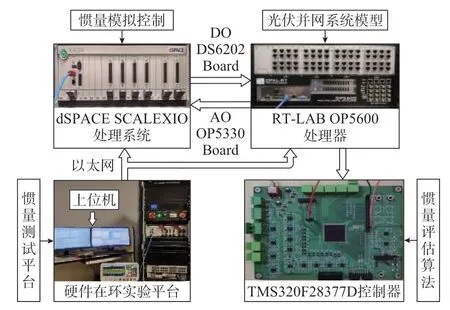
图3 基于RT-LAB 的惯量测试平台Fig.3 Inertia testing platform based on RT-LAB
为实现DCIE 方法,本算例设式(4)中的Rmax、Rmin和测试组数N分别为0.5 Hz/s、0.1 Hz/s 和3[12],设式(6)中的Δfmax为1 Hz[35]。光伏惯量模拟控制采用1.1 节所述方法,Hvset设为6 s,在满足惯量响应时间tr不大于500 ms 的要求下,对比在高响应延迟和低响应延迟下的新能源惯性时间常数的评估结果:
1)低延时惯量响应测试:人工延时Tc为0 ms;
2)高延时惯量响应测试:人工延时Tc为80 ms。
3.1 低延时惯量响应测试
3.1.1 低延时惯性时间常数确定环节
本节以低延时下测试频率信号为0.5 Hz的第1 组测试结果为例,对新能源惯性时间常数确定环节进行演示。在电网模拟器设置频率测试信号的变化起止时刻ts3,1和te3,1分别为33 s 和35 s。如前文所 述,由于电网模拟器存在延迟,通过式(10)可得实际产生 的 频 率 爬 坡 起 止 时 刻tb3,1和tf3,1分 别 为33.06 s 和35.05 s,计算结果与图4(a)所示的半物理实验结果具有高度一致性。可见,该测试时刻起止判据有效避免了传统惯量响应性能评估[10-11]直接采 用ts3,1和te3,1造成的计算误差。
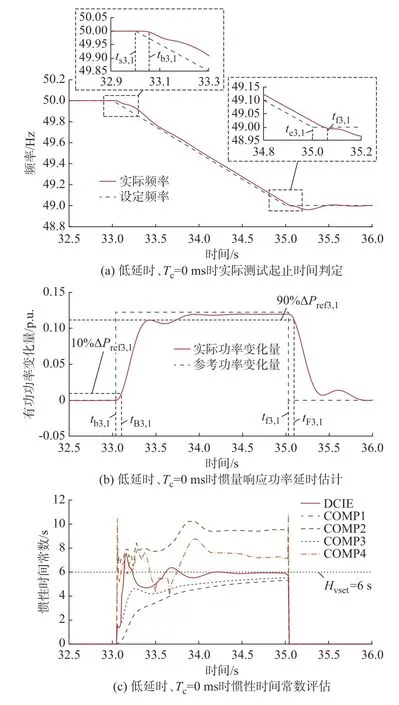
图4 低延时下第1 组测试结果Fig.4 The first group test results under low delay
由图4(b)可见,由于新能源惯量响应存在延时,其实际惯量功率响应未能完全跟踪式(11)确定的参考值ΔPref3,1。进一步,通过式(12)惯量功率响应起止判据,确定惯量响应的起止时刻tB3,1和tF3,1分别为33.12 s 和35.12 s,计算结果与图4(b)所示的半物理实验结果具有高度一致性,最终通过式(13)确定惯量响应的自然延时Td3,1为70 ms。
图4(c)对比了5 种不同惯性时间常数动态评估方法的性能及误差,分别为本文所提DCIE 方法、文献[19]所提基于能量角度的惯量连续评估方法(简称COMP1)、文献[20]所提基于模型辨识的传统方法(简称COMP2),以及分别在COMP1 和COMP2基础上加入本文所提延时补偿的方法(简称COMP3 和COMP4)。由图4(c)可知,COMP1 方法评估的惯性时间常数动态结果整体低于Hvset,COMP2 方法评估的惯性时间常数动态结果整体高于Hvset,加入延时补偿后的COMP3 和COMP4 方法的惯量评估效果要分别优于COMP1 和COMP2 方法,更接近Hvset。而本文所提DCIE 方法的惯性时间常数动态评估结果最接近Hvset,具有更高的准确度。从图4(c)的动态过程可知,DCIE 方法亦具备更快的收敛速度和更高的稳定性。
3.1.2 低延时惯性时间常数全过程评估
图5(a)展示了测试全过程中Rn分别为0.1、0.3、0.5 Hz/s 时PCC 处的频率和有功功率。图5(b)对比了本文提出的DCIE 方法和其他4 种方法在测试全过程中的惯性时间常数的动态评估结果。可见,与3.1.1 节类似,不同评估方法确定的新能源电源惯性时间常数均存在一个稳定前的调整过程。采用文献[13-18]的方式,仅通过某一时刻的新能源惯性时间常数结果进行评估,可能存在较大误差。若采用式(19)和式(20)对其全过程进行统计平均分析(结果如图6 所示),DCIE、COMP1、COMP2、COMP3和COMP4 这5 种方法的惯性时间常数评估结果分别为5.666、5.211、8.096、5.231、7.322 s,误差分别为5.57%、13.15%、34.93%、12.81%、22.03%。可见在测试全过程条件下,本文所提的DCIE 方法的误差最优,且加入延时补偿后的COMP3 和COMP4 方法的结果准确性要分别高于COMP1 和COMP2 方法。
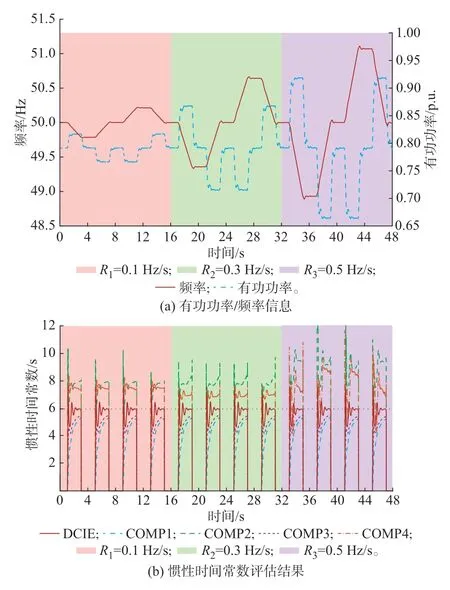
图5 低延时惯量响应测试全过程评估结果Fig.5 Evaluation results of entire process of inertia response test under low delay
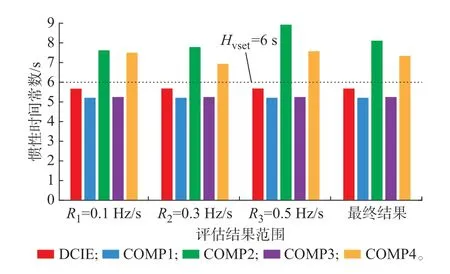
图6 低延时下惯性时间常数统计评估结果Fig.6 Statistical evaluation results of inertia time constants under low delay
通过DCIE 方法得到的务组测试的起止时刻、延时估计和惯量评估结果见附录A 表A2。
3.2 高延时惯量响应测试
3.2.1 高延时惯性时间常数确定环节
如附录A 图A2(a)所示,通过DCIE 方法确定的电网模拟器实际产生的频率爬坡起、止时刻tb3,1和tf3,1分 别 为33.06 s 和35.05 s,与 低 延 时 的 测 试 结果一致。图A2(b)中,通过DCIE 方法确定的惯量功 率 响 应 的 起、止 时 刻tB3,1和tF3,1分 别 为33.2 s 和35.2 s,结合tb3,1和tf3,1进一步确定惯量响应的总延时Td3,1为150 ms,较低延时测试的结果增加了80 ms,与加入的人工延迟Tc=80 ms 一致,验证了DCIE方法计算惯量响应延时的准确性。如图A2(c)所示,高延时下COMP1 和COMP2 方法的评估结果分别低于和高于Hvset,并且COMP3 和COMP4 方法比未进行延时补偿的原方法更接近Hvset。相比之下,DCIE 方法的惯性时间常数动态评估结果最接近Hvset,其收敛速度与稳定性亦高于其他2 种方法。
3.2.2 高延时惯性时间常数全过程评估
高延时下新能源惯性时间常数测试全过程的频率、功率信息及惯性时间常数动态评估结果如附录A 图A3 所示。惯量统计评估的最终结果如图A4 所示。DCIE、COMP1、COMP2、COMP3 和COMP4 这5 种方法的惯性时间常数评估结果分别为5.796、4.945、7.960、5.437、7.724 s,误 差 分 别 为3.41%、17.58%、32.66%、9.39%、28.73%。可知,在高延时测试下,考虑延时补偿的COMP3 和COMP4结果准确性仍分别高于COMP1 和COMP2,DCIE方法的误差仍然显著低于其他方法。
通过DCIE 方法得到的务组测试的起止时刻、延时估计和惯量评估结果见附录A 表A3。
4 结语
本文提出了一种DCIE 方法,设计多RoCoF 的惯量响应测试频率,根据有功功率和频率信息进行惯量响应功率延时计算及补偿,并依据离散化的同步机摇摆方程对新能源惯性时间常数进行评估。在半实物仿真平台测试环境下进行实验分析,得出以下结论:
1)DCIE 方法通过对测试频率爬坡起止时刻和惯量功率响应起止时刻的准确判断,取两者起、止时刻差值的均值,实现了不同程度惯量响应延时的精准估计;
2)DCIE 方法通过补偿方式,将惯量响应功率根据延时结果进行时序上的动态调整,有效降低了延时对惯量评估性能的影响,较现有方法显著提高了惯性时间常数动态估计的准确性;
3)DCIE 方法从不同测试频率斜率与系统频率上下限约束的角度,设计了新能源惯性时间常数评估全过程,可有效指导未来新能源惯量响应测试。
随着新能源大规模并网,其惯量响应能力的测试与评估工作对保障电力系统频率稳定运行愈加重要。DCIE 方法可在惯量响应满足并网规程要求的前提下,实现更为规范全面的新能源惯量测试流程和更为精准的惯性时间常数评估,有助于保障新能源惯量响应满足并网规程要求,亦可为未来辅助服务市场的惯量响应产品提供效益清算依据。
本文在设备、场站层面进行了等效惯性时间常数评估研究,后续可进一步考虑如何在系统层面实现日常运行中的等效惯性时间常数连续评估工作,保障新型电力系统的稳定性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

