基于BP神经网络算法的顶管下穿地表沉降预测研究
李永杰
(中国电子工程设计院股份有限公司)
1 引言
近年来,作为节地型城市基础设施,城市地下综合管廊已经开始在全国大力推广,并且取得良好的经济效益。作为常见的地下管道施工方法,在顶管下穿过程中,地层的沉降和变形是一个重要的研究问题。因此顶管下穿过程中的位移监测对整个工程施工的安全和质量至关重要,而监测数据能够真实反映顶管下穿过程中地层的变形情况,能够有效的控制顶管下穿过程中的顶进速度和注浆压力。同时,通过监测数据的实时分析,对顶管顶进过程中施工参数进行及时的调整,能够预先判断顶进过程中地层变化是否稳定,继续施工是否安全可靠,若出现问题也能够提早制定方案并采取有效措施,防止出现地表坍塌、陷落等情况,确保顶进过程中周围环境的安全。因此,需对顶管施工过程中地表沉降位移进行严格控制,通过对监测数据的处理和分析,对其变形值进行预测,研究其变形规律并对可能出现预警信号采取措施。
目前,关于顶管下穿地层的沉降和变形预测研究已经有一定的成果,包括基于经验公式、数值模拟方法、统计学方法等。然而,这些方法在预测精度和适用性方面存在一些局限性。为了克服现有方法存在的问题。本论文将基于BP 神经网络原理构建数学模型,以某市某矩形顶管施工地表沉降监测数据为例,通过BP神经网络算法进行顶管下穿地层变形的预测,并与实测值进行比对,验证该方法的可行性,从而得出地表沉降规律,为矩形顶管下穿过程中地表沉降控制提供参考依据。
2 BP神经网络
2.1 BP神经网络基本原理
BP 神经网络(Back Propagation Neural Network,BPNN)一种按照误差逆向传播算法训练的多层前馈神经网络[1],是目前应用最广泛的神经网络模型之一。BP 神经网络模型[2]是由输入层、输出层和若干隐含层组成的前向连接模型,同层各神经元间互不连接,相邻层的神经元通过权值连接且为全互连结构(见图1)。

图1 BP神经网络结构
神经网络解决现实问题的原理是通过对输入数据进行有效组织和调整模型参数,以提高模型对数据的预测能力。神经网络通过将输入数据转换成矩阵形式,并将其传递给模型的不同层之间的权重和偏置参数进行计算和调整。这些参数决定了神经网络对输入数据的响应方式。通过对参数进行调整,模型可以自动学习到输入数据中的相关特征,并建立一种映射关系,从而实现对数据发展情况的预测。在训练过程中,神经网络使用反向传播算法,根据预测结果和真实数据之间的差异,计算损失函数,并自动调整模型的参数。通过迭代训练和参数调整,神经网络能够逐渐优化自身的预测能力,在输入新数据时能够做出更准确的预测。
2.2 BP神经网络算法
BP 神经网络算法主要由信号的正向传播和误差的反向传播[3]两个过程组成。在正向传播时,输入信号从输入层经过隐含层的非线性变换,传递到输出层,通过与预期输出进行比较计算误差。若误差不满足预定的要求,则将误差以此进行反向传播[3]。在反向传播过程中,输出层的误差通过逐层反向传递回输入层,根据误差调整网络各层之间的权重和偏置,不断减小误差,完成一次循环。正向传播和反向传播过程交替进行,直到网络输出的误差达到要求或达到预设的训练次数[4]。经过训练后,BP 神经网络能够处理类似的输入信号。将数据输入已经训练过的神经网络中,即可得到相应的预测结果。BP神经网络算法的核心是通过调整神经网络各层之间的权重和偏置,以最小化输出误差。通过反向传播算法实现误差的逆向传递和调整,使网络能自动学习输入数据的特征,并对未知数据进行准确地预测。
3 工程案例应用及分析
3.1 工程概况
本工程起于市政道路西侧始发井,终于市政道路东侧接收井,顶管顶进长度126m,矩形顶管上方为城市主干道,车流量较大,下穿市政道路段顶管覆土厚度16m。该综合管廊为单舱形式,管廊采用6.00mx4.3m 的断面,内部设有给水管和通信管线。本管廊顶管工程自西向东顶进施工,穿越地层主要为中砂层及粉土层,地质条件较差,施工时易发生涌砂涌水、坍塌,易造成地表沉降。拟建场区浅部局部分布有上层滞水,深部砂层内仍分布有承压水。本工程段潜水属渗入开采型,补给方式以大气降水入渗和地表水体渗漏补给为主,以人工开采和蒸发为主要排泄方式。本工程段承压水属渗入开采型,主要接受地下水侧向径流和越流补给,以人工开采及地下水侧向径流为主要排泄方式。
3.2 BP神经网络的建立
BP 神经网络模型用Matlab R2018b软件编写程序,建立模型并进行预测。本工程选取市政道路两侧监测数据为研究对象,在顶管下穿穿越施工影响范围内,道路东、西两侧边坡及路肩位置各布设1个主测断面,每个主测断面布设11 个监测点,与顶管轴线垂直,路肩、边坡监测点1-11平面内水平间距分为5m、8m、6m、5m、3m、3m、5m、6m、8m、5m。
将各监测断面同一天的11 个监测点的数据分别编为一组,共四组,整理得到总样本。将每个观测点的数据按照70:15:15 的比例分成训练样本、测试样本以及验证样本,设置最大迭代次数为1000 次,学习率u=0.2,目标误差为0.001,隐含层层数为35。
在使用BP神经网络进行训练之前,首先需要导入输入和输出数据。其中,输入可以是观测的期数,而输出数据是对应该期的地表沉降累积值。这些数据将被用作训练网络的样本。在网络设置参数后,开始对网络进行训练。BP神经网络的训练过程中,常常使用均方误差(MSE)和模型的相关系数作为评价指标来评估模型的好坏。均方误差是计算预测值与实际值之间的差异的一种常用指标。它衡量了网络输出与实际输出之间的方差,值越小表示网络的预测越准确。而模型的相关系数是评价模型拟合优度的指标之一。它衡量了预测值与实际值之间的线性关系程度,取值范围在-1 到1 之间。相关系数越接近1,表示模型的预测能力越强。因此,通过监控均方误差和模型的相关系数,可以评估BP神经网络的性能,判断模型的优劣,并根据需要进行参数调整和优化,以提高模型的准确性和泛化能力。
3.3 地表沉降预测结果与分析
通过运用Matlab R2018b软件建立BP神经网络模型,从图2可以看出:经过312次迭代计算后,达到设定的约束条件,网络收敛,趋于稳定,于363 次迭代计算后,训练停止。
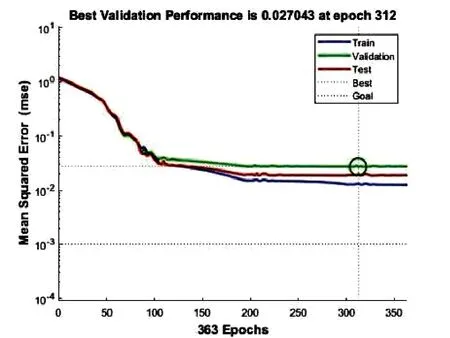
图2 地表沉降训练过程图
图3 为预测沉降量与实际沉降量对比,由图3可知,道路西侧边坡预测沉降量与实际沉降量相差较大,经过对现场施工记录分析,顶管机顶进阶段,千斤顶压力、刀盘的电流强度、减阻注浆量等参数都在不断摸索调整,进入稳定推进阶段,各项参数只有小幅变化。顶管机施工对土体产生扰动,是地表沉降的直接因素,在试顶进阶段,顶管机施工参数的不稳定造成了地表沉降变化的不规律。由图3 可知,道路边坡东侧、道路路肩东侧和道路路肩西侧的预测模型的拟合值曲线均与实测值曲线变化规律基本一致,不过部分节点拟合数据同样存在较明显的波动性,在实测值上下范围内波动,偏差在0.5mm以内。
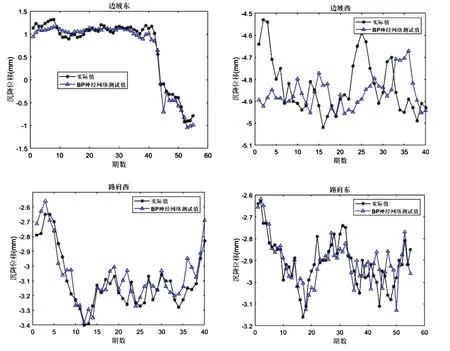
图3 预测沉降量与实际沉降量对比
4 结语
采用BP 神经网络算法,构建出基于BP 神经网络算法的地层变形预测模型,通过调节神经网络的设置参数,并经BP 神经网络训练,能够利用其自学习、自适应的特点,寻找地表沉降复杂规律,能使模型预测结果误差在顶管施工可以接受的范围内,具有较好的工程指导意义。

