某型电动轮自卸车车厢强度分析与尺寸优化设计
雷 杰,倪正顺,熊 涛,王柳平,汤迎红,米承继
(湖南工业大学 机械工程学院,湖南 株洲 412007)
1 研究背景
电动轮自卸车是一种大型的非公路运输车辆,因其装载质量大、工作性能稳定成为矿山场所主要运输工具。随着国内各大中型露天矿的大规模建设和投产,电动自卸车的需求量不断增加。然而,由于电动自卸车的结构复杂且整车质量较大,且常常需要在特殊多变的道路条件下行驶,因此,在这样的工作环境中电动自卸车经常会发生扭转、弯曲等变形现象。车厢作为矿用自卸车最重要的承载部分,其结构设计对整车性能有着重要的影响[1]。自卸车车厢的质量占整车质量的比例很大,对自卸车的油耗影响较大。因此,如何在保证自卸车车厢强度的情况下减轻车厢质量,成为自卸车领域发展所需解决的重要问题[2]。
近年来,随着计算机科学的迅速发展,将有限元仿真分析与尺寸优化的数学模型相结合,得到最优结果集,使尺寸优化方法的实现变得更加快速、方便、准确和可靠[3]。国内外学者对尺寸优化设计进行了较多的研究。Pan Y.J.等[4]将尺寸优化方法应用到汽车电池组外壳的开发设计中,优化后的电池组外壳结构具有10.41%的轻量化增益,同时增强了电池组的动态性能。Zhao X.H.等[5]对精冲机机架进行了灵敏度分析,并采用尺寸优化法对机架进行优化,使得机架质量减轻了12.94%。Li C.等[6]采用尺寸优化的方法对某汽车横梁进行轻量化设计,获得了横梁零件的最佳材料分布,使得优化后的横梁强度满足设计要求,且质量减轻了近40%。叶辉等[7]将尺寸优化方法应用到汽车车身轻量化的开发设计中,以车身零部件结构的板厚为设计变量,以车身刚度为约束条件,将目标定义为车身质量最小进行优化计算,优化结果满足设计要求,且车身质量减轻了14.8 kg。王旭飞等[8]针对电动客车车身,利用有限元软件对车身进行静力学分析和模态分析,采用尺寸优化方法对其进行轻量化设计,优化后的客车车身骨架总质量下降了339 kg。柳占宇等[9]以某型动力集中式动车组车体牵引梁为例,采用尺寸优化方法对其进行轻量化设计,以牵引梁的板厚为设计变量,以符合安全条件为约束条件,以牵引梁质量最小为优化目标进行优化设计,优化后质量降幅达到50.9%,且减重优化后牵引梁满足设计要求。吴青龙等[10]将尺寸优化方法应用到塔式起重机吊臂的布局设计中,以腹板半径为设计变量,臂架顺应性为目标函数,动臂物料体积为约束条件,建立尺寸优化数学模型。通过将原动臂与优化后动臂进行比较,尺寸优化方法可以有效减少动臂质量,增加动臂刚度,降低变形和结构应力水平。
以上研究成果表明,尺寸优化技术已在许多结构轻量化设计方面得到应用。但是利用尺寸优化设计方法,实现自卸车车厢结构轻量化设计研究的文献报道相对较少。基于以上分析,本文以某型220 t自卸车车厢作为优化设计对象,建立车厢的三维模型和有限元模型,并应用CAE分析软件HyperWorks对满载状态下的车厢在6种不同工况下进行有限元分析,得到车厢的应力分布云图。依据强度计算理论,在上述工况下,车厢强度安全系数较高,存在质量冗余问题,故需对车厢进行尺寸优化设计,并对其合理性进行分析校核,保证在满足强度要求的前提下达到减重目标。
2 理论基础
2.1 第三强度原则
σ1为第一主应力且为最大应力σmax;σ3为第三主应力且为最小应力σmin;过一点的所有截面上切应力最大值τmax为
当最大切应力τmax=时材料出现屈服,于是得屈服准则为,将正应力σs换为许用应力σ,得到按第三强度理论建立的强度条件为
2.2 尺寸优化设计
设计变量为x,其目标函数f(x)、约束函数gu(x)和hv(x)是最优设计的3个元素。本文中的设计变量是侧板、前板、底板、U型梁的壳单元厚度,表示为X=[x1,x2, …,xn];目标函数表示为f(X)=f(x1,x2, …,xn);约束函数是设计变量选择的约束条件,其形式有不等式约束gu(X)和等式约束hv(X)。一般优化设计问题的数学模型可以表示如下:
式中:u和v为未知数的个数;m和p为维数(设计的自由度);D为定义域。
当m=p=0时称为无约束优化问题,m≠p≠0称为约束优化问题。f(X)、gu(X)和hv(X)都是线性函数,称为线性优化问题;f(X)、gu(X)和hv(X)其中有一个是非线性函数,称为非线性优化问题[11]。
3 电动轮自卸车车厢有限元模型建立与验证
3.1 电动轮自卸车车厢几何模型建立
矿用自卸车车厢一般由底板、侧板、前板、U型梁等组成,各部分均采用钢板焊接而成。其中底板厚度为20 mm、前板厚度为15 mm、侧板厚度为10 mm、前端板厚度为5 mm、U型横梁厚度为12 mm、U型纵梁厚度为15 mm。根据某公司提供初始的车厢图纸,建立的自卸车车厢原始模型如图1所示。

图1 车厢整体模型Fig.1 Overall model of the carriage
在保证有限元分析可靠的基础上,可根据有限元分析前处理及求解器特点在保证车厢主要力学特性的前提下对其进行适当简化,主要简化原则如下:1)省略一些非承载件及装饰件,如装饰灯、尾部链条;2)建模过程中对于一些施加载荷和约束的工艺孔要精准布置,非重要工艺孔可省略;3)对于车厢骨架上某些形状不规则的构件可在保证受力条件下适当简化。简化后建立的自卸车车厢模型如图2所示,后续将以该模型为对象进行有限元分析。

图2 简化后的车厢模型Fig.2 Simplified carriage model
3.2 有限元模型建立
Hypermesh软件是美国Altair公司开发的一款有限元分析软件,其特点是它具有强大的有限元网格划分前处理功能,同时使用方便灵活,并能够与众多CAD软件和有限元求解器进行数据交换,可以直接将车厢三维模型导入Hypermesh中。
3.2.1 材料属性
这些例子揭示了许多有关人们使用技能方式的问题,人力资本理论从经济学角度做了详细的描述。可是,传统上这些是教育学研究的领域。通过考察人们如何从经济学角度思考、学习和使用技能,表明经济学在这些问题上作出了贡献。
车厢母材为低合金高强度结构钢,整体由若干块钢板焊接而成,表1所示为车厢材料参数。

表1 车厢材料参数Table 1 Parameters of carriage materials
3.2.2 网格划分
分析车厢整体尺寸,车厢板材主体尺寸远大于厚度方向尺寸,故采用壳单元 Pshell在Optistruct 中对车厢板块结构进行离散。散装货物是车厢主要载荷。根据相关标准对散货建模,采用 Pmass质量单元进行离散化,自卸车正常工作过程中货物和车厢保持相对静止状态,即货物和车厢无相对位移,通过质量单元和车厢节点耦合,将货物重力传递到车厢[12]。另外,橡胶垫用Psolid实体单元进行结构离散。根据堆装的体积及载质量,货物质量为220 t。根据上述要求划分的网格模型单元数量为153 872,节点数量为145 919,网格模型见图3。

图3 车厢网格模型Fig.3 Carriage mesh model
3.2.3 有限元分析边界条件
满载静止、制动、转弯、转弯制动、匀速等5种工况下车厢未被升起,车厢底部纵梁直接与橡胶垫接触,故这5种工况下将橡胶垫下表面定义为零位移约束;同时定义斗铰支孔径向和侧向零位移约束,如图4所示。
图4 车厢未升起时约束Fig.4 Restraint condition with the carriage lowered
满载举升工况,即车厢刚被举起时,对斗铰支孔和举升缸支座孔进行全约束,如图5所示。

图5 车厢升起时约束Fig.5 Restraint condition with the carriage raised
3.3 计算结果及评价
定义车厢材料参数和6种工况的边界条件后,提交Optistruct计算可以得到6种工况下的静力分析结果。
满载静止工况主要研究自卸车在平整路面静止时的受力;满载匀速工况主要研究自卸车在平整路面匀速行驶时各部分的受力情况;满载转弯工况主要用来模拟自卸车在急转弯时,在离心力作用下,分析车厢各部分的受力状态;满载制动工况模拟自卸车在紧急制动时,在惯性力作用下,车厢各部分的受力状态。其中车厢在满载匀速工况主应力分布云图见图6。车厢各工况主应力云图见图7。

图6 满载匀速工况主应力分布云图Fig.6 Cloud map of principal stress distribution under the full load uniform speed working condition
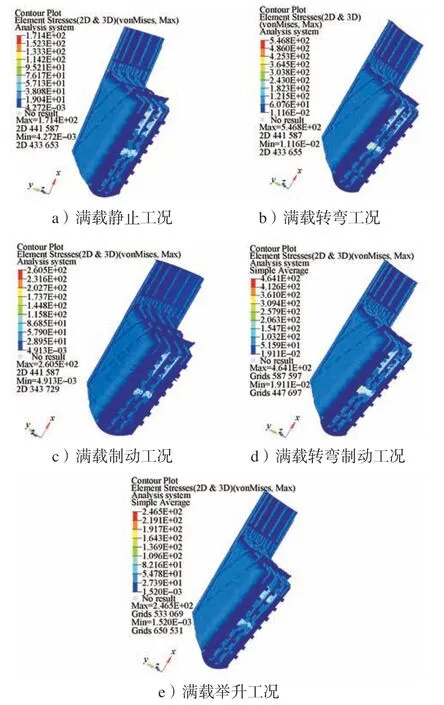
图7 不同工况的主应力云图Fig.7 Principal stress cloud map under different working condition
综合考虑自卸车在实际中的典型工况,上述工况的加载方式如下:1)满载静止工况。工作条件是自卸车以静止或恒定速度运行,在这种工作状态下,车厢上的负荷是载质量和车厢自重的总和,惯性加速度取9.8 m/s2,方向向下。2)满载匀速工况。行驶方向的加速度取1.39 m/s2,垂直加速度取9.8 m/s2,方向向下。3)满载转弯工况。考虑侧向离心力作用,侧向加速度取2.94 m/s2,垂直加速度取19.6 m/s2。4)满载制动工况。行驶方向加速度取-1.39 m/s2,垂直加速度取11.76 m/s2。5)满载转弯制动工况。侧向加速度取值2.94 m/s2,行驶方向加速度取-1.39 m/s2,垂直加速度取19.6 m/s2,方向向下[13]。6)满载举升工况。此工况是满载下车厢刚被液压举升缸举起状况,此时车厢处于静止状态,故仅考虑重力加速度,取9.8 m/s2。
3.3.2 车厢静力分析位移结果
静态变形是衡量车厢刚度水平的一个标准,车厢6种工况位移云图如图8所示。
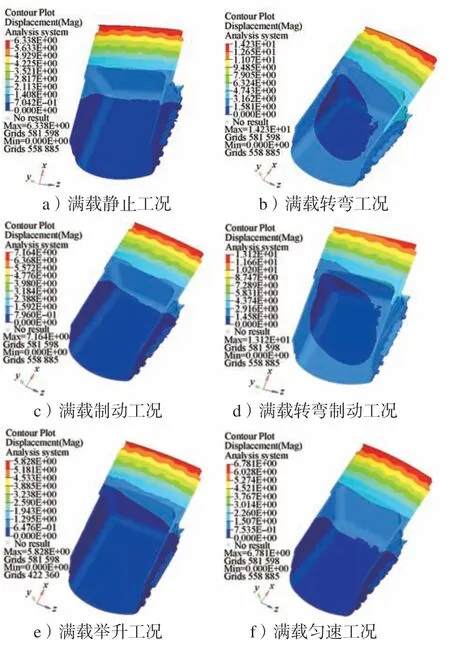
图8 不同工况的位移云图Fig.8 Displacement cloud map under different working conditions
3.4 车厢有限元模型验证
为验证车厢有限元模型的准确性,进行了车厢应变测量实验,通过应变片测量车厢相应测点的应变数据,并与仿真数据对比。
自卸车工作环境的道路多为坑洼路面,高低起伏,环境恶劣,实验工况测试路面最大坡度为17%,最小转弯半径为17 m。
MOPS(miuion operation per second)强度测试系统连接半桥应变片和温度补偿片,所有测点均在空载状态下贴片。测点J5-1位于左侧车厢铰链支座内侧立板与车厢横梁连接处,如图9a所示,对应仿真测点为U型纵梁铰链支座孔左侧。测点J5-2位于右侧车厢铰链支座内侧立板与车厢横梁连接处,如图9b所示,对应仿真测点为U型纵梁铰链支座孔右侧。

图9 测点布置示意图Fig.9 Measurement point layout schematic diagram
现场根据各测点引线长度、应变片的灵敏度和电桥连接方式,使用HBMK3602标准应变校准仪对应变片进行校准。本试验中使用的应变花灵敏度系数为2.12。测试时,各点应变信号经放大、滤波、A/D转换成数字量后进入计算机分析系统,并利用德国Caesar公司的MLab、MGraph信号采集分析软件进行分析处理。整个系统按照GB/T 27025—2008《校准和检验实验室能力的通用要求》检验规程进行了校验[12]。在每个测点均匀粘贴45°应变花,最大主应力中杨氏模量E取2.07×105MPa,泊松比μ取0.27。
电动轮自卸车车厢等钢结构选用钢板材质为Q690高强度低合金调质钢,σb为840 MPa,屈服强度σs约为700 MPa,按许用应力安全系数取1.5考虑,许用应力σa值约为466 MPa。根据以上要求所得6种工况的实验值与仿真值如表2所示。
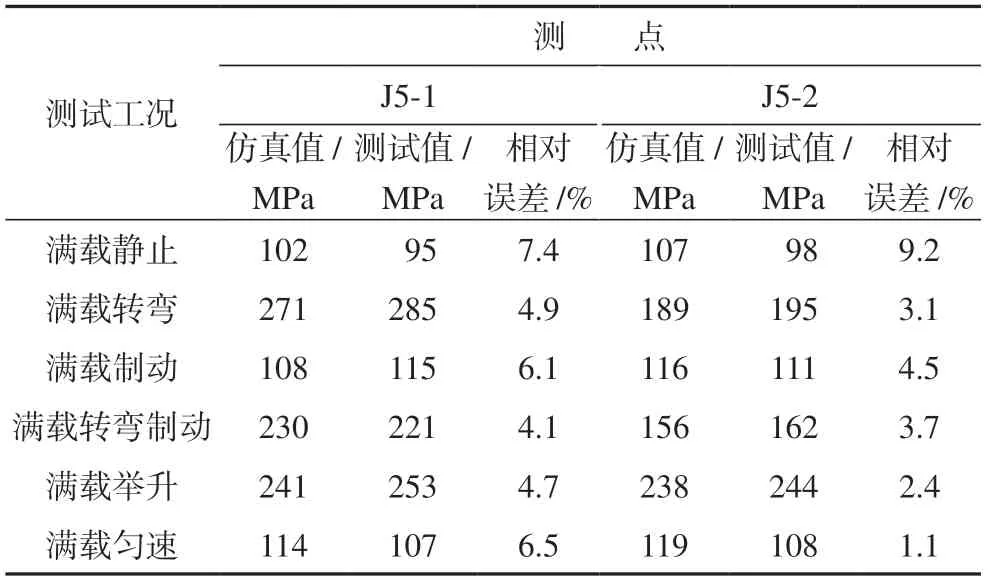
表2 不同工况下的实验值与仿真值Table 2 Experimental and simulation values under different working conditions
通过实验值与仿真值的对比可以看出两者数据相差不大,验证了有限元模型的准确性,为后续进行尺寸优化设计奠定了基础。
4 车厢强度分析
6 种工况的强度分析基本反映出车厢的强度水平,最大应力出现在纵梁的斗支孔处,6种工况的最大应力为558 MPa,小于所用材料的屈服强度700 MPa,因此整个车厢基本能符合设计的要求。根据第三强度理论和许用应力σa值约为466 MPa计算安全系数,计算结果见附表1。
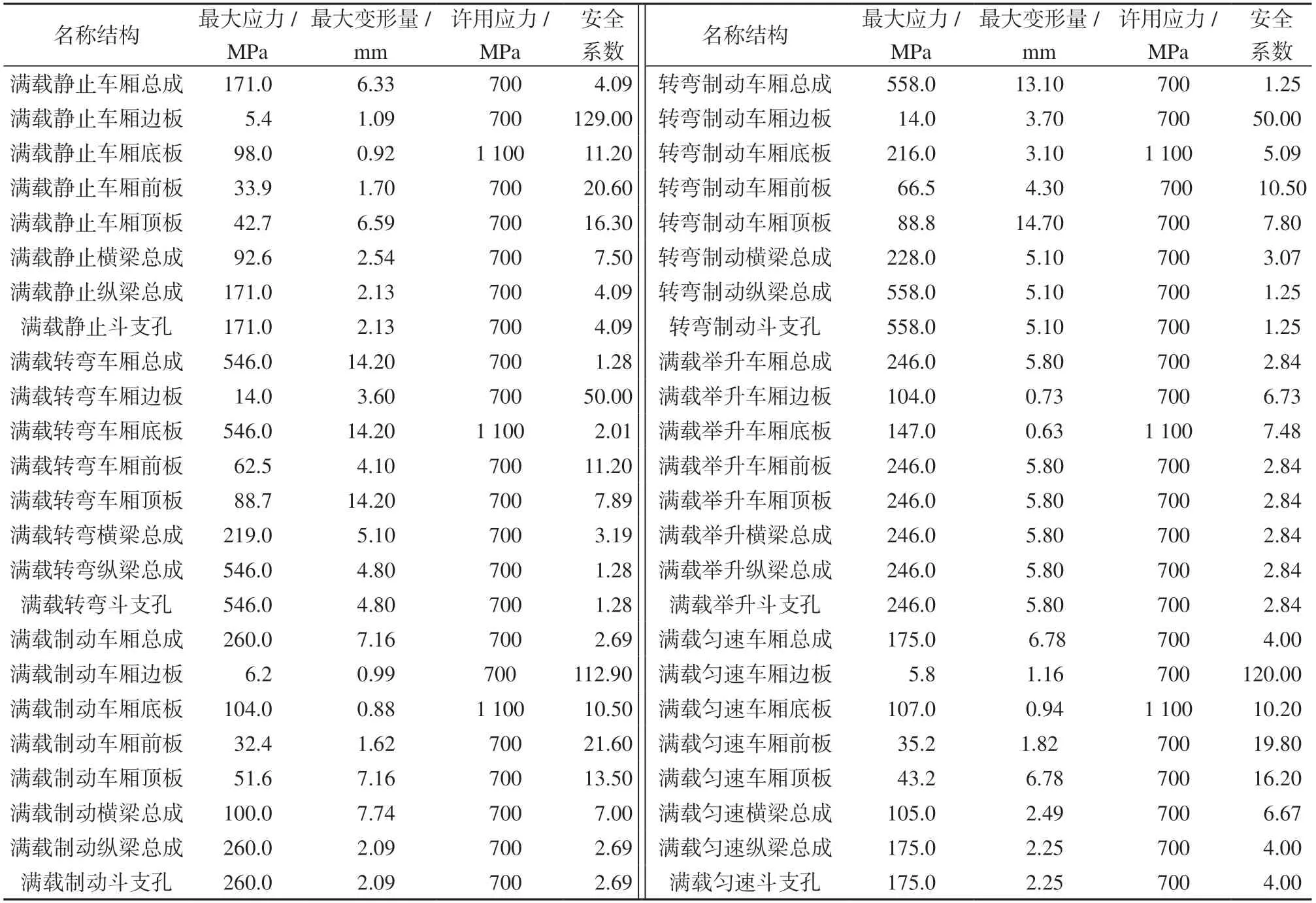
附表1 各工况下车厢应力及变形结果Table 1 Stress and deformation results of the carriage under various working conditions
由附表中数据可知,在上述工况下,车厢强度安全系数较高,存在质量冗余问题,因此需要对车厢进行轻量化设计。
5 车厢尺寸优化设计
为了优化自卸车厢钢板的厚度,需要在Optistruct中设定设计变量、目标函数和约束函数等参数,具体设定步骤如下[10]:
1)定义设计变量x。根据有限元分析考虑将车厢侧板、前板、底板、U型梁等对车厢优化目标影响较大的板厚定义为设计变量,依据设计要求允许的变动范围对设计变量进行取值,如表3所示。
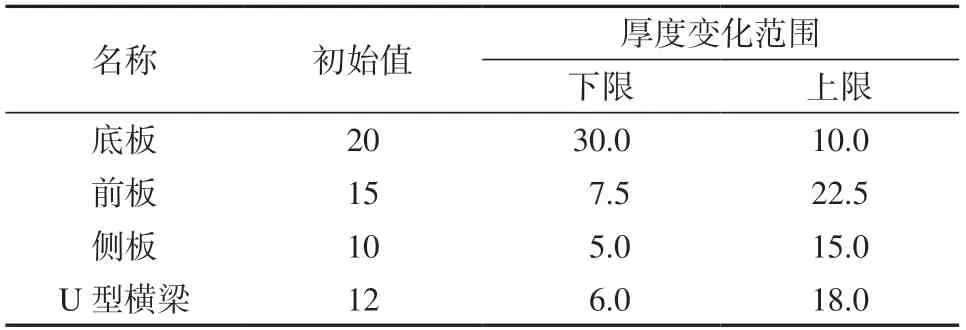
表3 车厢设计变量Table 3 Carriage design variablesmm
2)将设计变量与壳单元的厚度属性相关联。
3)定义响应。在响应(Responses)子面板中定义质量(Mass)和应力(Von-Mises)两个响应。
4)定义目标函数。定义质量最小化为目标函数,选择目标(Objective)面板,将质量响应(Mass)定义成目标函数。
5)定义约束。由于车厢板块材料的屈服极限为700 MPa,将车厢板块上的Von-Mises应力的最大值设定为700 MPa。
根据车厢强度分析结果,选择应力最大的满载转弯制动工况进行厚度优化,经Opstistruct优化迭代14次得到车厢板块的厚度值,优化前后车厢板块厚度结果见表4,优化结果云图如图10所示。

表4 车厢板块厚度优化结果Table 4 Optimization results of carriage panel thickness
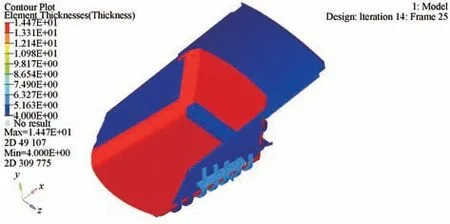
图10 优化结果云图Fig.10 Optimization effect cloud map
将优化后的结果重新进行仿真分析,得到的分析结果如表5所示。从表中可以看出优化后的车厢在不同的工况下应力都有一定幅度的上升,但仍满足车厢的使用要求,而车厢质量降幅达到了22.9%,满足了轻量化设计要求。
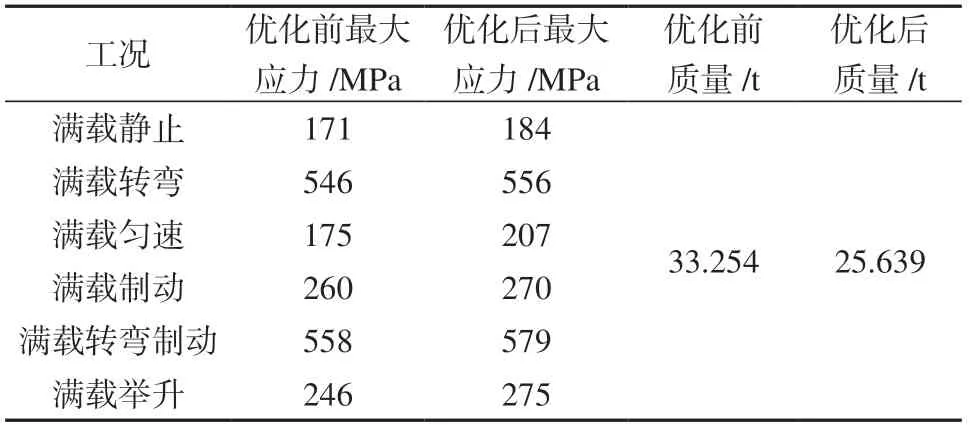
表5 优化前后各工况应力结果对比Table 5 Comparison of stress results under various working conditions before and after optimization
6 结语
本文以某型电动轮自卸车车厢作为研究对象,建立了车厢的三维模型和有限元模型,并应用CAE分析软件HyperWorks对车厢在不同工况下进行了有限元强度分析,得到车厢的应力分布云图。依据强度计算理论,在上述工况下,车厢强度安全系数较高,存在质量冗余问题,故需对车厢进行轻量化化设计,基于Optimization模块对车厢厢体结构进行尺寸优化设计,以该自卸车车厢板块厚度作为设计变量,在保证结构应力满足设计要求的前提下尽量减少车厢的质量,最终优化后的车厢质量降幅达到22.9%,将优化后的各工况应力结果与优化前对比满足强度要求,实现了车厢轻量化设计目标。

