破碎岩体隧道洞口开挖诱导滑坡与古滑坡耦合分析

祝方才，周俊杰，赖国森，晏 仁，刘海媚

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.中铁北京工程局集团 第二工程有限公司，湖南 长沙 410116）

山区修建隧道时，由于选线受地形条件等限制，其进出口位置可能选择在高陡边坡地段，当岩体破碎时，滑坡和崩塌等会影响进洞安全。丁恒等[1]通过实时监测数据、数值模拟等方法研究了古滑坡复活变形特征及复活成因，认为古滑坡复活主要受地形地貌、地层岩性、降雨和煤层开采共同作用的影响。韩斌等[2]分析了复杂破碎露天边坡加固措施的作用机理及适用范围。陈记等[3]通过对现场监测数据分析，提出了竖向钢花管群桩+斜向预应力锚索框架梁的加固治理措施。潘家铮[4]在建筑物抗滑稳定性中，提出了抗滑稳定的最大最小原理。陈祖煜[5]基于Drucker准则和Sarma斜分条边坡分析方法，使用虚功原理和塑性力学的上、下限定理，对潘家铮最大最小原理进行了证明。陈祖煜[6]基于塑性力学的上下限定理，将垂直条分法与斜条分法推广到各种支护结构主动土压力与地基承载力计算领域。何毅等[7]基于极限分析上限定理，以坡顶存在裂隙边坡为研究对象，借助平面应变对数螺旋线对含裂隙边坡的稳定性进行求解和分析。沈尧亮等[8]根据刚体平衡条件分析了传递系数法力学机制。郭海强等[9]基于可靠度传递系数法，通过实例对比说明传递系数显示解法与隐式解法存在的差异。屈春来等[10]基于极限分析上限定理，建立了3种模式的非均质成层边坡刚性多滑块破坏机制，并得出边坡极限承载力上限解。田泽润等[11]基于边坡塑性极限理论，通过组合对数螺旋线破坏机构，推导出双层均质边坡的临界高度方程，并通过强度折减法获得边坡的稳定性系数。

为研究某破碎岩体隧道的洞口段切坡引起的滑坡与古滑坡耦合作用，本研究拟根据钻孔测斜和现场踏勘等资料，圈定潜在滑动面，基于强度折减法搜索危险滑动面，利用上限分析法和不平衡推力传递法，计算加固前后边坡安全系数，并与强度折减法对比，供工程设计和施工参考。

1 工程概况

云南某高速公路隧道进口段仰坡地貌为低中山地貌，自然坡度在20°～35°之间，坡体大多为阶梯状耕地，表层为粉质黏土，基岩为强风化板岩和中风化板岩，岩体较破碎，如图1所示。

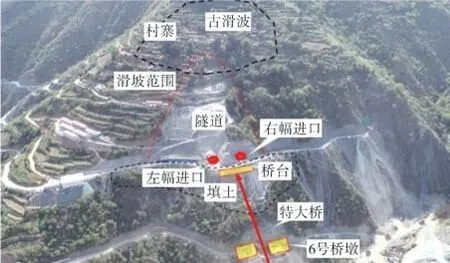
图1 某高速公路隧道滑坡全貌Fig.1 Overall view of the landslide in a certain highway tunnel

因隧道建设的需要，在坡体上进行仰坡及便道开挖，坡体上方有古滑坡，下方为拟建隧道、特大桥、互通匝道桥等工位。隧道施工时开挖坡体前缘，导致坡体原有应力状态产生变化，坡体前缘抗力降低，坡体向临空区产生变形，在隧道掌子面施工开挖等情况下，隧道仰坡的变形范围及深度不断发展扩大，形成滑坡体，并有进一步扩大变形趋势，严重危及坡体上村寨安全和隧道及下方桥梁建设安全，因此，提出利用钢管桩、锚索框架梁和抗滑桩对滑坡区域进行加固处理，如图2所示。

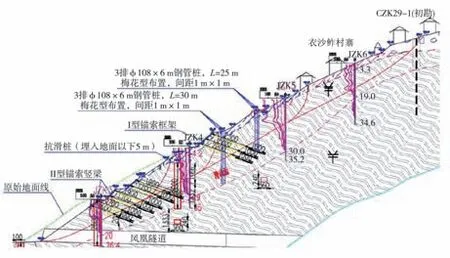
图2 治理措施断面图Fig.2 Cross section map of governance measures

2 钻孔测斜分析

钻孔测斜仪的布置要控制滑坡的前缘和后缘，前后缘至少各布置一个钻孔，尽量利用地质勘探钻孔，根据现场踏勘，布置在变形大并可能发生破坏的部位，或地质上有代表性地段。钻孔应穿过潜在滑动面，直至稳定的基岩，如图3所示。

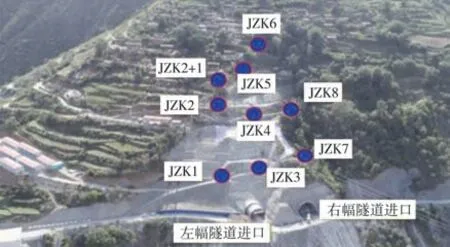
图3 测斜孔布置Fig.3 Layout of clinometer boreholes

如图3所示，JZK3位于边坡隧道洞口上方，JZK4位于边坡中部和古滑坡下部，JZK5位于古滑坡坡脚，JZK6位于JZK5上方古滑坡坡体，JZK3～JZK6断面位于同一剖面线，故选取JZK3、JZK4、JZK5、JZK6的4个监测点数据进行对比分析。

3 数值模拟

基于强度折减法，利用Midas GTS三维有限元软件根据B样条曲面拟合方法，先拟合出四层地层的曲面图，岩土力学参数如表1，随后生成实体单元后经过切坡得到完整的三维地质模型，如图4所示。

表1 边坡各土层和加固材料参数Table 1 Parameters of soil layers and reinforcement materials

3.1 切坡对古滑坡的影响

基于强度折减法结合Midas GTS软件研究边坡的稳定性，边坡出现危险滑动面时，折减系数为其强度储备系数或安全系数，研究表明，滑坡破坏的主要位置即最大剪应变发生的区域，塑性区贯通判定主要依据剪切应变，切坡前后危险滑动面如图5所示。

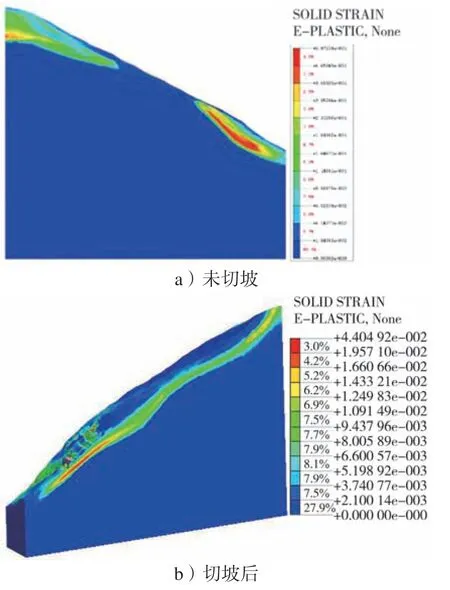
图5 切坡前后的塑性区分布Fig.5 Plastic deformation zone before and after slope cutting

由图5可知，由于隧道洞口切坡，导致仰坡塑性区与古滑坡塑性区贯通，仰坡开挖诱导古滑坡复活,古滑坡与新滑坡之间产生联动变形。

3.2 滑动面的确定

各监测点位移监测曲线如图6所示，确定潜在滑动面如图7所示。

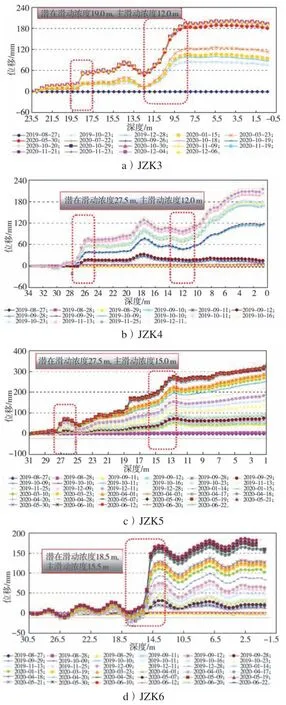
图6 各监测点位移监测曲线Fig.6 Displacement monitoring curves of each monitoring point

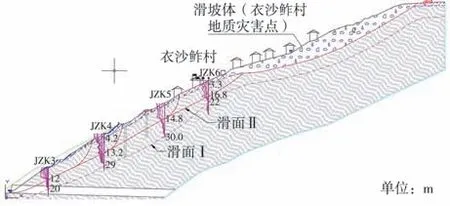
图7 滑动面位置Fig.7 Sliding surface location

根据JZK3位移监测曲线可知该监测点在深度为12 m和19 m处的累计相对位移发生较大变化，结合JZK4、JZK5和JZK6监测点的累计相对位移发生较大变化的位置，可确认主滑动面为滑动面Ⅰ，潜在的深层滑动面为滑动面Ⅱ。

基于强度折减法，利用Midas GTS三维有限元软件生成地质模型计算后可以得到边坡的滑动面，如图8所示；利用Matlab的Fmincon函数[12]对极限分析上限法目标函数进行优化处理可得上限分析法滑动面，如图9所示。对比图8、图9可以看出，二者之间的滑动面相近，因而可以看出强度折减法得到的滑动面同极限分析上限法的滑动面基本一致。

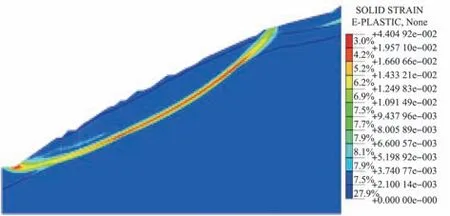
图8 强度折减法的边坡滑动面Fig.8 Slope sliding surface using strength reduction method

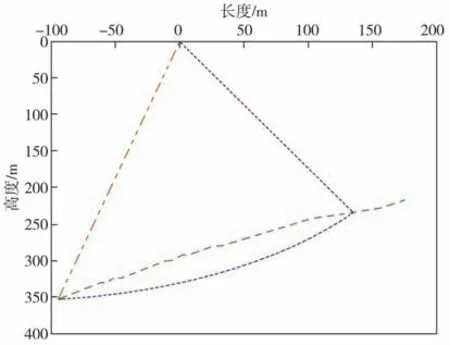
图9 极限分析上限法滑动面Fig.9 Limit analysis upper limit method for the sliding surface

4 稳定性分析

4.1 传递系数法

使用传递系数法隐式解法[13]进行边坡稳定性计算，由图10可得边坡第i条块的推力计算公式：

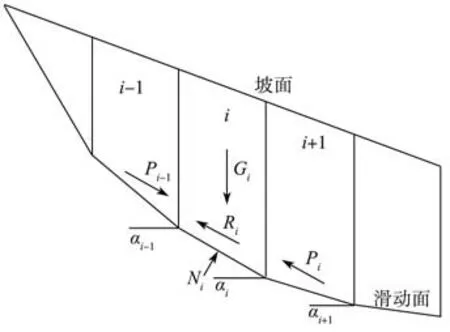
图10 条块受力简图Fig.10 Block force diagram

传递系数隐式解法计算安全系数公式为

对于本文，工程施加的抗滑力为抗滑桩的抗力以及锚杆的拉力，即：

式（1）～（3）中：Ti为第i个滑块产生的滑动力；Ri为第i个滑块产生的抗滑力；Tn为第n个滑块的滑动力；Rn为第n个滑块的抗滑力；Pn为工程施加的抗滑力；αi为第i个滑块滑动面与水平面的夹角；Gi为第i块段的质量；φif为第i块滑体沿滑动面经折减后的内摩擦角；P为抗滑桩抗滑力设计值；T为锚杆拉力设计值；ξ为锚杆与水平方向夹角；ci为第i块滑体滑动面处土的黏聚力；li为第i块滑体沿滑动面的长度；ψj为第i-1块段的剩余下滑力传递至第i块段时的传递系数。

滑动面位于强风化破碎基岩内，其平均深度约13 m，假定该滑坡滑动面呈折线状，为节省计算量，每条取20 m宽岩土体，如图11所示。抗滑桩设置于第8分段及第15分段，锚杆设置于第13分段、第16分段、第17分段处。

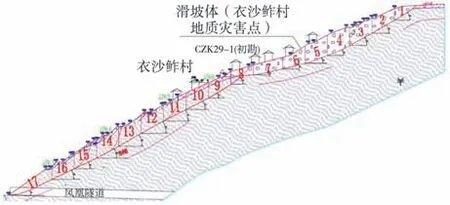
图11 边坡分段计算简图Fig.11 Slope segmentation calculation diagram

不考虑施加抗滑桩、锚杆等支护结构时，其安全系数计算公式为

传递系数法各分段的参数见表2。

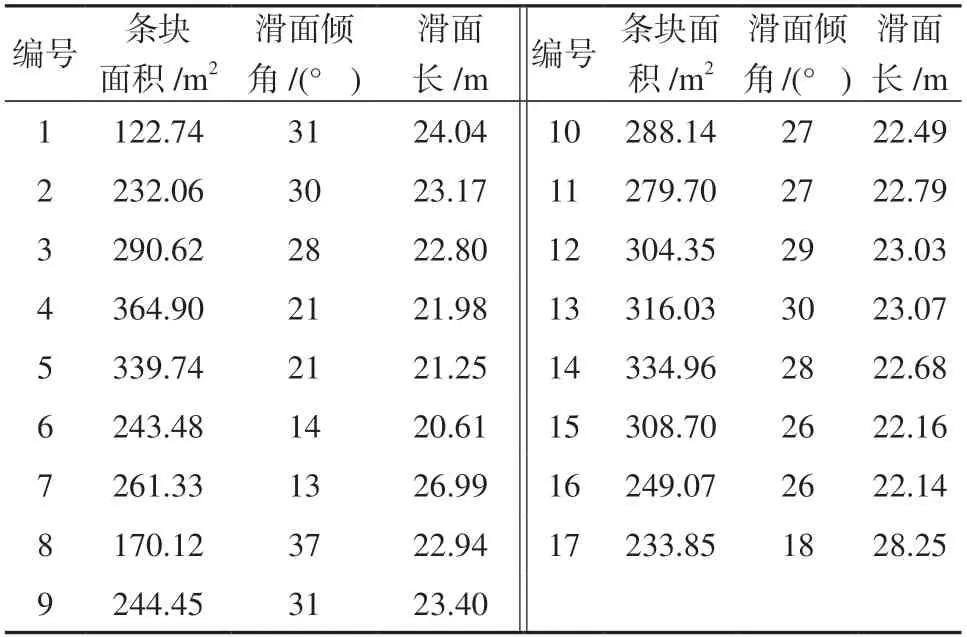
表2 传递系数法各分段参数Table 2 Segmentation parameters using transfer coefficient method

4.2 极限分析上限法

极限分析上限法是通过构筑一塑性破坏机构，塑性破坏机构满足运动许可速度场，通过虚功率求解的荷载为真实破坏荷载上限值，通过上限法求解的荷载一定比真实的应力场相对应的极限荷载值大。

结合洞口仰坡地形地貌以及隧道施工要求，将该边坡设定为5级台阶边坡，台阶参数如表3所示。

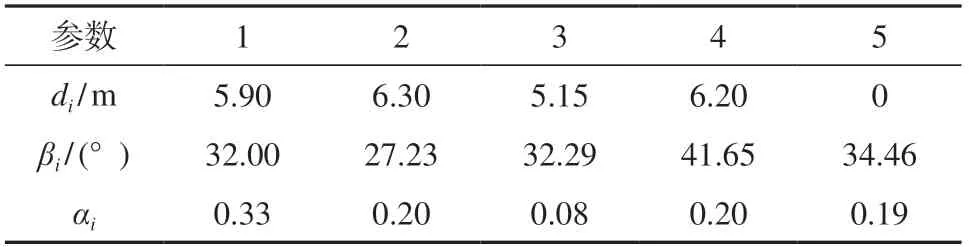
表3 隧道洞口台阶参数Table 3 Tunnel entrance step parameters

隧道洞口仰坡支挡结构断面如图12所示，设破坏面AK为对数螺旋面[14]，破坏面通过坡脚，滑动体ABCDEFGHIJK绕旋转中心O做旋转运动，而对数螺旋面AK以下的土体保持静止不动。AK面为薄层速度间断面，由几何关系可知：

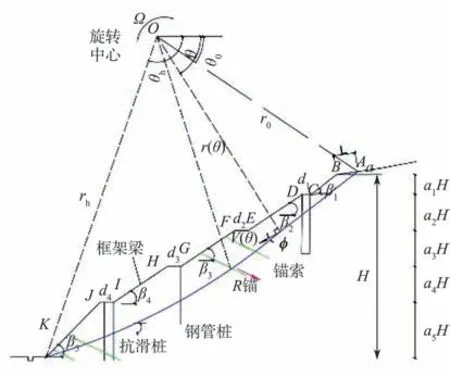
图12 边坡破坏模式图Fig.12 Slope failure mode diagram

利用坐标变换，H/r0和L/r0可用θ0和θh表示：

式中：d1～d5为各级平台宽度；β1～β5为各级边坡倾角；α1～α5为高度系数；H为边坡总高度；r0为线段OA的长度（对数螺旋线初始半径）；θ0为线段OA与水平面夹角；θh为线段OK与水平线夹角。

4.2.1 外功率

借助叠加法求解ABK区域土体自重的外功率。直接从“ABK”区域积分求解土体自重做的外功率较为复杂，故采取叠加法来间接进行计算和求解，即分别求出“OAJ”“OAB”“OBC”“OCD”“ODE”“OEF”“OFG”“OGH”“OHI”“OIJ”“OJK”区域由于土重力做功的功率，对应为W1～W11，通过叠加法求出“OAK”区域的重力外功率WABK。由于框架梁和锚杆数量相对较少，虽钢筋混凝土重度大于土体，可近似把框架梁的重度等效为土体重度来考虑，ABK区域重力外功率可表示为

式（7）（8）中：Dz为抗滑桩的间距；γ为土体重度；r0为OA段长度；Ω为对数螺旋线的角速度；

当n≥2时，

f5～f11可由式（13）（14）求得。

现场施工采用两排抗滑桩及一排钢管桩加固边坡，相对于抗滑桩而言，钢管桩截面面积较小，分担抗力有限，计算时不考虑钢管桩抗力。抗滑桩抗力外功率为

式中：Wz为抗滑桩外功率；P1、P2分别为第一根、第二根抗滑桩所提供的抗力，作用点位于桩悬臂段的中点处；V1、V2分别为第一根、第二根抗滑桩处间断面的速度；ri为抗滑桩滑动面处对数螺旋线半径；θ1、θ2分别为第一根、第二根抗滑桩处对数螺旋线与水平面的夹角。

初春之际，柳枝就开始抽出嫩绿的新芽，那抹绿会让人产生色觉联想，绿色是生命之光，是生命之色，看到它就让人想起生机勃勃的春天，就意味着寒冷的冬天即将过去，充满希望的春天将要来临，“柳”是春之信者就源于人们的这种色觉联想。因发音相似，故用“柳”意“留”，用“柳”表达惜别之情，这其实是人们的听觉联想在发挥作用。

令λ=P1/P2，代入式（15）得：

则λ为第一根桩和第二根桩的抗力比例系数，由于第一根抗滑桩支挡边坡的高度与第二根抗滑桩的高度相当，故可以判断第一根抗滑桩的抗力不大于第二根桩的抗力[15]。

锚索外功率[15]主要来自于锚固段的拉力：

锚索拉力外功率计算关系图如图13所示。

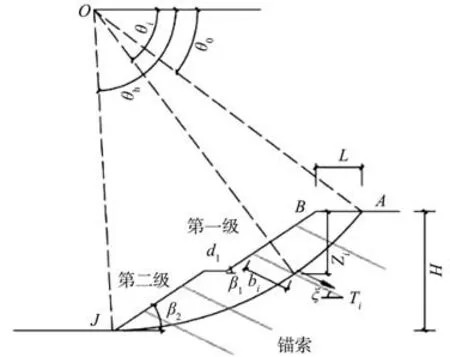
图13 锚索拉力外功率计算Fig.13 Calculation of external power of anchor cable tension

滑面内能损耗发生在间断面AJ，能量损耗率CAJ微分可由该面微分面积rdθ/cosφ与黏聚力和速度的乘积计算[15]，可表示为

4.2.2 安全系数计算

代入求得边坡的临界高度Hcr(θh,θ0)为

通过强度折减法来确定安全系数K值，即：

式中：c、φ分别为黏聚力及内摩擦角；cf、φf分别为折减后黏聚力及内摩擦角。

利用下式求解K：

由式（21）可知，θ0，θh为未知变量，其它参数可根据实际边坡确定。

根据极限分析上限定理，式（21）中K是θ0和θh的函数，隐含K，当θ0和θh满足条件

时，则函数f(θ0,θh)存在极小值时即为边坡安全系数K的解。将式（21）中安全系数K作为目标函数，采用约束非线性最优化方法求解，目标函数及边界条件为

安全系数K实际为隐函数，本文基于Matlab 2020平台，利用二次优化迭代方法或内点优化迭代方法[12]进行迭代计算。

5 计算分析

将各项参数代入公式后，由极限上限法求得未考虑锚索拉力和抗滑桩抗力，安全系数K=0.918，仅考虑锚索拉力作用，安全系数K=1.121，考虑锚索拉力作用及抗滑桩抗力后，安全系数K=1.373。由传递系数法可知未考虑锚索拉力和抗滑桩抗力，安全系数K=1.045，仅考虑锚索拉力作用，安全系数K=1.181，考虑锚索拉力作用及抗滑桩抗力后，安全系数K= 1.381。由数值模拟结果可知，未考虑锚索拉力和抗滑桩抗力，安全系数K=0.975，仅考虑锚索拉力作用，安全系数结果K=1.175，考虑锚索拉力作用及抗滑桩抗力后，安全系数K=1.403。边仰坡加固前后安全系数见表4，安全系数结果见表5。

表4 边仰坡加固前后安全系数Table 4 Safety factors before and after slope reinforcement

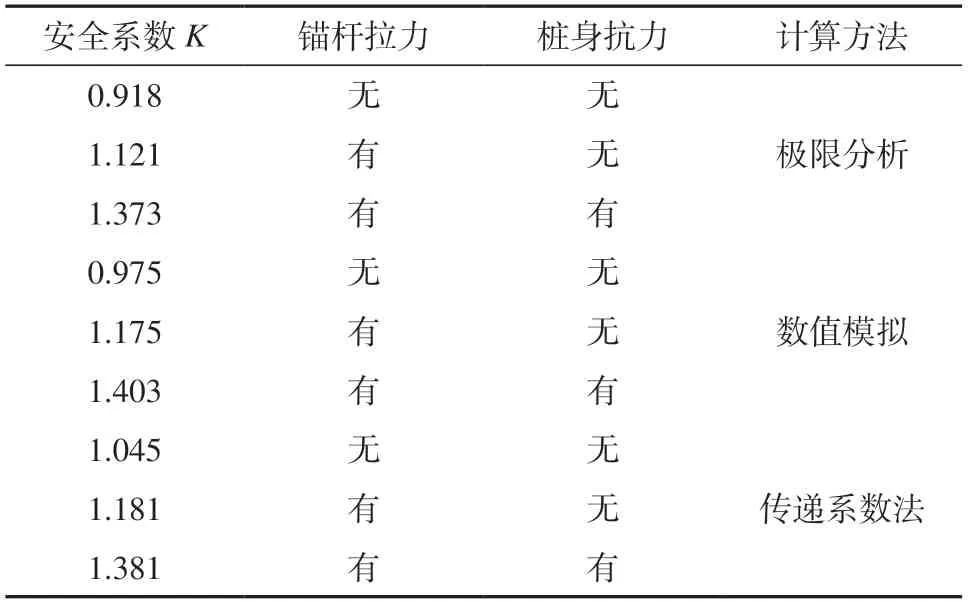
表5 安全系数结果Table 5 Safety factor results

对比上限分析法、传递系数法和数值模拟结果可知，数值模拟方法与极限上限法、传递系数法计算获得的安全系数基本一致，其中，传递系数法计算结果与数值模拟结果在施加抗滑桩及锚杆支护后的结果相差0.5%，上限分析法与数值模拟在施加抗滑桩与锚杆支护后相差仅为2.2%。其原因在于：数值模拟方法与上限分析法、传递系数法的计算原理不同，上限分析法未将土层分层以进行简化，土体重度参数选取较小，计算结果偏小。

6 结论

1）基于钻孔测斜数据和现场踏勘，得出边坡潜在滑动面，分析古滑坡与新滑坡耦合作用机制；

2）基于Midas GTS折减强度有限元分析得出危险滑动面，与边坡潜在滑动面位置相近；

3）基于潜在滑动面利用不平衡推力传递法计算加固前后安全系数，将滑动面近似假设为对数螺旋线，根据地形分为5级台阶进行极限上限分析，得出不同加固方式对安全系数的影响；

4）比较不平衡推力传递法、极限分析上限法和强度折减法3种计算方法安全系数计算结果，安全系数相近。