循环加载下压实黄土的边界面塑性本构模型

代倩 廖红建 康孝森 孙玉军 周恒

收稿日期：2023-10-15

基金項目：陕西省教育厅科研计划项目（22JK0445）；陕西省秦创原“科学家+工程师”队伍建设项目（2023KXJ-178）。

第一作者：代倩，女，博士生，从事黄土动力学试验与数值模拟等研究，daiqian68@stu.xjtu.edu.cn。

通信作者：廖红建，女，博士，教授，从事岩土本构关系、岩土工程减灾与防灾等研究，hjliao@mail.xjtu.edu.cn。

摘要  压实黄土的动应力应变关系预测是黄土高原平山填方工程长期运营涉及的关键问题之一，已有模型预测压实黄土的动本构关系难度较大。该文在边界面塑性框架下，引入动态映射法则，提出了一个反映应变累积的循环加载塑性模量表达式，构建了循环加载条件下压实黄土边界面塑性本构模型，分析了循环应力比与围压对应力应变关系与模量的影响规律，采用压实粉质黄土动三轴试验结果进行了验证。结果表明，该循环加载塑性模量基本反映了压实黄土的应变累积行为，所构建的本构模型考虑了循环应力比对动应力应变关系与模量的影响，可为填方压实黄土长期变形分析提供参考。

关键词  压实黄土;循环加载;应力应变;本构模型;塑性模量

中图分类号： TU473  DOI：10.16152/j.cnki.xdxbzr.2024-01-004

Bounding surface plasticity model of compactedloess under cyclic loading

DAI Qian1，2，  LIAO Hongjian1，2， KANG Xiaosen3， SUN Yujun4， ZHOU Heng5

（1.School of Human Settlements and  Civil Engineering， Xian Jiaotong University， Xian 710049， China;

2.School of Civil Engineering，   Xian Jiaotong University City College， Xian 710018， China;

3.School of Geological Engineering and Geomatics， Changan University， Xian 710064， China;

4.State Power Investment Corporation， Yellow River Upper Reaches Hydropower Development Co.， Ltd.， Xining 810001，  China；

5.Powerchina Northwest Engineering Co.， Ltd.， Xian 710065， China）

Abstract  The prediction of the dynamic stress-strain relationship of compacted loess is essential in the projects of gully reclamation for farming and cutting mountains for city building in Loess Plateau. It is still difficult to predict the behaviors. To fill the gap， this paper formulates a bounding surface plasticity model for compacted loess subjected to cyclic loading. Specifically， a plastic modulus for cyclic loading is proposed to reflect the behaviors of  accumulated strain， and an updated mapping rule is introduced. Furthermore， the influence of confining pressure and cyclic stress ratio on stress-strain relationship and modulus is shown by several case studies， which is verified by experimental tests of compacted loess. The results show that the plastic modulus reflects  accumulated strain of compacted loess.The constitutive model considers the effect of cyclic stress ratio on dynamic stress-strain relationship and modulus of compacted loess because of the proposed plastic modulus and updated mapping rule. The results can give reference for analysis of long-term deformation of loess-filled foundation.

Keywords  compacted loess; cyclic loading; stress-strain; constitutive model; plastic modulus

黄土地区平山造城、 治沟造地、 高速铁路等工程涉及不同规模的填方压实黄土（见图1）， 长期循环荷载下压实黄土产生累积变形，准确预测压实黄土的循环加载累积变形对于陕西、 山西及甘肃等地区的黄土填方工程运营具有重要的实际意义。

目前，循环加载条件下砂土与黏土本构模型研究较为广泛和深入。砂土模型一般采用锥面屈服面，基于记忆面［1］或边界面等［2］构建砂土循环加载本构模型［3-4］，考虑相变状态参量［5］、组构演化［6］及非共轴特性［7］等。黏土循环加载本构模型一般采用修正剑桥模型屈服面，基于边界面塑性，采用映射法则与塑性模量反映循环加载过程中的塑性应变累积［8-9］，求解复杂动力边值问题［10］。还将非饱和土水力特性引入边界面塑性框架，建立了热水力耦合模型［11］，以及考虑非饱和状态参量和颗粒破碎参数［12］及损伤特性［13］。而黄土循环加载本构模拟研究较少，已有研究主要是单调加载下黄土的损伤特性［14-15］、各向异性［16］、结构性［17-18］、临界状态线不唯一［19］等。可借鉴以往黏土本构模型构建黄土的循环加载本构模型，崔广芹在边界面塑性框架下研究了黄土的动本构模型［20］。在土的动本构模型中，映射中心与塑性模量关系到加载过程中塑性应变累积，映射中心可能沿应力加载方向运动［21］。塑性模量影响循环加载条件下黄土偏应变累积稳定与非稳定状态，合适的循环加载塑性模量对预测压实黄土动力特性至关重要［10，22］。

虽然上述学者开展了黄土动本构模型的研究，但模型尚未考虑到黄土的临界状态线不唯一的基本特性，尤其是粉质黄土中粉粒组含量高，属于间隔级配土一类，且大孔隙架空结构导致其初始孔隙比范围较大，临界状态线明显依赖于初始孔隙比［19，23］。而临界状态线对于循环加载下黄土的动力行为预测至关重要，循环加载下黄土的本构关系预测仍然是一个挑战。本文在边界面塑性理论框架下，基于Kang等建立的边界面塑性本构模型［24］，引入动态映射法则，提出一个循环加载条件下压实黄土塑性模量表达式，推导压实黄土动本构模型，模拟不同循环应力比时压实黄土动本构关系。研究结果可为填方黄土变形分析提供参考。

1  本构模型

1.1  考虑黄土临界压力比的边界面

传统各向异性边界面不能反映黄土的临界状态线不唯一性［19，23］，可通过临界压力比这一指标反映（见图1），故采用考虑临界压力比的边界面［24］，

[AKf-]=（[AKq-D]-[AKp-D]′α）2+[AKM-]2[AKp-D]′（[AKp-D]′-[AKp-D]′0）=0  [JY]（1）

式中：（[AKp-D]′，[AKq-D]）为各向异性结构性边界面上的像应力;α为各向异性不变量;p′[TX-]0为等向硬化参数;[AKM-]由下式确定。

[AKM-]=（+（1-）[AKp-D]′[AKp-D]′0-1）[KF（]M2-α2[KF）]  [JY]（2）

式中：M為不同洛德角时临界状态线斜率，M=gθMc;由下式确定［24］。

=[KF（][SX（]M-αc[]M+αc[SX）][KF）][SX（]r[]（r-1）32[SX）]-[SX（]1[]r-1[SX）]  [JY]（3）

式中：αc为临界状态时α的值，临界压力比r反映临界状态线与等向压缩线的距离。

1.2  加载面与塑性势面

对于超固结土，初始时加载面在边界面内，破坏时加载面与边界面一致，加载面为［24］

[AKf-]=（q-p′α）2+[AKM-]2p′（p′-p′0）=0  [JY]（4）

式中：（p′，q）为当前应力，位于加载面上。循环加载过程加载面与边界面相似，相似中心为反转应力点。

塑性势函数［24］

g=（[AKq-D]-[AKp-D]′α）2+M2[AKp-D]′（[AKp-D]′-[AKp-D]′g）  [JY]（5）

式中：[AKp-D]′g反映塑性势面大小。

1.3  等向硬化与旋转硬化

等向硬化采用修正剑桥模型硬化法则，

d[AKp-D]′0=〈L〉[SX（][AKp-D]′0[]Cp[SX）][SX（]g[][AKp-D]′[SX）]  [JY]（6）

式中：Cp为λ-κ1+e0，λ与κ分别为压缩线与等向加卸载线的斜率。

初始各向异性与诱发各向异性采用Dafalias与Taiebat提出的各向异性演化表达式［25］，

dα=〈L〉crpa（αb-α）[SX（][AKp-D]′[][AKp-D]′0[SX）]  [JY]（7）

式中： pa为标准大气压; cr为常数， 控制各向异性结构性边界面q轴方向的旋转率。 〈·〉为Maca-uley算子。αb为各向异性不变量α的上限值，表达式为［25］

αb=±[SX（]M[]ζ[SX）]（1-eζ|η|M）  [JY]（8）

式中：ζ为控制参数。

1.4  循环加载映射法则

边界面塑性框架下，预测循环加载条件下应变累积，需采用更新映射中心法则［26］，循环加载条件下，映射中心从上一个应力反转点更新至下一个应力反转点（见图2）。压实黄土首次加载与后续循环加卸载所产生的累积应变规律不同，首次加载时累积应变显著大于后续循环加载一次时应变累积。

首次加载时映射中心设为原点，单调加载本构模型亦设原点为映射中心，后续循环加载时映射中心设定为应力反转点，已广泛应用于循环加载本构模型中。采用Seidalinov与Taiebat所提出的更新映射法则［27］如下，

[AKp-D]′=p′mc+ρ（p′-p′mc）

[AKq-D]=qmc+ρ（q-qmc）[JY]（9）

式中：ρ为相似比;（p′mc，qmc）为映射中心的应力状态。将像应力代入边界面表达式中即可求得相似比ρ，算得当前应力与像应力在应力空间的距离，确定循环加卸载中塑性模量值。

1.5  循环加载塑性模量

塑性模量是边界面塑性理论最为重要的一部分，直接关系到塑性变形累积计算的准确性。在边界面塑性框架下，塑性模量Kbδ=Kb+Kδ。Kb为各向异性结构性边界面上像应力相关的塑性模量分量，由各向异性结构性边界面一致性条件确定，而经典塑性理论只有Kb这一项，只能反映应力状态达到屈服面时塑性应变，不能反映压实黄土初始塑性应变累积与循环加载塑性应变累积效应。Kδ为当前应力状态相关的塑性模量分量，由当前应力与像应力在应力空间中坐标决定。

基于Seidalinov与Taiebat［26］的塑性模量公式，考虑循环加载下压实黄土变形规律，提出一个改进循环加载塑性模量Kδ，

Kδ=[AKp-D]′04（ρ-1）2e-ad∫[SX（]1[]ε0[SX）]|Δεpq |  [JY]（10）

式中：ad为塑性模量衰减参数;ε0为参考应变值0.15;Δεpq为塑性偏应变增量。

循环加载条件下，当ad越大，Kδ衰减越快，反映随着塑性应变累积过程中压实黄土更容易破坏。

（ρ-1）2反映当前应力状态相关的塑性模量Kb大小与当前应力和像应力在应力空间中的距离密切相关。若当前应力远离像应力，如当前应力接近映射中心，则（ρ-1）2达到较大值，则Kδ较大，塑性应变累积极小，接近弹性状态。若当前应力逐渐接近像应力，例如当前应力在映射中心与像应力中间时，则（ρ-1）2逐渐接近0，Kδ逐渐接近0，塑性应变累积率逐渐增大，表现为材料由弹性状态向弹塑性状态过渡。当前应力与像应力相等时，则（ρ-1）2为0，Kδ为0，塑性应变累积率达到最大，表现为材料弹塑性状态，这一状态与经典塑性力学弹塑性状态一致。

由边界面式（1）的一致性条件，推导得塑性模量Kb表达式为

Kb=cpa（α-αb）[SX（][AKp-D]′[][AKp-D]′0[SX）][SX（][AKf-][]α[SX）]-[SX（][AKp-D]′0[]Cp[SX）][SX（]g[][AKp-D]′[SX）][SX（][AKf-][][AKp-D]′0[SX）]  [JY]（11）

1.6  应力应变关系

根据非关联流动法则，

dεp=〈L〉[SX（]g[][AKσ-D][SX）]  [JY]（12）

式中：塑性乘子表达为

L=[SX（]1[]Kbδ[SX）][JB（（][SX（]f[][AKσ-D][SX）]：d[AKσ-D][JB））]  [JY]（13）

根据广义胡克定律，

dσ=Dedεe  [JY]（14）

式中：为De弹性矩阵。

由应变可加性计算总应变增量，

dε=dεe+dεp  [JY]（15）

由上述表达式及一致性条件，得增量型应力应变关系为

dσ=Depdεe  [JY]（16）

式中：弹塑性刚度矩阵为

Dep=De-（Kbδ+nDem）-1DemnDe [JY]（17）

式中：m和n分别为

m=（g／[AKσ-D]）／‖g／[AKσ-D]‖  [JY]（18）

n=（[AKf-]／[AKσ-D]）／‖[AKf-]／[AKσ-D]‖  [JY]（19）

2  算例分析

2.1  模型参数

模型含10个材料参数，通过常规三轴试验、循环加载试验及试算确定。①强度参数：黏聚力c，斜率Mc为常规三轴压缩路径下临界状态线的斜率，Me为常规三轴拉伸路径下临界状态线的斜率，通过常规三轴试验即可确定。②压缩参数与回弹参数：λ和κ分别为v-ln p′平面上等向压缩线斜率与卸载加载线斜率，通过等向压缩试验确定。③弹性参数：泊松比μ设为0.3。④临界压力比：r反映的是临界状态时有效平均主应力p′与硬化参数p′0之间的关系，在v-ln p′平面上分析临界状态线与等向压缩线确定（见图1）。⑤旋转硬化参数：cr控制边界面旋转，ζ反映了应力路径对旋转硬化参数上限值的影响，通过试算确定［25］。⑥塑性模量参数：ad控制塑性模量增大或减小，根据循环加卸载试验应变累积确定，若偏应变稳定于某一值且小于破坏应变，则ad取正值;若偏应变大于破坏应变且不稳定，则ad取负值。

2.2  算例

通过循环加载算例分析不同循环应力比条件下应力应变滞回圈、循环加载非线性、动杨氏模量的变化规律。材料参数值根据一般土性参数设定（见表1），结果见图3。

由圖3（a）可知，循环加载过程中应力应变曲线非线性，应力应变滞回圈逐渐趋于稳定，循环应力比越大，滞回圈越显著，反映了循环加载下黄土的弹塑性行为。进一步，随着循环次数的增加，累积塑性应变增大，但变化量越来越小，尤其是循环应力比CSR（σd／（2σc））越大，塑性应变累积越快。

由图3（b）可知，循环加载过程中动杨氏模量逐步衰减，当循环应力比为常数，动杨氏模量随着塑性应变累积而减小，当累积塑性应变为某一特定值，动杨氏模量随着循环应力比增大而减小。该规律反映了循环加载过程中土结构损伤演化与应变累积和循环应力比的相关性，循环应力比较小引起结构损伤较小，循环应力比较大引起结构损伤较大，符合循环加载下黄土变形规律。

3  驗证与讨论

应用该模型预测循环加载条件下饱和压实黄土的动应力应变关系、塑性应变累积及动杨氏模量衰减规律［27］。材料参数取值根据文献［24］确定（见表2）。

由图4、5可知，模型模拟了饱和压实黄土的循环加载非线性及应力应变滞回效应。首先，当循环应力比较大时，饱和黄土应力状态接近边界面，应力应变表现出强非线性，轴向应变累积显著，且首次加载应力应变曲线与后续加载应力应变曲线显著不同。模型通过引入更新映射中心法则，首次加载时映射中心为原点，后续加载时映射中心为应力反转点，较好模拟了饱和压实黄土首次加载与后续加载应力应变关系。其次，饱和压实黄土应力应变滞回效应显著，循环应力比越大滞回圈愈大，且随着加载次数增大逐渐趋于稳定，模型较好地模拟了应力应变滞回圈疏密变化，经典弹塑性模型难以实现。

由图6可知，模型基本预测了饱和压实黄土的塑性应变累积行为。随着循环次数的增大，累积轴向应变增大，轴向应变增加速率逐渐减小。循环应力比越大，累积轴向应变越大，土样更容易达到破坏条件，如CSR=0.43对应的轴向应变远大于CSR=0.35对应的轴向应变（见图6）。一方面，循环应力比越大，应力状态越靠近边界面，导致塑性模量较小且应变增量较大，更易产生塑性应变累积。另一方面，循环应力比越大，应力状态更快到达临界状态线，更快达到破坏条件。

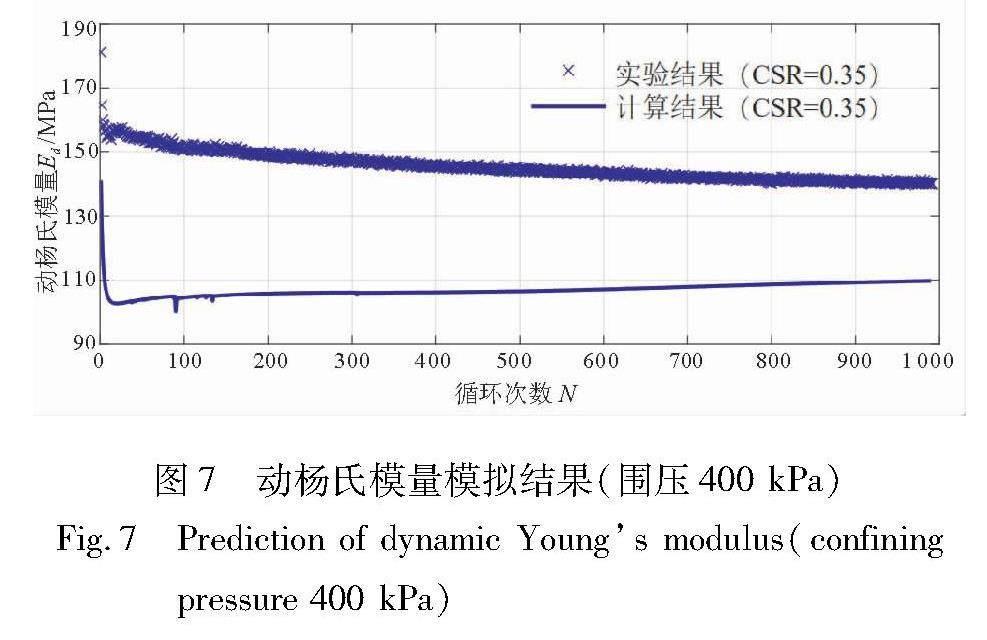
由图7可知，模型基本预测了饱和压实黄土动杨氏模量衰减规律。动杨氏模量计算值小于动杨氏模量实验值，但趋势一致，且在一个数量级。动杨氏模量随着围压的增大而增大，反映了围压对模量的影响。随着循环加载次数的增大，动杨氏模量衰减，在102次循环次数内衰减显著，反映了循环加载下黄土结构劣化规律。

4  结语

为预测压实黄土的动本构关系，本文修正了既有边界面塑性本构模型，预测分析了饱和压实粉质黄土动三轴试验结果，得出以下主要结论。

在边界面塑性理论框架下，引入了一个动态映射法则，提出了一个反映应变累积的循环加载塑性模量表达式，构建了循环加载下压实黄土边界面塑性本构模型，分析了循环应力比对应力应变关系与动杨氏模量的影响规律。

采用该模型预测分析了循环加载下饱和压实黄土动本构关系，模型计算结果与试验结果分析表明所提出的循环加载塑性模量能够反映压实黄土的循环加载非线性、塑性应变累积、应力应变滞回及动杨氏模量衰减规律。研究方法与结果可为填方压实黄土长期变形分析提供参考。

参考文献

［1］CORTI R， DIAMBRA A， WOOD D M， et al. Memory surface hardening model for granular soils under repeated loading conditions［J］. Journal of Engineering Mechanics， 2016， 142（12）：04016102.

［2］WANG Z L， DAFALIAS Y F， SHEN C K. Bounding surface hypoplasticity model for sand［J］.Journal of Engineering Mechanics， 1990， 116（5）：983-1001.

［3］方火浪， 沈扬， 郑浩，等. 砂土三维多重机构边界面模型［J］.岩土工程学报， 2017， 39 （7）： 1189-1195.

FANG H L， SHEN Y， ZHENG H， et al. Three-dimensional multi-mechanism bounding surface model for sands［J］.Chinese Journal of Geotechnical Engineering， 2017， 39 （7）： 1189-1195.

［4］董建勋， 刘海笑， 李洲. 适用于砂土循环加载分析的边界面塑性模型［J］. 岩土力学， 2019， 40（2）： 684-692.

DONG J X， LIU H X， LI Z. A bounding surface plasticity model of sand for cyclic loading analysis［J］. Rock and Soil Mechanics， 2019， 40（2）： 684-692.

［5］迟明杰， 赵成刚， 李小军. 剪胀性砂土边界面模型的研究［J］. 工程地质学报， 2008， 16（3）： 128-134.

CHI M J， ZHAO C G， LI X J. A bounding surface plasticity based constitutive model for dilatant sand ［J］. Journal of Engineering Geology， 2008， 16（3）： 128-134.

［6］WOO S I， SALGADO R. Bounding surface modeling of sand with consideration of fabric and its evolution during monotonic shearing［J］. International Journal of Solids and Structures， 2015， 63：277-288.

［7］FANG H L， ZHENG H， ZHENG J. Micromechanics-based multimechanism bounding surface model for sands［J］. International Journal of Plasticity， 2017， 90：242-266.

［8］XIAO Y， LIU H L， LIU H， et al. Unified plastic modulus in the bounding surface plasticity model［J］. Science China Technological Sciences， 2016， 59（6）：932-940.

［9］HU C， LIU H X， HUANG W. Anisotropic bounding-surface plasticity model for the cyclic shakedown and degradation of saturated clay［J］. Computers and Geotechnics， 2012， 44： 34-47.

［10］KIM T， JUNG Y H. A new perspective on bounding surface plasticity： The moving projection origin［J］. KSCE Journal of Civil Engineering， 2017， 21（3）：652-658.

［11］ZHOU C， NG C W W. Simulating the cyclic behaviour of unsaturated soil at various temperatures using a bounding surface model［J］. Géotechnique， 2016， 66（4）：344-350.

［12］RUSSELL A R， KHALILI N. A unified bounding surface plasticity model for unsaturated soils［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2006， 30（3）：181-212.

［13］YANG C， CUI Y J， PEREIRA J M， et al. A constitutive model for unsaturated cemented soils under cyclic loading［J］. Computers and Geotechnics， 2008， 35（6）：853-859.

［14］FU Y K， GAO Z W， HONG Y， et al. Destructuration of saturated natural loess： From experiments to constitutive modeling［J］. International Journal of Damage Mechanics， 2021， 30（4）：575-594.

［15］褚峰， 張宏刚， 邵生俊. 陇东Q3结构性黄土压剪损伤本构模型试验研究［J］.岩土力学， 2019， 40（10）： 3855-3870.

CHU F， ZHANG H G， SHAO S J. Experimental study of constitutive model of Longdong Q3 structural loess with compressive and shearing damage ［J］. Rock and Soil Mechanics， 2019， 40（10）： 3855-3870.

［16］侯乐乐， 翁效林， 崔艺铖， 等.  K0固结结构性黄土的各向异性本构模型［J］.岩石力学与工程学报， 2022， 41（10）： 2124-2134.

HOU L L， WENG X L， CUI Y C， et al. Critical state constitutive model of K0 consolidated structural loess［J］.Chinese Journal of Rock Mechanics and Engineering， 2022， 41（10）： 2124-2134.

［17］姚志华， 陈正汉， 方祥位， 等. 非饱和原状黄土弹塑性损伤流固耦合模型及其初步应用［J］.岩土力学， 2019， 40（1）： 216-226.

YAO Z H， CHEN Z H， FANG X W， et al. Elastoplastic damage seepage-consolidation coupled model of unsaturated intact loess and its application ［J］. Rock and Soil Mechanics， 2019， 40（1）： 216-226.

［18］蒋明镜. 现代土力学研究的新视野： 宏微观土力学［J］.岩土工程学报， 2019， 41（2）： 195-254.

JIANG M J. New paradigm for modern soil mechanics：Geomechanics from micro to macro ［J］. Chinese Journal of Geotechnical Engineering， 2019， 41（2）： 195-254.

［19］康孝森， 廖红建， 黄强兵， 等. 结构性黄土的临界压力比及其边界面塑性本构模型预测［J］.岩土力学， 2022， 43（6）： 1469-1480.

KANG X S， LIAO H J， HUANG Q B， et al. Spacing ratio of structural loess and its prediction using bounding surface plasticity model ［J］. Rock and Soil Mechanics， 2022， 43（6）： 1469-1480.

［20］崔广芹. 饱和黄土动力本构模型及地铁隧道周围土层变形分析［D］. 西安：西安建筑科技大学， 2014.

［21］JUNG Y H， LEE J H. Experimental validation of the radial mapping rule in bounding surface plasticity model［J］. Journal of the Korean Geotechnical Society， 2013， 29（1）： 171-181.

［22］KAN M E， TAIEBAT H A， KHALILI N. Simplified mapping rule for bounding surface simulation of complex loading paths in granular materials［J］. International Journal of Geomechanics， 2014， 14（2）：239-253.

［23］XU L， COOP M R. The mechanics of a saturated silty loess with a transitional mode［J］. Géotechnique， 2017， 67（7）： 581-596.

［24］KANG X S， LIAO H J， HUANG Q B， et al. Enhanced anisotropic bounding surface plasticity model considering modified spacing ratio of anisotropically consolidated clay［J］. Acta Geotechnica， 2022， 17（6）： 2213-2233.

［25］DAFALIAS Y F， TAIEBAT M. Anatomy of rotational hardening in clay plasticity［J］. Géotechnique， 2013， 63（16）： 1406-1418.

［26］SEIDALINOV G， TAIEBAT M. Bounding surface SANICLAY plasticity model for cyclic clay behavior［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2014， 38（7）：702-724.

［27］代倩， 廖紅建， 康孝森， 等. 动荷载下填方体压实黄土动应变与动孔压变化规律研究［J］.岩土工程学报， 2021， 43（S1）： 235-240.

DAI Q， LIAO H J， KANG X S， et al. Behaviors of dynamic strain and pore pressure of compacted loess in loess-filled foundation induced by dynamic loading［J］. Chinese Journal of Geotechnical Engineering， 2021， 43（S1）： 235-240.

（编  辑  张  欢）