核心素养导向下的数学教学设计

武旦珠

核心素养导向下的数学教学是对传统教学的一次变革，摆脱了过去以课时为单位的传统范式，推崇以单元为整体的设计理念。这种变革体现了对数学知识内在逻辑关系的深层次思考，教学设计应该体现单元整合教学内容。这种教学设计旨在通过深入挖掘数学知识之间的关系，为学生提供更为系统和全面的学习体验。

教学设计要充分考虑核心素养的重要性，确保在整个教学过程中的指导作用。教学目标应该是全面的、有层次的，可以涵盖知识、技能和态度的培养，以确保学生在学习过程中获得全面的发展。教师要考虑学生的数学核心素养、创造力、批判性思维等方面的发展。在每个课时中，结合教学内容和目标展开教学，能够更好地发展学生的核心素养。

【教材分析】

北师大版数学八年级上册“直角三角形三边的关系”，是“勾股定理”章节的主要内容，重点讲解了勾股定理的证明过程。教材通过两个例子“正方形的瓷砖”和“试一试”来发现直角三角形三边之间的关系。接着，通过“做一做”的实践验证，学生先获得直接的经验，再进行总结和归纳，证明勾股定理。

勾股定理是几何学中最为重要的定理之一，它揭示了直角三角形中三边的数量关系。直角三角形中斜边较长，而另外两条边较短，该定理证明它们之间有着精确的数量关系，为学生今后学习解直角三角形问题奠定基础。因此，探索直角三角形三边的关系对学生来说非常重要，既能使学生更好地理解直角三角形，又能培养他们的逻辑思维能力。

【学情分析】

八年级学生已经具备了一定的逻辑思维和抽象思维能力，并且掌握了学习数学的基本方法。直角三角形是他们非常熟悉的图形，因此，通过自主探索、合作互助、交流分享的方式来验证和应用勾股定理是非常适合的。通过这样的学习方式，学生能够轻松、愉快地完成本节课的学习目标。

【教学目标】

1.育人目标

（1）通过探究、验证、证明和应用勾股定理，培养学生对数学学习的意识和能力。通过自主探索、合作交流的学習方式，培养学生独立思考、分析和解决问题的能力。

（2）通过勾股定理的证明，让学生知道勾股定理是中国古代数学的杰出成果之一，还被广泛应用于日常生活和工程技术中。通过学习勾股定理，学生将不仅仅掌握数学知识，还能够认识到中国传统数学在世界数学发展史上的地位和作用，激发学生热爱祖国和中华优秀传统文化的情感。

2.学科素养目标

（1）通过对勾股定理的学习，引导学生深刻感受到数学在人类文明进程中的重要性，了解中国传统数学在世界数学发展史上的地位和影响力，激发学生对祖国的热爱。

（2）通过勾股定理的探索和应用，培养创新思维的种子。他们将学会从不同的角度思考问题，寻找创新的解决方法，为将来的学习和生活奠定坚实的基础。通过这些努力，学生将更加热爱祖国的传统文化，为祖国未来的发展做出积极贡献。

【教学重点】

1.经历勾股定理的探索过程，亲身体验到数学知识的发现和证明过程。

2.掌握勾股定理原理，并能够灵活运用该定理解决一些简单的实际问题。

【教学难点】

勾股定理的探究和解决相关的实际问题。

【内容与中考分析】

本节的内容是探究、验证、证明和应用勾股定理。勾股定理是各类考试命题中的热门内容，通常会结合其他知识进行综合考查，其所占比例不少于10%，这体现了勾股定理在数学教学中的重要性。因此，学生需要充分掌握勾股定理的原理，并能够熟练应用于解决相关问题，以应对中考。

【教学过程】

一、创设情境，引入新课（5分钟）

通过展示一些直角三角形的实际应用场景（如建筑、地理测量等），引起学生对直角三角形的兴趣和重新认识，了解学生对直角三角形的认识程度。

1.一般三角形三条边之间存在怎样的数量关系？

2.直角三角形的三条边除一般关系外，还存在特殊的数量关系吗？

教师提出问题，学生独立思考，小组合作交流后，代表在全班分享交流。

教师出示学习目标：

1.掌握勾股定理的内容和证明，能够灵活运用勾股定理进行计算。

2.通过动手操作、观察分析、合作交流提升逻辑推理的能力。

二、实验探究，生成新知（15分钟）

【探究1】直角三角形三条边之间的数量关系

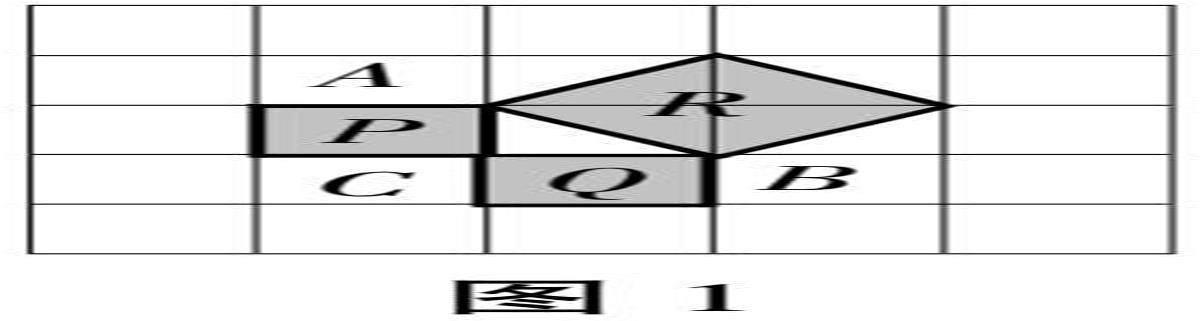
学生自学：图1是正方形瓷砖铺成的地面，标记了的着色正方形P、Q、R。那么，这三个正方形的面积之间是否存在特殊的关系呢？

问题1：观察图形，直接写出三个正方形的面积，提示学生从数和形两个角度思考，渗透数形结合的思想。

正方形P的面积为：SP=AC2=1

正方形Q的面积为SQ=BC2=1

正方形R的面积为SR=AB2=2

问题2：你能发现图1中正方形P、Q、R的面积之间有什么关系吗？

SP+SQ=SR

问题3：直角三角形三条边长之间的关系如何呢？

让学生在充分的思考和小组讨论的情况下发言：

AC2+BC2=AB2

学生活动：先观察课本图1，在探索记录的过程中，要注意数形结合，思考直角三角形三边的关系。

教师活动：（1）明了学情：观察学生在探究、验证结论的过程中所用的思路和方法以及过程的合理性和严密性，教师有针对性地进行引导。

（2）差异化指导：在学生进行探究时，教师积极参与、巡视、随时发现问题并进行引导和点拨，帮助他们更好地理解问题。

【探究2】引导学生观察直角三角形的特点，介绍勾股定理的概念，探究：

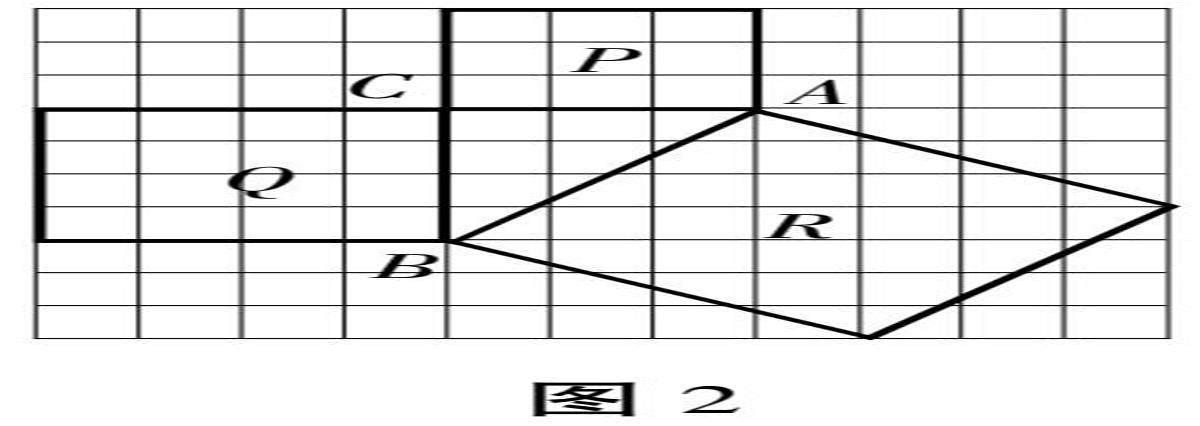
1.图2是利用更多的正方形地砖铺成的地面，类比探究1，学生自主探究“直角三角形三边长度之间关系”（过程写在学案上）。

（由特殊的等腰直角三角形到一般的直角三角形，体现了由特殊到一般的数学思想和方法，教师必要时给学生提醒）

分析：大正方形R的面积可以用“切割法”或“切补法”来计算。

∵Sp=AC2=9 SQ=BC2=16 SR=AB2=25

∴AC2+BC2=AB2

2.完成课本109页“做一做”，让学生动手操作，能按照要求画出图形，独立完成并验证：“直角三角形中，两直角边的平方和等于斜边的平方。”（把图画在学案上，小组内交流讨论后展示和分享）

学生在独立思考和小组讨论的过程中，可以用不同的方法验证勾股定理，尝试给出勾股定理的证明过程，掌握一种证明勾股定理的方法，并能正确书写逻辑推理过程，从而加深对勾股定理的理解。

【探究3】学生自学：（1）根据课本第110页的“读一读”内容，了解三国时期的数学家赵爽深入研究《周髀算经》，利用“弦图”证明了勾股定理，它标志着中国古代的数学成就，培育学生热爱数学、热爱祖国的情怀。

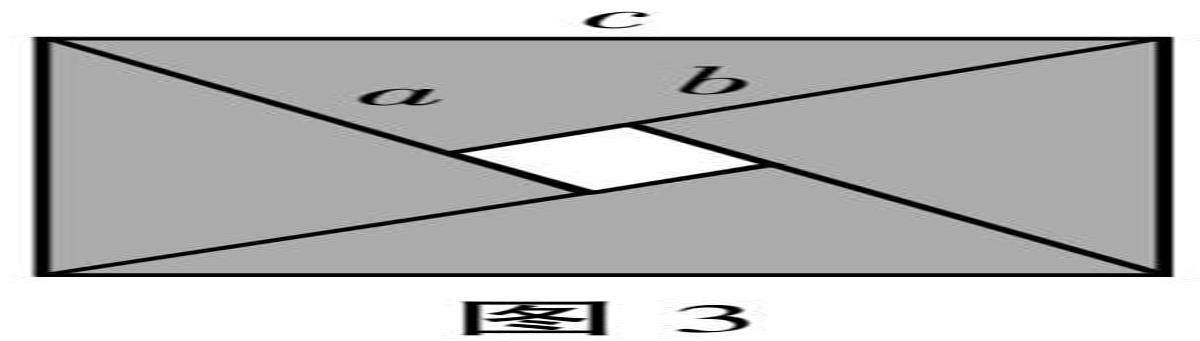
【证明勾股定理】图3是弦图的示意图，它是一个小正方形和四个全等的直角三角形拼成一个大正方形，试证明：a2+b2=c2。

学生先尝试证明，教师可以提示：

图形是拼凑而成的，既没有重叠，也没有空隙，所以面积不会变，因此用“等积法”证明。

（2）大正方形的面积=4个全等的直角三角形面积+小正方形面积。

4×ab+（b-a）2=c2，化简得a2+b2=c2。

（3）学生归纳总结，教师点评和概括：

对于任意的直角三角形，如果a、b为两条直角边的长，c为斜边的长，那么a2+b2=c2。

勾股定理：直角三角形两直角边的平方和等于斜边的平方。

定理变形：在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c，则

c2=a2+b2

a2=c2-b2

b2=c2-a2

学生活动：独立尝试用符号语言、文字语言两种形式表达勾股定理的内容。

教师活动：关注学生在证明定理过程中对勾股定理的理解和运用情况，以便及时引导与点拨。

三、应用定理，巩固新知（20分钟）

教师采取学生板书和学案相结合的方法，完成后组内互评，教师点评。

1.在Rt△ABC中，已知∠B=90°，AB=7，BC=24，求AC。

分析：可以直接用公式计算，也可以用数形结合法。这里特别强调∠B=90°，防止定式思维的干扰。

分析：在Rt△ABC中

∵∠B=90°，AB=7，BC=24

根据勾股定理，得AC2=AB2+BC2

∴AC=25

2.在Rt△ABC中，∠C=90°，斜边为c

①已知a=5，b=12，求c。②已知b=2，c=3，求a。

师生之共同分析后，教师示范①，学生板书②。（要求规范推理过程）

解：①在Rt△ABC中，

∵∠C=90°，a=5，b=12，

根據勾股定理，得a2+b2=c2。

∴c=13

②学生板书（要求规范推理过程），完成后师生共同进行评价。教师用课件展示解题过程，让学生对照自己的解题过程，特别强调几何语言的表达及其逻辑推理的准确性。

3.在操场上有两棵古树，但是不能直接测量它们之间的距离，请同学们利用勾股定理的知识，设计一个直角三角形，通过测量相关数据，计算出两棵树间的距离，把你的设计方案与同学们分享。

这是一道开放性题目，学生可以充分发挥自己的聪明才智，张开思维的翅膀，在独立思考的基础上生生互动、师生互动，各自发表不同的见解，提出不同的设计方案进行研讨。

四、课堂小结，升华新知（5分钟）

1.这节课，我的收获是？（问自己）

2.这节课，你最感兴趣的地方是？（问同桌）

3.我们能进一步研究的问题是？（问同桌）

五、作业设计与布置，内化新知

1.基础性作业（全体学生）

（1）课本117页，习题14.1，第1、2题。

（2）阅读教材118～119页“阅读材料”的内容，体验勾股定理之美，丰富学生的学习体验。

2.拓展性作业（有余力的学生）：一个长方体的粉笔盒，它的长是10 cm、宽是6 cm、高是8 cm，一只蚂蚁在粉笔盒的顶点P处，它想吃到与P相对的顶点Q处的蜂蜜，但只能沿着粉笔盒表面爬行，你知道蚂蚁是怎样爬行的吗？请你求出它爬行的最短距离。

3.推荐性作业（有兴趣的学生）：为了更好地理解勾股定理，建议有兴趣的同学撰写一篇以勾股定理为主题的小论文。

（设计意图：按照“双减”政策的要求，教师分层布置作业，以满足不同学生的学习需求和发展，逐渐提升学生的解题能力。）

（作者单位：甘肃省秦安县兴国镇初级中学）

编辑：陈鲜艳